Содержание

1. Теоретическая часть. 3

Подбор формы кривой  прогнозирующей функции методом исследования характеристик прироста. 3

1.1.  Основные  модели прогнозирующей функции. 3

1.2. Этапы построения моделей. 5

1.3. Модель авторегрессии. 7

1.4. Модель скользящего среднего. 8

1.5. Модель Бокса-Дженкинса (АРИСС) 10

2. Практическая часть. 13

Список литературы.. 16

1. Теоретическая часть

Подбор формы кривой  прогнозирующей функции методом исследования характеристик прироста

1.1.  Основные  модели прогнозирующей функции

Идея использования математических моделей для описания поведения физических объектов является общепризнанной. В частности, иногда удается получить модель, основанную на физических законах, что дает возможность вычислить почти точное значение какой-либо зависящей от времени величины в любой момент времени. Например, мы можем вычислить траекторию ракеты, запущенной в известном направлении с известной скоростью. Такие модели называются детерминированными, хотя реальные объекты крайне редко бывают целиком детерминированными (например, неучтенная скорость ветра может слегка отклонить ракету от курса). Поэтому в случае экологических объектов, для которых доля влияния случайных (неучитываемых) факторов традиционно очень велика, можно предложить модели, позволяющие вычислить лишь вероятность того, что некоторое будущее значение будет лежать в определенном интервале. Такие модели называются вероятностными, либо стохастическими. Интервал времени, на который существует необходимость прогноза вперед при решении конкретной проблемы, называется периодом упреждения.

Пусть x(t + l) - измеренное значение экологического показателя в момент времени t с упреждением на будущее l. Функция j _t(l), l = 1, 2, ..., дающая в момент t прогнозы для всех будущих времен упреждения, будет называться прогнозирующей функцией в момент t. Очевидна цель - получить такую прогнозирующую функцию, у которой среднее значение квадрата отклонения истинного значения от прогнозируемого [x(t + l) - j _t(l)]² является наименьшим для каждого упреждения l. В дополнение к вычислению наилучшего прогноза необходимо также указать его точность, чтобы можно было оценить риск, связанный с решениями, основанными на прогнозировании. Точность прогноза выражается, как правило, доверительными пределами по обе стороны от прогнозируемых значений для любого удобного значения уровня вероятности h (например, для 95%).

Как было отмечено выше, простые параметрические модели тренда не всегда обеспечивают эффективное вычисление будущего поведения объектов. Определенной альтернативой являются итеративные модели, основанные на концепции того, что временные ряды, в которых наблюдается отчетливая автокорреляция, целесообразно рассматривать как результат некоторого преобразования последовательности независимых импульсов a_t. Эти импульсы - реализация случайных величин с фиксированным распределением, которое обычно предполагается нормальным с нулевым средним и дисперсией s _a², что соответствует "белому шуму". Считается, что "белый шум" a_t можно трансформировать в традиционно рассматриваемый стационарный процесс, используя следующие преобразования:

·                    фильтр авторегрессии (АР), в котором текущее значение процесса y_t выражается в виде конечной линейной совокупности предыдущих значений процесса y_t-1, y_t-2, ... плюс случайный импульс a_t;

·                    фильтр скользящего среднего (СС), в котором процесс y_t образуется из белого шума a_t как взвешенная сумма предыдущей последовательности импульсов a_t, a_{t -1}, a_{t -2} ...

Современная статистическая теория оценивания параметров таких моделей, заложенная еще советскими математиками.  Модели АР и СС достаточно высокого порядка могут хорошо аппроксимировать почти любой стационарный процесс. В связи с этим модель АР часто применяется для моделирования остатков в той или иной параметрической модели, например регрессионной модели или модели тренда. Для достижения большей гибкости в подгонке модели к наблюдаемым временным рядам часто целесообразно объединить в одной модели оба преобразования, получив комбинированную модель авторегрессии - скользящего среднего (АРСС). Уравнения АР и СС могут быть вычислены и для нестационарных процессов (особенно, если нестационарность носит однородный характер). Однако более эффективна для описания как стационарных, так и нестационарных рядов со стационарными приращениями d-го порядка и рациональным спектром комбинированная модель авторегрессии - интегрированного скользящего среднего (АРИСС).

1.2. Этапы построения моделей

Дж.Бокс и Г.Дженкинс (1974) предлагают следующие этапы построения моделей динамики для целей прогнозирования или управления:

·                    постулирование общего класса моделей, когда из теоретических и практических соображений и поставленной цели моделирования выбирается полезное семейство гипотетической модели;

·                    структурная идентификация конкретных подклассов выбранных типов моделей с использованием статистических характеристик временных рядов (например, на основе анализа графиков автокорреляционной функции и спектра);

·                    оценка параметров идентифицированных моделей;

·                     диагностическая проверка адекватности конкретной модели

Если в результате диагностики модели были обнаружены дефекты подгонки, последние три этапа итеративно повторяются.

Идентификация - это процедура определения конкретного типа параметрической модели, поскольку общий класс стохастических моделей слишком обширен для непосредственной подгонки к данным. В моделях АР и СС идентификация заключается в выборе периода упреждения l. Задачей идентификации является и выбор наименьшего возможного числа параметров модели при условии ее достаточной адекватности (принцип экономичности модели - parsimony - см. Введение). Например, использование завышенного порядка разности, как будет показано ниже (см. разд. 2.4.5), приводит к заметному росту дисперсии прогноза. Очевидно, что процесс идентификации неизбежно неточен, поскольку основывается на "неточных" непараметрических критериях. На этом этапе особенно полезны суждения с использованием графических методов, хотя дать конкретные рекомендации по анализу коррелограмм и спектров чрезвычайно трудно. Дж.Бокс и Г.Дженкинс предлагают, например, взять за визуальный критерий стационарности быстрое убывание значений выборочной автокорреляционной функции, но само понятие "быстрое убывание" неформализуемо и целиком зависит от опыта и субъективных представлений исследователя.

Стохастические модели временных рядов основываются на некотором множестве коэффициентов (параметров), значения которых должны оцениваться по результатам наблюдений. Здесь используются разные по форме оценки целевой функции оптимизации (чаще всего условный или безусловный методы наименьших квадратов). Наиболее популярен для оптимизации целевой функции при построении моделей АР и СС алгоритм Маркварда, причем для нахождения начального приближения используются уравнения Юла-Уокера, связывающие коэффициенты модели с теоретическими значениями АКФ. В процессе нахождения оценок модели может возникать вырождение, которое почти неизбежно, когда порядки авторегресии и скользящего среднего в модели неоправданно велики. Если же в этом случае и не возникнут вычислительные проблемы, то скорее всего часть оцененных параметров не будет значимо отличаться от нуля.

Если процесс оценивания успешно осуществлен, возникает проблема оценки качества построенной модели. Для "хорошей" модели остатки должны быть "белым шумом", т.е. их выборочные коэффициенты автокорреляции не должны значимо отклоняться от нуля. Кроме того, модель не должна содержать лишних параметров, т.е. желательно уменьшать число параметров, пока не появится значимая автокорреляция остатков. Для диагностики модели необходимо попытаться модифицировать ее, меняя порядки АР и СС, однако опасно повышать оба порядка одновременно ввиду возрастания вероятности вырождения.

1.3. Модель авторегрессии

В авторегрессионной модели порядка p любое текущее значение процесса y_t выражается как конечная линейная совокупность p предыдущих значений процесса и импульса a_t (уровни ряда регрессируют на своих предыдущих значениях):

y_t = φ ₁ y_t-1 + φ ₂ y_t-2 + ... + φ _p y_t-p + a_t

где y_t = x_t - φ . Эта модель содержит p + 2 неизвестных параметра: коэффициенты многочлена φ ₁, ... , φ _p, "средний уровень" процесса φ и дисперсию φ_a² белого шума, которые на практике следует оценить по наблюдениям.

Процесс y_t стационарен, если все корни полинома

 (B) = 1 - φ ₁ B - φ ₂ B² - ... - φ _p B^p ,

где В - оператор сдвига назад; B y_t = y_{t -1}, лежат внутри единичного круга |y| < 1. При слабых дополнительных предположениях стационарный процесс удовлетворяет уравнению авторегрессии бесконечного порядка, с достаточно быстро убывающими коэффициентами.

Модель АР(1) при положительном коэффициенте автокорреляции представляет собой колебательный процесс с преобладанием длинных волн: в спектре подобного процесса присутствует подъем в области низких частот. Если коэффициент автокорреляции отрицателен, процесс является сильно осциллирующим, т.е. в спектре имеются пики в области высоких частот.

Модель АР(2) ведет себя по-разному в зависимости от того, являются ли корни соответствующего полинома действительными или мнимыми. В случае мнимых корней мы получим колебательный процесс с ярко выраженным периодом, а спектр модели будет содержит пик на соответствующей частоте. Неплохой пример подобного процесса - это колебания маятника под действием случайных возмущений. В случае действительных корней процесс АР(2) похож на процесс АР(1).

Например, для ряда NCAL можно предложить гипотетические модели АР(1) -

x_t = 2.086 + 0.3642 (x_{t -1} - 2.086)

и АР(2) -

x_t = 2.106 + 0.4805 (x_{t -1} - 2.106) - 0.3239 (x_{t -2} - 2.106),

а для ряда СКОРОСТЬ - модель АР(1):

x_t = 4.924 + 0.5946 (x_{t -1} - 4.924).

Все коэффициенты моделей являются значимыми по t-критерию, в отличие от моделей более высокого порядка разности (например, АР(3) для ряда NCAL).

Основные характеристики моделей представлены в таблице 1.

Таблица 1

Критерии качества полученных моделей авторегрессии

Характеристика	Ряд/модель
NCAL АР(1)	NCAL АР(2)	СКОРОСТЬ АР(1)
Скорректированный коэффициент детерминации Среднее ряда остатков Стандартная ошибка ряда остатков Статистика Дарбина-Уотсона Тест c-квадрат на "белый шум"	0.1170 0.005529 2.7142 1.760 139.8	0.2022 -0.002817 2.5798 2.104 57.65	0.3496 0.000063 1.7145 2.396 172.3

Очевидно, что модель АР(2) для ряда NCAL имеет существенно лучшие характеристики в смысле ряда остатков, чем модель АР(1).

Модель авторегресии ряда СКОРОСТЬ имеет существенно худшие внутренние показатели, поскольку сам ряд в большей мере имеет нестационарный характер.

1.4. Модель скользящего среднего

Модель скользящего среднего порядка q описывает стационарные процессы как некоторую линейную комбинацию "белого шума" и записывается в виде

y_t = a_t - θ ₁a_{t -1} - θ ₂ a_{t -2} - ... - θ _p a_{t -q} ,

где y_t = x_t - θ . Модель содержит q + 2 неизвестных параметра: коэффициенты многочлена θ₁, ..., θ _q; "средний уровень" процесса θ и дисперсию θ_a² белого шума, которые на практике следует оценить по наблюдениям.

Кроме требований стационарности ряда, практически применима лишь такая форма модели, для которой выполняется условие обратимости: все корни полинома

θ (B) = 1 - θ ₁ B - θ ₂ B² - ... - θ _q B^q ,

лежат внутри единичного круга |y| < 1.

Для теоретического процесса СС(q) все значения автокорреляционной функции для лагов, больших q, равны нулю. Это свойство является характеризационным. Модель СС имеет практическое значение для моделирования процессов, первая (или более высокая) разность которых стационарна. Подобные процессы устроены как случайные колебания с непостоянным средним уровнем (q = 1) или непостоянным углом наклона (q = 2).

1.5. Модель Бокса-Дженкинса (АРИСС)

Модель АРИСС - одну из наиболее популярных моделей для построения краткосрочных прогнозов - часто называют по имени авторов, предложивших методику ее применения для временных рядов, некоторая d-я разность которых стационарна. Модель зависит от трех структурных целочисленных параметров p, d, q [обозначение - АРИСС(p, d, q)] и формально записывается в виде

φ _t = φ ₁ φ _{t -1} + φ ₂ φ _{t -2} + ... + φ _p φ _{t -p} - φ ₁ a_t-1 - φ ₂ a_{t -2} - ... - φ _p a_{t -q} ,

где a_t - "белый шум"; φ _t = (φ ^d x_t) – φ ; φ ^d - оператор взятия разности порядка d, φ - константа, определяющая средний уровень ряда. Параметры φ являются параметрами авторегрессии, а параметры φ - параметрами скользящего среднего.

В общем случае рассматриваются только модели, удовлетворяющие условиям стационарности и обратимости: корни обоих полиномов для φ _i должны лежать внутри единичного круга |y| < 1. Тогда ошибка a_t представляет собой ошибку наилучшего прогноза на шаг вперед. Без условий стационарности и обратимости статистически корректный анализ модели невозможен.

Важными специальными классами моделей АРИСС являются: модель авторегрессии - скользящего среднего АРСС(p, q) = АРИСС(p, 0, q)

y_t = φ ₁ y_{t -1} + φ ₂ y_{t -2} + ... + φ _p y_{t -p} - φ ₁ a_t-1 - φ ₂a_{t -2} - ... - φ _p a_{t -q} ,

где y_t = x_t –φ ; d = 0, а также модель ИСС(d, q) = АРИСС(0, d, q), в которой p = 0. Очевидно, что и модель авторегресии АР(p) можно представить как частный случай АРИСС(p, 0, 0), для которой d = q = 0. Другой частный случай - модель скользящего среднего СС(q), для которой p = d = 0.

Первый шаг идентификации моделей АРИСС - определение порядка разности d, который должен быть выбран так, чтобы ряд φ _t = (φ ^d x_t) был стационарным. Для определения d текущие разности ряда последовательно тестируются на стационарность. На практике часто оказывается, что адекватное описание наблюдаемых временных рядов достигается при помощи моделей, в которых p и q не больше, а часто и меньше 2.

Некоторые результаты прогонки моделей АРИСС для ряда СКОРОСТЬ представлены в таблице 2.

Таблица 2

Критерии качества полученных моделей АРИСС

Характеристика модели	Модель АРИСС
(1,0,1)	(1,1,0)	(2,2,0)
Скорректированный коэффициент детерминации Среднее ряда остатков Стандартная ошибка ряда остатков Статистика Дарбина-Уотсона Тест Хи-квадрат на белый шум	0.4988 0.000715 1.5051 1.965 51.56	0.3656 0.000782 1.6932 2.314 95.19	0.0037 -0.00594 2.1298 2.363 93.28

Очевидно, что учет первого порядка разности - модель АРИСС(1,1,0) - несколько улучшает свойства модели, однако дальнейшее увеличение параметра d приводит к вырождению моделируемого процесса (что является проявлением принципа экономичности моделей). Следует отметить, что модели АРИСС и ИСС не предъявляют жестких требований к стационарности исходного ряда вследствие применения нелинейного фильтра.

Очевидный дефект модели - недостоверность коэффициента авторегрессии, что дополнительно свидетельствует о близости ряда к теоретическому процессу скользящего среднего.

Наилучшая модель АРИСС(3, 0, 0) ряда NH4+ (упоминаемая в дальнейшем изложении как модель R1), полученная перебором всех p, d и q до 3-го порядка, имеет вид

x_t = 17.264 + 0.421 x_{t -1} + 0.15 x_{t -2} + 0.237 x_{t -3} ;

2. Практическая часть

УСЛОВИЕ ЗАДАЧИ

         Исходные данные представлены в таблице 3.

Таблица 3

Исходные данные задачи

№ п/п	Показатель	Обозначение	Значение
1	t – критерий Стьюдента расчетный	t  рас	4,701
2	F – критерий Фишера расчетный	F рас	18,92
3	t – критерий Стьюдента табличный	t таб	5,84
4	F – критерий Фишера табличный	F таб	19,8
5	Стандартное отклонение	S 1.2	19,2
6	Число наблюдений	N	8
7	Горизонт прогнозирования	T	12
8	а	А	2,23
9	В	В	0,897

РЕШЕНИЕ

1)    Устанавливаем величину  доверительных пределов прогноза при  сравнении расчетных и табличных значений критериев Стьюдента (t) из таблицы 1.

t рас ≥ t таб,

Табличное значение t таб  равно 5,84 (из таблиц критерия Стьюдента)

Тогда, 4,701≥ 5,84.

         Так как расчетное значение больше табличного значения критерия Стьюдента, то  предлагаемая модель прогноза соответствует выбранному доверительному интервалу.

2)    Проверяем статистическую значимость модели сравнением расчетного значения критерия Фишера и табличного значения.

F  рас≥ F таб,

18,92≥ 19,8

         Значит, модель прогноза статистически значима  и может применяться.

3)    Рассчитаем точечный прогноз:

У (Т) = а+в*Т,                                 (1)

Т = N +m = 8+2 = 10

Где    m – величина упреждения (равна 2). Значения а и в возьмем из таблицы 1.

         Тогда, У (Т) = 2,23+0,897*10 = 11,2

         Прогнозируемое значение показателя У в 10 м периоде от начала планирования равно 11,2 .

4)    Рассчитаем доверительные интервалы прогноза

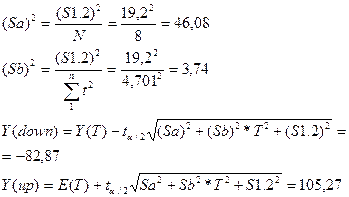
         Выполненная оценка доверительных пределов позволяет сделать вывод о том, что истинное  значение прогнозируемого показателя будет находиться в пределах от -82,87 до 105,27 с вероятностью 0,99, что свидетельствует о низкой точности  модели, используемой для прогнозирования.

В таблице 4 отражена динамика значения  диапазона доверительных пределов  при изменении числа наблюдений N.

Таблица 4

Динамика диапазона доверительных пределов при изменении  числа наблюдений

N	T	Y(T)	Sa2	Sb2	Ydown	Y up
8	10	11,2	46,08	3,74	-82,87	105,27
9	11	12,097	40,96	3,62	-82,52	106,71
10	12	12,994	36,864	3,51	-82,68	108,67
11	13	13,891	33,5127	3,41	-83,38	111,16
12	14	14,788	30,72	3,32	-84,00	113,58
13	15	15,685	28,3569	3,23	-85,20	116,57
14	16	16,582	26,3314	3,15	-86,66	119,83
15	17	17,479	24,576	3,07	-88,07	123,02
16	18	18,376	23,04	3,00	-89,40	126,15
17	19	19,273	21,6847	2,93	-91,04	129,58
18	20	20,17	20,48	2,86	-92,62	132,96
19	21	21,067	19,4021	2,80	-94,14	136,27
20	22	21,964	18,432	2,74	-95,59	139,52

Как видно из таблицы 4, с ростом числа наблюдений   значения нижних и верхних границ интервалов растут.

ОТВЕТ

         Истинное значение прогнозируемого показателя будет находиться в пределах от -82,87  до 105,27 с вероятностью 0,99.

Список литературы

1.     Бешелев С.Д., Гурвич Ф.Г. Экспертные оценки в принятии плановых решений. – М.: Экономика, 1976

2.     Бигель Дж. Управление производством: количественный подход. – М.: Мир, 1973

3.     Дрейпер Н., Смит Г. Прикладной регрессионный анализ. – М.: Статистика, 1973

4.     Кобринский Н.Е., Майминас Е.З., Смирнов А.Д. Введение  в экономическую  кибернетику. – М.: Экономика, 1975

5.     Математика и кибернетика в экономике: Словарь – справочник. – М.: Экономика, 1975

6.     Мот Ж. Статистические методы приведения и решения  на предприятии. – М.: Прогресс, 1966

7.     Организация производства на промышленных предприятиях США/ Под ред. Хейнмана С.А.- М.: Прогресс, 1969

8.     Риггс Дж. Производственные системы: планирование, анализ, контроль. – М.: Прогресс, 1972

9.     Саркисян С.А., Акопов П.Л., Мельникова Г.В. Научно- техническое прогнозирование и программно- целевое планирование. – М.: Машиностроение, 1987

10.                       Тейл Г. Экономические прогнозы и принятие решений. – М.: Статистика, 1971

11.                       Четыркин Е.М. Статистические  методы прогнозирования. – М.: Статистика, 1974