Содержание

1. Сформулируйте закон сохранения импульса в классической механике и свяжите его с законом динамики Ньютона. Приведите пример использования того закона. Как он связан со свойствами пространства-времени. ………………3

2. Как измеряются расстояния в микромире? Дайте понятие о метрической системе. Где на Земле можно наиболее приблизиться к центру Земли?. ………..6

3. Дайте представление о модели гармонического осциллятора и использовании этой модели. Что такое «когерентность», «резонанс», «поляризация»?. ………...9

4. В чем суть законов Кеплера? Поясните их связь с законом всемирного тяготения. Насколько применима модель, принятая Ньютоном? Что такое «лапласовский детерминизм. ……………………………………………………...10

5. В каких единицах измеряются энергия, работа и мощность? Как эти величины связаны между собой и что они характеризуют? Что такое механический эквивалент теплоты? Какие виды энергии Вы знаете? В каких системах она сохраняется и как закон сохранения энергии связан со свойствами пространства-времени. ……………………………………………………………..12

6. Как соединяются атомы в молекулы? Какие виды химической связи Вам известны, какова их энергетическая значимость? Какова роль энергии и энтропии в образовании молекул?. ………………………………………………...14

7. Опишите спектр электромагнитного излучения. Как были открыты инфракрасное и ультрафиолетовое излучение, рентгеновские лучи?. ………….16

8. Поясните особую роль математики и моделирования в естествознании. Как осуществляется математическое моделирование биологической эволюции?. …18

9. Дайте определение «экосистеме» и «трофическому уровню». Поясните, как происходит передача энергии вверх по трофическим уровням экосистем…….20

10. Как происходит обмен веществ и энергией в живой клетке? Чем он отличается от обменных процессов в неживой природе? Как Вы представляете человека как предмета обществоведения и естествознания? Насколько можно применить естественнонаучные модели к общественным процессам?. ………..21

Список литературы. ………………………………………………………………..23

1. Сформулируйте закон сохранения импульса в классической механике и свяжите его с законом динамики Ньютона. Приведите пример использования того закона. Как он связан со свойствами пространства-времени, и почему этот закон фундаментален?

Момент импульса системы тел сохраняется неизменным при любых взаимодействиях внутри системы, если результирующий момент внешних сил, действующих на нее, равен нулю.

Закон сохранения импульса является следствием законов Ньютона, являющихся основными законами динамики. Однако этот закон универсален и имеет место и в микромире, где законы ньютона неприменимы.

Следствия:

1) В случае изменения скорости вращения одной части системы другая также изменит скорость вращения, но в противоположную сторону таким образом, что момент импульса системы не изменится;

2) Если момент инерции системы в процессе вращения изменяется, то изменяется и ее угловая скорость таким образом, что момент импульса системы останется тем же самым;

3) В случае, когда сумма моментов внешних сил относительно некоторой оси равняется нулю, момент импульса системы относительно этой же оси остается постоянным.

Примеры:

К первому следствию - при движении человека, находящегося на поверхности диска, по окружности с центром, совпадающим с центром масс диска, последний начинает поворачиваться в сторону, противоположную движению человека относительно Земли;

Ко второму следствию – допустим человек, держащий в вытянутых расправленных руках гантели, сидит на скамье, которая вращается вокруг вертикальной оси. В случае приближения гантелей к груди угловая скорость движения системы «скамья-человек-гантели» увеличивается.

К третьему следствию - в начальный момент времени человек сидит на неподвижной скамье и удерживает в руках раскрученное колесо. Причем ось вращения колеса перпендикулярна оси вращения Z скамьи, т. е. расположена в горизонтальной плоскости. При повороте колеса на 90^о в вертикальной плоскости проекция момента импульса системы «скамья-человек-колесо» на вертикальную ось L_zне изменится и останется равной нулю.

L_z = L_{z студ} + L_z кол = L_z0 = 0, т.е. L_{z студ} = - L_z кол.

Следовательно, вектора угловых скоростей системы «человек-скамья» и колеса направлены в противоположные стороны[1].

Импульсом тела или количеством движения называют произведение массы тела на его скорость. P – векторная величина. Направление импульса тела совпадает с направлением скорости.

Совокупность тел взаимодействующих между собой и рассматриваемых как единое целое, называют механической системой. Силы, действующие в механической системе, подразделяются на две группы: внутренние силы, т.е. силы взаимодействия между телами, входящими в систему, и внешние силы, т.е. силы, действующие на тела системы со стороны тел, не принадлежащих ей. Если на механическую систему внешние силы не действуют или их равнодействующая сила равна нулю, то такую систему называют замкнутой (или изолированной).

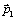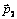Рассмотрим замкнутую механическую систему, состоящую только из двух тел. Пусть импульсы этих тел равны и . В какой-т момент времени они сталкиваются. В результате импульс первого тела становится равным 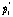, а второго 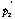. Во время удара на первое тело действует сила 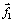, а на второе - 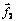, которые, согласно третьему закону Ньютона, равны по модулю и противоположны по направлению, т.е. 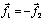. Под действием этих сил изменяются импульсы взаимодействующих тел. Используя второй закон Ньютона, запишем: 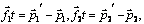где t – время, в течение которого действуют силы, равное времени соударения тел. Но 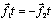, поскольку, согласно третьему закону Ньютона 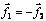. С учетом этого получаем 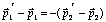. Отсюда, 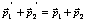. Левая часть этого равенства представляет собой импульс механической системы после взаимодействия (после столкновения тел), а правая – до взаимодействия. Поэтому можно сделать вывод, что импульс замкнутой механической системы, состоящей из двух тел не меняется. Это справедливо и для механической системы. Состоящей из любого числа тел. Итак, импульс замкнутой механической системы постоянен при любых взаимодействиях тел, принадлежащих этой системе, т.е. 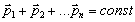- закон сохранения импульса.

Можно назвать много явлений, в основе которых лежит закон сохранения импульса - отдача орудий и огнестрельного оружия при выстреле, действие реактивных двигателей и т.д. В механике закон сохранения импульса является следствием законов Ньютона, являющихся основными законами динамики. Однако этот закон универсален и имеет место и в микромире, где законы Ньютона неприменимы.

Установленные в наше время связи между свойствами пространства и времени и законами сохранения импульса содержались в скрытой форме и в принципах классической механики Галилея – Ньютона. Галилей рассматривал пространство и время как реальности, которые существуют вне человеческого сознания. Открытый им принцип однородности отражал однородность и изотропность пространства. У Ньютона пространство и время абсолютны в том смысле, что свойства пространства не зависят от движущихся в нем тел и протекающих механических явлений, а свойства времени – от движущейся материи. Пространство и время не связаны между собой, они представляют как бы арену, где происходят события. Однородность и изотропность пространства и времени необходимо следуют из законов Ньютонов.

В последствии оказалось, что законы Ньютона можно заменить единым постулатом – вариационным принципом, который был удобнее во многих отношениях, в частности, в том, что его можно использовать при формулировке сложных задач. В механике материальной точки этот постулат равноценен законам Ньютона[2].

2. Как измеряются расстояния в микромире? Дайте понятие о метрической системе. Где на Земле можно наиболее приблизиться к центру Земли?

Следует отметить, что микромир нельзя рассматривать как некий уменьшенный масштаб макропроцессов, т.к. явления микромира подчиняются другим закономерностям и изменяются на основе иных принципов.

Макромир характеризуется, прежде всего, огромными массами и относительно малыми скоростями движения, в микромире малые массы, но высокие скорости движения. Для макромира характерны большие расстояния вплоть до бесконечности, а взаимодействие в микромире имеют размеры сопоставимые с размером ядер. Время, в макромире порядок времени, единицы измерения известны, но в микромире мы имеем дело с планковскоми временами, которые очень малы, коротки. Когда рассматривают здесь времена надо рассматривать с позиции квантовой механики.

Метрическая система - десятичная система мер и весов, возникшая во Франции. Основной единицей этой системы является метр, приблизительно равный одной десятимиллионной части расстояния по меридиану от экватора до полюса, или около 39,37 дюйма.

Масштабы за пределом размера атома уже недоступны непосредственному измерению. То есть так, как здесь, метр приложить мы не можем, это уже какие-то косвенные измерения в рамках некоторых теоретических предположений. То есть мы предполагаем какую-то структуру пространства-времени на этих расстояниях, и вот потом, используя эти теоретические представления, мы энергию или передачу импульса переводим в расстояние.

И вот когда мы говорим о том, что достигаем какого-то расстояния, фактически реально это означает, что мы наблюдаем процесс с какой-то передачей импульса. И процесс с такой передачей импульса, по нашим теоретическим представлениям, отвечает тому, что мы достигаем каких-то расстояний. Так вот, после примерно 10 в минус 8-й, вся информация о пространстве-времени – это уже косвенная информация, мы ничего там непосредственно глазом или микроскопом увидеть не можем. Метрическая система – это общее название международной десятичной системы единиц, основными единицами которой являются метр и килограмм. При некоторых различиях в деталях элементы системы одинаковы во всем мире.

На больших расстояниях, когда величиной R_g / R можно пренебречь по сравнению с единицей, выражение для интервала переходит в интервал СТО, записанный в сферической системе координат, а именно

dS ² = c²dt ² - dR² - R²(dq ² + sin² q dj ² );(1)

Метрика Шварцшильда описывает в хорошем согласии с экспериментом три известных эффекта: смещение перигелия орбиты планеты, отклонение луча света Солнцем и гравитационное красное смещение спектральных линий. Однако теперь мы видим, что в малых (планковских) масштабах интервал (1) неизбежно должен иметь вид

dS ² = (1 - 2l²_пл / R²) c²dt ² - dR² / (1 - 2l²_пл / R²) - R ²(dq ² + sin² q dj ² );….(2)

Из (2) видно, что даже в микромире вплоть до расстояний 10 ^-30 см мы с большой точностью все еще можем пользоваться интервалом (1), т.е. вплоть до этих расстояний справедливы соотношения специальной теории относительности.

Для измерения макроскопических расстояний в настоящее время используется эталон метра, равный расстоянию, которое проходит луч света в вакууме за 1/299792458-ую долю секунды. Cледует отметить, что таким образом эталон метра привязан к эталону секунды. Такой стандарт, однако, непригоден в микромире, когда речь идет об измерении атомных расстояний: просто длина волны видимого света слишком велика для таких измерений. Поэтому здесь требуется иной эталон: не противоречащий, разумеется, основному определению метра, но удобный для практического измерения расстояний порядка межатомных.

Сейчас таким «опорным расстоянием» является постоянная кристаллической решетки (т.е., в данном случае - расстояние между ближайшими атомами в решетке) чистого кремния, которая равна a = 5,43102088х10^-10 м с точностью 0,03 ppm. Все бы хорошо, но только этот стандарт крайне трудно воспроизвести в лаборатории. В самом деле, во-первых, расстояние между атомами в решетке зависит от температуры и давления. В частности, это значение a отвечает температуре 22,500 °C (295,650 K), стабильной в пределах < 1 mK. Кроме того, для создания этого эталона необходим сверхчистый кремний: любые примеси и неоднородности будут искажать кристаллическую решетку вокруг себя. Именно поэтому продолжаются попытки найти иной эталон для измерения атомных расстояний, имеющий точность, сравнимую с «кремниевым» стандартом, и вдобавок не столь требовательный к внешним условиям.

Природа жидкости по Архимеду такова, «что из ее частиц, расположенных на одинаковом уровне и прилегающих друг к другу, менее сдавленные выталкиваются более сдавленными, и что каждая из ее частиц сдавливается жидкостью, находящейся над ней, по отвесу». Это определение позволяет Архимеду сформулировать основное положение: «Поверхность всякой жидкости, установившейся неподвижно, будет иметь форму шара, центр которого совпадает с центром Земли».

Таким образом, Архимед считает Землю шаром и поверхность тяжелой жидкости, находящейся в равновесии в поле тяжести Земли, сферической. Он доказывает далее, что тела одинакового удельного веса с жидкостью (он называет их «равнотяжелыми с жидкостью») погружаются настолько, что их поверхность совпадает с поверхностью жидкости. Более легкое тело погружается настолько, что объем жидкости, соответствующий погруженной части тела, имеет вес, равный весу всего тела. Путем логических рассуждений Архимед приходит к предположениям, содержащим формулировку его закона:

«Тела более легкие, чем жидкость, опущенные в эту жидкость насильственно, будут выталкиваться вверх с силой, равной тому весу, на который жидкость, имеющая равный объем с телом, будет тяжелее этого тела».

3. Дайте представление о модели гармонического осциллятора и использовании этой модели. Что такое «когерентность», «резонанс», «поляризация»?

Гармоническим осциллятором называется система, способная совершать гармонические колебания. В физике модель гармонического осциллятора играет важную роль, особенно при исследовании малых колебаний систем около положения устойчивого равновесия. Примером таких колебаний в квантовой механике являются колебания атомов в твердых телах, молекулах и т.д.

Важным отличием осциллятора является то, что движение частицы не ограничено какой-либо непроницаемой стенкой. Поэтому у осциллятора нет граничных условий, подобных граничным условиям потенциальной ямы. Единственным требованием, которое налагается на волновую функцию осциллятора, является требование её квадратичной интегрируемости.

Когерентность (от лат. cohaerens - находящийся в связи) - согласованное протекание во времени нескольких колебательных или волновых процессов. Если разность фаз 2 колебаний остается постоянной во времени или меняется по строго определенному закону, то колебания называются когерентными. Колебания, у которых разность фаз изменяется беспорядочно и быстро по сравнению с их периодом, называются некогерентными.

Резонанс – (от франц. resonance, от лат. resono – откликаюсь), резкое возрастание амплитуды установившихся вынужденных колебаний при приближении частоты внешнего гармонического воздействия к частоте одного из собственных колебаний системы.

Поляризация - это ориентированность колебаний световой волны в пространстве. Эти колебания перпендикулярны направлению движения луча света. Элементарная световая частица (квант света) представляет собой волну, которую можно сравнить для наглядности с волной, которая побежит по канату, если, закрепив один его конец, другой встряхнуть рукой. Направление колебаний каната может быть различным, смотря по тому, в каком направлении встряхивать канат. Точно так же и направление колебаний волны кванта может быть разным. Пучок света состоит из множества квантов. Если их колебания различны, такой свет не поляризован, если же все кванты имеют абсолютно одинаковую ориентацию, свет называют полностью поляризованным. Степень поляризации может быть различной в зависимости от того, какая доля квантов в нем обладает одинаковой ориентацией колебаний[3].

4. В чем суть законов Кеплера? Поясните их связь с законом всемирного тяготения. Насколько применима модель, принятая Ньютоном? Что такое «лапласовский детерминизм»?

Законы Кеплера - прямо скажем непростые законы. Потом появился закон всемирного тяготения, для которого законы Кеплера стали частными случаями. Закон этот конечно выглядит проще. С другой стороны с таким же успехом можно было бы набрать огромное количество таблиц с численными значениями всевозможных траекторий небесных тел. Было бы это законом?

Движение вокруг Солнца описывается законами Кеплера. Эти законы математически выводятся из закона всемирного тяготения.

Первый закон Кеплера. Орбита каждой планеты есть эллипс, в одном из фокусов которого находится Солнце.

Второй закон Кеплера (см. рис. 2). Радиус-вектор планет за равные промежутки времени описывают равные площади.

Р₂

Р₁

Р₃

Р₄

Рис. 2. Второй закон Кеплера. Линия SР соединяет планету с Солнцем. Дуги Р₁Р₂ и Р₃Р₄ планета проходит за одинаковое время. площадь сектора SР₁Р₂ равна площади сектора SР₃Р₄

Третий закон Кеплера. Квадраты периодов обращения двух планет относятся как кубы больших полуосей их орбит.

Законы Кеплера применимы не только к движению планет, но и к движению их естественных и искусственных спутников[4].

Представления о незыблемости научных законов, о неограниченности их линейной экстраполяции в пространстве и во времени сохраняют статус признаков научности. Между тем их неявным основанием является концепция лапласовского детерминизма, применимая благодаря линейности математических уравнений, что связано с идеализирующими допущениями о неизменности исследуемых объектов и условий их существования. Связь между такими идеализирующими допущениями и методологическими принципами становится очевидна лишь в свете дальнейшего развития науки, но ее осознание требует дополнительных методологических усилий.

Идеал лапласовского детерминизма вдохновлял творцов теорий скрытых параметров десятилетия после создания квантовой механики и разработки концепции вероятностной причинности вплоть до осуществленного в самое последнее время экспериментального доказательства полноты квантовой механики.

Кеплеровские законы были уточнены и объяснены на основе закона всемирного тяготения Исааком Ньютоном. Закон же всемирного тяготения гласит:

Сила F взаимного притяжения между материальными точками массами m1 и m2, находящиеся на расстоянии r друг от друга, равна: F=Gm1m2/r^2, где G - гравитационная постоянная. Закон открыт Ньютоном также в XVII веке (понятно, что на основе законов Кеплера).

Таким образом в формулировке Ньютона законы Кеплера звучат так:

первый закон: под действием силы тяготения одно небесное тело может двигаться по отношению к другому по окружности, эллипсу, параболе и гиперболе. Надо сказать, что он справедлив для всех тел, между которыми действует взаимное притяжение.

формулирование второго закона Кеплера не дана, так как в этом не было необходимости.

третий закон Кеплера сформулирован Ньютоном так: квадраты сидерических периодов планет, умноженные на сумму масс Солнца и планеты, относятся как кубы больших полуосей орбит планет.

5. В каких единицах измеряются энергия, работа и мощность? Как эти величины связаны между собой и что они характеризуют? Что такое механический эквивалент теплоты? Какие виды энергии Вы знаете? В каких системах она сохраняется и как закон сохранения энергии связан со свойствами пространства-времени?

Энергия – скалярная физическая величина, являющаяся общей мерой различных форм движения материи. Иными словами энергия – это просто число, рассчитываемое по определенным правилам. И природа нашей Вселенной такова, что суммарная энергия замкнутой системы с течением времени не изменяется. Как показал Эйнштейн, полная энергия системы, имеющей массу М, равна Е=Мс², где с – скорость света в вакууме. Количество потребляемой энергии измеряется в ваттах (Вт).

Работа измеряется в Джоулях (Дж). 1 Дж- работа, совершаемая силой в 1Н на пути, равном 1 м, при условии, что направление силы и перемещения совпадают. [Дж]=[Н м].

Мощность измеряется в Ваттах (Вт). 1 Вт- мощность при совершенной работе в 1 Н за время 1 с. В кВА измеряется полная мощность, в кВт измеряется только активная мощность. Полная мощность – есть алгебраическая сумма активной и реактивной мощности.

Механический эквивалент теплоты - количество работы, энергетически эквивалентное единице количества теплоты. Механический эквивалент теплоты равен 4,1868 Дж/кал. В Международной системе единиц (СИ), в которой единицей количеств теплоты и работы является джоуль, механический эквивалент теплоты = 1.

Виды энергии.

Внутренняя энергия – это часть полной энергии системы, заключенная в самой системе веществе тел, образующих систему. Она подразделяется на несколько уровней в зависимости от характера процессов, приводящих к ее изменению.

Энергия органического топлива (нефти, природного газа, каменного угля, торфа и дерева), высвобождение которой и создало современную цивилизацию, представляет собой энергию химических связей органических молекул, запасенную в ходе процесса развития жизни на Земле за рошедшие сотни миллионов лет.

Энергия взаимодействия нуклонов (протонов и нейтронов) в ядрах атомов обусловлена сильным взаимодействием. Масса ядра всегда меньше суммы масс, входящих в него частиц. Это обусловлено тем, что при объединении нуклонов в ядро выделяется энергия связи нуклонов друг с другом.

Свойства симметрии пространства и времени подтверждают их единство. Действительно, изменение импульса, сохранение которого связано с однородностью пространства, согласно второму закону Ньютона определяется такой временной характеристикой, как импульс силы, равный произведению FхDt. С другой стороны, изменение энергии, сохранение которой связано с однородностью времени, определяется такой пространственной характеристикой, как работа А_1-2= (F, Dr)[5].

6. Как соединяются атомы в молекулы? Какие виды химической связи Вам известны, какова их энергетическая значимость? Какова роль энергии и энтропии в образовании молекул?

Атомы образуют химическую связь между собой посредством перекрывания электронных облаков. В образовании химической связи участвуют неспаренные электроны внешнего электронного слоя. Иногда связь может образовываться и с помощью пары электронов. Электроны внешнего слоя называют валентными электронами. Два электрона (по одному от разных двух атомов) с противоположным спином объединяются и образуют общую электронную пару, которая располагается между ядрами двух атомов. Оба положительно заряженных ядра атомов будут притягиваться к отрицательной электронной паре, а значит, и друг к другу. Так образуется из двух отдельных атомов самая простая двухатомная молекула - молекула водорода.

Если на внешнем электронном слое есть несколько неспаренных электронов, то атом образует и несколько общих электронных пар, то есть несколько связей. Число связей и определяет значение валентности атома. Таким образом, значение валентности атома зависит от числа неспаренных электронов на внешнем электронном слое атома.

Если в результате соединения атомов образуются общие электронные пары, то такую химическую связь называют ковалентной. Ковалентная связь - это связь между атомами, при которой образуются одна или несколько общих электронных пар.

Ковалентная связь бывает двух видов - ковалентная неполярная и ковалентная полярная. Связано такое деление с тем, где именно между ядрами будут располагаться общие электронные пары - ровно посередине или будут смещены в сторону одного из ядер.

Правее стоящий в этом ряду элемент обладает большей электроотрицательностью и лучше стягивает в свою сторону общие электронные пары.

Если молекула состоит из одинаковых атомов (или атомов одного вида), электроотрицательность которых равна, то общие электронные пары будут находиться посередине между ядрами двух связывающихся атомов, поскольку ядра притягивают общие электронные пары с равной силой. В этом случае между атомами образуется ковалентная неполярная связь. Ковалентная неполярная связь образуется в таких молекулах как Н₂, О₂, N₂ и т.д.

Ковалентная неполярная связь образуется между атомами неметаллов с одинаковой электроотрицательностью (проще говоря, между одинаковыми атомами), общие электронные пары расположены посередине между ядрами двух атомов.

Если молекула состоит из атомов разных неметаллов, электроотрицательность которых различна, то общие электронные пары будут смещены в сторону ядра атома с большей электроотрицательностью, поскольку ядро более электроотрицательного атома сильнее притягивает общие электронные пары. В этом случае между атомами образуется ковалентная полярная связь. Молекула становится диполем - частицей с двумя полюсами: на одном конце некоторый положительный заряд, на другом - некоторый отрицательный. Ковалентная полярная связь образуется в таких молекулах как H₂O, HCl, CO₂, H₂S и т.д.

Особенностью биосистем является то, что в них практически нет обратимых процессов. Все процессы, которые в них протекают, носят необратимый характер, то есть сопровождаются увеличением энтропии. Следовательно, в биосистемах не вся затрачиваемая при данном процессе свободная энергия переходит в полезную работу. Часть ее рассеивается в виде тепла. Отношение количества совершенной работы к количеству затраченной на нее свободной энергии называется коэффициентом полезного действия биологического процесса. Так, мышечное сокращение совершается с КПД ~ 30%, гликолиз ~ 36% и т.д. Как видим, потери свободной энергии при этих процессах весьма велики. Встречаются, однако, и такие процессы, которые близки к обратимым, то есть КПД которых высок. Например, свечение некоторых тропических насекомых имеет КПД 98-99%, разряд электрических рыб – 98%. Причина такого высокоэффективного использования свободной энергии пока не совсем ясна. Таким образом, мы приходим к выводу, что, чем больше увеличение энтропии при данном процессе, тем более он необратим[6].

7. Опишите спектр электромагнитного излучения. Как были открыты инфракрасное и ультрафиолетовое излучение, рентгеновские лучи?

Весь спектр электромагнитного излучения включает в себя как рентгеновские лучи, ультрафиолетовые и видимые лучи, занимающие совсем небольшой диапазон, инфракрасный свет и волны, с которыми мы встречаемся ежедневно: ТВ, радио и электрические.

Открытие инфракрасного излучения произошло в 1800 г. Английский учёный В. Гершель обнаружил, что в полученном с помощью призмы в спектре Солнца за границей красного света (т. е. в невидимой части спектра) температура термометра повышается.

Термометр, помещённый за красной частью солнечного спектра, показал повышенную температуру по сравнению с контрольными термометрами.

Было доказано, что инфракрасное излучение подчиняется законам оптики и, следовательно, имеет ту же природу, что и видимый свет. В 1923 советский физик А. А. Глаголева-Аркадьева получила радиоволны с длиной волны приблизительно равной 80 мкм, т. е. соответствующие инфракрасному диапазону длин волн. Таким образом, экспериментально было доказано, что существует непрерывный переход от видимого излучения к инфракрасному излучению и радиоволновому и, следовательно, все они имеют электромагнитную природу.

Открытие ультрафиолетового излучения. В середине XIX века человек по имени Генрих Гейслер открыл, что когда электрический заряд под высоким напряжением проходит через вакуум в трубке, получался красивый световой эффект. Позднее сэр Уильям Крукс доказал, что причиной светового эффекта были электризованные частицы.

История открытия рентгеновских лучей начинается с того дня, когда физик Рентген прервал нормальное исследование катодных лучей, поскольку заметил, что экран, покрытый платиносинеродистым барием, на некотором расстоянии от экранирующего устройства светился во время разряда. Дальнейшее исследование (оно заняло семь изнурительных недель, в течение которых Рентген редко покидал лабораторию) показало, что причиной свечения являются прямые лучи, исходящие от катодно-лучевой трубки, что излучение дает тень, не может быть отклонено с помощью магнита и многое другое. До того как Рентген объявил о своем открытии, он пришел к убеждению, что этот эффект обусловлен не катодными лучами, а излучением, в некоторой степени напоминающим свет[7].

8. Поясните особую роль математики и моделирования в естествознании. Как осуществляется математическое моделирование биологической эволюции?

Применения математики, столь же характерно для современного естествознания как применение экспериментальных методов, логическая стройность, строго дедуктивный характер построений, общеобязательность выводов математики, делали ее прекрасной опорой для естествознания. Достоинство математизации естество знания чрезвычайно многообразны. Во-первых, во многих случаях математика играет роль универсального языка естествознания, прекрасно подходящего для лаконичной и точной фиксации различных положений. Во-вторых, математика может служить источником моделей, алгоритмических схим, для связей, отношений и процессов, составляющих предмет естествознания. Разумеется любая математическая модель это своего рода упрощение, но упрощение в данном случае не тождественно огрублению, это скорее выявление сущностных особенностей объекта. Поскольку в математических формулах и уравнениях воспроизведены некие общие связи и отношения, реального мира, они могут повторяться в разных его областях. На этом построен метод естественно научного исследования, который называют математической гипотезой, в ней не создают математическое описание природных объектов, а пытаются готовой математической модели подобрать соответствие в природе. Часто исходная математическая формула заимствуется из смежной и даже не смежной области знания, в нее подставляются значения, иной природы, а затем проверяют, совпадение рассчитанного и реального поведения объекта.

В целом значение математики в современном естествознании невозможно переоценить, сейчас ни одна теоретическая интерпретация не считается полностью завешенной, если не удается создать математическую модель изучаемого явления. Однако не следует думать, что все естествознание может быть сведено к математике, построение формальных систем, моделей, алгоритмических схем, это только метод, одна из сторон научного поиска. Развивается наука прежде всего как содержательное, неформализованное, неалгоритмизироанное знание.

Согласно современным представлениям, жизнь на Земле возникла примерно 3,5 млрд. лет назад после предбиологической эволюции в форме прогенот, простейших одноклеточных бактериоподобных структур. Около 2 млрд. лет назад на эволюционном древе появились три ветви: безъядерных эубактерий и архибактерий, и эукариот, клетки которых имеют ядро. Эубактерии и архибактерии в дальнейшем совершенствовались только на метаболическом уровне, в то время как эукариоты развивались на уровне морфологическом и физиологическом

Проблема состоит в том, чтобы понять, каким образом в линии эукариот нарастала сложность, как и где эта сложность кодировалась, каковы механизмы, приведшие от простейших систем к очень сложным организмам.

Прогрессивная эволюция - это эволюция регуляторных генетических систем организмов. В основе кодирования генетической сложности лежит комбинаторный принцип, позволяющий очень экономно записывать в геномах огромное количество информации о генетических программах, выполняемых генными сетями. Комбинаторный принцип, буквально пронизывающий кодирование генетических программ функционирования высших эукариот, способен обеспечивать в ходе эволюции быстрое, скачкообразное появление новых морфотипов за счет переключения уже существующих программ онтогенеза[8].

9. Дайте определение «экосистеме» и «трофическому уровню». Поясните, как происходит передача энергии вверх по трофическим уровням экосистем. Какие модели описывают отношения между трофическим уровнями в биоценозах?

Совокупность всех организмов и растений, обитающих в данной местности и зависящих друг от друга в различных отношениях, и окружающей эти организмы физической и химической среды называется экосистемой.

Разные уровни питания экосистемы называют трофическими уровнями (от греч. трофее – питание, пища). Первый трофический уровень образует продуценты (растения), второй – первичные консументы (растительноядные животные), третий – вторичные консументы (плотоядные, поедающие растительноядных) и т.д. Многие животные питаются более чем на одном трофическом уровне, поедая как растения, так и первичных консументов или как первичных консументов, так и вторичных консументов.

Таким образом, энергия солнечного света передается вверх по трофическим уровням пищевой сети экосистем. Но всякий раз, когда происходит превращении энергии – энергии солнечных лучей в химическую энергию органических веществ, этой последней – в энергию, необходимую для поддержания жизнедеятельности организма, - некоторая доля полезной энтропии, рассеивается в виде бесполезной тепловой энергии. Каждый организм использует какое-то количество энергии на поддержание собственного существования и на рост, оставляя все меньше энергии, доступной организмам следующего трофического уровня. Это означает, что на высших трофических уровнях количество ее невелико. Поэтому пищевые сети редко состоят более чем из 4-5 трофических уровней: растения, растительноядные животные и два или три уровня плотоядных.

Примеры. Пастбищная пищевая сеть: клевер (продуцент) – овца – волк. Планктонная пищевая сеть: водоросли – дафния – плотва – щука – скопа.

По мере повышения трофического уровня характерно увеличение размеров особей при одновременном уменьшении плотности популяции, скорости размножения и биомассы. Такие животные, как, например, волки или тигры, находятся на самой вершине пищевой сети, питаясь растительноядными или мелкими плотоядными животными. Волку иногда приходится преодолевать по 30 километров в день, чтобы добыть себе пищу, а площадь индивидуальной территории тигра может достигать 300 км². организмы, питающиеся на этих хищниках высшего порядка – паразитические черви и блохи, - фактически получают только жалкие крохи от «энергетического пирога» экосистемы[9].

10. Как происходит обмен веществ и энергией в живой клетке? Чем он отличается от обменных процессов в неживой природе? Как Вы представляете человека как предмета обществоведения и естествознания? Насколько можно применить естественнонаучные модели к общественным процессам?

Обмен веществ и энергии - основное свойство живого. В цитоплазме клеток органов и тканей постоянно идет процесс синтеза сложных высокомолекулярных соединений и одновременно с этим - их распад с выделением энергии и образованием простых низкомолекулярных веществ - диоксида углерода, воды, аммиака и др. Процесс синтеза органических веществ называется ассимиляцией или пластическим обменом. В ходе ассимиляции обновляются органоиды клетки и накапливается запас энергии. Распад структурных элементов клетки сопровождается выделением заключенной в химических связях энергии, а конечные продукты распада, вредные для организма, выводятся за пределы клетки и затем из организма.

Процесс распада органических веществ противоположен процессу ассимиляции и называется диссимиляцией. Подобного типа реакции идут с поглощением кислорода, поэтому расщепление органических веществ связано с окислением, а освобождающаяся при этом энергия идет на синтез АТФ, необходимой для ассимиляции.

Таким образом, ассимиляция и диссимиляция - это две противоположные, но взаимно связанные стороны единого процесса - обмена веществ. При нарушении ассимиляции и диссимиляции расстраивается весь обмен веществ. Непрерывный распад и окисление органических соединений возможны лишь тогда, когда количество этих веществ в клетках постоянно пополняется. Поэтому при разработке пищевых норм учитываются калорийность пищевых продуктов: белков, жиров, углеводов с тем расчетом, чтобы расход энергии не превышал потребления.

В неживой природе обменные процессы затухают, поскольку отдавая «большее», природа получает «меньшее», что обусловливает явление энтропии и регрессивную эволюцию. В живой природе и в обществе тот же самый процесс обмена выглядит иначе. Здесь ситуация такова, что отдавая «меньшее» необходимо получать «большее». Отсюда следует противоположный энтропии процесс, обусловливающий прогрессивную эволюцию[10].

Список литературы:

1.     Войткович Г.В. Происхождение и химическая эволюция солнечной системы. М.: Наука, 1991.

2.     Волькенштейн М.В. Энтропия и информация. М.: Наука, 1986.

3.     Девис П. Суперсила – М.: Мир, 1989.

4.     Дубнищева Т.Я. Концепции современного естествознания. Новосибирск: ООО «Издательство ЮКЭА», 2000.

5.     Дубнищева Т.Я., Пигарев А.Ю. Современное естествознание. Новосибирск: ООО «Издательство ЮКЭА», 2000.

6.     Моисеев Н. Экология человечества глазами математика. М.: Молодая гвардия, 1988.

7.     Мурахвери В. Поляризованный свет в природе. М.: Знание, 1971.

8.     Рубин А.Б. Термодинамика биологических процессов. М.: Изд-во МГУ, 1984.

9.     Яблоков А.В. Актуальные проблемы эволюционной теории. М.: Наука, 1966.

[1] Яблоков А.В. Актуальные проблемы эволюционной теории. М.: Наука, 1966. С.67-69.

[2] Дубнищева Т.Я. Концепции современного естествознания. Новосибирск: ООО «Издательство ЮКЭА», 2000. С. 92.

[3] Мурахвери В. Поляризованный свет в природе. М.: Знание, 1971. С. 199.

[4] Дубнищева Т.Я., Пигарев А.Ю. Современное естествознание. Новосибирск: ООО «Издательство ЮКЭА», 1998. С. 32.

[5] Дубнищева Т.Я., Пигарев А.Ю. Современное естествознание. Новосибирск: ООО «Издательство ЮКЭА», 2000. С.37-42.

[6] Рубин А.Б. Термодинамика биологических процессов. М.: Изд-во МГУ, 1984. С. 280.

[7] Войткович Г.В. Происхождение и химическая эволюция солнечной системы. М.: Наука, 1991. С. 110-112.

[8] Моисеев Н. Экология человечества глазами математика. М.: Молодая гвардия, 1988. С.55-59.

[9] Дубнищева Т.Я., Пигарев А.Ю. Современное естествознание. Новосибирск: ООО «Издательство ЮКЭА», 2000. С.80-82.

[10] Волькенштейн М.В. Энтропия и информация. М.: Наука, 1986. С. 90-92.