ВАРИАНТ 1
Содержание
Задача 1. 3
3адача 2. 3
Задача 3. 9
Задача 4. 12
Задача 5. 16
Задача 6. 19
Задача 7. 22
Задача 8. 24
Задача 9. 28
Задача 1
В приложении А приведены данные о выпуске товаров и услуг малыми предприятиями одной из отраслей экономики региона. Используя таблицу случайных чисел или их генератор, включенный в различные статистические (математические) пакеты программ обработки данных на ПЭВМ, сформируйте массив случайных чисел и произведите 30-процентную простую случайную бесповторную выборку.
По выборочным данным:
1. Постройте интервальный ряд распределения, образовав пять групп с равными интервалами.
2. Исчислите средний объем выпуска товаров и услуг, приходящийся на одно предприятие, а также долю предприятий с объемом выпуска товаров и услуг, более 40 млн руб.
3. С вероятностью 0,954 определите доверительные интервалы, в которых можно ожидать генеральные параметры: а) средний размер выпуска товаров и услуг одного предприятия; б) долю малых предприятий с объемом выпуска товаров и услуг более 40 млн руб.; в) общий объем выпуска товаров и услуг малыми предприятиями региона, г) число предприятий с объемом выпуска товаров и услуг более 40 млн руб.
Подтвердите достоверность полученных оценок расчетом генеральных характеристик.
Сделайте выводы.
Решение
Используя 1-й столбец таблицы случайных чисел сформируем 30 – элементный массив неповторяющихся случайных чисел и произведем соответствующую простую случайную бесповторную выборку:
|
№ |
Случ.число (№ предприятия) |
Выпуск товаров и услуг (млн. руб) |
|
1 |
54 |
44 |
|
2 |
89 |
51 |
|
3 |
35 |
17 |
|
4 |
22 |
41 |
|
5 |
75 |
32 |
|
6 |
55 |
45 |
|
7 |
57 |
25 |
|
8 |
59 |
4 |
|
9 |
63 |
24 |
|
10 |
3 |
5 |
|
11 |
73 |
39 |
|
12 |
51 |
14 |
|
13 |
70 |
10 |
|
14 |
68 |
4 |
|
15 |
36 |
3 |
|
16 |
13 |
12 |
|
17 |
43 |
38 |
|
18 |
98 |
8 |
|
19 |
15 |
9 |
|
20 |
80 |
3 |
|
21 |
11 |
8 |
|
22 |
87 |
7 |
|
23 |
41 |
2 |
|
24 |
84 |
15 |
|
25 |
29 |
19 |
|
26 |
16 |
1 |
|
27 |
24 |
29 |
|
28 |
1 |
40 |
|
29 |
46 |
4 |
|
30 |
49 |
2 |
|
Итого |
|
555 |
1. Строим ранжированный ряд предприятий по выпуску товаров и услуг:
|
Ранг |
Выпуск товаров и услуг (млн. руб) |
№ предприятия |
|
1 |
1 |
1 |
|
2 |
2 |
2 |
|
3 |
3 |
2 |
|
4 |
4 |
3 |
|
5 |
5 |
3 |
|
6 |
6 |
4 |
|
7 |
7 |
4 |
|
8 |
8 |
4 |
|
9 |
9 |
5 |
|
10 |
10 |
7 |
|
11 |
11 |
8 |
|
12 |
12 |
8 |
|
13 |
13 |
9 |
|
14 |
14 |
10 |
|
15 |
15 |
12 |
|
16 |
16 |
14 |
|
17 |
17 |
15 |
|
18 |
18 |
17 |
|
19 |
19 |
19 |
|
20 |
20 |
24 |
|
21 |
21 |
25 |
|
22 |
22 |
29 |
|
23 |
23 |
32 |
|
24 |
24 |
38 |
|
25 |
25 |
39 |
|
26 |
26 |
40 |
|
27 |
27 |
41 |
|
28 |
28 |
44 |
|
29 |
29 |
45 |
|
30 |
30 |
51 |
При n=5 получаем
размер интервала ![]() =(51 –1)/5=10
=(51 –1)/5=10
|
№ интервала |
Левая граница |
Правая граница |
Ранги точек интервала |
|
1-й интервал |
1 |
11 |
1 – 14 |
|
2-й интервал |
11 |
21 |
15 – 19 |
|
3-й интервал |
21 |
31 |
20 –22 |
|
4-й интервал |
31 |
41 |
23 – 27 |
|
5-й интервал |
41 |
51 |
28 - 30 |
Получаем интервальный ряд распределения:
|
Выпуск товаров и услуг (млн. руб) |
Частота |
Частость, % |
|
1 – 11 |
14 |
46,67 |
|
11 –21 |
5 |
16,67 |
|
21 – 31 |
3 |
10 |
|
31 – 41 |
5 |
16,67 |
|
41 - 51 |
3 |
10 |
|
Итого |
30 |
100 |
2. Средний объем выпуска товаров и услуг, приходящийся на одно предприятие:
![]() =555/30=18,5
=555/30=18,5
Доля предприятий с объемом выпуска товаров и услуг, более 40 млн руб.:
![]()
3. Так как вероятность ошибки равна 0,954, то уровень
коэффициента доверия ![]() .
.
а) средний размер выпуска товаров и услуг одного предприятия находится в интервале:
![]() , где
, где ![]()
Выборочная дисперсия: ![]() . Для вычисления составляем вспомогательную таблицу:
. Для вычисления составляем вспомогательную таблицу:
|
№ |
№ предприятия |
Выпуск товаров и услуг (млн. руб |
|
|
|
1 |
54 |
44 |
25,500 |
650,250 |
|
2 |
89 |
51 |
32,500 |
1056,250 |
|
3 |
35 |
17 |
-1,500 |
2,250 |
|
4 |
22 |
41 |
22,500 |
506,250 |
|
5 |
75 |
32 |
13,500 |
182,250 |
|
6 |
55 |
45 |
26,500 |
702,250 |
|
7 |
57 |
25 |
6,500 |
42,250 |
|
8 |
59 |
4 |
-14,500 |
210,250 |
|
9 |
63 |
24 |
5,500 |
30,250 |
|
10 |
3 |
5 |
-13,500 |
182,250 |
|
11 |
73 |
39 |
20,500 |
420,250 |
|
12 |
51 |
14 |
-4,500 |
20,250 |
|
13 |
70 |
10 |
-8,500 |
72,250 |
|
14 |
68 |
4 |
-14,500 |
210,250 |
|
15 |
36 |
3 |
-15,500 |
240,250 |
|
16 |
13 |
12 |
-6,500 |
42,250 |
|
17 |
43 |
38 |
19,500 |
380,250 |
|
18 |
98 |
8 |
-10,500 |
110,250 |
|
19 |
15 |
9 |
-9,500 |
90,250 |
|
20 |
80 |
3 |
-15,500 |
240,250 |
|
21 |
11 |
8 |
-10,500 |
110,250 |
|
22 |
87 |
7 |
-11,500 |
132,250 |
|
23 |
41 |
2 |
-16,500 |
272,250 |
|
24 |
84 |
15 |
-3,500 |
12,250 |
|
25 |
29 |
19 |
0,500 |
0,250 |
|
26 |
16 |
1 |
-17,500 |
306,250 |
|
27 |
24 |
29 |
10,500 |
110,250 |
|
28 |
1 |
40 |
21,500 |
462,250 |
|
29 |
46 |
4 |
-14,500 |
210,250 |
|
30 |
49 |
2 |
-16,500 |
272,250 |
|
сумма |
|
555 |
|
7279,5 |
Получаем: ![]() ,
, ![]()
Доверительный интервал для среднего
размера выпуска товаров и услуг одного предприятия: ![]() ,
,
![]()
Для генеральной совокупности ![]() принадлежит
доверительному интервалу.
принадлежит
доверительному интервалу.
б) Доля малых предприятий с объемом выпуска товаров и
услуг более 40 млн. руб. находится в интервале: ![]() , где
, где 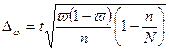 .
.
Получаем: 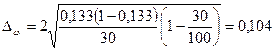 .
.
Доверительный интервал для доли малых предприятий с
объемом выпуска товаров и услуг более 40 млн. руб.: ![]() ,
,
![]() .
.
Для генеральной совокупности ![]() принадлежит
доверительному интервалу.
принадлежит
доверительному интервалу.
в) Общий объем выпуска товаров и
услуг 100 малыми предприятиями региона находится в интервале: ![]() .
.
Для генеральной совокупности ![]() принадлежит
доверительному интервалу.
принадлежит
доверительному интервалу.
г) Число предприятий с объемом выпуска товаров и услуг
более 40 млн руб. находится в интервале: ![]() .
.
Для генеральной совокупности ![]() принадлежит
доверительному интервалу.
принадлежит
доверительному интервалу.
Выводы.
Средний объем выпуска товаров и услуг, приходящийся на одно предприятие равен18,5.
Доля предприятий с объемом выпуска товаров и услуг, более 40 млн руб равна 0,133.
Доверительный интервал для среднего
размера выпуска товаров и услуг одного предприятия:![]() Для генеральной
совокупности
Для генеральной
совокупности ![]() принадлежит доверительному
интервалу.
принадлежит доверительному
интервалу.
Доверительный интервал для доли
малых предприятий с объемом выпуска товаров и услуг более 40 млн. руб.: ![]() Для генеральной совокупности
Для генеральной совокупности ![]() принадлежит
доверительному интервалу.
принадлежит
доверительному интервалу.
3адача 2
На основе 5-процентной пропорциональной расслоенной (типической) выборки со случайным отбором единиц в слое получены сведения о вкладах населения района области. Результаты выборочного наблюдения обобщены в таблице:
|
Типы населения |
Число вкладов, тыс. ед. |
Средний размер вклада, тыс.руб. |
Коэффициент вариации вкладов, % |
|
Городское |
30 |
7 |
15 |
|
Сельское |
20 |
5 |
21 |
Определите:
1) тесноту связи между типом населения и средним размером вклада, исчислив эмпирическое корреляционное отношение;
2) с вероятностью 0,954 доверительные интервалы, в которых можно ожидать: а) средний размер вклада всего населения района области; б) общую сумму вкладов населения района;
3) как изменится точность средней и предельной ошибок выборки, если предположить, что приведенные данные получены в результате простой случайной бесповторной выборки.
Сделайте выводы.
Решение
1) Вычисляем эмпирическое корреляционное отношение по формуле: ![]() , где
, где
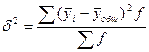 - межгрупповая дисперсия;
- межгрупповая дисперсия;
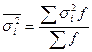 - внутригрупповая
дисперсия;
- внутригрупповая
дисперсия;
![]() - общая дисперсия
результативного признака.
- общая дисперсия
результативного признака.
Дисперсии в
отдельных группах находим из формулы коэффициента
вариации успеваемости студентов: ![]() .
.
Составляем вспомогательную таблицу:
|
Типы населения |
Число вкладов, тыс. ед. fi |
Средний размер вклада, тыс.руб. yi |
|
|
|
|
|
|
|
Городское |
30 |
7 |
15 |
210 |
0,64 |
19,2 |
1,05 |
33,075 |
|
Сельское |
20 |
5 |
21 |
100 |
1,44 |
28,8 |
1,05 |
22,05 |
|
Итого |
50 |
|
|
310 |
|
48 |
|
55,125 |
Находим 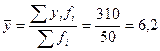
Находим
межгрупповую дисперсию: ![]() .
.
Находим
внутригрупповую дисперсию: ![]()
Находим общую дисперсию: ![]()
Вычисляем эмпирическое корреляционное отношение: ![]() .
.
Так как эмпирическое корреляционное отношение близко к 0,5, то между типом населения и средним размером вклада существует умеренная связь.
2) Так как
вероятность ошибки равна 0,954, то уровень коэффициента доверия ![]() .
.
Величина среднего размера вклада находится в интервале: ![]() , где
, где ![]() . Получаем:
. Получаем: ![]()
Доверительный интервал, в котором можно ожидать
величину среднего размера вклада
![]()
![]() .
.
3) Если предположить, что приведенные данные получены в результате простой случайной бесповторной выборки, то точность средней и предельной ошибок выборки будет более высокой.
Вывод: Между типом населения и средним
размером вклада существует
умеренная связь. С вероятностью 0,954 величина среднего размера вклада
находится в интервале: ![]()
Задача 3
По субъекту Российской Федерации имеются следующие данные:
|
Показатель |
2002 г. |
2002 г.в % к 2000 г. |
|
Экспорт, млн.USD - всего |
2708,5 |
|
|
в том числе: |
|
|
|
в страны вне СНГ |
2306,3 |
120,3 |
|
в страны СНГ |
402,2 |
80,3 |
|
Импорт , млн.USD - всего |
1077,4 |
|
|
В том числе: |
|
|
|
из стран вне СНГ |
524,4 |
103,3 |
|
из стран СНГ |
548 |
102,6 |
Определите:
1) недостающие элементы таблицы;
2) географическую структуру экспорта и импорта в 2000 и 2002 гг.;
3) для оценки тесноты связи между направлением товаропотока и географическим распределением внешнеторгового оборота за каждый год коэффициенты ассоциации и контингенции.
Сделайте выводы.
Решение
Для нахождения недостающих элементов таблицы найдем абсолютные показатели 2000 г.
|
Показатель |
2002 г. |
2002 г.в % к 2000 г. |
2000 г. |
|
Экспорт, млн.USD - всего |
2708,5 |
112 |
1917,1+500,9=2418 |
|
в том числе: |
|
|
|
|
в страны вне СНГ |
2306,3 |
120,3 |
2306,3/1,203 =1917,1 |
|
в страны СНГ |
402,2 |
80,3 |
402,2/ 0,803=500,9 |
|
Импорт , млн.USD - всего |
1077,4 |
102,9 |
512,5+534,1=1046,6 |
|
В том числе: |
|
|
|
|
из стран вне СНГ |
529,4 |
103,3 |
529,4/1,033=512,5 |
|
из стран СНГ |
548 |
102,6 |
548/ 1,026=534,1 |
Расчетная таблица для 2000 г.:
|
2000 г. |
страны вне СНГ |
страны СНГ |
Всего |
|
Экспорт |
1917,1 (a) |
500,9 (b) |
2418 (a+b) |
|
Импорт |
512,5 (c) |
534,1 (d) |
1046,6 (c+d) |
|
Итого |
2429,6(a+c) |
1035 (b+d) |
3464,6 |
Расчетная таблица для 2002 г.:
|
2000 г. |
страны вне СНГ |
страны СНГ |
Всего |
|
Экспорт |
2306,3 (a) |
402,2 (b) |
2708,5 (a+b) |
|
Импорт |
529,4 (c) |
548 (d) |
1077,4 (c+d) |
|
Итого |
2835,7 (a+c) |
950,2 (b+d) |
3785,9 |
Коэффициент
ассоциации находим по формуле: ![]()
Коэффициент
контингенции: находим по формуле: ![]()
2000г:
Коэффициент
ассоциации: ![]() .
.
Коэффициент
контингенции: ![]() .
.
2002 г.
Коэффициент
ассоциации:![]() .
.
Коэффициент
контингенции: ![]() .
.
Вывод. Рассчитанные коэффициенты свидетельствуют о незначительной связи между направлением товаропотока и географическим распределением внешнеторгового оборота. Связь между направлением товаропотока и географическим распределением внешнеторгового оборота выше в 2002 г.
Задача 4
Имеются данные об экспорте филе рыбного:
|
|
Базисный период |
Отчетный период |
||
|
Количество, т |
Стоимость, тыс.USD |
Количество, т |
Стоимость, тыс.USD |
|
|
Экспорт – всего в том числе в страны: |
497 |
1483 |
491 |
1567 |
|
А |
18 |
77 |
53 |
265 |
|
Б |
262 |
907 |
410 |
1186 |
|
В |
178 |
419 |
8 |
30 |
|
Г |
- |
- |
20 |
86 |
|
Д |
39 |
80 |
- |
- |
Определите:
I. По группе сопоставимых стран импортеров:
1) для оценки структурных изменений, произошедших в географическом распределении товаропотока. интегральный коэффициент структурных сдвигов К. Гатева;
2) динамику средней цены 1 т поставленного на экспорт филе рыбного;
3) в какой мере эта динамика была обусловлена:
а) изменением цены 1т экспортированного филе рыбного в каждую из стран;
б) изменением квот на экспорт филе рыбного в страны.
II. По всем странам импортерам:
динамику средней цены 1т поставленного на экспорт филе рыбного.
Сделайте выводы.
Решение
I. Интегральный коэффициент К.
Гатева находим по формуле: 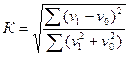 , где
, где ![]() - доли стран в общем
объеме экспорта в отчетном и базисном периодах.
- доли стран в общем
объеме экспорта в отчетном и базисном периодах.
Составляем расчетную таблицу:
|
Экспорт в страны |
Стоимость в базисном периоде
|
Стоимость в отчетном периоде
|
|
|
|
|
|
А |
77 |
265 |
0,055 |
0,178 |
0,015 |
0,035 |
|
Б |
907 |
1186 |
0,646 |
0,799 |
0,023 |
1,055 |
|
В |
419 |
30 |
0,298 |
0,020 |
0,077 |
0,089 |
|
Всего |
1405 |
1485 |
0,999 |
0,997 |
0,116 |
1,179 |
Получаем: ![]() .
.
Так как интегральный коэффициент структурных сдвигов К. Гатева близок к 0, то структурные изменения, произошедших в географическом распределении товаропотока незначительны.
2) По группе сопоставимых стран импортеров (А, Б, В) составляем расчетную таблицу:
|
Экспорт в страны |
Базисный период |
Отчетный период |
Цена в базис- ном пери- оде |
Цена в отчет- ном пери- оде |
|
Дина- мика цен |
||
|
Коли- чество
|
Стои- мость
|
Коли- чество
|
Стои- мость
|
|||||
|
|
1 |
2 |
3 |
4 |
5=2/1 |
6=4/2 |
7=5*3 |
(6/5-1)*100% |
|
А |
18 |
77 |
53 |
265 |
4,278 |
5,000 |
226,722 |
16,883 |
|
Б |
262 |
907 |
410 |
1186 |
3,462 |
2,893 |
1419,351 |
-16,441 |
|
В |
178 |
419 |
8 |
30 |
2,354 |
3,750 |
18,831 |
59,308 |
|
Всего |
459 |
1405 |
474 |
1485 |
3,061 |
3,133 |
1450,915 |
2,349 |
Средняя цена1 т поставленного на экспорт филе рыбного увеличилась на
3,133 – 3,061=0,072 USD, т.е. на 2,349%.
3) а) Индекс фиксированнного состава:
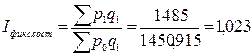
Средняя цена1 т поставленного на экспорт филе рыбного увеличилась на 2,3% из-за изменения цены 1т экспортированного филе рыбного в каждую из стран.
б) Индекс структурных сдвигов: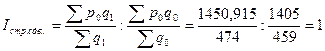 .
.
Изменение квот на экспорт филе рыбного в страны не повлияло на динамику средней цены1 т поставленного на экспорт филе рыбного.
II. Составляем расчетную таблицу по всем странам импортерам:
|
Экспорт в страны |
Базисный период |
Отчетный период |
Цена в базис- ном пери- оде |
Цена в отчет- ном пери- оде |
|
Дина- мика цен |
||
|
Коли- чество
|
Стои- мость
|
Коли- чество
|
Стои- мость
|
|||||
|
|
1 |
2 |
3 |
4 |
5=2/1 |
6=4/3 |
7=5*3 |
(6/5-1)*100% |
|
А |
18 |
77 |
53 |
265 |
4,278 |
5,000 |
226,722 |
16,883 |
|
Б |
262 |
907 |
410 |
1186 |
3,462 |
2,893 |
1419,351 |
-16,441 |
|
В |
178 |
419 |
8 |
30 |
2,354 |
3,750 |
18,831 |
59,308 |
|
Г |
0 |
0 |
20 |
86 |
|
4,300 |
0,000 |
|
|
Д |
39 |
80 |
0 |
0 |
2,051 |
|
0,000 |
|
|
Всего |
497 |
1483 |
491 |
1567 |
2,984 |
3,191 |
1465,097 |
6,955 |
По всем странам импортерам средняя цена1 т поставленного на экспорт филе рыбного увеличилась на 3,191 – 2,984=0,207 USD, т.е. на 6,955%.
Выводы:
По группе сопоставимых стран импортеров структурные изменения, произошедшие в географическом распределении товаропотока незначительны.
Средняя цена1 т поставленного на экспорт филе рыбного увеличилась на 2,349%, это изменение произошло только из-за изменения цены 1т экспортированного филе рыбного в каждую из стран. Изменение квот на экспорт филе рыбного в страны не повлияло на динамику средней цены.
По всем странам импортерам средняя цена1 т поставленного на экспорт филе рыбного увеличилась на 6,955%.
Задача 5
Имеются следующие данные о продаже сельскохозяйственной продукции в январе отчетного года на городском рынке обследованного региона:
|
Виды продуктов |
Продано |
Средние цены |
||
|
тонн. |
в % к январю базисного года |
У.е. за кг |
в % к январю базисного года |
|
|
А |
3,3 |
87 |
5,32 |
106 |
|
В |
0,4 |
88 |
4,84 |
104 |
|
С |
2,1 |
113 |
4,07 |
96 |
Определите:
1) средний арифметический индекс физического объема оборота розничной торговли, общие индексы цен Э.Ласпейреса и Г Пааше, а также их аналогии в средней арифметической и гармонической форме, общий индекс оборота розничной торговли.
2) общее (абсолютное) изменение оборота розничной торговли - всего и в том числе за счет изменений: а) физического объема продаж товаров; б) цен на товары.
Сделайте выводы.
Решение
Пусть
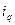 -индивидуальный
индекс физического объема проданной
продукции,
-индивидуальный
индекс физического объема проданной
продукции,
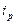 - индивидуальный
индекс цен.
- индивидуальный
индекс цен.
Составляем вспомогательную таблицу:
|
Виды про-дук- тов |
Продано |
Цена |
|
|
Стоимость |
|
|
|||
|
Базис-ный пери-од
|
Отчет- ный пери- од
|
Базис-ный пери-од
|
Отчет- ный пери- од
|
Базис-ный пери-од
|
Отчет- ный пери- од
|
|||||
|
|
1 |
2=1*5 |
3 |
4=3*6 |
5 |
6 |
7=3*1 |
6=4*2 |
7=2*3 |
8=1*4 |
|
А |
3,3 |
2,871 |
5,320 |
5,639 |
0,870 |
1,060 |
17,556 |
16,190 |
15,274 |
18,609 |
|
Б |
0,4 |
0,352 |
4,840 |
5,034 |
0,880 |
1,040 |
1,936 |
1,772 |
1,704 |
2,013 |
|
В |
2,1 |
2,373 |
4,070 |
3,907 |
1,130 |
0,960 |
8,547 |
9,272 |
9,658 |
8,205 |
|
Всего |
6,8 |
5,596 |
|
|
|
|
28,039 |
27,234 |
26,636 |
28,828 |
1)
Средний арифметический индекс физического объема оборота
розничной торговли: 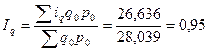 .
.
Общий индекс цен
Э.Ласпейреса: 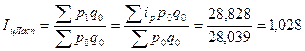
Общий индекс цен Г.
Пааше: 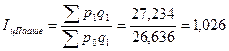
Общий индекс оборота
розничной торговли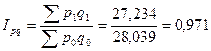
2) Общее (абсолютное) изменение оборота розничной торговли: ![]() - оборот розничной торговли уменьшился на 0,805
- оборот розничной торговли уменьшился на 0,805
а) За счет
изменений цен: ![]() оборот розничной торговли увеличился на 0,598.
оборот розничной торговли увеличился на 0,598.
б) За счет изменений физического объема оборота
розничной торговли: ![]() оборот розничной торговли уменьшился на 1,403.
оборот розничной торговли уменьшился на 1,403.
Вывод. Оборот розничной торговли уменьшился на 0,805 (2,9%). Физический объем оборота розничной торговли уменьшился на 5%. За счет изменений цен оборот розничной торговли уменьшился на 0,598. За счет изменений физического объема оборот розничной торговли увеличился на 1,403.
Задача 6
Численность населения города на конец года составила 700 тыс. чел. Известно, что в течение года в городе родилось 10, а умерло 12 тыс. чел., в том числе детей в возрасте до 1 года – 200 чел. В анализируемом году выявлено положительное сальдо миграции, равное 12 тыс. чел.
Справочно: удельный вес женщин в возрасте 15-49 лет в общей среднегодовой численности населения города составил 30 %.
Определите: а) численность населения города на начало года; б) среднегодовую численность населения города; в) общий и специальный коэффициент рождаемости, коэффициент жизненности; г) общий коэффициент смертности; д) коэффициенты естественного прироста и миграции населения; е) коэффициенты жизненности, оборота и экономичности воспроизводства населения.
Сделайте выводы.
Решение
По условию:
![]() тыс.
чел -
численность населения на конец года;
тыс.
чел -
численность населения на конец года;
![]() =10 тыс. чел - число родившихся за год;
=10 тыс. чел - число родившихся за год;
![]() =12 тыс. чел –
число умерших за год;
=12 тыс. чел –
число умерших за год;
![]() =
0,2 тыс. чел –
число умерших за год детей в возрасте до 1 года;
=
0,2 тыс. чел –
число умерших за год детей в возрасте до 1 года;
![]() =12 тыс. чел - сальдо миграции;
=12 тыс. чел - сальдо миграции;
![]() - доля женщин в возрасте 15-49 лет в общей среднегодовой
численности населения.
- доля женщин в возрасте 15-49 лет в общей среднегодовой
численности населения.
а)
Численность населения города на начало года находится из формулы: ![]() . Получаем
. Получаем ![]() =690 тыс. чел.
=690 тыс. чел.
б)
Среднегодовая численность населения
города ![]() =695 тыс. чел.
=695 тыс. чел.
в)
Общий коэффициент рождаемости![]() =14,388.
=14,388.
Специальный
коэффициент рождаемости![]()
Коэффициент
жизненности ![]()
г)
Общий коэффициент смертности ![]()
д)
Коэффициент
естественного прироста ![]()
Коэффициент
миграции населения ![]() = 17,266.
= 17,266.
е) Коэффициент оборота населения ![]() = 14,388+17,266=31,654.
= 14,388+17,266=31,654.
Коэффициент экономичности воспроизводства населения ![]() =
=
-2,928/31,654 = 0,093.
Задача 7
По одной из организаций региона за отчетный год имеются следующие данные:
1. Организация зарегистрирована и действует с 20 октября. Численность работников ее списочного состава в октябре составляла: 20 октября (понедельник) -315 чел., 21 октября (вторник) - 305 чел., 22 октября (среда) - 3]7 чел., 23 октября (четверг) - 320 чел., 24 октября (пятница) — 335 чел., 25 и 26 октября — выходные дни, 27 октября — 334 чел., 28 октября - 330 чел., 29 октября-325 чел., 30 октября - 310 чел., 31 октябри -307 чел.
Кроме того, известно, что численность совместителей с 20 по 27 октября составила 70 чел., с 28 по 31 октября - 85 чел,- а число работающих по договорам гражданско-правового характера, зарегистрировано с 20 по 23 октября 15 чел., с 24 по 31 октября - 10 чел.
2. В ноябре число явок на работу зарегистрировано 5859 человеко-дней, число неявок по всем причинам 3891 человеко-дней.
3. Среднесписочная численность работников за декабрь составила 320 чел.
Определите:
1) за октябрь а) среднюю численность внешних совместителей; б) среднюю численность работников, выполнявших работу по договорам гражданско-правового характера;
2) среднесписочную численность работников организации за год.
Решение
Среднесписочную численность работников
организации находим по формуле: ![]() , где
, где ![]() - списочная
численность на t-й день,
включая совместителей;
- списочная
численность на t-й день,
включая совместителей;
N – количество календарных дней в периоде.
1) В октябре:
а) Средняя численность внешних совместителей равна ![]()
б) Средняя численность работников, выполнявших работу по договорам
гражданско-правового характера равна ![]() .
.
2) Период с 20 октября до конца года состоит из 12+30+31=73 дней.
![]() =315+305+ 3]7+
320+335+334+330+325+310+307+8*70+4*85=4098.
=315+305+ 3]7+
320+335+334+330+325+310+307+8*70+4*85=4098.
![]() = 5859+3891 = 9750.
= 5859+3891 = 9750.
![]() =31*320=9920.
=31*320=9920.
Среднесписочная численность работников организации за год:
![]() .
.
Задача 8
По субъекту Федерации имеются следующие данные, млрд руб.:
|
Основные фонды по полной восстановительной стоимости на начало года |
300 |
|
Степень износа основных фондов на начало года, % |
30 |
|
Введено новых основных фондов за год |
50 |
|
Выбыло основных фондов по полной стоимости |
30 |
|
Остаточная стоимость выбывших основных фондов |
45 |
|
Сумма начисленного износа за год |
25 |
|
Затраты на капитальный ремонт за год |
18 |
Определите:
1) полную восстановительную стоимость на конец года;
2) восстановительную стоимость за вычетом износа на начало и конец года;
3) коэффициенты годности основных фондов на начало и конец года;
4) коэффициент износа основных фондов на конец года;
коэффициенты обновления и выбытия основных фондов.
Постройте балансы основных фондов по полной восстановительной стоимости и восстановительной стоимости за вычетом износа.
Сделайте выводы.
Решение.
Введем обозначения для исходных данных:
|
Основные фонды по полной восстановительной стоимости на начало года (Фн) |
300 |
|
Степень износа основных фондов на начало года, % (Кизн,н.г.) |
30 |
|
Введено новых основных фондов за год (П) |
50 |
|
Выбыло основных фондов по полной стоимости (В) |
30 |
|
Остаточная стоимость выбывших основных фондов В*) |
45 |
|
Сумма начисленного износа за год (Ик) |
25 |
|
Затраты на капитальный ремонт за год (Р) |
18 |
1. Полная восстановительная стоимость основных средств на конец года:
Фк = Фн +П –В = 300 + 50 – 30 = 320.
2. Восстановительная стоимость за вычетом износа на начало года
Он = 300*(100-30)/100=210
Восстановительная стоимость за вычетом износа на конец года
Ок = Он + П – В* - Ик - Р = 172.
3.Коэффициент годности на начало года Кгодности н.г. = Он / Фн *100 =210/300 *100= 70%.
Коэффициент годности на конец года Кгодности к.г.= Ок / Фк *100=172 /320 *100 = 53,75%.
4. Коэффициент износа на конец года Кизн,к.г.= 100 - Кгодности к.г. =100 – 53,75 =29,9 %.
5. Коэффициент обновления Кобнов = П / Фк *100 = 50/ 320 * 100 = 15,6%.
Коэффициент выбытия: Квыб = В / Фн 100 = 30/320*100 = 9,4%.
Задача 9
За отчетный период имеются данные о распределении домохозяйств региона по размеру среднедушевых денежных доходов:
|
Среднедушевой денежный доход, руб |
Число домохозяйств,% |
Численность населения, % |
|
До 800 |
6,5 |
7,5 |
|
800-1200 |
29,3 |
23,4 |
|
1200-1600 |
21,6 |
21,7 |
|
1600-2000 |
11,4 |
13,5 |
|
2000-2400 |
9,1 |
8,4 |
|
2400-2800 |
8,3 |
7,3 |
|
2800-3200 |
7 |
6,7 |
|
3200-3600| |
3,1 |
2,5 |
|
3600 и более |
3,7 |
9 |
|
Итого |
100 |
100 |
Справочно: общее число домохозяйств в регионе составляет 806,5 тыс. Одно домохозяйство в среднем состоит из 3,2 лица.
Определите:
1. Среднедушевой месячный доход населения региона.
2. Модальные и медианные размеры среднедушевых месячных доходов населения региона.
3. Показатели дифференциации и концентрации доходов населения региона: а) децильный коэффициент; б) коэффициент К.Джини; в) коэффициент Херфиндаля-Хиршмана.
4. Численность населения региона, имеющего доход ниже прожиточного минимума, установленного в отчетном периоде в размере 1530 руб.
5. Уровень бедности к регионе.Постройте кривую М. Лоренца.
Сделайте выводы об уровне и динамике доходов населения региона и их концентрации.
Решение.
Вычисляем численность населения в каждой группе по числу домохозяйств и по численности населения и составляем таблицу:
|
Средне- душевой денежный доход, руб. |
Середина интервала
|
Численность населения по числу домохозяйств
|
Численность населения
|
|
|
|
До 800 |
600 |
167,8 |
193,6 |
100651,2 |
116136 |
|
800-1200 |
1000 |
756,2 |
603,9 |
756174,4 |
603907,2 |
|
1200-1600 |
1400 |
557,5 |
560,0 |
780433,9 |
784047,04 |
|
1600-2000 |
1800 |
294,2 |
348,4 |
529580,2 |
627134,4 |
|
2000-2400 |
2200 |
234,9 |
216,8 |
516676,2 |
476931,84 |
|
2400-2800 |
2600 |
214,2 |
188,4 |
556936,6 |
489835,84 |
|
2800-3200 |
3000 |
180,7 |
172,9 |
541968 |
518740,8 |
|
3200-3600| |
3400 |
80,0 |
64,5 |
272016,3 |
219368 |
|
3600 и более |
3800 |
95,5 |
232,3 |
362860,5 |
882633,6 |
|
Итого |
|
2580,8 |
2580,8 |
4417297 |
4718734,72 |
1.
Среднедушевой месячный доход населения региона, рассчитанный по числу домохозяйств равен 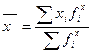 =1711,6.
=1711,6.
Среднедушевой
месячный доход населения региона, рассчитанный
по численности населения равен 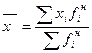 =2243,8.
=2243,8.
2.
Мода и медиана определяются по формулам: 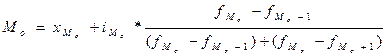 ,
, 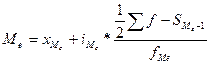 .
.
Модальным по числу домохозяйств является интервал [800;1200]. Получаем:
![]()
Модальным по численности населения является интервал [800;1200]. Получаем:
![]() .
.
Медианным интервалом по числу домохозяйств является интервал [1200 -
1600], содержащий ![]() - тыс чел. Получаем:
- тыс чел. Получаем:  = 1553,84.
= 1553,84.
Медианным интервалом по
численности населения является интервал [1200 - 1600], содержащий ![]() - тыс чел. Получаем:
- тыс чел. Получаем: 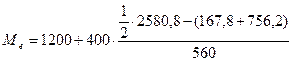 = 1552,07.
= 1552,07.
3. а) Децильный коэффициент равен отношению максимального денежного дохода у 10 процентов наименее и минимального денежного дохода у 10 процентов наиболее обеспеченного населения.
Децильный коэффициент, рассчитанный по числу домохозяйств равен 1200/2800= 0,428
Децильный коэффициент, рассчитанный по численности населения равен 1200/3200= 0,375
б)
Коэффициент К.Джини находим по формуле: ![]() ,
,
где ![]() - доля i-й группы в объеме совокупности,
- доля i-й группы в объеме совокупности, ![]() - доля i-й группы в общем объеме доходов,
- доля i-й группы в общем объеме доходов, ![]() - накопленная доля i-й группы в общем объеме доходов.
- накопленная доля i-й группы в общем объеме доходов.
Составляем вспомогательную таблицу по числу домохозяйств:
|
|
|
|
|
|
|
|
|
|
|
600 |
167,752 |
100651,2 |
0,065 |
0,0228 |
0,0228 |
0,0015 |
0,0015 |
0,0042 |
|
1000 |
756,1744 |
756174,4 |
0,293 |
0,1712 |
0,1940 |
0,0502 |
0,0568 |
0,0858 |
|
1400 |
557,4528 |
780433,9 |
0,216 |
0,1767 |
0,3706 |
0,0382 |
0,0801 |
0,0467 |
|
1800 |
294,2112 |
529580,2 |
0,114 |
0,1199 |
0,4905 |
0,0137 |
0,0559 |
0,0130 |
|
2200 |
234,8528 |
516676,2 |
0,091 |
0,1170 |
0,6075 |
0,0106 |
0,0553 |
0,0083 |
|
2600 |
214,2064 |
556936,6 |
0,083 |
0,1261 |
0,7336 |
0,0105 |
0,0609 |
0,0069 |
|
3000 |
180,656 |
541968 |
0,070 |
0,1227 |
0,8563 |
0,0086 |
0,0599 |
0,0049 |
|
3400 |
80,0048 |
272016,3 |
0,031 |
0,0616 |
0,9179 |
0,0019 |
0,0285 |
0,0010 |
|
3800 |
95,4896 |
362860,5 |
0,037 |
0,0821 |
1,0000 |
0,0030 |
0,0370 |
0,0014 |
|
Сумма |
2580,8 |
4417297 |
1,000 |
1,0000 |
|
0,1381 |
0,4359 |
0,1721 |
Коэффициент
К.Джини равен ![]() (26,6%).
(26,6%).
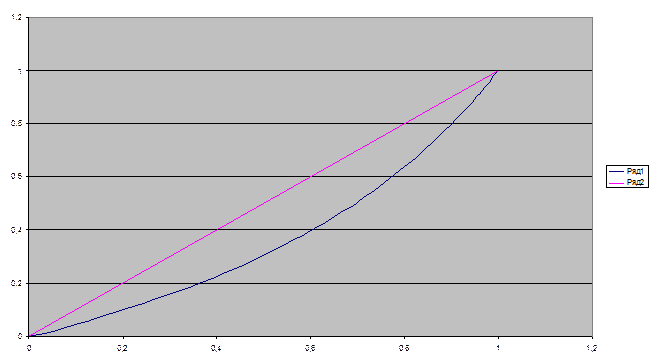
Кривая Лоренца:
Составляем вспомогательную таблицу по численности населения:
|
|
|
|
|
|
|
|
|
|
|
600 |
193,56 |
116136 |
0,0750 |
0,0246 |
0,0246 |
0,0018 |
0,0018 |
0,0056 |
|
1000 |
603,9072 |
603907,2 |
0,2340 |
0,1280 |
0,1526 |
0,0299 |
0,0357 |
0,0548 |
|
1400 |
560,0336 |
784047 |
0,2170 |
0,1662 |
0,3187 |
0,0361 |
0,0692 |
0,0471 |
|
1800 |
348,408 |
627134,4 |
0,1350 |
0,1329 |
0,4517 |
0,0179 |
0,0610 |
0,0182 |
|
2200 |
216,7872 |
476931,8 |
0,0840 |
0,1011 |
0,5527 |
0,0085 |
0,0464 |
0,0071 |
|
2600 |
188,3984 |
489835,8 |
0,0730 |
0,1038 |
0,6565 |
0,0076 |
0,0479 |
0,0053 |
|
3000 |
172,9136 |
518740,8 |
0,0670 |
0,1099 |
0,7665 |
0,0074 |
0,0514 |
0,0045 |
|
3400 |
64,52 |
219368 |
0,0250 |
0,0465 |
0,8130 |
0,0012 |
0,0203 |
0,0006 |
|
3800 |
232,272 |
882633,6 |
0,0900 |
0,1870 |
1,0000 |
0,0168 |
0,0900 |
0,0081 |
|
сумма |
2580,8 |
4718735 |
1,0000 |
1,0000 |
|
0,1272 |
0,4237 |
0,1513 |
Коэффициент
К.Джини равен ![]() (28%).
(28%).
Кривая Лоренца:

в)
Коэффициент Херфиндаля-Хиршмана определяется как сумма квадратов долей всех групп ![]() .
.
Коэффициент
Херфиндаля-Хиршмана по числу
домохозяйств ![]() .
.
Коэффициент
Херфиндаля-Хиршмана по численности населения
![]() .
.
4. Численность населения региона, имеющего доход ниже прожиточного минимума, установленного в размере 1530 руб по числу домохозяйств равна 1481,4 тыс. чел.
Численность населения региона, имеющего доход ниже прожиточного минимума, установленного в размере 1530 руб по численности населения равна 1357,5 тыс. чел.
5. Уровень бедности в регионе по числу домохозяйств: 1481,4/2580,8 = 0,574(57,4%).
Уровень бедности в регионе по численности населения: 1357,5/2580,8 = 0,526(52,6%).
Вывод: По числу домохозяйств среднедушевой месячный доход населения региона равен1711,6.; уровень концентрации доходов равен 26,6%; уровень бедности равен 57,4%.
По численности населения среднедушевой месячный доход населения региона равен 1828,4;
уровень концентрации доходов равен 28%; уровень бедности равен 52,6%.