Содержание

Задание 1. 3

Задание 2. 6

Вопрос 5. Элементы теории игр. 7

1. Основные понятия теории игр. 7

2. Классификация игр. 9

3. Формальное представление игр. 10

4. Принципы решения матричных антагонистических игр. 13

Глоссарий экономических терминов.. 17

Список литературы... 21

Задание 1.

Построить график (вершинный и сетевой) на основе следующей информации

А	Б	В	Г	Д	Е	Ж	З	И	К	Л	М
–	–	–	В	В	А	В	Д Ж	А	Е	Д Ж	Б Г З
Н	О	П	Р	С	Т	У	Ф	Х	Ц	Ч	Ш
Б Г З	М	И	И	К Л М	К П	Р С	Л М Н	О	Т У Ф Х	Ц	Ч

Решение:

Ниже на рисунке 1 изображается сетевой график, на котором помещены события, наступающие после окончания соответствующих работ, и связывающие эти события работы. При построении этого графика не было необходимости вводить фиктивные события и фиктивные работы – каждая работа связана с теми работами, которые, согласно таблице, ей предшествуют. Например, рассмотрим событие №8; согласно таблице, работа «М» опирается на работы «Б», «Г» и «З», значит, по правилам построения сетевого графика работы «Б», «Г» и «З» предшествуют событию №8, а работа «М» начинается после наступления события №8. Аналогично работа «Н».

На рисунке 2 изображен вершинный график, показывающий связи между работами.

 

Рисунок 1. Сетевой график

 

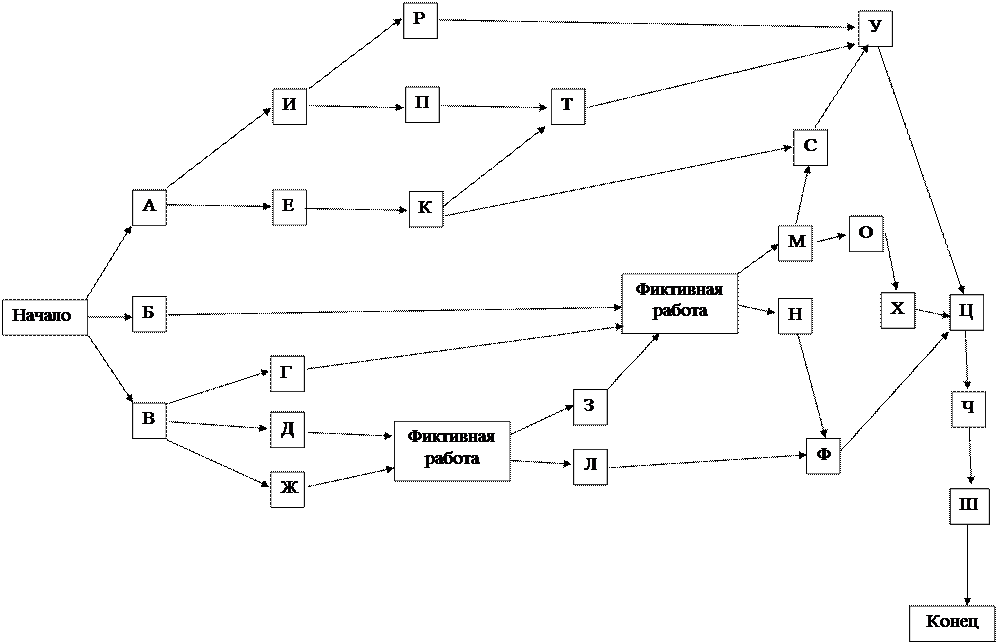
Рисунок 2. Вершинный график    

Задание 2

Пронумеровать события, используя сетевые графики задания 2, рассчитать временные параметры всех работ и событий.

Исходные данные

работы	Тосл	Тнорм	Тфорс
1	2	3	4	5	1	2	3	4	5	1	2	3	4	5
К	16	12	16	16	10	11	10	14	15	9	10	8	12	11	8

Решение:

По формуле 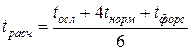 найдем расчетное время продолжительности работ. Так, для работы №1 продолжительность:

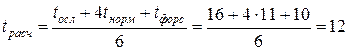 дней.

При расчете произведено округление в сторону большего целого числа.

Аналогично для других работ:

№2: 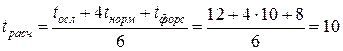 дней.

№3: 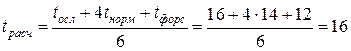 дней.

№4: 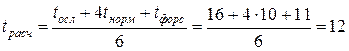 дней.

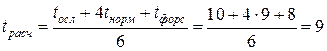№5:  дней.

Таким образом, продолжительность всех работ:

работы	Продолжительность, в днях
1	2	3	4	5
К	12	10	16	12	9

Вопрос 5. Элементы теории игр

1. Основные понятия теории игр

Теория игр рассматривает задачи принятия решений в ситуациях с несколькими участниками, когда значение целевой функции для каждого из субъектов зависит и от решений, принимаемых всеми остальными участниками. Предметом теории игр являются такие ситуации, в которых важную роль играют конфликты и совместные действия.

Одна из характерных черт всякого общественного, социально-экономического явления состоит в множественности, многосторонности интересов и в наличии сторон, выражающих эти интересы. Классическими примерами здесь являются ситуации, где, с одной стороны, имеется один покупатель, с другой – продавец (ситуация монополия – монопсония), когда на рынок выходят несколько производителей, обладающих достаточной силой для воздействия на цену товара (ситуация олигополии, в том числе дуополии, если число таких участников равно двум). Более сложные ситуации подобного рода возникают, если имеются объединения или коалиции лиц, участвующих в столкновении интересов, например, в том случае, когда ставки заработной платы определяются союзами или объединениями рабочих и предпринимателей, при анализе результатов голосования в парламенте и т.п.

Конфликт может возникнуть также из различия целей, которые отражают не только несовпадающие интересы различных сторон, но и многосторонние интересы одного и того же лица. Например, разработчик экономической политики обычно преследует разнообразные цели, согласуя противоречивые требования, предъявляемые к ситуации (рост объемов производства, повышение доходов, снижение экологической нагрузки и т.п.). Конфликт может проявляться не только в результате сознательных действий различных участников, но и как результат действия тех или иных "стихийных сил" (случай так называемых "игр с природой"). Множество подобных примеров можно встретить в биологии, социологии, психологии, политологии, военном деле и т.д.

И наконец, примерами игр являются обычные игры: салонные спортивные, карточные и др. Именно с анализа подобных игр начиналась математическая теория игр; они и по сей день служат прекрасным материалом для иллюстрации положений и выводов этой теории.

В итоге, всякая претендующая на адекватность математическая модель социально-экономического явления должна отражать присущие ему черты конфликта, т.е. описывать:

а) множество заинтересованных сторон (мы будем называть их игроками; в литературе по теории игр они именуются также субъектами, лицами, сторонами, участниками). В случае, если число игроков конечно, они различаются по своим номерам (1-й игрок и 2-й игрок в игре в орлянку или в случае дуополии) или по присваиваемым им именам (например, продавец и покупатель в ситуации монополия – монопсония);

б) возможные действия каждой из сторон, именуемые также стратегиями или ходами;

в) интересы сторон, представленные функциями выигрыша (платежа) для каждого из игроков.

В теории игр предполагается, что функции выигрыша и множество стратегий, доступных каждому из игроков, общеизвестны, т.е. каждый игрок знает свою функцию выигрыша и набор имеющихся в его распоряжении стратегий, а также функции выигрыша и стратегии всех остальных игроков, и в соответствии с этой информацией организует свое поведение.

Формализация содержательного описания конфликта представляет собой его математическую модель, которую называют игрой.

Теория игр впервые была систематически изложена Дж. фон Нейманом и О. Монгерштерном в 1944 г., хотя отдельные результаты были опубликованы еще в 20-х годах. Нейман и Моргенштерн на­писали оригинальную книгу, которая содержала главным образом экономические примеры, поскольку экономическому конфликту легче всего придать численную форму. Во время второй мировой войны и сразу после нее теорией игр серьезно заинтересовались военные, которые увидели в ней аппарат для исследования стратегических решений. Затем главное внимание снова стало уделяться экономическим проблемам. Сейчас ведется большая работа, направленная на расширение сферы применения теории игр.

2. Классификация игр

Различные виды игр можно классифицировать, основываясь на том или ином принципе: по числу игроков, по числу стратегий, по свойствам функций выигрыша, по возможности предварительных переговоров и взаимодействия между игроками в ходе игры.

В зависимости от числа игроков различают игры с двумя, тремя и более участниками. Весь материал, представленный в теории оптимизации, можно рассматривать как теорию игр с одним игроком. В принципе возможны также игры с бесконечным числом игроков.

Согласно другому принципу классификации—по количеству стратегий—различают конечные и бесконечные игры. В конечных играх игроки располагают конечным числом возможных стратегий (например, в игре в орлянку игроки имеют по два возможных хода—они могут выбрать "орел" или "решку"). Сами стратегии в конечных играх нередко называются чистыми стратегиями (смысл этого названия будет ясен далее). Соответственно, в бесконечных играх игроки имеют бесконечное число возможных стратегий—так в ситуации Продавец-Покупатель каждый из игроков может назвать любую устраивающую его цену и количество продаваемого (покупаемого) товара.

Третий способ классификации игр—по свойствам функции выигрыша (платежных функций). Важным случаем в теории игр является ситуация, когда выигрыш одного из игроков равен проигрышу другого, т.е. налицо прямой конфликт между игроками. Подобные игры называются играми с нулевой суммой, или антагонистическими играми. Игры в орлянку или в очко—типичные примеры антагонистических игр. Прямой противоположностью играм такого типа являются игры с постоянной разностью, в которых игроки и выигрывают, и проигрывают одновременно, так что им выгодно действовать сообща. Между этими крайними случаями имеется множество игр с ненулевой суммой, где имеются и конфликты, и согласованные действия игроков.

В зависимости от возможности предварительных переговоров между игроками различают кооперативные и некооперативные игры. Игра называется кооперативной, если до начала игры игроки образуют коалиции и принимают взаимообязывающие соглашения о своих стратегиях. Игра, в которой игроки не могут координировать свои стратегии подобным образом, называется некооперативной. Очевидно, что все антагонистические игры могут служить примером некооперативных игр. Примером кооперативной игры может служить ситуация образования коалиций в парламенте для принятия путем голосования решения, так или иначе затрагивающего интересы участников голосования.

3. Формальное представление игр

Дадим формальное описание перечисленных элементов конфликта. Множество всех игроков, обозначаемое I, в случае конечного их числа может задаваться простым перечислением игроков. Например, I={1, 2} при игре в орлянку, I={Продавец, Покупатель} в ситуации монополия—монопсония, I={1, 2, ..., n} в случае анализа результатов голосования в парламенте.

Множество стратегий игрока i обозначим через Х_i. При игре в орлянку каждый игрок располагает двумя стратегиями: Х_i={0рел, Решка}; каждый участник голосования имеет выбор на множестве стратегий {За, Против}. В случае взаимодействия на рынке как Продавец, так и Покупатель могут назначать некоторую неотрицательную цену на продаваемый (покупаемый) товар, т.е. множество стратегий каждого из них X_i: Р_i> 0.

В каждой партии игрок выбирает некоторую свою стратегию х_i X_i, в результате чего складывается набор стратегий х_i={x₁, x₂,..., x_n}, называемый ситуацией. Так, ситуацию в Парламенте описывает список {За, За, Против, За...}, полученный в итоге проведенного голосования.

Заинтересованность игроков в ситуациях проявляется в том, что каждому игроку I в каждой ситуации х приписывается число, выражающее степень удовлетворения его интересов в данной ситуации. Это число называется выигрышем игрока и обозначается через h_i(х), а соответствие между набором ситуаций и выигрышем игрока I называется функцией выигрыша (платежной функцией} этого игрока Н_i.

В случае конечной игры двух лиц функции выигрыша каждого из игроков удобно представлять в виде матрицы выигрышей, где строки представляют стратегии одного игрока, столбцы - стратегии другого игрока, а в клетках матрицы указываются выигрыши каждого из игроков в каждой из образующихся ситуаций. (Данная форма представления конечных игр двух лиц объясняет общее для них название—матричные игры.)

Например, в случае игры в орлянку каждый из игроков имеет по две стратегии, именуемые Орел и Решка. Если игроки выбирают одинаковые стратегии, т.е. в случаях, если оба говорят "Орел" или оба говорят "Решка", 1-й игрок выигрывает 1 рубль, а второй игрок проигрывает 1 рубль. В ситуациях, когда оба игрока выбирают различные стратегии, 1-й игрок проигрывает 1 рубль, а 2-й игрок соответственно этот 1 рубль выигрывает.

В итоге матрица выигрышей 1-го игрока H₁, выглядит следующим образом:

Стратегии 1-го игрока	Стратегии 2-го игрока
	Орел	Решка
Орел	1	-1
Решка	-1	1

Соответственно будет выглядит и матрица выигрышей 2-го игрока:

Стратегии 1-го игрока	Стратегии 2-го игрока
	Орел	Решка
Орел	-1	1
Решка	1	-1

Для антагонистических игр, в которых выигрыш одного игрока равен проигрышу другого (игр с нулевой суммой), выполняется соотношение Н₁=- Н₂. Игра в орлянку, очевидно, является примером такой игры.

Часто для наглядности матрицы выигрышей для обоих игроков совмещают в одну, которая дает полное представление о всей игре:

Стратегии 1-го игрока	Стратегии 2-го игрока
	Орел	Решка
Орел	(1, -1)	(-1, 1)
Решка	(-1, 1)	(1, -1)

В каждой клетке этой матрицы слева указаны значения выигрыша 1-го игрока, справа—значения выигрыша 2-го игрока.

Рассмотрим пример задания матрицы выигрышей для игры с ненулевой суммой, называемой в литературе по теории игр Дилемма Заключенного. Содержание игры следующее: два преступника ожидают приговора суда за совершенное злодеяние. Адвокат конфиденциально предлагает каждому из преступников облегчить его участь (и даже освободить!), если он сознается и даст показания против сообщника, которому грозит угодить в тюрьму за совершенное преступление на 10 лет. Если никто не сознается, то обоим угрожает заключение на определенный срок (скажем, 1 год) по обвинению в незначительном преступлении. Если сознаются оба преступника, то, с учетом чистосердечного признания, им обоим грозит попасть в тюрьму на 5 лет. Каждый заключенный имеет на выбор 2 стратегии: не сознаваться или сознаваться, выдав при этом сообщника. В итоге можно получить следующую матрицу "выигрышей" для обоих игроков.

Стратегии 1-го игрока	Стратегии 2-го игрока
	Сознаться	Не сознаться
Сознаться	5; 5	0; 10
Не сознаться	10; 0	1; 1

Приведем, наконец, пример записи функции выигрыша для бесконечной игры. В случае дуополии каждый из игроков может объявить цену р_j, по которой он хотел бы продать некоторое количество товара. При этом предполагается, что потребители приобретут товар у фирмы, объявившей меньшую цену, или распределят свой спрос поровну между фирмами в случае, если они назначили одинаковую цену. Если функцию спроса в зависимости от цены на товар обозначить как d(р), то функция выигрыша 1-й фирмы П₁(p₁, p₂) будет иметь вид:

П1(p1, p2)={

p1d(p1), если p1<p2 p1*d(p1)/2, если p1=p2 0, если p1>p2

Аналогично выглядит функция выигрыша 2-й фирмы П₂(р₁, р₂).

4. Принципы решения матричных антагонистических игр

В качестве основного допущения в теории игр предполагается, что каждый игрок стремится обеспечить себе максимально возможный выигрыш при любых действиях партнера. Предположим, что имеется конечная антагонистическая игра с матрицей выигрышей 1-го игрока H и, соответственно, матрицей выигрыша 2-го игрока -Н. Пусть Игрок 1 считает, что какую бы стратегию он ни выбрал, Игрок 2 выберет стратегию, максимизирующую его выигрыш, и тем самым минимизирующую выигрыш Игрока 1. Оптимальная стратегия Игрока 1, которая обеспечит ему наибольший из возможных выигрышей вне зависимости от стратегии противника, будет состоять в выборе стратегии с самым высоким из таких платежей. Таким образом, Игрок 1 выбирает 1-ю стратегию, которая является решением задачи

max min h_ij

^{i j}

Игрок 2 точно так же стремится обеспечить себе наивысшую величину выигрыша (или, что эквивалентно, наименьшую величину проигрыша) вне зависимости от стратегии, избранной партнером. Его оптимальной стратегией будет столбец матрицы Н с наименьшим значением максимального платежа. Таким образом, Игрок 2 выберет j-ю стратегию, которая является решением задачи

min max h_ij

^{j i}

В итоге, если Игрок 1 придерживается избранной стратегии (называемой максиминной стратегией), его выигрыш в любом случае будет не меньше максиминного значения (называемого также нижней ценой игры), т.е.

h_ij ≥ max min h_ij

^{i j}

Соответственно, если Игрок 2 придерживается своей минимакс­ной стратегии, его проигрыш будет не больше минимаксного значения (называемого верхней ценой игры}, т.е.

h_ij ≤ min max h_ij

^{j i}

В случае, если верхняя цена игры равна нижней, т.е.

max min h_ij = min max h_ij = h_ij*

^{i j j i}

оба игрока получают свои гарантированные платежи, а значение h_ij* называется ценой игры. Элемент h_ij матрицы выигрышей, соответствующий максиминной и минимаксной стратегиям, называется седловой точкой матрицы H (это объясняется формой графика функции выигрыша в точке h_ij: она напоминает седло, убывая при изменении одной из переменных и возрастая при изменении другой переменной). В случае, если цена антагонистической игры равна О, игра называется справедливой.

Рассмотрим игру, в которой Игрок 1 располагает двумя стратегиями, а Игрок 2 - тремя. Пусть матрица выигрышей Игрока 1 имеет следующий вид:

H1=	2	1	4
-1	0	6

(Поскольку мы рассматриваем пример антагонистической игры, матрица выигрышей Игрока 2 будет равна H₁, взятой с обратным знаком, т.е. H₂ =-H₁.)

Игрок 1 рассчитывает, что если он выберет первую стратегию (т.е. первую строку матрицы H₁), то противник может выбрать свою вторую стратегию (второй столбец), так что выигрыш будет равен 1. Если же он выберет вторую стратегию, то противник может избрать первую стратегию, так что выигрыш будет равен -1. Проанализировав полученные значения, Игрок 1 останавливается на своей первой стратегии, которая обеспечивает ему максимальный гарантированный выигрыш, равный 1.

Точно так же Игрок 2 рассматривает свои наихудшие варианты, когда противник выбирает свою первую стратегию, если Игрок 2 выбирает первую или вторую стратегии, или когда противник выбирает вторую стратегию, когда Игроком 2 выбран третий столбец. Эти варианты соответствуют максимальным значениям столбцов 2, 1 и 6. Взяв минимальное значение этих максимумов, Игрок 2 останавливается на своей второй стратегии, при которой его проигрыш минимален и равен 1:

min h_ij

^j

max hij i	2	1	4		1	max min hij i j
-1	0	6		-1
2	1	6
min max hij i j

 

Следовательно, в этой игре существуют совместимые выборы, т.е.

h* = max min h_ij = min max h_ij =1

                ^{i j j i}

В итоге будет разумно ожидать, что в описанной выше игре противники будут придерживаться избранных стратегий. Матричная антагонистическая игра, для которой

max min h_ij = min max h_ij

^{i j j i}

называется вполне определенной, или игрой, имеющей решение в чистых стратегиях.

Глоссарий экономических терминов

1.       Баланс - система показателей, характеризующая какое-либо явление путем сопоставления или противопоставления отдельных его сторон. В экономической науке различают бухгалтерские балансы, консолидированные балансы, платежные балансы и торговые балансы.

2.        Валовой внутренний продукт - совокупная стоимость всех товаров и услуг, произведенных в течение года на территории страны без разделения ресурсов, использованных на их производство, на импортные и внутренние. Для большинства стран мира показатели ВВП и ВНП различаются незначительно и зачастую считаются взаимозаменяемыми. Чаще всего используют два метода расчета ВВП:         -1- путем суммирования всех доходов в экономике: заработной платы, процентов на капитал, прибыли и ренты;          -2- путем суммирования всех произведенных расходов: потребления, инвестиций, государственных закупок товаров и услуг, а также чистого экспорта. Теоретически результаты вычислений в обоих случаях должны совпадать, поскольку расходы одного участника экономических отношений всегда являются доходами для другого.

3.        Измерение национального дохода и продукта - определение произведенного нацией в течение фиксированного отрезка времени объема товаров и услуг, а также доходов, которые нация получила от их производства.

4.       Исследование операций - математическая дисциплина, занимающаяся разработкой и применением методов нахождения наилучших решений в различных областях человеческой деятельности. Исследование операций исходит из того, что в модели реальной проблемы имеются: - цель, которая должна быть достигнута; - ограничения, которые должны быть удовлетворены;        - параметры, управляя которыми, можно достичь цель.

5.       Макроэкономика - один из двух основных разделов экономической науки, изучающий: - поведение экономики как единого целого, состоящего из экономических агентов; - закономерности взаимодействия (а) совокупных величин общего уровня цен и безработицы, (б) общего потребления и инвестиций, (в) общего спроса и общего предложения, а также их влияние на (г) изменения объема производства и на (д) экономический рост. Макроэкономика оперирует агрегированными макроэкономическими показателями.

6.        Математическая модель - модель объекта, процесса или явления, представляющая собой математические закономерности, с помощью которых описаны основные характеристики моделируемого объекта, процесса или явления. Математическое программирование - раздел математики, исследующий математические модели и методы решения многоэкстремальных задач с ограничениями. Задачи математического программирования подразделяются на: - выпуклые: линейное и выпуклое программирование; - динамические: динамическое программирование; - сетевые; - дискретные: решение в целых числах; и - стохастические: стохастическое программирование.

7.       Модель - создаваемое человеком подобие изучаемых объектов: макеты, изображения, схемы, словесные описания, математические формулы, карты и т.д. Модели всегда проще реальных объектов, но они позволяют выделить главное, не отвлекаясь на детали. Различают математические, физические, ситуационные и электрические модели.

8.       Модель "доходы-расходы" – кейнсианская модель равновесия национального дохода, в которой:          - планируемые расходы (совокупный спрос) и национальный продукт (совокупное предложение) являются функцией дохода и не зависят от цен, которые остаются фиксированными;  а - национальный продукт равен национальному доходу, который, в свою очередь, равен располагаемому доходу вместе с чистыми налогами.

9.        Национальный продукт - общая стоимость всех товаров и услуг, произведенных экономикой. Национальный продукт представляет собой поток денежных расходов домохозяйств, который движется навстречу потоку товаров и услуг. При равновесии кругооборота доходов и продукции национальный продукт равен национальному доходу.

10.    Планирование - вид управленческой деятельности, связанный: - с определением целей управляемой системы;   - c поиском наиболее эффективных методов и средств, необходимых для достижения этих целей;  и - c формулированием системы показателей, определяющих ход работ по достижению поставленных целей. Результатом планирования является план.

11.   Поток денежных средств - разность между суммами поступлений и выплат денежных средств компании за определенный период времени (обычно - за финансовый год). Предельная склонность к потреблению - доля расходов на потребительские товары в любом изменении располагаемого дохода.

12.    Предельная склонность к потреблению равна изменению в потреблении, деленному на изменение располагаемого дохода. Между предельной склонностью к сбережению (MPS) и предельной склонностью к потреблению существует обратная зависимость: MPS = 1 - MPC.

13.    Предельная склонность к сбережению - доля сбережений в любом изменении личного располагаемого дохода. Предельная склонность к сбережению равна изменению объема сбережений, деленному на изменение дохода после уплаты налогов.

14.    Прогноз - оценка будущей тенденции, с помощью исследования и анализа доступной информации. Прогноз - вероятностное суждение о некоторого явления.

15.    Простой мультипликатор - мультипликатор расходов в упрощенной экономической модели, характеризующейся отсутствием чистых налоговых поступлений у правительства, отсутствием импорта, а также тем, что инвестиции не зависят от уровня дохода. Простой мультипликатор равен единице, деленной на предельную склонность к сбережениям.

16.   Сложный мультипликатор - мультипликатор расходов, используемый в такой экономической модели, когда изменение ВВП вызывается не только изменением объема сбережений, но и изменением чистых налоговых поступлений и объема импорта. Мультипликатор расходов есть величина обратная 1 - (MPS - MPM) * (1 - t), где MPS - предельная склонность к сбережениям; MPM - предельная склонность к импорту; t - предельная ставка налога.

17.    Совокупный денежный поток - сумма денежных потоков от операционной, инвестиционной и финансовой деятельности предприятия.

18.    Экономика - развивающаяся в рамках общественно-исторической формации на базе сложившихся производительных сил и производственных отношений стратегия и тактика хозяйственной деятельности, охватывающие все звенья товарного производства, распределения, товародвижения и потребления материальных благ.

19.    Экономико-математическая модель - математическая модель связи экономических характеристик и параметров системы. Экономико-математическая модель описывает экономические процессы, объекты и связи с использованием математического аппарата.

20.    Экономический прогноз - результат научных исследований о возможных направлениях будущего развития экономики и ее отдельных сегментов.

Список литературы

1.                Абрютина М.С. Грачев А.В. Экономико-математические методы. Учебно-практическое пособие. – М.: «Дело и сервис», 1998.

2.                Базаров К.Л., Баканов М.И. Теория игр. - Н.: Учебник  Финансы и статистика, 1997.

3.                Завьялова З. М. Теория игр и ее применения. – М.: Инфра-М, 2002

4.                Грищенко О.В. Математические методы в экономике. Теория игр. Учебное пособие. – Таганрог: Изд-во ТРТУ, 2000.

5.                Савицкий А.В. Экономико-математические методы и модели. – Мн.: ИП «Экоперспектива», 1998.