Содержание
1.
Теоретическая часть. 3
1.2. Понятие динамического ряда. 3
1.2. Разложение динамических рядов на компоненты.. 3
1.3. Аддитивная форма представления динамических рядов. 4
1.3.
Полумультипликативные модели. 5
1.4. Использование
сочетаний аддитивных и полумультипликативных моделей на практике. 6
2. Практическая часть. 15
Список литературы.. 18
1. Теоретическая часть
1.2. Понятие динамического ряда
Динамическим рядом называют серию числовых величин, полученных через
регулярные промежутки времени. Например динамическими рядами будут серия ежедневных наблюдений в
течение некоторого периода за ценами товара при закрытии торгов на бирже,
дневные объемы выпуска товара, месячные показатели инфляции или индекса
потребительских цен, ежеквартальные оценки валового национального продукта
(принятые в США) или средних зарплат (принятые в России для ежеквартального
индексирования пенсий), ежегодные данные об объеме, выручке и прибыли компании.
Динамические ряды, естественно, не ограничиваются исключительно экономическими
величинами; известно их использование при анализе процессов в энергосистемах,
атомной промышленности, химических и нефтехимических производствах, причем в
этом случае часто используются более мелкие дискретности времени, чем в
экономике - минуты и даже секунды при обработке данных о быстропротекающих
процессах в атомной энергетике или при исследовании переходных процессов в
химической кинетике. Известно даже успешное применение анализа динамических рядов при слежении за подводными лодками
"вероятного противника" в 70-80-е годы, и при обработке данных
наблюдений в системах ПВО, и при прогнозах проходимости радиосигналов в
атмосфере и ионосфере, и при моделировании транспортных потоков на автотрассах.
1.2. Разложение динамических рядов на компоненты
В спектральном анализе исследуются периодические модели данных. Цель анализа
- разложить комплексные динамические ряды с циклическими компонентами на несколько
основных синусоидальных функций с определенной длиной волн. Термин "спектральный"
- своеобразная метафора для описания природы этого анализа. Предположим, вы
изучаете луч белого солнечного света, который, на первый взгляд, кажется
хаотически составленным из света с различными длинами волн. Однако, пропуская
его через призму, вы можете отделить волны разной длины или периодов, которые
составляют белый свет. Фактически, применяя этот метод, вы можете теперь
распознавать и различать разные источники света. Таким образом, распознавая
существенные основные периодические компоненты, вы узнали что-то об
интересующем вас явлении. В сущности, применение спектрального анализа к
временным рядам подобно пропусканию света через призму. В результате успешного
анализа можно обнаружить всего несколько повторяющихся циклов различной длины в
интересующих вас динамических рядах, которые, на первый взгляд, выглядят как случайный
шум[2, с. 135].
Наиболее известный пример применения спектрального анализа - циклическая
природа солнечных. Оказывается, что активность солнечных пятен имеет 11-ти
летний цикл. Другие примеры небесных явлений, изменения погоды, колебания в
товарных ценах, экономическая активность и т.д. также часто используются в
литературе для демонстрации этого метода. В отличие от метода экспоненциального
сглаживания, цель спектрального анализа - распознать сезонные колебания
различной длины, в то время как в предшествующих типах анализа, длина сезонных
компонент обычно известна (или предполагается) заранее и затем включается в
некоторые теоретические модели скользящего среднего или автокорреляции.
1.3. Аддитивная форма представления динамических рядов
Существуют две основные цели анализа динамических рядов[9, с. 58]:
(1) определение природы ряда
(2) прогнозирование (предсказание будущих значений динамического ряда по настоящим и прошлым значениям). Обе
эти цели требуют, чтобы модель ряда была идентифицирована и, более или менее,
формально описана. Как только модель определена, вы можете с ее помощью
интерпретировать рассматриваемые данные (например, использовать в вашей теории
для понимания сезонного изменения цен на товары, если занимаетесь экономикой).
Не обращая внимания на глубину понимания и справедливость теории, вы можете экстраполировать
затем ряд на основе найденной модели, т.е. предсказать его будущие значения.
Аддитивные модели представляют собой обобщение Множественной регрессии
(которая является частным случаем общей линейной
модели). В частности, в линейной регрессии линейная подгонка
методом наименьших квадратов вычисляется для набора предикторов или переменных
Х, чтобы предсказать зависимость переменной У. Хорошо известное уравнение
линейной регрессии с m предикторами можно сформулировать, как:
Y = b0 + b1*X1 + .. bm*Xm, (1)
Где Y обозначает зависимую переменную (для предсказанных значений),X1 при
помощи Xm представляет m значения для предсказанных переменных, а b0, и b1 при
помощи bm коэффициенты регрессии, оцененные при помощи множественной
регрессии. Обобщение множественной регрессионной модели
сохраняет аддитивную природу модели, но перемещая простые члены линейного
уравнения bi*Xi с fi(Xi), где fi непараметрическая функция предиктора Xi.
Другими словами, вместо отдельного коэффициента для каждой переменной
(аддитивного элемента) в модели в аддитивных моделях не уточненная (непараметрическая)
функция оценивается для каждого предиктора, чтобы получить наилучшее
предсказание значения зависимой переменной.
На практике наибольшее распространение получили аддитивные модели, в
которых влияния различных объясняющих факторов складываются.
y = β0 + β1x1 + β2x2 + … + βmxm + u, (2)
1.3. Полумультипликативные модели
Основным положением, на котором базируется использование динамических рядов для прогнозирования, является то, что
факторы, влияющие на отклик изучаемой системы, действовали некоторым образом в
прошлом и настоящем, и ожидается, что они будут действовать схожим образом и в
не слишком далеком будущем. Поэтому основной целью анализа временных рядов будет
оценка и вычленение этих влияющих факторов с целью прогноза дальнейшего
поведения системы и выработки рациональных управленческих решений.
В свое время были разработаны многие методы вычленения влияющих факторов
и оценки их взаимодействия и влияния на отклик системы, но пожалуй наиболее
фундаментальной является классическая полумультипликативная модель динамического
ряда, широко используемая при анализе ежемесячных, ежеквартальных и ежегодных
данных, и потому чаще всего используемая в экономических исследованиях[6, с.138].
В практике оценки наряду с аддитивными моделями широко используются полумультипликативные модели.
y = β0 · x1β1 · K · xjβj · βj+1xj+1
· K · βKxK · u, (3)
В полумультипликативной модели
переменные не умножаются на свои коэффициенты. Вместо этого они либо возводятся
в степени, либо сами служат в качестве показателя степени, а результаты затем
перемножаются. Случайная составляющая u также входит в модель полумультипликативно.
Для оценки параметров полумультипликативной модели её сначала необходимо
преобразовать к аддитивному виду путём логарифмирования, а затем применить
метод наименьших квадратов. Модель после
логарифмирования имеет вид:
ln y = ln β0 + β1ln x1 + K +
βjln xj + xj+1ln βj+1 + K + xKln βK + ln u, (4)
1.4. Использование сочетаний аддитивных
и полумультипликативных моделей на
практике
Более сложный вид имеют гибридные модели, которые сочетают в себе
аддитивные и полумультипликативные
компоненты. Гибридная модель даёт оценщику большую свободу, что позволяет ему
строить более качественные и содержательные модели.
y = (β0 + β1x1 + β2x2 + … +
βjxj)α1 · xj+1α2 · K · xKβkj · βk+1xk+1 · K ·
βmxm · u, (5)
Однако в гибридных моделях нельзя получать оценки параметров непосредственно
с помощью метода наименьших квадратов. Для каждой модели приходится искать
подходящий способ оценки параметров, один из таких способов будет рассмотрен
далее на примере построения модели стоимости доходной недвижимости.
Если же невозможно сразу сделать уверенный выбор какой-либо одной
функции, то отбирают несколько функции, рассчитывают их параметры и далее,
используя соответствующие критерии качества модели, окончательно выбирают
функциональный вид исследуемой зависимости[8, с. 11].
Для построения
регрессионной модели стоимости (в US$) 1 м2 общей внутренней площади
(этот показатель был выбран как результирующих фактор) были определены и
рассчитаны следующие качественные и количественные факторные переменные:
- Качественные переменные
- Функциональное назначение отражают четыре бинарные
переменные. С их помощью описывается принадлежность объекта к:
- офисному помещению;
- торговому помещению (магазины, аптеки);
- помещению, предназначенному для размещения
предприятия общественного питания (кафе, столовые, рестораны);
- помещению, предназначенному для размещения
предприятия службы быта (мастерские, ателье, парикмахерские).
- Местоположение объекта описано с помощью четырёх
бинарных переменных:
- центральная зона города — зона 4;
- зона города, приближённая к центральной (центры
деловой активности и места транспортных развязок) — зона 3;
- серединная зона города — зона 2;
- окраина города — зона 1.
- Количественные
переменные
- Доля подвала, определяемая как отношение площади
подвала к общей площади. Это безразмерная переменная; она принимает
значение от 0 (если подвала нет) до 1 (если помещение полностью
расположено в подвале).
- Возраст на момент оценки определяется как разность лет
от года оценки объекта до года постройки здания.
- Общая внутренняя площадь объекта в м2.
- Коэффициент, характеризующий отношение общей наружной и
внутренней площадей (отражает толщину стен и положение в здании).
- Средняя высота помещения, измеряется в метрах,
определяется как частное от деления строительного объёма на площадь
объекта.
- Средневзвешенный физический износ объекта, в долях
единицы.
- Курс рубля к US$ по данным НБУ на дату оценки.
- Стоимость улучшения 1 м2, измеряются в US$
по курсу НБУ на дату оценки.
- Инженерное обеспечение. Для всех объектов известно
наличие или отсутствие каждой из 10 характеристик: электроснабжение,
теплоснабжение, водоснабжение, канализация, вентиляция/кондиционирование,
лифт, телефон, радио, телевидение, сигнализация. Некоторые из них были исключены
из базы, как не влияющие на рассматриваемые объекты (лифт, радиоточка),
или характерные для всех объектов (электроснабжение). Использование для
описания оставшихся 7 бинарных переменных привело бы к чрезмерной
перегруженности модели. По этой причине, для обобщённой характеристики
наличия инженерного обеспечения используется коэффициент, рассчитанный как
сумма семи взвешенных бинарных переменных. Вес каждой переменной был
рассчитан с помощью симплекс-метода, средствами модуля «Поиск решения»
пакета электронных таблиц Microsoft Excel™, исходя из предположения, что
наличие определённой характеристики положительно влияет на его рыночную
стоимость; при этом наличие всех характеристик обращает коэффициент в 1, а
отсутствие — в 0. Таким образом, имеем коэффициент инженерного
обеспечения — безразмерную количественную переменную, принимающую
значение от 0 до 1.
В ходе анализа
взаимосвязи перечисленных выше факторов с результирующим показателем отдельно
анализировались качественные и количественные переменные.
Для качественных
признаков были построены таблицы сопряжённости, с помощью которых определялась
их взаимосвязь со значением результирующей переменной. Для этого весь интервал
значений стоимости 1 м2 внутренней площади был разбит на 4 равных
интервала:
- от 28 US$ до 68 US$,
- от 68 US$ до 108 US$,
- от 108 US$ до 148 US$,
- от 148 US$ до 188 US$.
После этого рассчитывалось, сколько
значений каждой бинарной переменной попадает в каждый из интервалов стоимости.
В таблицах 1 и 2 приводятся данные о распределении
выборочных данных в зависимости от значений качественных факторов
(местоположения и функционального назначения).
|
Таблица
1
Таблица
сопряжённости факторов стоимости и местоположения
|
|
Стоимость
1 м2, US$
|
Местоположение
|
Сумма
|
|
Зона 4
|
Зона 3
|
Зона 2
|
Зона 1
|
|
[28; 68)
|
3
|
3
|
3
|
2
|
11
|
|
[68; 108)
|
18
|
15
|
11
|
2
|
46
|
|
[108; 148)
|
17
|
7
|
1
|
0
|
25
|
|
[148; 188]
|
6
|
2
|
0
|
0
|
8
|
|
Сумма
|
44
|
27
|
15
|
4
|
90
|
Таблица
2
Таблица сопряженности факторов стоимости и
функционального назначения
|
|
Стоимость
1 м2, US$
|
Функциональное
назначение
|
Сумма
|
|
офисное
помещение
|
торговое
помещение
|
предприятие общественного
питания
|
предприятие
службы быта
|
|
[28; 68)
|
5
|
3
|
1
|
2
|
11
|
|
[68; 108)
|
19
|
16
|
4
|
7
|
46
|
|
[108; 148)
|
6
|
9
|
5
|
5
|
25
|
|
[148; 188]
|
1
|
5
|
2
|
0
|
8
|
|
Сумма
|
31
|
33
|
12
|
14
|
90
|
Для определения наличия и тесноты связи с результирующей переменной каждого
качественного факторного признака по таблицам сопряжённости были рассчитаны
коэффициенты Пирсона и Чупрова. Результаты приведены в таблице 3.
|
Таблица
3
Ранговые
коэффициенты корреляции
|
|
Название
коэффициента
|
Качественный фактор
|
|
Местоположение
|
Функциональное
назначение
|
|
Коэффициент Пирсона
|
0,464
|
0,360
|
|
Коэффициент Чупрова
|
0,282
|
0,207
|
Следует отметить, что максимальное значение коэффициента Пирсона для
таблицы сопряжённости размерности равно 0,866. Оно соответствует ситуации,
когда ненулевые значения находятся только на диагонали таблицы. Так как
рассчитанные коэффициенты Пирсона принимают приблизительно средние значения, то
можно сделать вывод, что между стоимостью 1 м2 рассматриваемой
доходной недвижимости и местоположением, а также функциональным назначением
объекта существует зависимость, тесноту которой можно оценить на среднем
уровне.
Для количественной оценки степени связи между результирующим признаком и
количественными факторами нами были рассчитаны коэффициенты парной корреляции
между соответствующими показателями (таблица 4).
|
Таблица
4
Парные коэффициенты
корреляции
|
|
№
|
Количественный
фактор
|
Коэффициент
корреляции
со стоимостью 1м2
общей внутренней
площади в US$
|
|
1
|
Доля подвала
|
−0,264
|
|
2
|
Возраст здания на момент оценки
|
0,243
|
|
3
|
Общая внутренняя площадь, м2
|
−0,237
|
|
4
|
Отношение наружной и внутренней площадей
|
0,215
|
|
5
|
Средняя высота помещения
|
0,186
|
|
6
|
Средневзвешенный физический износ
|
−0,477
|
|
7
|
Курс US$/грн. на дату оценки
|
0,052
|
|
8
|
Стоимость улучшение на 1 м2, US$
|
0,561
|
|
9
|
Коэффициент инженерного обеспечения
|
0,372
|
В результате анализа, для построения модели были отобраны переменные,
влияние которых на значение результирующей переменной было наиболее существенным.
Из количественных переменных таковыми оказались (в порядке убывания степени
связи): стоимость улучшения на 1 м2, величина средневзвешенного физического
износа, коэффициент инженерного обеспечения, доля подвала и возраст здания на
момент оценки. Также было принято решение, что оба качественных признака
(местоположение и функциональное назначение) оказывают значимое влияние на
результирующий показатель. В модель они вошли в виде двух наборов бинарных
переменных.
Построение модели производилось прямым пошаговым методом.
На первом этапе параллельно пошагово строились две модели с количественными
факторными переменными: аддитивная и полумультипликативная. На каждой итерации
пошагового метода выполнялись следующие действия: методом наименьших квадратов
оценивались значения параметров модели (с использованием пакета электронных
таблиц Microsoft Excel™), анализировались статистическая значимость
коэффициента при переменной, введенной на данной итерации, и значение
скорректированного коэффициента множественной детерминации. Если оказывалось,
что переменную стоит вводить в модель, то проводился анализ остатков на наличие
выбросов. Наблюдения, соответствующие остаткам, классифицированным как выбросы,
удалялись. Для оставшихся наблюдений оценивались значения коэффициентов
регрессии, после чего переходили к следующей итерации. В результате были
построены две модели, в которые вошли четыре количественные переменные (все,
которые предполагались изначально, кроме возраста здания на момент оценки).
Сравнение полученных моделей показало, что аддитивная модель имеет лучшие
показатели адекватности модели, в частности более высокий коэффициент множественной
детерминации, чем мультипликативная модель. В таблице 5 приведены результаты
регрессионного анализа для аддитивной модели с четырьмя количественными переменными.
Таким образом, результат выполнения
первого этапа можно представить в следующем виде:
|
ŷ =
|
96,13 −
|
74,35x1 +
|
0,48x2 −
|
7,33x3 +
|
20,74x4
|
|
(9,61)
|
(24,16)
|
(0,08)
|
(5,25)
|
(9,86)
|
где:
ŷ — стоимость 1 м2 внутренней площади помещения, US$;
x1 — средневзвешенный физический износ, в долях единицы;
x2 — стоимость улучшений на 1 м2 внутренней площади, US$;
x3 — доля площади подвала в общей площади;
x4 — коэффициент инженерного обеспечения.
В скобках под коэффициентами уравнения приведены соответствующие
среднеквадратические отклонения. Если стандартное отклонение превышает соответствующий
модуль оценки параметра, то это означает смещённость полученной оценки
параметра. В нашем случае полученные оценки оказались несмещёнными.
На втором этапе в модель включались качественные переменные. При этом
строились три модели: аддитивная, полумультипликативная и гибридная. Построение
производилось пошаговым методом, однако в отличие от первого этапа, дальнейшая
отбраковка выбросов не производилась.
Остановимся на построении гибридной модели. В эту модель количественные
переменные входят аддитивно, а качественные переменные — мультипликативно.
Для оценки значения регрессионных коэффициентов гибридной модели формировалась
искусственная факторная переменная — её значения вычислялись по уравнению
(6). Затем строилась мультипликативная модель, в которую в качестве первой
переменной включалась искусственная переменная, а затем, пошагово, все
качественные переменные. В результате была получена следующая гибридная модель:
ŷ =
(96,13 − 74,35x1 + 0,48x2 − 7,33x3 + 20,74x4) 1,0016 ·
(1,17)x5 · (1,18)x6 · (0,82)x7 · (0,87)x8 · (0,88)x9, (6)
где:
ŷ — стоимость 1 м2 внутренней площади помещения, US$;
x1 — средневзвешенный физический износ, в долях единицы;
x2 — стоимость улучшений на 1 м2 внутренней площади, US$;
x3 — доля площади подвала в общей площади;
x4 — коэффициент инженерного обеспечения.
x5 — принадлежность объекта к зоне 3;
x6 — принадлежность объекта к зоне 4;
x7 — функциональное назначение — офисные помещения;
x8 — функциональное назначение — торговые помещения;
x8 — функциональное назначение — предприятие общественного питания.
Никакая регрессионная модель не может быть точным отражением действительности.
Формализация реальных зависимостей всегда связана с упрощениями. Поэтому в
процессе анализа должно быть выявлено соответствие полученной модели реальной
зависимости, должны быть найдены пути улучшения модели и определены возможности
практической реализации достигнутых результатов.
2. Практическая часть
УСЛОВИЕ ЗАДАЧИ
Исходные данные представлены в таблице 5.
Таблица
5
Исходные
данные задачи
|
№ п/п
|
Показатель
|
Обозначение
|
Значение
|
|
1
|
t – критерий Стьюдента расчетный
|
t рас
|
2,941
|
|
2
|
F – критерий Фишера расчетный
|
F рас
|
16,48
|
|
3
|
t – критерий Стьюдента табличный
|
t таб
|
2,9
|
|
4
|
F – критерий Фишера табличный
|
F таб
|
15,4
|
|
5
|
Стандартное отклонение
|
S 1.2
|
0,021
|
|
6
|
Число наблюдений
|
N
|
10
|
|
7
|
Горизонт прогнозирования
|
T
|
12
|
|
8
|
а
|
а
|
-0,0003
|
|
9
|
В
|
в
|
0,012
|
РЕШЕНИЕ
1)
Устанавливаем величину
доверительных пределов прогноза при
сравнении расчетных и табличных значений критериев Стьюдента (t) из таблицы 1.
t рас
≥ t таб,
Табличное значение t
таб при условии, что n = N-2= 8, равно 2,9 (из таблиц критерия Стьюдента)
Тогда, 2,941≥
2,9 (при вероятности 0,98 )
Так как расчетное значение больше
табличного значения критерия Стьюдента, то предлагаемая модель прогноза соответствует
выбранному доверительному интервалу.
2)
Проверяем статистическую значимость модели сравнением
расчетного значения критерия Фишера и табличного значения.
F рас≥ F таб,
16,48≥
15,4 (при вероятности 0,98 )
Значит, модель прогноза статистически
значима и может применяться.
3)
Рассчитаем точечный прогноз:
У
(Т) = а+в*Т, (7)
Т = N +m = 10+2 = 12
Где m – величина упреждения (равна 2).
Значения а и в возьмем из таблицы 5.
Тогда, У (Т) = -0,0003+0,012*12 =
0,1437
Прогнозируемое значение показателя У в
12 м периоде от начала планирования равно 0,1437.
4)
Рассчитаем доверительные интервалы прогноза
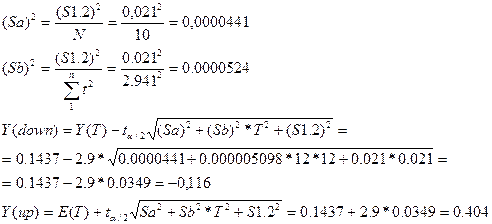
Выполненная оценка доверительных
пределов позволяет сделать вывод о том, что истинное значение прогнозируемого показателя будет
находиться в пределах от 0,04 до 0,25 с вероятностью 0,98, что свидетельствует
о низкой точности модели, используемой
для прогнозирования.
В таблице 6 отражена динамика значения
диапазона доверительных пределов
при изменении числа наблюдений N.
Таблица 6
Динамика диапазона доверительных пределов при изменении числа наблюдений
|
N
|
T
|
Y(T)
|
Sa2
|
Sb2
|
Ydown
|
Y up
|
|
10
|
12
|
0,1437
|
0,00004410
|
0,00005243757
|
-0,116
|
0,404
|
|
11
|
13
|
0,1557
|
0,00004009
|
0,00000006559
|
0,091
|
0,220
|
|
12
|
14
|
0,1677
|
0,00003675
|
0,00000007635
|
0,103
|
0,232
|
|
13
|
15
|
0,1797
|
0,00003392
|
0,00005960748
|
-0,162
|
0,521
|
|
14
|
16
|
0,1917
|
0,00003150
|
0,00000009537
|
0,127
|
0,256
|
|
15
|
17
|
0,2037
|
0,00002940
|
0,00000010438
|
0,139
|
0,269
|
|
16
|
18
|
0,2157
|
0,00002756
|
0,00000011472
|
0,150
|
0,281
|
|
17
|
19
|
0,2277
|
0,00002594
|
0,00000012250
|
0,162
|
0,293
|
|
18
|
20
|
0,2397
|
0,00002450
|
0,00006625203
|
-0,237
|
0,716
|
|
19
|
21
|
0,2517
|
0,00002321
|
0,00000013573
|
0,185
|
0,318
|
|
20
|
22
|
0,2637
|
0,00002205
|
0,00000014579
|
0,197
|
0,331
|
ОТВЕТ
Истинное значение прогнозируемого
показателя будет находиться в пределах от -0,116 до 0,404 с вероятностью 0,98.
Список литературы
1. Айвазян С.А.,
Енюков И.С., Мешалкин Л.Д. «Прикладная статистика: исследование
зависимостей. / Справочное издание под ред. Айвазяна С.А. — М.: Финансы и
статистика, 1985. — 471 с.
2. Айвазян С.А.,
Енюков И.С., Мешалкин Л.Д. «Прикладная статистика: Основы моделирования
и первичная обработка данных». / Справочное издание под ред. Айвазяна С.А. —
М.: Финансы и статистика, 1983. — 471 с.
3. Грибовский С.В.
«Оценка доходной недвижимости». — СПб: «Питер», 2001. — 336 с.
4. Доугерти К.
«Введение в эконометрику» / Пер. с англ. — М.: «ИНФРА», 2001. — 402
с.
5. «Оценка
стоимости предприятия (бизнеса): Учебное пособие» / Под ред. Абдулаева Н.А.,
Колайко Н.А. — М.: «ЭКМОС», 2000. — 352 с.
6. «Оценка
стоимости предприятия (бизнеса): Учебное пособие» / Под ред. Абдулаева Н.А.,
Колайко Н.А. — М.: «ЭКМОС», 2000. — 352 с.
7. Тюрин Ю.Н.,
Макаров А.А. «Статистический анализ данных на компьютере» / Под. ред.
Фигурнова В.Э. — М.: «ИНФРА», 1998. — 528 с.
8. Фёрстер Э.,
Рёнц Б. «Методы корреляционного и регрессионного анализа: Руководство для
экономистов». — М.: «Финансы и статистика», 1983. — 302 с.
9. «Эконометрика:
Учебник» / Под. ред. Елисеевой И.И. — М.: «Финансы и статистика»,
2001. — 344 с.