Задача 1
вариант 4
По
предприятиям легкой промышленности региона получена информация (табл.1),
характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (Х, млн.
руб.).
Таблица 1
|
X
|
36
|
28
|
43
|
52
|
51
|
54
|
25
|
37
|
51
|
29
|
|
Y
|
104
|
77
|
117
|
137
|
143
|
144
|
82
|
101
|
132
|
77
|
Требуется:
1. Найти параметры уравнения линейной регрессии, дать
экономическую интерпретацию коэффициента регрессии.
2. Вычислить
остатки; найти остаточную сумму квадратов; оценить дисперсию остатков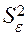 
; построить график остатков.
3. Проверить
выполнение предпосылок МНК.
4. Осуществить
проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (a
= 0,05).
5. Вычислить
коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (a
= 0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о
качестве модели.
6. Осуществить
прогнозирование среднего значения показателя Y при уровне значимости a
=0,1, если прогнозное значение фактора Х составит 80% от его максимального
значения.
7. Представить
графически: фактические и модельные значения Y, точки прогноза.
8. Составить
уравнение нелинейной регрессии:
·
гиперболической;
·
степенной;
·
показательной.
Привести
графики построенных уравнений регрессии.
9. Для указанных моделей найти коэффициенты детерминации
и средние относительные ошибки аппроксимации. Сравнить модели по этим
характеристикам и сделать вывод.
Решение:
1. Уравнение
линейной регрессии имеет вид: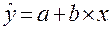 
.
Значения
параметров a и b линейной
модели определим, используя данные таблицы 2.
Таблица 2
|
№ п/п
|
x
|
y
|
y*x
|
x*x
|
yi - yср
|
(yi - yср)2
|
xi - xср
|
(xi - xср)2
|
ŷ=а+b*xi
|
|
1
|
36
|
104
|
3744
|
1296
|
-7,40
|
54,76
|
-4,6
|
21,16
|
100,36
|
|
2
|
28
|
77
|
2156
|
784
|
-34,40
|
1183,36
|
-12,6
|
158,76
|
81,16
|
|
3
|
43
|
117
|
5031
|
1849
|
5,60
|
31,36
|
2,4
|
5,76
|
117,16
|
|
4
|
52
|
137
|
7124
|
2704
|
25,60
|
655,36
|
11,4
|
129,96
|
138,76
|
|
5
|
51
|
143
|
7293
|
2601
|
31,60
|
998,56
|
10,4
|
108,16
|
136,36
|
|
6
|
54
|
144
|
7776
|
2916
|
32,60
|
1062,76
|
13,4
|
179,56
|
143,56
|
|
7
|
25
|
82
|
2050
|
625
|
-29,40
|
864,36
|
-15,6
|
243,36
|
73,96
|
|
8
|
37
|
101
|
3737
|
1369
|
-10,40
|
108,16
|
-3,6
|
12,96
|
102,76
|
|
9
|
51
|
132
|
6732
|
2601
|
20,60
|
424,36
|
10,4
|
108,16
|
136,36
|
|
10
|
29
|
77
|
2233
|
841
|
-34,40
|
1183,36
|
-11,6
|
134,56
|
83,56
|
|
Сумма
|
406
|
1114
|
47876
|
17586
|
0,00
|
6566,40
|
0,00
|
1102,40
|
|
|
Среднее
|
40,6
|
111,4
|
4787,6
|
1758,6
|
|
|
|
|
|
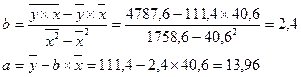
Уравнение линейной регрессии имеет вид: ŷ = 13,96
+ 2,4´ х
Интерпретировать можно лишь знак при параметре а. В этой задаче, а>0, следовательно, относительное изменение результата
происходит медленнее, чем изменение фактора. Иными словами, вариация результата
меньше вариации фактора – коэффициент вариации по фактору х выше коэффициента вариации для результата у: Vx >Vy.
2. Значения
остатков еi рассчитаны в
таблице 3.Остаток еi
– расхождение между фактическим и спрогнозированным значениями величины у. Квадратный корень из этой величины
называется стандартной ошибкой оценки.
Таблица 3
|
ei = yi
- ŷ
|
|ei/yi|*100%
|
ei2
|
ei-ei-1
|
(ei-ei-1)2
|
ei*ei-1
|
|
3,64
|
3,50
|
13,25
|
-
|
-
|
-
|
|
-4,16
|
5,40
|
17,31
|
-7,8
|
60,84
|
-15,1424
|
|
-0,16
|
0,14
|
0,03
|
4
|
16
|
0,6656
|
|
-1,76
|
1,28
|
3,10
|
-1,6
|
2,56
|
0,2816
|
|
6,64
|
4,64
|
44,09
|
8,4
|
70,56
|
-11,6864
|
|
0,44
|
0,31
|
0,19
|
-6,2
|
38,44
|
2,9216
|
|
8,04
|
9,80
|
64,64
|
7,6
|
57,76
|
3,5376
|
|
-1,76
|
1,74
|
3,10
|
-9,8
|
96,04
|
-14,1504
|
|
-4,36
|
3,30
|
19,01
|
-2,6
|
6,76
|
7,6736
|
|
-6,56
|
8,52
|
43,03
|
-2,2
|
4,84
|
28,6016
|
|
0,00
|
38,64
|
207,74
|
|
353,80
|
2,70
|
|
|
3,86
|
|
|
|
|
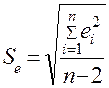
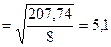
Остаточная
сумма квадратов отклонений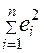 
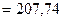
Стандартная
ошибка оценки Se
= 5,1
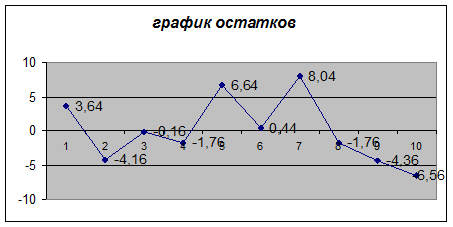
Рис.1. График остатков
3. Независимость
остатков проверяется с помощью критерия Дарбина – Уотсона.
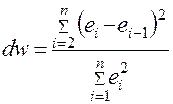
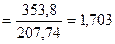
Автокорреляция случайной составляющей
нарушает одну из предпосылок нормальной линейной модели регрессии.
Значение статистики dw найдено по
промежуточным данным в таблице 3. Оценки, полученные по критерию, являются не точными,
а интервальными. Верхние (d2) и нижние (d1) критические значения для уровня значимости a=0,05, k = 1, n=10 берем из таблицы d1=1,08 и d2=1,36.
Перед сравнением с табличными значениями dw критерий следует преобразовать по формуле dw'= 4 – dw = 4- 1,703= 2,3. Таким образом, получается, что dw>2, что свидетельствует о наличии отрицательной
корреляции.
Установив наличие автокорреляции остатков, переходят к
улучшению модели. В частности, можно воспользоваться первым коэффициентом
автокорреляции
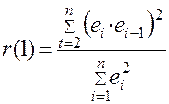
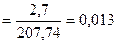
Для принятия решения о наличии или отсутствии
автокорреляции в исследуемом ряду фактическое значение коэффициента
автокорреляции r(1) сопоставляется с табличным
значением для 5%-ного уровня значимости. r(1)табл. =0,36> 0,013, следовательно, гипотеза об отсутствии
автокорреляции может быть принята.
4. Значимость
коэффициентов уравнения регрессии оценим с использованием t-критерия Стьюдента.
Значения t-критерия
вычислим по формулам для соответствующих коэффициентов регрессии.
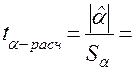
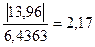
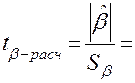
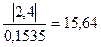
Коэффициент Стьюдента t для m = n- 2 = 8 степеней свободы и уровня значимости a=0,05 равен 2,3060.
Так как t – расчетное с
(n – 2)
степенями свободы в обоих случаях превышает t – табличное при заданном уровне значимости, то оба
коэффициента регрессии считаются значимыми.
5. Рассчитаем
коэффициент детерминации:
.
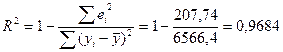Он показывает долю вариации результативного признака, находящегося
под воздействием изучаемых факторов, т.е. определяет, какая доля вариации
признака Y учтена в модели и обусловлена
влиянием на него факторов.
Чем ближе R2 к 1, тем лучше качество модели.
Таким образом, вариация результата Y (объема выпуска продукции) на 96,84% объясняется
вариацией фактора X (объемом капиталовложений).
Качество модели очень хорошее, линейная модель хорошо аппроксимирует исходные
данные, и ею можно воспользоваться для прогноза значений результативного
признака.
Для проверки значимости модели регрессии используется F-критерий Фишера:
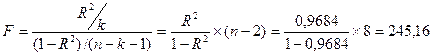
F>Fтабл= 5,32 для a=0,05, k1 =m =1, k2 = n-m-1 = n-2 =8.
Уравнение регрессии с вероятностью 0,95 в целом
статистически значимое, т.к. F>Fтабл..
Определим среднюю относительную ошибку аппроксимации:
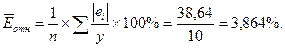
В среднем значение ŷ
для степенной модели отличаются от фактических значений на 3,864%. Чем меньше
рассеяние эмпирических точек вокруг теоретической линии регрессии, тем меньше
средняя ошибка аппроксимации. Так как ошибка аппроксимации данной модели меньше
7%, то это свидетельствует о хорошем качестве модели.
6. Пусть
хпрогн= 0,8*хmax =
0,8*54= 43,2, сделаем прогноз для среднего значения показателя Y при уровни значимости a=0,1.
Стандартную ошибку предсказываемого по линии регрессии
значения найдем по формуле:
;
.
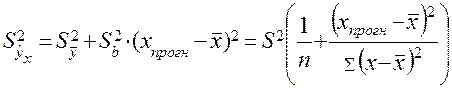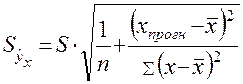Дана
формула характеризует ошибку положения линии регрессии. Величина стандартной ошибки
предсказываемого среднего значения у при заданном значении хпрогн достигает минимума при хпрогн = х,
и возрастает по мере того, как «удаляется» от х в любом направлении.
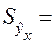
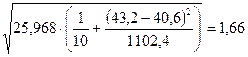
Для прогнозируемого значения ŷх 95%-ные
доверительные интервалы при заданном хпрогн определяются выражением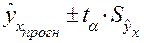 
, т.е.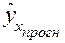 
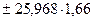или ±43,11, при значении коэффициента Стьюдента ta=25,968 для m=8
степеней свободы и уровня значимости 0,1.
Прогнозное значение составит упрогн = 13,96
+2,4 ∙ 43,2 = 117,64, которое представляет собой точечный прогноз.
Прогноз линии регрессии в интервале составит:
117,64 - 43,11 £ 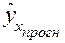£ 117,64+43,11 т.е.
74,53
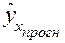£ £ 160,75.
7. Построим график
фактических, модельных значений Y,
точек прогноза.
Для
линейной модели регрессии доверительный интервал рассчитывается следующим
образом. Оценивается величина отклонения от линии регрессии (обозначим ее U):
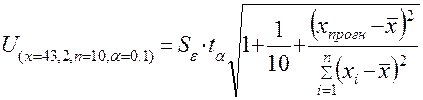
Коэффициент
Стьюдента ta
для m=8
степеней свободы (m=n-1) и уровня значимости
0,1 равен 1,8595. Тогда:
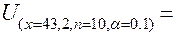
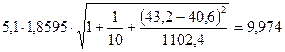
Таким образом, прогнозное значение 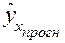= 117,64 будет находиться между верхней границей,
равной 117,64+9,974 = 127,6, и нижней границей, равной 117,64-9,974 = 107,7.
График исходных данных и результаты моделирования приведены на рис. 2.
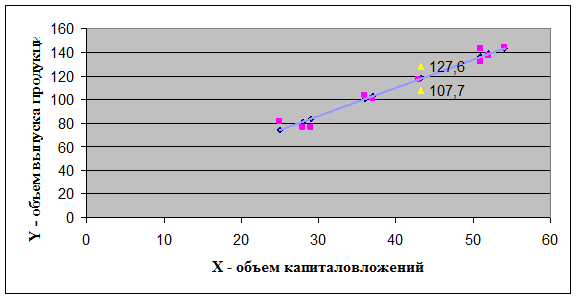
Рис.2. График модели парной регрессии зависимости объема
выпуска продукции от объема капиталовложения.
8. Составим
уравнение нелинейной регрессии:
Построение
гиперболической функции.
Уравнение гиперболической функции: ŷ = a+b/x
Произведем
линеаризацию модели путем замены Х = 1/х.
В
результате получим линейное уравнение: ŷ
= a+b ∙Х
Рассчитаем
его параметры по данным таблицы 4:
Таблица 4
|
№ п/п
|
x
|
y
|
Х
|
уХ
|
Х2
|
у-уср
|
(у-уср)2
|
ŷ=a+b*Xi
|
ei = yi - ŷ
|
(y-ŷ)2
|
|ei/yi|*100%
|
|
1
|
36
|
104
|
0,0278
|
2,8889
|
0,0008
|
-7,4
|
54,76
|
107,26
|
-3,2645
|
10,6567
|
3,1389
|
|
2
|
28
|
77
|
0,0357
|
2,7500
|
0,0013
|
-34,4
|
1183,36
|
81,12
|
-4,1224
|
16,9945
|
5,3538
|
|
3
|
43
|
117
|
0,0233
|
2,7209
|
0,0005
|
5,6
|
31,36
|
122,16
|
-5,1593
|
26,6188
|
4,4097
|
|
4
|
52
|
137
|
0,0192
|
2,6346
|
0,0004
|
25,6
|
655,36
|
135,42
|
1,5826
|
2,5046
|
1,1552
|
|
5
|
51
|
143
|
0,0196
|
2,8039
|
0,0004
|
31,6
|
998,56
|
134,18
|
8,8246
|
77,8739
|
6,1711
|
|
6
|
54
|
144
|
0,0185
|
2,6667
|
0,0003
|
32,6
|
1062,76
|
137,76
|
6,2365
|
38,8939
|
4,3309
|
|
7
|
25
|
82
|
0,0400
|
3,2800
|
0,0016
|
-29,4
|
864,36
|
67,01
|
14,9943
|
224,8277
|
18,2857
|
|
8
|
37
|
101
|
0,0270
|
2,7297
|
0,0007
|
-10,4
|
108,16
|
109,74
|
-8,7374
|
76,3415
|
8,6509
|
|
9
|
51
|
132
|
0,0196
|
2,5882
|
0,0004
|
20,6
|
424,36
|
134,18
|
-2,1754
|
4,7323
|
1,6480
|
|
10
|
29
|
77
|
0,0345
|
2,6552
|
0,0012
|
-34,4
|
1183,36
|
85,18
|
-8,1790
|
66,8954
|
10,6220
|
|
Сумма
|
406
|
1114
|
0,2652
|
27,7182
|
0,0076
|
|
6566,4
|
1114
|
0,0000
|
546,3394
|
63,7661
|
|
Среднее
|
40,6
|
111,4
|
0,0265
|
2,7718
|
0,0008
|
|
|
|
|
|
6,3766
|
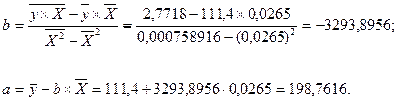
Получим следующее уравнение гиперболической модели:
ŷ= 198,76-3293,9/х.
Построение степенной функции.
Уравнение степенной модели имеет вид: ŷ = a+xb.
Для построения этой модели необходимо произвести
линеаризацию переменных. Для этого произведем логарифмирование обеих частей
уравнения: lg ŷ = lg a +b lg x.
Таблица 5
|
№ п/п
|
Факт Y(t)
|
lg (Y)
|
Переменная Х(t)
|
lg(x)
|
|
1
|
104
|
2,0170
|
36
|
1,5563
|
|
2
|
77
|
1,8865
|
28
|
1,4472
|
|
3
|
117
|
2,0682
|
43
|
1,6335
|
|
4
|
137
|
2,1367
|
52
|
1,7160
|
|
5
|
143
|
2,1553
|
51
|
1,7076
|
|
6
|
144
|
2,1584
|
54
|
1,7324
|
|
7
|
82
|
1,9138
|
25
|
1,3979
|
|
8
|
101
|
2,0043
|
37
|
1,5682
|
|
9
|
132
|
2,1206
|
51
|
1,7076
|
|
10
|
77
|
1,8865
|
29
|
1,4624
|
|
Сумма
|
1114
|
20,3473
|
406
|
15,9290
|
|
Среднее
|
111,4
|
2,0347
|
40,6
|
1,5929
|
Обозначим Y= lg ŷ, X= lg x, А= lg а. Тогда уравнение примет вид Y= A+ bX – линейное уравнение регрессии.
Рассчитаем его параметры, используя данные табл. 6.
Таблица 6
|
№ п/п
|
y
|
Y
|
x
|
X
|
YX
|
X2
|
ŷ=10A ´
xb=
=4,661´ x 0,8577
|
ei = yi - ŷ
|
|ei/yi|*100%
|
ei2
|
|
1
|
104
|
2,0170
|
36
|
1,5563
|
3,1391
|
2,4221
|
100,773
|
3,23
|
3,10
|
10,41
|
|
2
|
77
|
1,8865
|
28
|
1,4472
|
2,7301
|
2,0943
|
81,233
|
-4,23
|
5,50
|
17,92
|
|
3
|
117
|
2,0682
|
43
|
1,6335
|
3,3783
|
2,6682
|
117,363
|
-0,36
|
0,31
|
0,13
|
|
4
|
137
|
2,1367
|
52
|
1,7160
|
3,6666
|
2,9447
|
138,141
|
-1,14
|
0,83
|
1,30
|
|
5
|
143
|
2,1553
|
51
|
1,7076
|
3,6804
|
2,9158
|
135,859
|
7,14
|
4,99
|
50,99
|
|
6
|
144
|
2,1584
|
54
|
1,7324
|
3,7391
|
3,0012
|
142,686
|
1,31
|
0,91
|
1,73
|
|
7
|
82
|
1,9138
|
25
|
1,3979
|
2,6754
|
1,9542
|
73,708
|
8,29
|
10,11
|
68,75
|
|
8
|
101
|
2,0043
|
37
|
1,5682
|
3,1432
|
2,4593
|
103,170
|
-2,17
|
2,15
|
4,71
|
|
9
|
132
|
2,1206
|
51
|
1,7076
|
3,6210
|
2,9158
|
135,859
|
-3,86
|
2,92
|
14,89
|
|
10
|
77
|
1,8865
|
29
|
1,4624
|
2,7588
|
2,1386
|
83,715
|
-6,71
|
8,72
|
45,09
|
|
Сумма
|
1114
|
20,3473
|
406
|
15,9290
|
32,5320
|
25,5141
|
|
1,49
|
39,55
|
215,92
|
|
Среднее
|
111,4
|
2,0347
|
40,6
|
1,5929
|
3,2532
|
2,5514
|
|
|
3,96
|
21,59
|
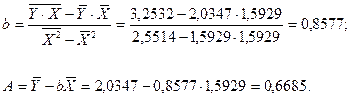
Уравнение регрессии будет иметь вид: Y= 0,6685+0,8577 ´ Х.
Перейдем к исходным переменным х и у, выполнив
потенцирование данного уравнения:
ŷ = 100,6685 ´ х0,8577.
Получим уравнение степенной модели регрессии:
ŷ = 4,6611´ х0,8577.
Построение показательной функции.
Уравнение показательной кривой: ŷ =а ∙ bх.
Для построения этой модели необходимо произвести
линеаризацию переменных. Для этого осуществим логарифмирование обеих частей
уравнения: lg ŷ = lg a + lg x ∙ b.
Обозначим Y= lg ŷ, B= lg b, A= lg a.
Получим
линейное уравнение регрессии: Y = A+B∙x.
Рассчитаем
его параметры, используя данные табл. 7.
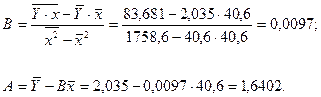
Уравнение
будет иметь вид: Y= 1,6402 – 0,0097х
Перейдем
к исходным переменным х и у, выполнив потенцирование данного уравнения:
ŷ =101,6402´(100,0097)х = 43,68´ 1,023х.
Таблица 7
|
№ п/п
|
y
|
Y
|
x
|
Yx
|
x2
|
Y-Yср
|
(Y-Yср)2
|
x-xср
|
(x-xср)2
|
ŷ=10A´(10B)x=
=43,68´1,023x
|
ei = yi
- ŷ
|
ei2
|
|ei/yi|*100%
|
|
1
|
104
|
2,017
|
36
|
72,613
|
1296
|
-0,018
|
0,0003
|
-4,6
|
21,16
|
99,039
|
4,961
|
24,6133
|
4,7704
|
|
2
|
77
|
1,886
|
28
|
52,822
|
784
|
-0,148
|
0,0220
|
-12,6
|
158,76
|
82,566
|
-5,566
|
30,9785
|
7,2284
|
|
3
|
117
|
2,068
|
43
|
88,932
|
1849
|
0,033
|
0,0011
|
2,4
|
5,76
|
116,127
|
0,873
|
0,7613
|
0,7458
|
|
4
|
137
|
2,137
|
52
|
111,109
|
2704
|
0,102
|
0,0104
|
11,4
|
129,96
|
142,500
|
-5,500
|
30,2526
|
4,0148
|
|
5
|
143
|
2,155
|
51
|
109,922
|
2601
|
0,121
|
0,0145
|
10,4
|
108,16
|
139,296
|
3,704
|
13,7165
|
2,5899
|
|
6
|
144
|
2,158
|
54
|
116,552
|
2916
|
0,124
|
0,0153
|
13,4
|
179,56
|
149,131
|
-5,131
|
26,3234
|
3,5629
|
|
7
|
82
|
1,914
|
25
|
47,845
|
625
|
-0,121
|
0,0146
|
-15,6
|
243,36
|
77,121
|
4,879
|
23,8032
|
5,9498
|
|
8
|
101
|
2,004
|
37
|
74,160
|
1369
|
-0,030
|
0,0009
|
-3,6
|
12,96
|
101,317
|
-0,317
|
0,1003
|
0,3136
|
|
9
|
132
|
2,121
|
51
|
108,149
|
2601
|
0,086
|
0,0074
|
10,4
|
108,16
|
139,296
|
-7,296
|
53,2377
|
5,5276
|
|
10
|
77
|
1,886
|
29
|
54,708
|
841
|
-0,148
|
0,0220
|
-11,6
|
134,56
|
84,465
|
-7,465
|
55,7240
|
9,6946
|
|
Сумма
|
1114
|
20,347
|
406
|
836,813
|
17586
|
|
0,1085
|
|
1102,4
|
|
-16,859
|
259,5109
|
44,3977
|
|
Среднее
|
111,4
|
2,035
|
40,6
|
83,681
|
1758,6
|
|
|
|
110,24
|
|
|
|
4,4398
|
Графики построенных уравнений:
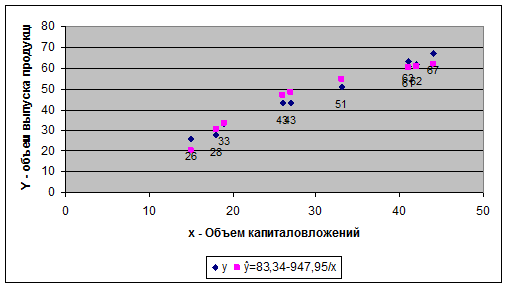
Рис.3. График гиперболической функции
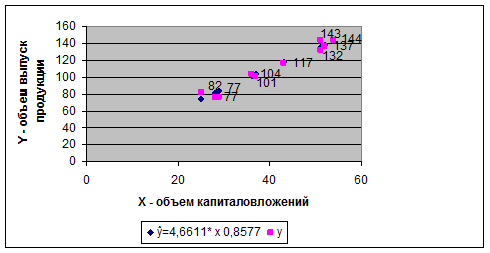
Рис.4. график степенной функции
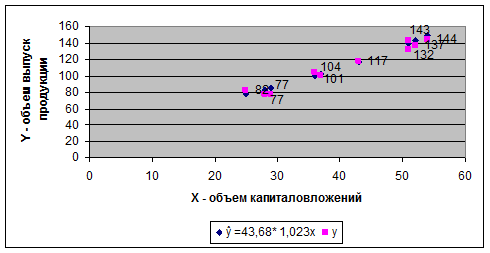
Рис.5. График степенной функции
9. Значения коэффициента детерминации и средней
относительной ошибки аппроксимации для рассмотренных моделей находим из
расчетных значений таблиц 4, 6, 7. Для выбора лучшей модели построим сводную
таблицу результатов.
|
Модель
|
параметры
|
|
Коэффициент
детерминации
|
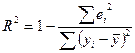
Средняя
относительная ошибка
|
|
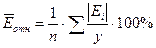
Гиперболическая
|
0,917
|
6,38
|
|
Степенная
|
0,967
|
3,96
|
|
Показательная
|
0,961
|
4,44
|
Коэффициент детерминации показывает, какая доля
вариации признака Y учтена в модели и обусловлена
влиянием на него факторов. Чем ближе R к 1,
тем лучше качество модели. Значит, по этому параметру лучшей моделью является
степенная (R2 = 0,967).
Средняя относительная ошибка аппроксимации показывает,
на сколько в среднем расчетные значения ŷ для модели отличаются от
фактических значений. Чем меньше рассеяние эмпирических точек вокруг
теоретической линии регрессии, тем меньше средняя ошибка аппроксимации. Значит,
по этому параметру лучшей моделью является степенная (Ēотн =
3,96).
Задача 2а
вариант 3
Для каждого варианта даны по две СФМ, которые заданы в
виде матриц коэффициентов модели. Необходимо записать системы одновременных
уравнений и проверить обе системы на идентифицируемость.
Таблица 1
|
Номер
уравнения
|
переменные
|
|
у1
|
у2
|
у3
|
х1
|
х2
|
х3
|
х4
|
|
1
|
-1
|
0
|
b13
|
a11
|
a12
|
0
|
a14
|
|
2
|
b21
|
-1
|
0
|
a21
|
a22
|
0
|
a24
|
|
3
|
b31
|
b32
|
-1
|
0
|
0
|
a33
|
a34
|
Используя данные таблицы, составим следующую
структурную модель:
y1 = b13у3 + a11x1 + a12x2
+ a14x4 ;
y2 = b21у1 + a21x1 + a22x2
+ a24x4 ;
y3 = b31у1 + b32у2 + a33x3
+ a34x4.
Проверим каждое уравнение системы на выполнение
необходимого и достаточного условия идентификации.
В первом уравнении две эндогенные переменные: y1 и y3 (Н = 2). В нем отсутствует одна экзогенная переменная х3 (D = 1). Необходимое условие идентификации D + 1 = H выполнено.
Для проверки на достаточное условие
составим матрицу из коэффициентов при переменных у2 и х2,
которые отсутствуют в первом уравнении (табл. 1а). В первом столбце показано,
что коэффициенты при переменных у2 и х3 взяты из
уравнений 2 и 3 системы. Во втором уравнении при переменной у2 коэффициент
равен -1, при переменной х3 коэффициент
равен 0. В третьем уравнении при у2 коэффициент равен b32. При переменной х3 коэффициент равен а33.
Определитель представленной в табл.1а матрицы не равен нулю. Значит,
достаточное условие выполнено, и первое уравнение идентифицируемо.
Таблица 1а
Матрица,
составленная из коэффициентов
при
переменных у2 и х3
|
Уравнения,
из которых
взяты
коэффициенты
при
переменных
|
переменные
|
|
у2
|
х3
|
|
2
|
-1
|
0
|
|
3
|
b32
|
а33
|
Во втором уравнении две эндогенные переменные: у1 и у2
(Н = 2). В нем отсутствует одна экзогенная
переменная х3 (D = 1).
Необходимое условие идентификации D + 1 = H выполнено.
Для проверки на достаточное условие составим матрицу
из коэффициентов при переменных у3 и х3 (табл. 1б). В
первом столбце показано, что коэффициенты при экзогенных переменных у3
и х3 взяты из уравнений 1 и 3 системы. В первом уравнении эти
переменные присутствуют и коэффициенты при них равны b13 и 0
соответственно. В третьем уравнении при у3- -1. При переменной х3 коэффициент
равен а33. Определитель представленной в табл.1б матрицы не равен
нулю. Значит, достаточное условие выполнено, и второе уравнение
идентифицируемо.
Таблица 1б
Матрица,
составленная из коэффициентов
при
переменных у3 и х3
|
Уравнения,
из которых
взяты
коэффициенты
при
переменных
|
переменные
|
|
у3
|
х3
|
|
1
|
b13
|
0
|
|
3
|
-1
|
а33
|
В третьем уравнении - три эндогенные переменные: y1, y2 и
y3 (Н = 3). В нем отсутствуют две экзогенные
переменные - х1, х2 (D = 2).
Необходимое условие идентификации D + 1 = H выполнено.
Согласно таблице 1в определитель
матрицы не равен нулю. Значит достаточное уравнение выполнено, и третье
уравнение идентифицируемо.
Таблица 1в
Матрица,
составленная из коэффициентов
при
переменных х1 и х2
|
Уравнения,
из которых
взяты
коэффициенты
при
переменных
|
переменные
|
|
х1
|
х2
|
|
1
|
а11
|
а12
|
|
2
|
а21
|
а22
|
ВЫВОД: Так как все три уравнения системы идентифицируемы,
следовательно, вся система идентифицируема.
Задача 2б
вариант 9
Необходимо записать системы одновременных уравнений и
проверить обе системы на идентифицируемость.
Таблица 2
|
Номер
уравнения
|
переменные
|
|
у1
|
у2
|
у3
|
х1
|
х2
|
х3
|
х4
|
|
1
|
-1
|
b12
|
b13
|
a11
|
a12
|
0
|
0
|
|
2
|
b21
|
-1
|
b23
|
0
|
0
|
а23
|
a24
|
|
3
|
b31
|
b32
|
-1
|
0
|
0
|
а33
|
а34
|
Используя данные таблицы, составим следующую
структурную модель:
y1 = b12y2
+ b13y3 + a11x1 + a12x2;
y2 = b21y1
+ b 23у3 + a23x3
+a24x4;
y3 = b31y1 + b32y2
+ a33x3 + a34x4.
Проверим каждое уравнение системы на выполнение
необходимого и достаточного условия идентификации.
В первом уравнении три эндогенные переменные: у1, у2 и у3 (Н = 3). В нем
отсутствует две экзогенные переменные х3, х4 (D = 2).
Необходимое условие идентификации D + 1 = H выполнено.
Следовательно, уравнение точно идентифицируемо.
Согласно таблице 2а определитель матрицы не равен нулю. Значит достаточное условие выполнено,
и первое уравнение идентифицируемо.
Таблица 2а
Матрица, составленная
из коэффициентов
при
переменных х3 и х4
|
Уравнения,
из которых
взяты
коэффициенты
при
переменных
|
переменные
|
|
х3
|
х4
|
|
2
|
a23
|
a24
|
|
3
|
a33
|
a34
|
Во втором уравнении три эндогенные переменные: у1, у2 и у3 (Н = 3). В нем отсутствуют две экзогенные переменные х1
и х2 (D = 2).
Необходимое условие идентификации D + 1 = H выполнено.
Определитель представленной в табл.2б матрицы равен
нулю. Значит, достаточное условие не выполнено, и второе уравнение не дентифицируемо.
Таблица 2б
Матрица,
составленная из коэффициентов
при
переменных х1 и х2
|
Уравнения,
из которых
взяты
коэффициенты
при
переменных
|
переменные
|
|
х1
|
х2
|
|
1
|
а11
|
а12
|
|
3
|
0
|
0
|
В третьем уравнении три эндогенные переменные: y1, y2 и y3 (Н = 3). В нем отсутствует две экзогенные
переменные х1 И х2 (D = 2).
Необходимое условие идентификации D + 1 = H выполнено.
Определитель матрицы равен нулю. Значит, достаточное
уравнение не выполнено, и третье уравнение нельзя считать идентифицируемым.
Таблица 2в
Матрица,
составленная из коэффициентов
при
переменных х1 и х2
|
Уравнения,
из которых
взяты
коэффициенты
при
переменных
|
переменные
|
|
х1
|
х2
|
|
1
|
а11
|
а12
|
|
2
|
0
|
0
|
ВЫВОД: Второе и третье уравнения не идентифицируемы,
следовательно, вся система не идентифицируема.
Задача 2в
вариант 2
По данным таблицы, используя косвенный метод
наименьших квадратов, построить структурную форму модели вида:
у1 = а01 + b12y2 + a11x1 + e1,
y2 = a02 + b21y1 + a22x2 +e2.
Для построения модели мы располагаем информацией,
представленной в таблице 1.
Таблица 1
Фактические данные для построения модели
|
n
|
y1
|
y2
|
x1
|
x2
|
|
1
|
28,3
|
51,7
|
7
|
12
|
|
2
|
4,4
|
11,5
|
1
|
1
|
|
3
|
33,1
|
64,6
|
10
|
14
|
|
4
|
14,6
|
38,4
|
9
|
4
|
|
5
|
35,9
|
64,1
|
7
|
17
|
|
6
|
39,5
|
55,0
|
1
|
20
|
|
Сумма
|
155,8
|
285,3
|
35
|
68
|
|
Среднее
|
25,967
|
47,55
|
5,833
|
11,333
|
Структурную модель преобразуем в приведенную форму
модели:
у1 = d11x1 + d12x2 + u1;
y2 = d21x1 + d22x2 + u2.
где u1 и u2 – случайные ошибки.
Для каждого уравнения приведенной формы при расчете
коэффициентов d можно применить МНК.
Для упрощения расчетов можно работать с отклонениями
от средних уровней у = у - уср и х = х - хср (уср и хср – средние значения).
Преобразованные таким образом данные табл.1 сведены в таблице 2. Здесь же
показаны промежуточные расчеты, необходимые для определения коэффициентов dik. Переменные, означающие отклонение от средних
значений, изображаются далее жирным шрифтом и курсивом.
Таблица 2
Преобразованные данные
для построения
приведенной формы модели
|
n
|
y1
|
y2
|
x1
|
x2
|
y1*x1
|
x12
|
x1*x2
|
y1*x2
|
y2*x1
|
y2*x2
|
x22
|
|
1
|
28,3
|
51,7
|
7
|
12
|
198,1
|
49
|
84
|
339,6
|
361,9
|
620,4
|
144
|
|
2
|
4,4
|
11,5
|
1
|
1
|
4,4
|
1
|
1
|
4,4
|
11,5
|
11,5
|
1
|
|
3
|
33,1
|
64,6
|
10
|
14
|
331,0
|
100
|
140
|
463,4
|
646,0
|
904,4
|
196
|
|
4
|
14,6
|
38,4
|
9
|
4
|
131,4
|
81
|
36
|
58,4
|
345,6
|
153,6
|
16
|
|
5
|
35,9
|
64,1
|
7
|
17
|
251,3
|
49
|
119
|
610,3
|
448,7
|
1089,7
|
289
|
|
6
|
39,5
|
55,0
|
1
|
20
|
39,5
|
1
|
20
|
790,0
|
55,0
|
1100,0
|
400
|
|
Сумма
|
155,8
|
285,3
|
35
|
68
|
955,7
|
281
|
400
|
2266,1
|
1868,7
|
3879,6
|
1046
|
|
Среднее
|
25,967
|
47,55
|
5,833
|
11,333
|
|
|
|
|
|
|
|
Для нахождения коэффициентов d1k первого
приведенного уравнения можно использовать следующую систему нормальных
уравнений: Первое уравнение
Sy1x1
= d11 Sx12
+ d12Sx1x2;
Sy1x2
= d11 Sx1x2
+ d12 Sx22.
Подставляя рассчитанные в таблице 2 значения сумм,
получаем:
955,7 = 281d11 + 400d12;
2266,1 = 400d11 + 1046d12.
Решение этих уравнений дает значения d11 =
0,696 и d12 = 1,9. Первое
уравнение приведенной формы модели примет вид:
у1 = 0,696х1 + 1,9х2
+ u1.
Для нахождения коэффициентов d2k
второго приведенного уравнения можно использовать следующую систему нормальных
уравнений:
Sу2х1 = d21 Sx12 + d22 Sx1x2;
Sy2x2 = d21 Sx1x2 + d22
Sx22.
Подставляя рассчитанные в таблице 2 значения сумм,
получаем:
|
1868,700
|
=
|
281,00
|
d21
|
+
|
400,00
|
d22
|
|
3879,600
|
=
|
400,00
|
d21
|
+
|
1046,00
|
d22
|
Решение этих уравнений дает значения d21 = 3,008 и
d22 =
2,559. Второе уравнение приведенной формы модели примет вид:
у2 = 3,008х1 + 2,559х2
+ u2.
Для перехода от приведенной формы к структурной форме
модели найдем х2 из второго уравнения приведенной формы модели:
х2 = (у2 – 3,008х1)/2,559.
Подставим это выражение в первое уравнение приведенной
модели, найдем структурное уравнение:
у1 = 0,696х1 + 1,9*(у2
– 3,008х1)/2,559
= 0,696х1
+ 0,743у2 - 2,234х1 = 0,743у2 -1,538х1.
Таким образом, b12 =
0,743; a11 = -1,538
Найдем х1 из первого уравнения приведенной
формы модели:
х1 = (у1 – 1,9х2)/0,696.
Подставим это выражение во второе уравнение
приведенной модели, найдем структурное уравнение:
у2 = 2,559х2 + 3,008*(у1 – 1,9х2)/0,696
= 2,559х2 + 4,321у1 – 8,211х2 = 4,321у1
-5,652х2.
Таким образом, b21 =
4,321; a22 = -5,652.
Свободные члены структурной формы находим из
уравнений:
А01 = у1, ср – b12y2, ср – а11х1, ср = 25,967
- 0,743´47,55 – 1,538´5,833 = -0,376;
А02 = у2, ср – b21у1,
ср – а22х2, ср = 47,55 – 4,321´25,967 – 5,652´11,333 = -0,594.
Окончательный вид структурной модели:
у1 = а01 + b12y2 + a11x1 + e1 = -0,376
+ 0,743у2 – 1,538х1 + e1;
y2 = a02 + b21y1 + a22x2 +e2 = -0,594
+ 4,321у1 – 5,652а22 +e2.