Задача 2
Имеются следующие данные по предприятиям отрасли:
|
Предприятие
|
Среднегодовая стоимость основных производственных фондов
млн. руб.
|
Объем произведенной продукции млн. руб.
|
|
1-е
|
3,5
|
2,5
|
|
2-е
|
1,0
|
1,6
|
|
3-е
|
4,0
|
2,8
|
|
4-е
|
4,9
|
4,4
|
|
5-е
|
7,0
|
10,9
|
|
6-е
|
2,3
|
2,8
|
|
7-е
|
6,6
|
10,2
|
|
8-е
|
2,0
|
2,5
|
|
9-е
|
4,7
|
3,5
|
|
10-е
|
5,6
|
8,9
|
|
11-е
|
4,2
|
3,2
|
|
12-е
|
3,0
|
3,2
|
|
13-е
|
6,1
|
9,6
|
|
14-е
|
2,0
|
3,5
|
|
15-е
|
3,9
|
4,2
|
|
16-е
|
3,8
|
4,4
|
|
17-е
|
3,3
|
4,3
|
|
18-е
|
3,0
|
2,4
|
|
19-е
|
3,1
|
3,2
|
|
20-е
|
4,5
|
7,9
|
Для получения зависимости между стоимостью основных производственных
фондов и объемов продукции произведите группировку предприятий по стоимости
основных производственных фондов, образовав четыре группы с равными
интервалами. По каждой группе и в целом по совокупности посчитайте:
число предприятий;
стоимость основных производственных фондов – всего и в
среднем на одно предприятие;
стоимость продукции – всего и в среднем на одно предприятие;
фондоотдачу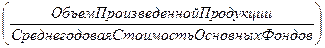 
Результаты представьте в разработочной и групповой таблицах.
Дайте анализ показателей таблицы и сделайте краткие выводы.
Решение
Минимальное значение: 1,0
Максимальное значение: 7,0
Размах: 7 – 1 = 6
Размах одной группы: 6 / 4 = 1,5
|
Группа
|
Предприятие
|
Среднегодовая стоимость основных производственных фондов
млн. руб.
|
Объем произведенной продукции млн. руб.
|
|
1 – 2,5
|
2
|
1,0
|
1,6
|
|
6
|
2,3
|
2,8
|
|
8
|
2,0
|
2,5
|
|
14
|
2,0
|
3,5
|
|
Итого первая группа (среднее)
|
4 предприятия
|
1,825
|
2,6
|
|
2,5 – 4,0
|
1
|
3,5
|
2,5
|
|
3
|
4,0
|
2,8
|
|
12
|
3,0
|
3,2
|
|
15
|
3,9
|
4,2
|
|
16
|
3,8
|
4,4
|
|
17
|
3,3
|
4,3
|
|
18
|
3,0
|
2,4
|
|
19
|
3,1
|
3,2
|
|
Итого вторая группа (среднее)
|
8 предприятий
|
3,45
|
3,375
|
|
4,0 – 5,5
|
4
|
4,9
|
4,4
|
|
9
|
4,7
|
3,5
|
|
11
|
4,2
|
3,2
|
|
20
|
4,5
|
7,9
|
|
Итого третья группа (среднее)
|
4 предприятия
|
4,575
|
4,75
|
|
5,5 – 7,0
|
5
|
7,0
|
10,9
|
|
7
|
6,6
|
10,2
|
|
10
|
5,6
|
8,9
|
|
13
|
6,1
|
9,6
|
|
Итого 4-ая группа (среднее)
|
4 предприятия
|
6,325
|
9,9
|
По каждой группе и в целом по совокупности подсчитаем:
1. Число предприятий
Группа 1 – 2,5:
4
Группа 2,5 –
4,0: 8
Группа 4,0 –
5,5: 4
Группа 5,5 –
7,0: 4
В целом 20
предприятий
2. Стоимость основных производственных фондов – всего и в среднем
на одно предприятие
|
Группа
|
Предприятие
|
Среднегодовая стоимость основных производственных фондов
млн. руб.
|
|
1 – 2,5
|
2
|
1,0
|
|
6
|
2,3
|
|
8
|
2,0
|
|
14
|
2,0
|
|
Всего первая группа
|
4 предприятия
|
7,3
|
|
В среднем по первой группе
|
|
1,825
|
|
2,5 – 4,0
|
1
|
3,5
|
|
3
|
4,0
|
|
12
|
3,0
|
|
15
|
3,9
|
|
16
|
3,8
|
|
17
|
3,3
|
|
18
|
3,0
|
|
19
|
3,1
|
|
Итого вторая группа
|
8 предприятий
|
27,5
|
|
В среднем по второй группе
|
|
3,4375
|
|
4,0 – 5,5
|
4
|
4,9
|
|
9
|
4,7
|
|
11
|
4,2
|
|
20
|
4,5
|
|
Итого третья группа
|
4 предприятия
|
18,3
|
|
В среднем по 3-ей группе
|
|
4,575
|
|
5,5 – 7,0
|
5
|
7,0
|
|
7
|
6,6
|
|
10
|
5,6
|
|
13
|
6,1
|
|
Итого 4-ая группа
|
4 предприятия
|
25,3
|
|
В среднем по 4-ой группе
|
|
6,325
|
|
Итого по всем группам
|
|
78,5
|
|
В среднем по всем группам
|
|
3,925
|
3. Стоимость продукции – всего и в среднем на одно
предприятие:
Общая
стоимость продукции
2,5 + 1,6 +
2,8 + 4,4 + 10,9 + 2,8 + 10,2 + 2,5 + 3,5 + 8,9 + 3,2 + 3,2 +
+9,6 + 3,5 + 4,2 + 4,4 + 4,3 + 2,4 + 3,2 + 7,9 = 96
Средняя стоимость продукции на одно предприятие
96 / 20 = 4,8
4. Фондоотдача
Фондоотдача =
объем произведенной продукции /
среднегодовая
стоимость основных фондов
Среднегодовая
стоимость основных фондов:
3,5
+ 1,0 + 4,0 + 4,9 + 7,0 + 2,3 + 6,6 + 2,0 + 4,7 + 5,6 + 4,2 +
+
3,0 + 6,1 + 2,0 + 3,9 + 3,8 +3,3 + 3,0 + 3,1 + 4,5 = 78,5
Фондоотдача
= 96 / 78,5 ≈ 1,223
Вывод: Большее число предприятия (8) попадает во вторую
группу с интервалом 2,5 – 4,0 млн. руб. основных производственных фондов.
Задача 13
Производство однородной продукции предприятиями объединения
составила:
|
Предприятие
|
Фактически произведено продукции млн.руб.
|
Выполнение плана, %
|
Удельный вес продукции первого сорта, %
|
|
1-е
|
41,2
|
103
|
85
|
|
2-е
|
20,9
|
95
|
80
|
|
3-е
|
32,1
|
107
|
90
|
Вычислить:
1) процент выполнения плана выпуска продукции в среднем по
объединению;
2) средний процент выпуска продукции первого сорта по
объединению.
Дать обоснование применения формул средних для расчета
показателей. Сделать выводы.
Решение
1) Для вычисления среднего процента выполнения плана по
объединению, нужно вычислить средний процент выполнения плана по всем 3
предприятиям:
(103 + 95 +
107) / 3 = 305 /3 ≈ 101,67%
2) Для вычисления среднего процента выпуска продукции
первого сорта по объединению, нужно найти среднее значение удельного веса
продукции 1-го сорта:
(85 + 80 + 90)
/ 3 = 255 / 3 = 85%
Выводы. Второе
предприятие выполнило план ниже среднего показателя по объединению, а первое и
третье предприятия выполнили план выше среднего уровня.
Средний процент продукции первого сорта по всем предприятия
составил 85%. Первое предприятие выполнило средний уровень продукции первого
сорта, у второго предприятия – меньше среднего, у третьего предприятия – выше
среднего.
Задача 23
Данные об объеме розничного товарооборота на душу населения
Новосибирской области:
|
Год
|
Продажа на душу населения, руб
|
|
1995
|
2974
|
|
1996
|
4496
|
|
1997
|
6902
|
|
1998
|
7932
|
|
1999
|
11031
|
Определить:
1) вид динамического ряда;
2) средний уровень динамического ряда;
3) абсолютные приросты, темпы роста и прироста, цепные и
базисные, абсолютно содержание 1% прироста;
4) средний абсолютный прирост, средний темп роста и прироста
уровней динамического ряда.
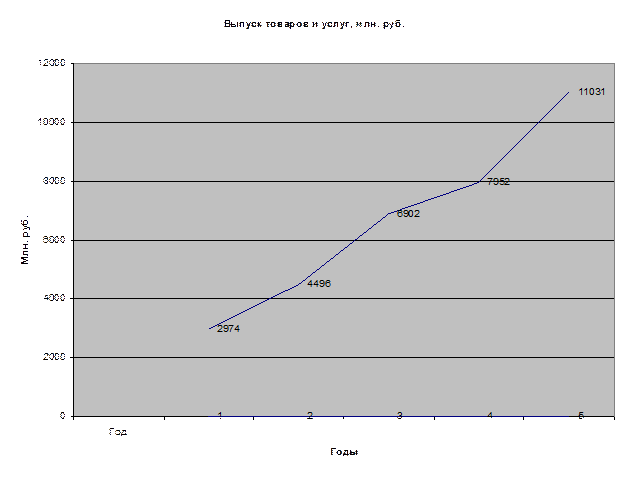
Результаты расчетов представьте в таблице. Изобразите
динамический ряд на графике. Сделайте выводы.
Решение.
1. Вид динамического ряда: интервальный
2. Средний уровень ряда:
(2974 + 4496 +
6902 +7952 + 11031)/5 = 6667 млн. руб.
3. Рассчитаем абсолютные приросты, темпы роста и прироста
(цепные и базисные), абсолютное содержание 1% прироста:
|
Год
|
Выпуск товаров и услуг млн. руб.
|
Абсолютный прирост
|
Темп роста
|
Темп прироста
|
Значение 1% прироста
|
|
Цепной
|
Базисный
|
Цепной
|
Базисный
|
Цепной
|
Базисный
|
|
1
|
2974
|
Х
|
Х
|
Х
|
Х
|
Х
|
Х
|
Х
|
|
2
|
4496
|
1522
|
1522
|
1,51
|
1,51
|
0,51
|
0,51
|
29,74
|
|
3
|
6902
|
2406
|
3928
|
1,54
|
2,32
|
0,54
|
1,32
|
44,96
|
|
4
|
7952
|
1050
|
4978
|
1,15
|
2,67
|
0,15
|
1,67
|
69,02
|
|
5
|
11031
|
3079
|
8057
|
1,39
|
3,71
|
0,39
|
2,71
|
79,52
|
|
Итого
|
33355
|
8057
|
18485
|
Х
|
Х
|
Х
|
Х
|
Х
|
4. Средний абсолютный прирост, средний темп роста и прироста
уровней динамического ряда
Средний
абсолютный прирост: 8057 / 4 = 2014,25
Средний темп
роста: (1,51 + 1,54 + 1,15 + 1,39) / 4 = 1,3975
Средний темп
прироста: 1,3975 - 1 = 0,3975
Задача 44
Производство продукции и ее себестоимости на предприятии за
два периода составили:
|
Наименование продукции
|
Себестоимость единицы продукции, руб
|
Произведено продукции, тыс. шт.
|
|
базисный период
|
отчетный период
|
базисный период
|
отчетный период
|
|
А
|
82
|
105
|
121
|
97
|
|
Б
|
110
|
97
|
86
|
132
|
|
В
|
173
|
158
|
73
|
72
|
Определить:
1) индивидуальные индексы себестоимости и количества
произведенной продукции;
2) общий индекс затрат на производство;
3) общий индекс себестоимости;
4) общий индекс физического объема произведенной продукции;
5) абсолютный размер изменения затрат производства – всего,
в том числе за счет изменения себестоимости продукции и физического объема
продукции
Показать взаимосвязь индексов. Сделать выводы.
Решение.
1. Взаимосвязь индексов себестоимости и количества
произведенной продукции
себестоимость продукции «А»: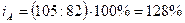 
, т.е. себестоимость продукции «А» увеличилась в отчетном
периоде по сравнения с базисным на 28% или на 105-82=23 рубля;
количество продукции «А»: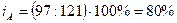 
, т.е. количество выпускаемой продукции «А» уменьшилось в
отчетном периоде по сравнению с базисным на 20% или на 121-97=24 штуки;
себестоимость продукции «Б»: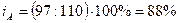 
, т.е. себестоимость продукции «Б» уменьшилась в отчетном
периоде по сравнению с базисным на 12% или 110-97=13 рублей;
количество продукции «Б»: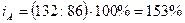 
, т.е. количество выпускаемой продукции «Б» увеличилось в
отчетном периоде по сравнению с базисным на 53% или 132-86=46 штук;
себестоимость продукции «В»: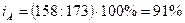 
, т.е. себестоимость продукции «В» уменьшилась в отчетном
периоде по сравнению с базисным на 9% или 173 – 158 = 15 рублей;
количество продукции «В»: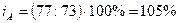 
, т.е. количество выпускаемой продукции «В» увеличилось в
отчетном периоде по сравнению с базисным на 5% или 77-73=4 штуки.
2. Общий индекс затрат на производство
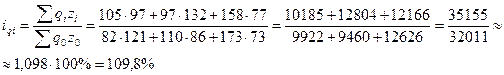
3. Общий индекс себестоимости
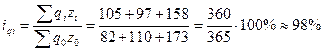Себестоимость всех
видов продукции в отчетном периоде по сравнению с базисным уменьшилось на 2%
(100-98) или на 5 тысяч рублей (365 - 360).
4. Общий индекс физического объема произведенной продукции
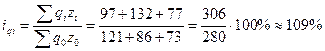Объем всех видов
продукции в отчетном периоде по сравнении с базисным возрос на 9% или на 26
тыс. штук.
5. Абсолютный размер изменения затрат производства:
всего: (105*97 + 97*132 + 158*77)
– (82*121 + 110*86 + 173*73) = 3144
за счет изменения
себестоимости: (105+97+158)/(82+110+173)=0,9896
за счет изменения объема:
(97+132+77)/(105+97+158)=0,85
ВЫВОДЫ: Наибольшую себестоимость
имеет продукция типа «А», а наименьшую – типа «Б». Наибольшее количество
продукции типа «Б», а наименьшее – типа «В».
Задача 66
Данные о численности работников университета, начавшего свою
работу 22 января (чел):
|
Число месяца
|
Списочная численность
|
Явочная численность
|
|
А
|
1
|
2
|
|
Январь
|
|
|
|
22
|
65
|
65
|
|
23
|
65
|
63
|
|
24
|
67
|
63
|
|
25
|
68
|
65
|
|
26
|
68
|
66
|
|
27
|
68
|
67
|
|
29
|
70
|
68
|
|
30
|
69
|
69
|
|
31
|
70
|
66
|
|
Март
|
|
|
|
1
|
72
|
70
|
|
2
|
72
|
70
|
|
3
|
71
|
68
|
|
5
|
71
|
67
|
|
6
|
70
|
67
|
|
7
|
69
|
68
|
|
9
|
69
|
65
|
|
10
|
70
|
68
|
|
12
|
70
|
69
|
|
13
|
73
|
70
|
|
14
|
73
|
71
|
|
15
|
73
|
71
|
|
16
|
73
|
73
|
|
17
|
72
|
70
|
|
19
|
72
|
72
|
|
20
|
72
|
71
|
|
21
|
73
|
70
|
|
22
|
73
|
72
|
|
23
|
72
|
71
|
|
24
|
72
|
69
|
|
26
|
71
|
70
|
|
27
|
71
|
69
|
|
28
|
71
|
68
|
|
29
|
71
|
70
|
|
30
|
69
|
66
|
|
31
|
69
|
67
|
Рассчитать:
1) среднеявочную численность работников за январь и март
2) среднесписочную численность работников за январь, март и
за первый квартал
Решение
1) Среднеявочную численность работников за январь и март
найдем как среднее арифметическое.
(65 + 63 + 63
+ 65 + 66 + 67 + 68 + 69 + 66 +
+ 70 + 70 + 68 + 67 + 67 + 68 + 65 + 68 + 69 + 70 + 71 + 71
+ 73 + 70 + 72 +
+ 71 + 70 + 72 + 71 + 69 + 70 + 69 + 68 + 70 + 66 + 67) / 35
= 2394 / 35 =
= 68,4 ≈ 68
2) Среднесписочная численность за январь:
(65 + 65 + 67
+ 68 + 68 + 68 + 70 + 69 + 70) / 9 = 67,77777778
≈ 68
Среднесписочная
численность за март:
(72 + 72 + 71
+71 + 70 + 69 + 69 + 70 + 70 + 73 + 73 + 73 + 73 + 72 + 72 +
+ 72 + 73 + 73 + 72 + 72 + 71 + 71 + 71 + 71 + 69 + 69) / 16
=
= 71,30769231 ≈ 71
Среднесписочная
численность за 1 квартал:
(68 + 64 + 71) / 3 = 203 / 3 ≈
68
Задача 76
Численность работников торговли сократилась на 5%, а средняя
выработка возросла на 30%.
Определить, как изменился объем оборота. Привести формулы
используемых индексов. Показать их взаимосвязь.
Решение
Пусть х – число работников, y – средняя выработка, xy – объем
выработки
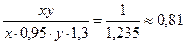
Вывод: объем оборота сократился на 100 – 81 = 19%
Задача 98
Имеются следующие данные об обороте розничной торговли и
численности населения района, обслуживаемого потребительской кооперацией, за
два года:
|
Показатели
|
Базисный год
|
Отчетный год
|
|
Оборот, млн. руб.
|
226,8
|
266,4
|
|
Среднегодовая численность обслуживаемого населения, тыс.
чел.
|
36
|
37
|
Определить:
1) оборот на душу населения;
2) общую сумму прироста оборота в отчетном году по сравнению
с базисным – всего, в том числе за счет изменения продажи на душу населения и
численности населения;
3) долю прироста оборота за счет каждого фактора.
Сделать выводы.
Решение.
1) оборот на душу населения
в базисном
году: 226800000 / 36000 = 6300 (руб / чел)
в отчетном
году: 266400000 / 37000 = 7200 (руб / чел)
средний
оборот: (6300 + 7200) / 2 = 6750 (руб / чел)
2) сумма прироста оборота в отчетном году по сравнению с
базисным
всего:
266400000 – 226800000 = 39600000 (руб)
за счет
изменения продажи на душу:
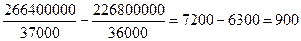
за счет
изменения численности населений:
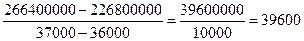
3) доля прироста оборота за счет каждого фактора
за счет изменения продажи на
душу населения: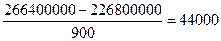 
за счет изменения численности
населения
Выводы: Оборот на
душу населения возрос, большей частью за счет увеличения продажи на душу
населения.
Задача 116
Сведения об обороте, издержках обращения в действующих ценах
и изменение цен на товары, тарифов и ставок на услуги торговой организации:
|
Показатели
|
Сумма, тыс.руб.
|
Индексы цен,
тарифов и ставок
|
|
базисный период
|
отчетный период
|
|
Оборот
|
18408
|
22090
|
1,15
|
|
Издержки обращения
|
4050
|
5081
|
1,2
|
Рассчитать относительный уровень издержек обращения в
отчетном и базисном периодах в действующих и сопоставимых ценах, тарифах и
ставках. Разложить абсолютное изменение суммы издержек по факторам: за счет
динамики физического объема оборота, уровня издержек и цен, тарифов, ставок.
Решение.
1) относительный уровень издержек в действующих ценах в
отчетном периоде:
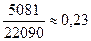
2) относительный уровень издержек в действующих ценах в
базисном периоде:
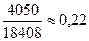
3) относительный уровень издержек в сопоставимых ценах в
отчетном периоде:
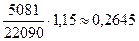
4) относительный уровень издержек в сопоставимых ценах в
базисном периоде:
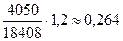
5) абсолютное изменение суммы издержек
5081-4050=1031
6) изменение суммы издержек за счет динамики физического
объема оборота:
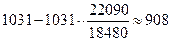
7) изменение суммы издержек за счет динамики уровня издержек
и цен, тарифов, ставок:
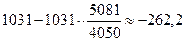
Выводы: за счет
динамики физического объема издержки возросли, а за счет динамики цен, тарифов
и ставок, издержки уменьшились