Содержание

Задача 4. 3

Задача 14. 4

Задача 24. 4

Задача 34. 5

Задача 44. 5

Список литературы.. 7

 

Задача 4

          Рассчитайте, какой будет сумма на счёте, если вклад 10000 рублей положен на 2,5 года под 4% годовых, проценты сложные и начисляются:

a)     Раз в год;

b)    Раз в полугодие;

c)     Ежеквартально;

d)    Ежемесячно;

e)     Ежедневно;

f)      Непрерывно.

Решение:

          Расчет проводится по формуле сложных процентов, которая имеет следующий  общий вид:

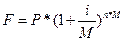          , где

          F – искомая сумма;

          Р – начальная сумма, на которую начисляются проценты;

          i – процентная ставка;

          М – количество начислений в год;

          n – срок вклада;

          Подставляя в эту формулу числовые значения, получим следующие результаты:

a)     ;

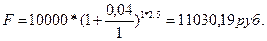b)    ;

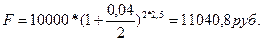c)     ;

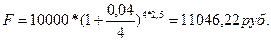d)    ;

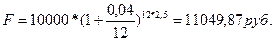e)     ;

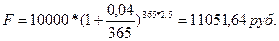f)      Для непрерывного начисления процентов существует упрощённая формула: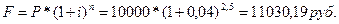

Задача 14

          Два платежа в 3000 и 4000 рублей со сроками выплат 1 и 2 года соответственно заменяются одним платежом через 2,5 года. Найти величину платежа. Используется сложная процентная ставка 12% годовых, начисление ежеквартальное.

Решение:

          При указанных условиях сумма выплат должна составить:

          F1 + F2 = 8443,6 руб.;

          ;

          ;

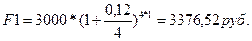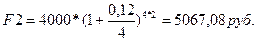          Для нахождения начальной суммы платежа при сроке выплаты через 2,5 года используем формулу дисконтирования:

          ;

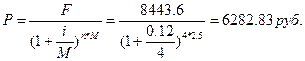Ответ: величина платежа 6282,83 руб.

Задача 24

          Рассчитайте, какая сумма будет через 4 года на счёте, если в конце каждого месяца вносится по 1000 рублей. Проценты сложные, начисление ежемесячное, годовая ставка 4%.

Решение:

          Для решения этой задачи используем формулу будущей стоимости обыкновенного аннуитета: 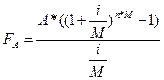, где А – сумма платежа.

          ;

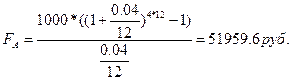Ответ: через 4 года на счёте будет 51959,6 рублей.

Задача 34

          Заменить ренту, полученную в задаче 24 на двухлетнюю годовую ренту постнумерандо при тех же банковских условиях. Определить величину годового взноса.

Решение:

          Для получения на счёте через 2 года 51959,6 рублей годовой платёж должен составить:

           

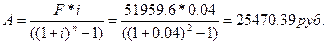
Ответ: годовой взнос составит 25470,39 рублей.

Задача 44

          Заём в 200000 рублей выдан на 4 года, под 8% годовых. Начисление ежегодное. Составить семь планов погашения займа, найти современную величину каждого потока выплат. Заполнить таблицу:

Решение:

Выплаты	1 год	2 год	3 год	4 год	Современная величина
Погашение одним платежом в конце периода				272097,79	272097,79
Погашение основного долга одним платежом	16000	16000	16000	216000	264000
Погашение основного долга равными годовыми выплатами	66000	62000	58000	54000	240000
Погашение займа равными годовыми выплатами	60384,16	60384,16	60384,16	60384,16	241536,64
Создание погасительного фонда (ставка 30% в год)	43975,95	43975,95	43975,95	43975,95
Погашение потребительского кредита (выплата раз в год в начале года)	66000	66000	66000	66000	264000
Погашение ипотечной ссуды	48000	48000	48000	48000

Список литературы

1.     Башарин Г.П. Начала финансовой математики. – М.: «Инфра-М», 1997.

2.     Ковалёв В.В. Задачи по финансовому анализу. – М.: «Финансы и статистика», 1997.

3.     Ковалёв В.В. Курс финансовых вычислений. – М.: «Финансы и статистика», 1999.

4.     Кочович Е. Финансовая математика. – М.: «Финансы и статистика», 1994.

5.     Малыхин В.И. Финансовая математика. – М.: «Юнити», 1999.