Министерство образования и науки Российской Федерации
Федеральное агентство по образованию ГОУ ВПО
Всероссийский заочный финансово-экономический институт
Кафедра экономико-математических методов и моделей
ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ
по дисциплине
«Экономико-математические методы и прикладные модели»
Вариант № 25
Преподаватель: Прокофьев Олег Владимирович
Работа выполнена: студент Семёнова Тамара Викторовна
ФК, 3
курс, личное дело № 06ффб02825, группа №4
Пенза – 2008
Задача 1
(вариант 15)
Необходимо решить
транспортную задачу – минимизировать расходы на доставку продукции заказчикам
со складов фирмы, учитывая следующие затраты на доставку одной единицы
продукции, объём заказа и количество продукции, хранящейся на каждом складе.
Таблица тарифов на
перевозку продукции и объёмов запасов на складе и заказов:
|
Магазин
|
"Свадебный
салон"
|
ГУМ
|
ЦУМ
|
"Салон для
новобрачных"
|
Запасы на
складе (ед. продукции)
|
|
Склад
|
|
Динамо
|
0
|
1
|
0,5
|
2
|
25
|
|
Сокольники
|
2
|
3
|
2
|
1
|
15
|
|
Кусково
|
3
|
2
|
1
|
0,5
|
10
|
|
Объём заказа
(ед. продукции)
|
15
|
20
|
15
|
10
|
|
1. Постановка задачи
Таблица 1.
Исходные данные
|
Склады
|
Клиенты
|
Ресурсы
|
|
К1
|
К2
|
К3
|
К4
|
|
С1
|
0
|
1
|
0,5
|
2
|
25
|
|
С2
|
2
|
3
|
2
|
1
|
15
|
|
С3
|
3
|
2
|
1
|
0,5
|
10
|
|
Заказы
|
15
|
20
|
15
|
10
|
|
Имеется 4 заказа от 4
потребителей. Заказы в сумме больше запаса на складах С1,…,С3. Найти план
перевозок, минимизирующий транспортные издержки.
2. Экономико-математическая
модель задачи
В данном случае суммы
заказов потребителей и запасы на складах поставщиков не совпадают, т. е. имеем
дело с открытой моделью транспортной задачи.
Транспортная задача
относится к двухиндексным ЗЛП, так как в результате её решения необходимо найти
матрицу Х с компонентами Xij. Обозначим через Xij количество единиц груза (продукции
фирмы), запланированных к перевозке от поставщика к заказчику. Так как от
поставщика I к заказчику j запланировано перевезти Xij единиц груза, то стоимость перевозки составит CijXij. Стоимость всего плана выразится
двойной суммой: 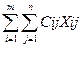 . Систему ограничений получаем из следующих условий задачи:
а) все грузы должны быть перевезены, т. е.
. Систему ограничений получаем из следующих условий задачи:
а) все грузы должны быть перевезены, т. е. 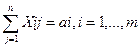
б) все потребности должны
быть удовлетворены, т. е. 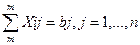
В нашем случае суммарные
потребности превышают суммарные запасы: 
Запишем целевую функцию:
F=x11∙0+x12∙1+x13∙0,5+x14∙2+x21∙2+x22∙3+x23∙2+x24∙1+x31∙3+x32∙2+
+x33∙1+x34∙0,5+x41∙0+x42∙0+x43∙0+x44∙0 → min
Ограничения:
Xij ≥0
1) по строкам
x11+x12+x13+x14=25
x21+x22+x23+x24=15
x31+x32+x33+x34=10
x41+x42+x43+x44=10
2) по столбцам
y11+y12+y13+y14=15
y21+y22+y23+y24=20
y31+y32+y33+y34=15
y41+y42+y43+y44=10
Добавим строку фиктивного
поставщика, тогда таблица 2 примет вид:
Таблица 2.
Добавление фиктивного поставщика
|
Склады
|
Клиенты
|
Ресурсы
|
|
К1
|
К2
|
К3
|
К4
|
|
С1
|
0
|
1
|
0,5
|
2
|
25
|
|
С2
|
2
|
3
|
2
|
1
|
15
|
|
С3
|
3
|
2
|
1
|
0,5
|
10
|
|
|
0
|
0
|
0
|
0
|
10
|
|
Заказы
|
15
|
20
|
15
|
10
|
|
Составим матрицу с
исходными данными задачи (рис. 1).
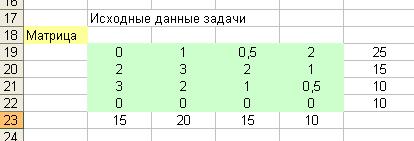
Рис. 1.
Матрица с исходными данными задачи
Создадим матрицу
перевозок. Для этого необходимо выполнить резервирование изменяемых ячеек: в
блок ячеек B27:E30 вводится «1». Таким образом, резервируется место, где после решения задачи
будет находиться распределение поставок, обеспечивающее минимальные затраты на
перевозку груза (рис. 2).
Введём граничные условия
– условия реализации поставок. Введение условия реализации продукции
поставщиков, т. е. 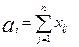 ,где
,где 
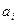 - запас на складе i-ого поставщика,
- запас на складе i-ого поставщика, 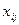 - объём поставки груза
от i-ого поставщика
к j-му потребителю,
n – количество
потребителей.
- объём поставки груза
от i-ого поставщика
к j-му потребителю,
n – количество
потребителей.
Для этого необходимо
выполнить следующие операции: курсор в ячейку F27, щёлкнуть значок «∑»,
выделить необходимые для суммирования ячейки B27:E27, нажать ENTER. После протащить (копировать)
формулу в ячейки F28:F30.
Введение условия
удовлетворения запросов потребителей, т. е. 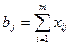 , где b – объём заказа j-ого потребителя, m – количество поставщиков.
, где b – объём заказа j-ого потребителя, m – количество поставщиков.
Для этого необходимо:
поставить курсор в B31, щёлкнуть знак «∑», при этом автоматически выделяется весь
столбец B27:B30, далее ENTER, после протащить (копировать) формулу в ячейки C31:E31 (рис. 2).
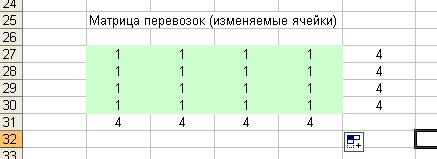
Рис. 2.
Матрица перевозок
3. Назначение целевой
функции.
Для вычисления значения
целевой функции, соответствующей минимальным суммарным затратам на доставку
груза, необходимо зарезервировать ячейку и ввести формулу для её вычисления: 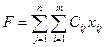 , где
, где  - стоимость доставки
единицы груза от i-ого поставщика к j-ому потребителю,
- стоимость доставки
единицы груза от i-ого поставщика к j-ому потребителю, 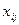 - объём поставки груза
от i-ого поставщика
к j-му потребителю.
- объём поставки груза
от i-ого поставщика
к j-му потребителю.
Для этого: курсор в
ячейку F24. В данной ячейке будет помещаться значение целевой функции после
решения задачи, щёлкнуть «Мастер функций», в окне «Категория» выбрать
«Математические», в оке «Функция» выбрать СУММПРОИЗВ, в окне СУММПРОИЗВ указать
адреса массивов. В поле «Массив 1» указать адреса ячеек B19:E22, в поле «Массив 2» - B27:E30.
4. Ввод зависимостей из
математических моделей.
Осуществим ввод
зависимостей из математических моделей. Для этого нужно: щёлкнуть «Сервис»,
«Поиск решения», «Установить целевую (ячейку)», ввести адрес $F$24. Установить направление целевой
функции, равное «минимальному значению», щёлкнуть в поле «изменяя ячейки»,
ввести адреса $B$27:$E$30.
5. Ввод ограничений.
Введём ограничения. В
матрицу перевозок, содержащую исходные данные по задаче, необходимо ввести
условие реализации всех запасов на складах поставщика. Для этого введём $F$27:$F$30=$F$19:$F$22. Далее вводим ограничение,
которое реализует условие удовлетворения заказов всех потребителей. Для этого $B$21:$E$31=$B$23:$E$23. Далее введём ограничение, говорящее,
что все Х должны быть не меньше 0. (рис. 3)
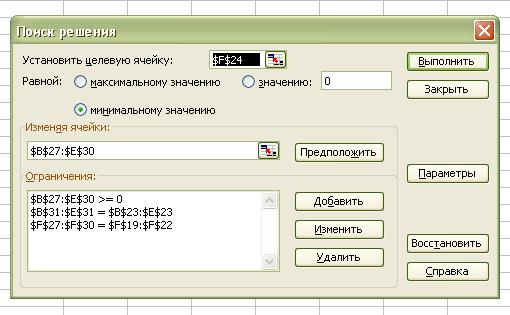
Рис. 3. Ввод
зависимостей из математической модели
Далее необходимо
установить ограничения на решение задачи. Для этого нужно щёлкнуть «Параметры»,
установить «Линейная модель», установить «Неотрицательные значения», так как
объёмы поставок груза отрицательной величиной быть не могут (рис. 4). После
этого осуществим выход в поле «Поиск решений». Далее «Выполнить». После
выполнения вышеуказанных действий на экран выводится окно «Результаты поиска
решения».
Теперь в матрице
перевозок содержатся оптимальные объёмы поставок грузов от поставщика к
потребителям, дающие минимум затрат на доставку. Значение целевой функции
содержится в ячейке F24 и для конкретной задачи равно 40 (рис. 5).
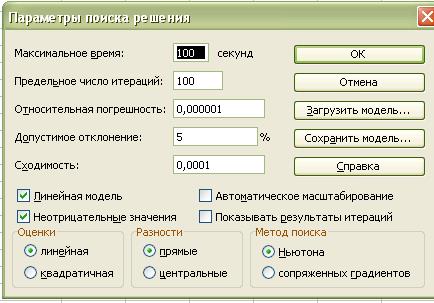
Рис. 4.
Установление параметров задачи
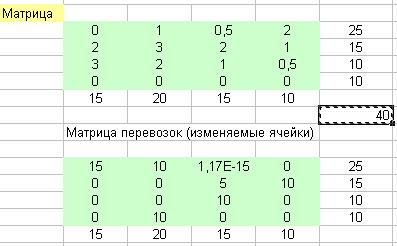
Рис. 5. Задача решена
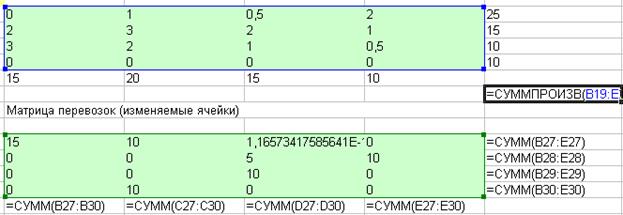
Рис. 6. Задача решена, формульный вид
6. Рекомендации лицу,
ответственному за принятие решений.
Из вышеизложенного можно
сделать следующий вывод: минимум затрат на доставку продукции, равный 40
условных денежных единиц, будет обеспечен при следующем плане поставок: от
первого поставщика первому потребителю в объёме 15 ед.; от первого поставщика
второму потребителю в размере 10 ед.; от второго поставщика третьему потребителю
в размере 5 ед.; от второго поставщика четвёртому потребителю в размере 10 ед.;
от четвёртого поставщика второму потребителю в размере 10 ед. продукции.
При данной схеме поставок
объём продукции со складов поставщика будет реализован, и спросы всех
покупателей будут удовлетворены.
Задача 2
(вариант 17)
Хлебозавод имеет
возможность производить различные хлебобулочные изделия. Нормы затрат различных
типов сырья, их наличие и стоимость единицы продукции каждого вида приведены
ниже.
|
Сырьё
|
Нормы затрат
|
Наличие, кг
|
|
Хлеб
"Бородинский"
|
Хлеб
"Жито"
|
Батон
"Чайный"
|
Батон
"Городской"
|
|
Мука пшеничная
|
0,2
|
0,15
|
0,4
|
0,35
|
500
|
|
Мука ржаная
|
0,25
|
0,3
|
0
|
0
|
250
|
|
Яйцо
|
0,02
|
0,025
|
0,04
|
0,035
|
100
|
|
Масло
|
0,01
|
0,03
|
0,1
|
0,15
|
200
|
|
Дрожжи
|
0,005
|
0,85
|
0,7
|
0,6
|
15
|
|
Вес изделия
|
0,65
|
0,85
|
0,7
|
0,6
|
|
|
Стоимость
одного изделия
|
7
|
8
|
9
|
8
|
|
После проведения
маркетинговых исследований установлено, что ежедневный спрос на «Бородинский»
хлеб колеблется в пределах от 150 до 300 кг; спрос на хлеб «Жито» меняется
соответственно от 300 до 450
кг; на батон «Чайный» - от 200 до 300 кг; на батон «Городской»
– от 200 до 400 кг.
Определить оптимальный ежедневный объём выпускаемой хлебобулочной продукции,
обеспечивающий её максимальную стоимость.
1. Постановка задачи.
Для производства продукции
типа П1, П2, П3, П4, предприятие использует 5 видов сырья: С1, С2, С3, С4, С5.
Данные об условиях производства приведены в таблице 1. Составить план
производства по критерию «максимум прибыли».
Таблица 1. Исходные данные
|
Сырье
|
Расход сырья на
ед. продукции
|
Наличие, кг
|
|
П1
|
П2
|
П3
|
П4
|
|
С1
|
0,2
|
0,15
|
0,4
|
0,35
|
500
|
|
С2
|
0,25
|
0,3
|
0
|
0
|
250
|
|
С3
|
0,02
|
0,025
|
0,04
|
0,035
|
100
|
|
С4
|
0,01
|
0,03
|
0,1
|
0,15
|
200
|
|
С5
|
0,005
|
0,85
|
0,7
|
0,6
|
15
|
|
вес изделия
|
0,65
|
0,85
|
0,7
|
0,6
|
|
|
стоимость
одного изделия
|
7
|
8
|
9
|
8
|
|
2.
Экономико-математическая модель задачи
Обозначим через х1, х2,
х3, х4 продукцию каждого типа. Целевая функция – это выражение, которое
необходимо максимизировать. F=7x1+8x2+9x3+8x4.
Ограничения по ресурсам:
0,2х1+0,15х2+0,4х3+0,35х4≤500
– ограничение по ресурсу С1
0,25x1+0,3x2≤250 – ограничение по ресурсу
С2
0,02х1+0,025х2+0,04х3+0,035х4≤100
– ограничение по ресурсу С3
0,01х1+0,03х2+0,1х3+0,15х4≤200
– ограничение по ресурсу С4
0,005х1+0,005х2+0,01х3+0,01х4≤15
– ограничение по ресурсу С5
150≤0,65х1≤300
300≤0,85х2≤450
200≤0,7х3≤300
200≤0,6х4≤400
х1, х2, х3, х4 – целые
числа
х1, х2, х3, х4 ≥ 0
В данной задаче
оптимизационные значения вектора Х=(х1,х2,х3,х4) будут помещены в ячейках В15:Е15,
оптимальное значение целевой функции будет находиться в ячейке F16.
Вводим зависимость для целевой
функции. Поместим курсор в ячейку F16, из меню мастер функции выбираем
функцию СУММПРОИЗВ. Появляется диалоговое окно, в строке «Массив 1» вводим В$15:Е$15,
в строке «Массив 2» - В16:Е16. Массив будет использоваться при вводе
зависимостей для ограничений, поэтому на этот массив нужно делать абсолютную
ссылку (рис. 2).
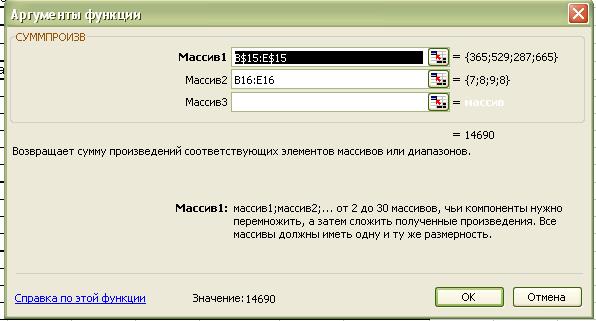
Рис. 2. Ввод
данных для функции СУММПРОИЗВ
Вводим зависимости для
ограничений. Копируем из ячейки F16 формулу в ячейку F19, затем автозаполнением заполняем
ячейки F20:F23.
Затем запускаем команду
Поиск решения. Устанавливаем целевую ячейку (F16), вводим тип целевой функции в
зависимости от условия задачи. Для этого отметим, чему равна целевая функция. В
данной задаче – максимальному значению. Помещаем курсор в троку Изменяя
значения. Вводим адреса искомых переменных В$15:Е$15.
Вводим ограничения. В
строке Ссылка на ячейку вводим адрес $F$19, выбираем знак (в данном случае
≤), в троке Ограничения вводим $Н$19. Остальные ограничения вводим
аналогичным образом (Рис. 3).
Далее вводим параметры
для решения задачи линейного программирования (Рис. 4). Устанавливаем флажки в
окнах Линейная модель (это обеспечит применение симплекс-метода) и
Неотрицательные значения.

Рис. 3. Поиск
решения
Помещаем курсор на кнопку
ОК. Появляется диалоговое окно Поиск решения. Нажимаем Выполнить.
Рис. 4. Ввод
параметров
После нажатия кнопки
появляется диалоговое окно Результаты поиска решения, где указываем тип отчёта:
по результатам, устойчивости, пределам. Получаем исходную таблицу с заполненными
ячейками В15:Е15 для значений х1, х2, х3, х4 и заполненную ячейку F16 с максимальным значением целевой
функции (Рис. 5).
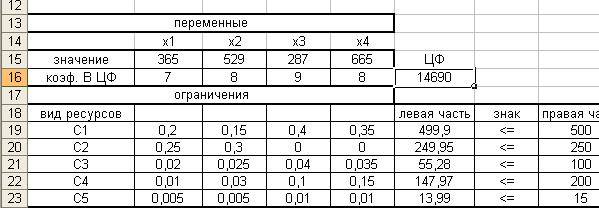
Рис. 5.
Решение найдено
В результате решения
задачи был получен ответ: чтобы обеспечить максимальную прибыль, оптимальный
ежедневный объём выпускаемой продукции должен быть равен для хлеба «Бородинский» 365 ед., для хлеба «Жито»
529 ед., для батона «Чайный» 287 ед., для батона «Городской» 665 ед. Если
производитель будет следовать этому решению, то конечная прибыль составит 14690
условных денежных ед.