Введение

Роль статистики при переходе к рыночным отношениям, как известно, возрастает. Статистика выступает не только как действенный инструмент анализа рыночной экономики, но и как своеобразный арбитр по оценке условий и результатов ее развития, одновременно являясь мощным орудием преобразования рыночных социально – экономических отношений, важным дополнительным фактором оперативного, предприимчивого и эффективного их совершенствования.

Статистические исследования предприятий предполагает проведение статистического наблюдения, организацию сбора статистической информации о предприятиях, ее систематизации и классификации. Это позволяет с помощью статистических методов получить обобщающие характеристики и выявить закономерности, существующие в сфере трудовой деятельности в конкретных условиях места и времени.

Целью данной курсовой работы является анализ деятельности организаций (предприятий) и использование статистических методов в оценке их результативности.

В теоретической части курсовой  работы рассмотрены следующие аспекты:

1) Классификация и группировка как метод обработки и анализа

       первичной   статистической информации.

2) Виды группировок. Статистическая таблица

Расчетная часть курсовой работы  включает решение трех задач:

1) Работа с таблицей «Статистические методы изучения предприятий», определение средних величин и показателей вариации.

2) Вычисление абсолютных и относительных статистических показателей изменения уровней, средних показателей динамики ряда.

3) Определение цепных и базисных индексов.

1. Теоретическая часть

1.1. Классификация и группировка как метод обработки и анализа первичной статистической информации

В практической статистике широко применяется метод классификаций и группировок. Классификация - это систематическое распределение явлений

и объектов по определенным группам, классам, разрядам на основании их сходства и различия. Используют классификации: отраслевую; профессиональную; основных фондов; капитальных вложений.

Для дальнейшей обработки собранных в ходе статистического наблюдения первичных данных широко используют и метод группировки.

Группировка - это распределение множества единиц исследуемой совокупности по группам в соответствии с существенным для данной группы признаком. Метод группировки позволяет обеспечивать первичное обобщение данных, представление их в более упорядоченном виде. Благодаря группировке можно соотнести сводные показатели по совокупности в целом со сводными показателями по группам. Появляется возможность сравнивать, анализировать причины различий между группами, изучать взаимосвязи между признаками.

Группировка позволяет делать вывод о структуре совокупности и о роли отдельных групп этой совокупности. Именно группировка формирует основу для последующей сводки и анализа данных.

 Признаки, по которым проводится группировка, называют группировочными признаками. Группировочный признак иногда называют основанием группировки. Правильный выбор существенного группировочного признака дает возможность сделать научно обоснованные выводы по результатам статистического исследования. Группировочные признаки могут иметь как количественное выражение (объем, доход, курс валюты, возраст и т.д.), так и  качественное (форма собственности предприятия, пол человека, отраслевая принадлежность, семейное положение и т.д.).

Если для построения группировки используется только один признак, то такую группировку называются простой, если группировка проводится по нескольким признакам, ее называют сложной. Сложная группировка бывает или комбинационная, или многомерная.

Комбинационная группировка выполняется последовательно: группы, выделенные по одному признаку, затем выделяются в подгруппы по другому признаку, которые, в свою очередь, могут выделяться по следующему другому признаку. В этом случае число групп будет равно произведению числа выделенных групп на число группировочных признаков. Процедура определения оптимального числа групп основана на применении формулы Стерджесса:

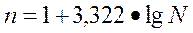
            где n - число групп;

                  N - число единиц совокупности.

Из формулы видно, что выбор числа групп зависит от объема совокупности. Если групп оказывается много, и они включают малое число единиц, то групповые показатели могут стать ненадежными. Поэтому альтернативой комбинационной группировке является многомерная группировка, которая осуществляется по комплексу признаков одновременно.

Определение числа групп тесно связано с понятием  величина интервала: чем больше число групп, тем меньше величина интервала, и наоборот. Интервал - разница между максимальным и минимальным значениями признака в каждой группе. Он определяет количественные границы групп, что для статистической практики имеет большое значение, особенно когда нужно образовать качественно однородные группы.

Каждый интервал имеет нижнюю (наименьшее значение признака) и верхнюю (наибольшее значение признака) границы или одну из них. Поэтому величина интервала есть разность между верхней и нижней границами интервала. Если у интервала указана лишь одна граница (у первого - верхняя, у последнего - нижняя), то речь идет об  открытых интервалах. Если у интервала имеются и нижняя, и верхняя границы, то речь идет о  закрытых интервалах. Закрытые интервалы подразделяются на равные и неравные (прогрессивно возрастающие, прогрессивно убывающие), а также специализированные и произвольные.

Группировку с  равными интервалами строят тогда, когда исследуются количественные различия в величине признака внутри групп одинакового качества, а также если распределение носит более или менее равномерный характер. Если можно заранее установить определенное количество групп, то величину равного интервала можно вычислить по формуле:

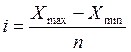
    где i - величина равного интервала;

              x_max , x_min - наибольшее и наименьшее значения признака;

              n - число групп.

1.2. Виды группировок. Статистическая таблица

Виды группировок зависят от целей и задач, которые они выполняют. С помощью метода статистических группировок выделяют качественно однородные совокупности, изучают структуры совокупности и изменения, происходящие в них, а также решают задачи по исследованию существующих связей и зависимостей.

С известной мерой условности для выполнения этих задач группировки соответственно делят на типологические, структурные и аналитические.

Метод типологической группировки заключается в выявлении в качественно разнородной совокупности однородных групп. При этом очень важно правильно отобрать группировочный признак, который поможет идентифицировать выбранный тип. Типологические группировки широко применяются в исследовании социально-экономических явлений. Примерами такого вида группировок могут быть объемы производства продукции по федеральным округам, по формам хозяйствования, социальные группы населения и т.д. В типологических группировках часто используются специализированные интервалы.

Метод структурной группировки есть разделение однородной совокупности на группы по тому или иному варьирующему группировочному признаку. Примерами такого вида группировок могут быть группы населения по полу, возрасту, месту проживания, доходу и т.д., то есть может решаться задача по изучению структурного состава той или иной однородной совокупности, структурных изменений по тому или иному группировочному признаку. На основе структурных изменений изучаются закономерности общественных явлений.

Метод аналитической группировки заключается в исследовании взаимосвязей между факторными признаками в качественно однородной совокупности. С помощью аналитических группировок удается выявлять признаки, которые могут выступать или причиной, или следствием того или иного явления. В аналитических группировках чаще всего используются неравные интервалы.

Результаты группировочного материала оформляются в виде таблиц, где он излагается в наглядно-рациональной форме. Не всякая таблица может быть статистической. Табличные формы календарей, тестовых и опросных листов, таблица умножения не являются статистическими.

Статистическая таблица - это цифровое выражение итоговой характеристики всей наблюдаемой совокупности или ее составных частей по одному или нескольким существенным признакам. Статистическая таблица содержит два элемента: подлежащее и сказуемое.

Подлежащее статистической таблицы есть перечень групп или единиц, составляющих исследуемую совокупность единиц наблюдения.

Сказуемое статистической таблицы - это цифровые показатели, с помощью которых дается характеристика выделенных в подлежащем групп и единиц.

Различают простые, групповые и комбинационные таблицы.

В  простых таблицах, как правило, содержится справочный материал, где дается перечень групп или единиц, составляющих объект изучения. При этом части подлежащего не являются группами одинакового качества, отсутствует систематизация изучаемых единиц. Сказуемое этих таблиц содержит абсолютные величины, отражающие объемы изучаемых процессов.

Групповые и комбинационные таблицы предназначены для научных целей, где, в отличие от простых таблиц, в сказуемом - средние и относительные величины на основе абсолютных величин.

Групповая таблица - это таблица, где статистическая совокупность разбивается на отдельные группы по какому-либо одному существенному признаку, при этом каждая группа характеризуется рядом показателей. Примером такой группировки может быть разделение российских семей на группы по месту проживания (сельское и городское), где образуются подгруппы семей по количеству детей.

Комбинационная таблица - это таблица, где подлежащее представляет собой группировку единиц совокупности по двум и более признакам, которые распределяются на группы сначала по одному признаку, а затем на подгруппы по другому признаку внутри каждой из уже выделенных групп. Комбинационная таблица устанавливает существенную связь между факторами группировки.

Расчетная часть.

Тема:  Статистические методы изучения предприятий.

ЗАДАЧА 1. На основании данных выборочного обследования строительных предприятий региона (табл.1):

В графах «Форма соб-ти»: ф - федеральная, ч - частная, с - смешанная; «Стоим. ПФ» - стоимость производственных фондов в млн. руб.; «Объем вып.» - объем выпускаемой продукции в млн. руб.

Таблица 1.

№	Форма соб-ти	Стоим. ПФ	Число раб.	Объем вып.	№	Форма соб-ти	Стоим. ПФ	Число раб.	Объем вып.
1	ф	1102	295	452	12	с	93	226	43
2	ч	494	306	208	13	ч	660	452	295
3	с	854	432	353	14	ф	936	484	308
4	ч	730	512	412	15	ф	854	413	315
5	ф	680	487	296	16	с	1070	510	670
6	ч	673	405	433	17	ч	993	497	325
7	с	493	383	205	8	с	875	353	305
8	ч	230	204	190	19	ч	605	361	294
9	ф	774	454	336	20	ч	108	298	82
10	ч	534	306	420	21	с	776	420	460
11	с	86	240	57	22	ч	2340	598	1220

1. Провести группировку предприятий по численности занятых работников с равными интервалами и оптимальным числом групп и представить полученные данные в виде статистического ряда распределения и гистограммы. На основе гистограммы построить полигон, кумуляту и огиву распределения предприятий по численности работающих.

2. Составить и назвать статистические таблицы с комбинационным подле­жащим, представляющим собой группировку единиц совокупности по количест­венному признаку, каждая группа которой содержит подгруппы: а) также по коли­чественному признаку; б) по атрибутивному признаку. В обоих случаях использо­вать простое сказуемое, построенное по любому признаку. Формирование групп количественных признаков произвольное.

3. Сгруппировать предприятия: а) по формам собственности; б) но стоимости производственных фондов на 4 группы с равными интервалами. Определить для каждой группировки относительные показатели структуры и среднее число рабо­тающих для каждой группы предприятий.

4. Исчислить по сгруппированным выше (пункт За) данным среднее число работающих на предприятиях с помощью следующих средних (простых и взвешен­ных): а) арифметической; б) геометрической; в) гармонической.

5. Рассчитать показатели вариации числа работающих на предприятиях: а) по сгруппированным выше (пункт 36) данным с использованием средней арифметиче­ской простои и взвешенной; б) по несгруппированным данным.

6. Определить модальные и медианные значения численности работников предприятий а) по несгруппированным данным; б) из статистического ряда распре­деления (пункт I).

7. Определить для варианта 10%-ного выборочного наблюдения среднюю ошибку выборки для: а) среднего числа работающих на предприятиях; б) доли предприятий частной формы собственности с числом работающих более 300 чел. Указать с вероятностью 0,954 пределы возможных значений этих показателей в ге­неральной совокупности.

8. Вычислить параметры линейного уравнения регрессии для зависимости объема выпуска продукции предприятиями: а) от стоимости их производственных фондов; б) от числа работающих на них. Определить тесноту связи между призна­ками с помощью а) коэффициента корреляции знаков (коэффициента Фехнера); б) линейного коэффициента корреляции (коэффициента Пирсона).

ЗАДАЧА 2. Из данных о количестве экономических вузов региона, приведен­ных ниже:

Год	1994	1996	1998	2000	2002	2004
Кол-во вузов	32	42	46	54	78	49

1.Вычислить абсолютные и относительные (базисные и цепные) статистиче­ские показатели изменения уровней динамики данного ряда.

2. Рассчитать средние показатели динамики ряда.

3. Описать тенденцию ряда с помощью следующих методов сглаживания: а) механического выравнивания по трехлетней и пятилетней скользящим средним; б) аналитического выравнивания по уравнению линейного тренда.

ЗАДЧА 3. Из данных рыночной информации таблицы:

Таблица 2.

Средние цены на рынках города на различные товары (объем продаж указан в тыс. руб.)

Рынок	Товар
a	b	c
Цена/объем продаж	Цена/объем продаж	Цена/объем продаж
1999	2000	2001	1999	2000	2001	1999	2000	2001
A	80/3,4	85/3,6	87/3,7	50/2,9	52/3,1	55/3,7	20/5,4	30/5,6	37/5,5
B	92/2,1	95/2,5	98/2,7	58/2,6	60/2,8	62/2,9	40/5,3	48/5,4	65/4,6
C	75/3,2	78/3,4	86/3,0	47/3,2	48/3,5	52/4,2	15/6,8	19/6,9	28/7,1
D	62/3,8	65/3,9	70/4,1	42/4,0	45/3,8	45/3,7	11/7,7	12/7,5	16/7,3

Определить следующие цепные и базисные индексы:

1. Индивидуальные

а)     Физического объема товара «а» рынка В;

б)    Цен товара «с» рынка С;

в)     Товарооборота товара «а» рынка А.

2. Средних арифметических цен

а)     Товара «с» по рынкам A-D, взвешенных по товарообороту;

б)    Товаров «а», «b», «с» рынка В, взвешенных по объему продаж;

в)     Простых товара «а» в 1999-2001гг. (за базу принять рынок А).

3. Агрегатные физического объема рынка С.

Решение.

ЗАДАЧА 1.

На основании данных выборочного обследования строительных предприятий региона (табл.1):

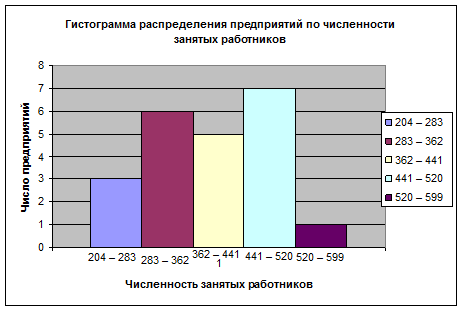
1. Провести группировку предприятий по численности занятых работников с равными интервалами и оптимальным числом групп и представить полученные данные в виде статистического ряда распределения и гистограммы. На основе гистограммы построить полигон, кумуляту и огиву распределения предприятий по численности работающих.

Решение:

Оптимальное количество групп определяем по формуле Стерджесса:

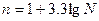
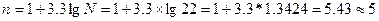
Величину равного интервала рассчитываем по формуле:

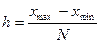
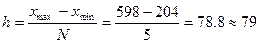
Обозначим границы групп:

204 – 283 – 1 группа,

283 – 362 – 2 группа,

362 – 441 – 3 группа,

441 – 520 – 4 группа,

520 – 599 – 5 группа.

Таблица 1.1

Группировка предприятий по численности занятых работников

№ группы	Численность занятых работников	Абсолютное число предприятий	Относительное, %
1	204 – 283	3	13,6
2	283 – 362	6	27,3
3	362 – 441	5	22,7
4	441 – 520	7	31,8
5	520 – 599	1	4,6
Итого	22	100

Представим полученные данные в виде гистограммы:

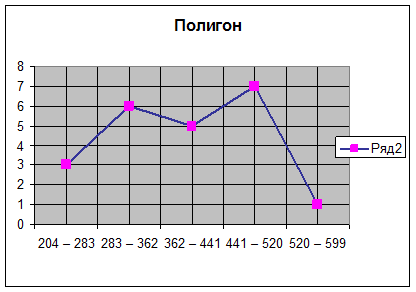
Полигона:

Кумуляты и Огивы:

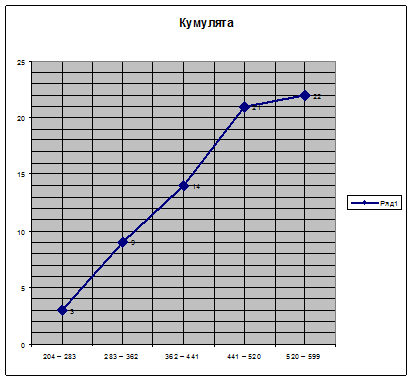
2. Составить и назвать статистические таблицы с комбинационным подле­жащим, представляющим собой группировку единиц совокупности по количест­венному признаку, каждая группа которой содержит подгруппы: а) также по коли­чественному признаку; б) по атрибутивному признаку. В обоих случаях использо­вать простое сказуемое, построенное по любому признаку. Формирование групп количественных признаков произвольное.

2а. По количественному признаку:

Таблица 1.2

Распределение объема выпуска продукции по стоимости производственных фондов и числу работников

Стоимость производственных фондов, млн.руб.	Число работников	Объем выпуска продукции, млн.руб.	Итог
43 - 435	436 - 828	829 - 1220
86 – 850	204 – 401	8	-	-	1
402 – 598	5	1	-	6
851 – 1600	204 – 401	1	1	-	2
402 – 598	4	1	-	5
1601 – 2340	204 – 401	-	-	-	-
402 – 598	-	-	1	1
Итог	18	3	1	22

2б. По атрибутивному признаку:

Таблица 1.3

Распределение объема выпуска продукции по стоимости производственных фондов и форме собственности

Стоимость производственных фондов, млн.руб.	Форма собственности	Объем выпуска продукции, млн.руб.	Итог
43 - 300	301 - 600	601 - 1220
86 – 850	Ф	1	1	-	2
Ч	4	3	-	7
С	4	1	-	5
851 – 1600	Ф	-	3	-	3
Ч	-	1	-	1
С	-	2	1	3
1601 – 2340	Ф	-	-	-	-
Ч	-	-	1	1
С	-	-	-	-
Итог	9	11	2	22

3. Сгруппировать предприятия: а) по формам собственности; б) по стоимости производственных фондов на 4 группы с равными интервалами. Определить для каждой группировки относительные показатели структуры и среднее число рабо­тающих для каждой группы предприятий.

а) по формам собственности:

                      Таблица 1.4

Форма собственности	Количество предприятий	Среднее число рабочих
Абсолют.	Относит.,%
Ф	5	22,7	427
Ч	10	45,5	394
С	7	31,8	366
Итог	22	100	-

б) По стоимости производственных фондов:

Таблица 1.5

Стоимость производственных фондов	Количество предприятий	Среднее число работников
Абсолют.	Относит.,%
86 – 650	8	36,4	291
651 – 1215	13	59,1	440
1216 – 1780	-	-	-
1781 – 2340	1	4,5	598
Итог	22	100	-

4. Исчислить по сгруппированным выше (пункт За) данным среднее число работающих на предприятиях с помощью следующих средних (простых и взвешен­ных): а) арифметической; б) геометрической; в) гармонической.

а)     ;

;  .

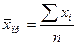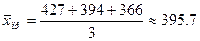
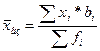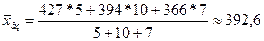б)    ;

;

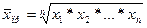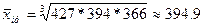
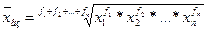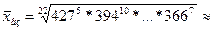
в) ;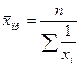

.

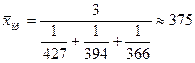
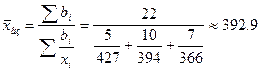5. Рассчитать показатели вариации числа работающих на предприятиях: а) по сгруппированным выше (пункт 36) данным с использованием средней арифметиче­ской простои и взвешенной; б) по несгруппированным данным.

а) С использованием средней арифметической простой:

№	Ст-ть ПФ
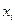
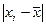
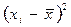
1	86 – 650	291	41,3	1705,7
2	651 – 1215	440	107,7	11599,3
3	1216 – 1780	-	-	-
4	1781 – 2340	598	265,7	70596,5
Итого	1329	414,7	171976,1

;

;

;

;

;

;

;

.

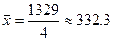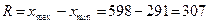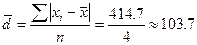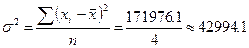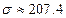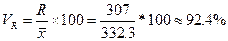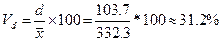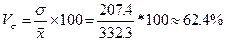С использованием средней арифметической взвешенной:

№	Ст-ть ПФ
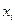
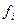
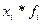
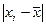
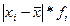
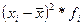
1	86 – 650	291	8	2328	230,6	1844,8	425410,9
2	651 – 1215	440	13	5720	379,6	4934,8	1873250
3	1216 – 1780	-	-	-	-	-	-
4	1781 – 2340	598	1	598	537,6	537,6	289013,8
Итого	1329	22	-	-	7317,2	2587674,7

;

;

;

;

;

;

.

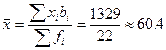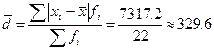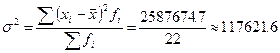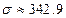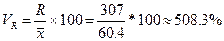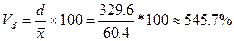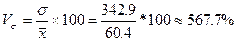б) по несгруппированным данным.

№
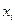
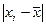
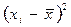
1	295	97,5	9515,1
2	306	86,5	7490,1
3	432	39,5	1556,7
4	512	119,5	14269,4
5	487	94,5	8921,7
6	405	12,5	155,1
7	383	9,5	91,1
8	204	188,5	35549,4
9	454	61,5	3776,7
10	306	86,5	7490,1
11	240	152,5	23270,1
12	226	166,5	27737,4
13	452	59,5	3534,8
14	484	91,5	8363,9
15	413	20,5	418,4
16	510	117,5	13795,6
17	497	104,5	10910,8
18	353	39,5	1563,8
19	361	31,5	995,1
20	298	94,5	8938,8
21	20	27,5	753,8
22	598	205,5	42211,6
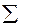
	8636	1907	231309,5

;

;

;

;

;

;

;

.

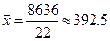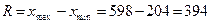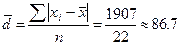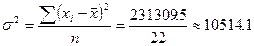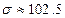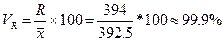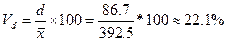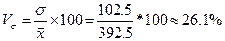6. Определить модальные и медианные значения численности работников предприятий а) по несгруппированным данным; б) из статистического ряда распре­деления (пункт I).

а) По несгруппированным данным.

204,226,240,295,298,306,306,353,361,383,405,413,420,432,452,454,484,487,497,510,512,598.

,

.

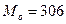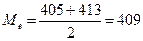б) из статистического ряда распре­деления (пункт I).

1	204 – 283	3	3
2	283 – 362	6	9
3	362 – 441	5	14
4	441 – 520	7	21
5	520 – 599	1	22

,

.

,

.

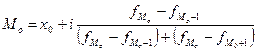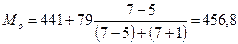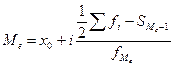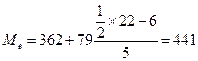7. Определить для варианта 10%-ного выборочного наблюдения среднюю ошибку выборки для: а) среднего числа работающих на предприятиях; б) доли предприятий частной формы собственности с числом работающих более 300 чел. Указать с вероятностью 0,954 пределы возможных значений этих показателей в ге­неральной совокупности.

а) среднего числа работающих на предприятиях.

,

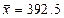
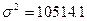
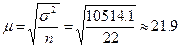По теореме Ляпунова t=2,

,

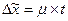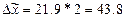
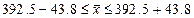
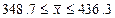
При среднем числе работающих на предприятии выборке равной 392,5 чел., значение среднего числа работающих в генеральной совокупности будет находится в пределах от 348,7 до 436,3 человек вероятность 95,4%.

.

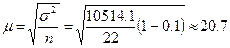
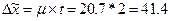
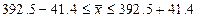
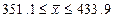б) доли предприятий частной формы собственности с числом работающих более 300 чел.

2 – 306 ,4 – 512, 6 – 405, 10 – 306, 13 – 452, 17 – 497, 19 – 361, 22 – 598

,

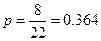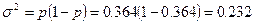
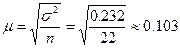
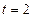
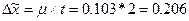
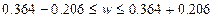
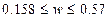
При доли предприятий частной формы собственности с числом работающих более 300 человек в выборке равной 36,4%, доля таких предприятий в генеральной совокупности будет находится в пределах от 15,8% до 57%.

Для бесповторной выборки:

.

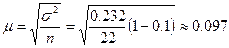
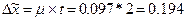
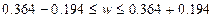
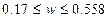
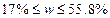8. Вычислить параметры линейного уравнения регрессии для зависимости объема выпуска продукции предприятиями: а) от стоимости их производственных фондов; б) от числа работающих на них. Определить тесноту связи между призна­ками с помощью а) коэффициента корреляции знаков (коэффициента Фехнера); б) линейного коэффициента корреляции (коэффициента Пирсона).

а) от стоимости их производственных фондов

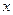
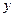
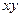
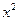
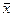
1102	452	498104	1214404	529,72
494	208	102752	244036	237,88
854	353	301462	729316	410,68
730	412	300760	532900	351,16
680	296	201280	462400	327,16
673	433	291409	452929	323,8
493	205	101065	243049	237,4
230	190	43700	52900	111,16
774	336	260064	599076	372,28
534	420	224280	285156	257,08
86	57	4902	7396	42,04
93	43	3999	8649	45,4
660	295	194700	435600	317,56
936	308	288288	876096	450,04
854	315	269010	729316	410,68
1070	670	716900	1144900	514,36
993	325	322725	986049	477,4
875	305	266875	765625	420,76
605	294	177870	366025	291,16
108	82	8856	11664	52,6
776	460	356960	602176	373,24
2340	1220	2854800	5475600	1123,96
15960	7679	7790761	16225262	7677,52

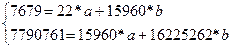
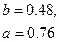
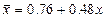
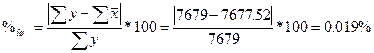
Определить тесноту связи между призна­ками с помощью:

а) коэффициента корреляции знаков (коэффициента Фехнера):

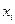
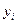
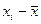
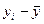
№					с/н
1	1102	452	+	+	С
2	494	208	-	-	С
3	854	353	+	+	С
4	730	412	+	+	С
5	680	296	-	-	С
6	673	433	-	+	Н
7	493	205	-	-	С
8	230	190	-	-	С
9	774	336	+	-	Н
10	534	420	-	+	Н
11	86	57	-	-	С
12	93	43	-	-	С
13	660	295	-	-	С
14	936	308	+	-	Н
15	854	315	+	-	Н
16	1070	670	+	+	С
17	993	325	+	-	Н
18	875	305	+	-	Н
19	605	294	-	-	С
20	108	82	-	-	С
21	776	460	+	+	С
22	2340	1220	+	+	С
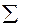
	15960	7679

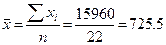
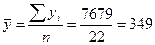
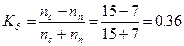 - Связь близка к прямой.

б) линейного коэффициента корреляции (коэффициента Пирсона):

№
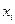
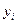
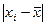
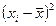
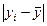
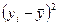
1	1102	452	376,5	141752,3	103	10609
2	494	208	231,5	53592,25	141	19881
3	854	353	128,5	16512,25	4	16
4	730	412	4,5	20,25	63	3969
5	680	296	45,5	2070,25	53	2809
6	673	433	52,5	2756,25	84	7056
7	493	205	232,5	54056,25	144	20736
8	230	190	495,5	245520,3	159	25281
9	774	336	48,5	2352,25	13	169
10	534	420	191,5	36672,25	71	5041
11	86	57	639,5	408960,3	292	85264
12	93	43	632,5	400056,3	306	93636
13	660	295	65,5	4290,25	54	2916
14	936	308	210,5	44310,25	41	1681
15	854	315	128,5	16512,25	34	1156
16	1070	670	344,5	118680,3	321	103041
17	993	325	267,5	71556,25	24	576
18	875	305	149,5	22350,25	44	1936
19	605	294	120,5	14520,25	55	3025
20	108	82	617,5	381306,3	267	71289
21	776	460	50,5	2550,25	111	12321
22	2340	1220	1614,5	2606610	871	758641
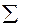
	15960	7679	-	4647008	-	1231049

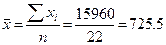
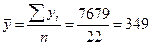
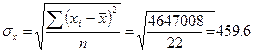
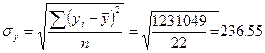
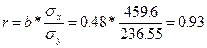 - Связь сильная, прямая.

б) от числа работающих на них

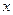
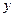
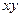
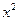
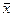
295	452	133340	87025	195,92
306	208	63648	93636	213,19
432	353	152496	186624	411,01
512	412	210944	262144	536,61
487	296	144152	237169	497,36
405	433	175365	164025	368,62
383	205	78515	146689	334,08
204	190	38760	41616	53,05
454	336	152544	206116	445,55
306	420	128520	93636	213,19
240	57	13680	57600	109,57
226	43	9718	51076	87,59
452	295	133340	204304	442,41
484	308	149072	234256	492,65
413	315	130095	170569	381,18
510	670	341700	260100	533,47
497	325	161525	247009	513,06
353	305	107665	124609	286,98
361	294	106134	130321	299,54
298	82	24436	88804	200,63
420	460	193200	176400	392,17
598	1220	729560	357604	671,63
8636	7679	3378409	3621332	7679,46

.

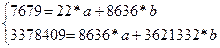
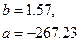
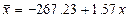
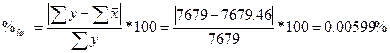Определить тесноту связи между призна­ками с помощью:

а) коэффициента корреляции знаков (коэффициента Фехнера):

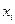
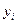
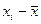
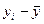
№					с/н
1	295	452	-	+	Н
2	306	208	-	-	С
3	432	353	+	+	С
4	512	412	+	+	С
5	487	296	+	-	Н
6	405	433	+	+	С
7	383	205	-	-	С
8	204	190	-	-	С
9	454	336	+	-	Н
10	306	420	-	+	Н
11	240	57	-	-	С
12	226	43	-	-	С
13	452	295	+	-	Н
14	484	308	+	-	Н
15	413	315	+	-	Н
16	510	670	+	+	С
17	497	325	+	-	Н
18	353	305	-	-	С
19	361	294	-	-	С
20	298	82	-	-	С
21	420	460	+	+	С
22	598	1220	+	+	С
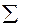
	8636	7679

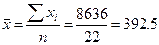
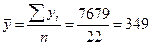
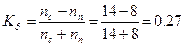 - Связь близка к прямой.

б) линейного коэффициента корреляции (коэффициента Пирсона):

№
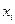
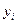
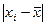
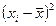
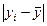
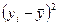
1	295	452	97,5	9506,25	103	10609
2	306	208	86,5	7482,25	141	19881
3	432	353	39,5	1560,25	4	16
4	512	412	119,5	14280,25	63	3969
5	487	296	94,5	8930,25	53	2809
6	405	433	12,5	156,25	84	7056
7	383	205	9,5	90,25	144	20736
8	204	190	188,5	35532,25	159	25281
9	454	336	61,5	3782,25	13	169
10	306	420	86,5	7482,25	71	5041
11	240	57	152,5	23256,25	292	85264
12	226	43	166,5	27722,25	306	93636
13	452	295	59,5	3540,25	54	2916
14	484	308	91,5	8372,25	41	1681
15	413	315	20,5	420,25	34	1156
16	510	670	117,5	13806,25	321	103041
17	497	325	104,5	10920,25	24	576
18	353	305	39,5	1560,25	44	1936
19	361	294	31,5	992,25	55	3025
20	298	82	94,5	8930,25	267	71289
21	420	460	27,5	756,25	111	12321
22	598	1220	205,5	42230,25	871	758641
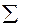
	8636	7679	-	231309,5	-	1231049

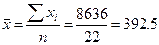
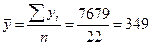
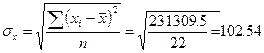
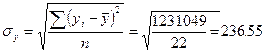
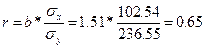 - Связь умеренная, прямая.

ЗАДАЧА 2. Из данных о количестве экономических вузов региона, приведен­ных ниже:

Год	1994	1996	1998	2000	2002	2004
Кол-во вузов	32	42	46	54	78	49

1.Вычислить абсолютные и относительные (базисные и цепные) статистиче­ские показатели изменения уровней динамики данного ряда.

2. Рассчитать средние показатели динамики ряда.

3. Описать тенденцию ряда с помощью следующих методов сглаживания: а) механического выравнивания по трехлетней и пятилетней скользящим средним; б) аналитического выравнивания по уравнению линейного тренда.

1.

Год	Y(кол-во вузов		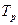(%)	(%)	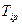A%
в	ц	в	ц	в	ц
1994	32	-	-	-	-	-	-	-
1996	42	10	10	131,3	131,3	31,3	31,3	0,32
1998	46	4	14	109,5	143,8	9,5	43,8	0,42
2000	54	8	22	117,4	168,8	17,4	68,8	0,46
2002	78	24	46	144,4	243,8	44,4	143,8	0,54
2004	49	-29	17	62,8	153,1	-37,2	53,1	0,78

2. ,

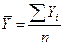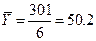
Средний абсолютный прирост:

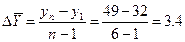
Средний темп роста:

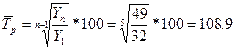
Средний темп прироста:

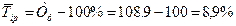
3.

а) Исчислим трехлетние скользящие средние уровня ряда за 1994 – 1998 гг.:

;

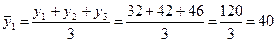За 1996 – 2000 гг.:

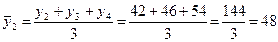 и т.д.

Исчислим пятилетние скользящие средние уровня ряда за 1994 – 2002 гг.:

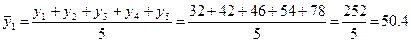 и т.д.

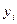
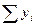
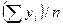
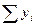
Год	Кол-во вузов	Скользящие трехлетние суммы	Трехлетние скользящие средние	Скользящие пятилетние суммы	Пятилетние скользящие средние
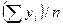
1994	32	-	-	-	-
1996	42	120	40	252	50,4
1998	46	144	48	269	53.8
2000	54	178	59,3	-	-
2002	78	181	60,3	-	-
2004	49	-	-	-	-

б) аналитического выравнивания по уравнению линейного тренда

Уравнение прямой имеет вид: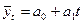

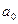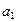Для нахождения  и  необходимо решить систему нормальных уравнений

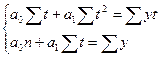
Год	Кол-во вузов
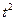
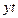
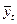
1994	32	-5	25	-160	35,82
1996	42	-3	9	-126	41,56
1998	46	-1	1	-46	47,3
2000	54	+1	1	54	53
2002	78	+3	9	234	58,78
2004	49	+5	25	245	64,52
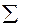
	301	0	70	201	300,98

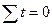,система нормальных уравнений принимает вид:

;     .

;

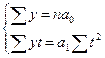
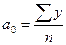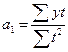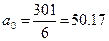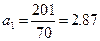
Уравнение прямой будет иметь вид: .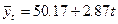

Подставив в это уравнение значение t,получим выровненные теоретические значения .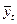

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗАДЧА 3. Из данных рыночной информации таблицы:

Средние цены на рынках города на различные товары

(объем продаж указан в тыс. руб.)

Рынок	Товар
a	b	c
Цена/объем продаж	Цена/объем продаж	Цена/объем продаж
1999	2000	2001	1999	2000	2001	1999	2000	2001
A	80/3,4	85/3,6	87/3,7	50/2,9	52/3,1	55/3,7	20/5,4	30/5,6	37/5,5
B	92/2,1	95/2,5	98/2,7	58/2,6	60/2,8	62/2,9	40/5,3	48/5,4	65/4,6
C	75/3,2	78/3,4	86/3,0	47/3,2	48/3,5	52/4,2	15/6,8	19/6,9	28/7,1
D	62/3,8	65/3,9	70/4,1	42/4,0	45/3,8	45/3,7	11/7,7	12/7,5	16/7,3

Определить следующие цепные и базисные индексы:

1. Индивидуальные

а)     Физического объема товара «а» рынка В;

б)    Цен товара «с» рынка С;

в)     Товарооборота товара «а» рынка А.

2. Средних арифметических цен

а)     Товара «с» по рынкам A-D, взвешенных по товарообороту;

б)    Товаров «а», «b», «с» рынка В, взвешенных по объему продаж;

в)     Простых товара «а» в 1999-2001гг. (за базу принять рынок А).

3. Агрегатные физического объема рынка С.

1. Индивидуальные

а) Физического объема товара «а» рынка В:

1999	2000	2001
p	q	p	q	p	Q
90	2.1	95	2.5	98	2.7

Цепные индексы:

,

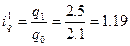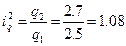
Базисные индексы:

,

.

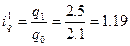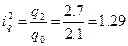б) Цен товара «с» рынка С:

1999	2000	2001
p	q	p	q	p	Q
15	6,8	19	6,9	28	7,1

Цепные индексы:

,

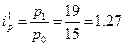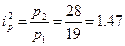
Базисные индексы:

,

.

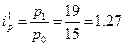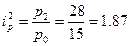в) Товарооборота товара «а» рынка А:

1999	2000	2001
p	q	p	q	p	Q
80	3,4	85	3,6	87	3,7

Цепные индексы:

,

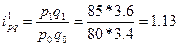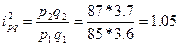
Базисные индексы:

.

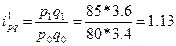
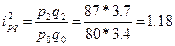2. Средних арифметических цен

а) Товара «с» по рынкам A-D, взвешенных по товарообороту

Рынок	1999	2000	2001
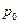
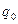
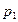
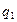
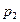
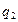
А	20	5,4	30	5,6	37	5,5
В	40	5,3	48	5,4	65	4,6
С	15	6,8	19	6,9	28	7,1
Д	11	7,7	12	7,5	16	7,3

Базисные:

, ;

,

.

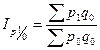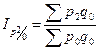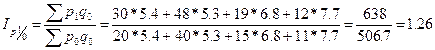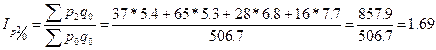Цепные:

, ;

,

.

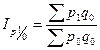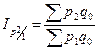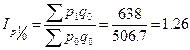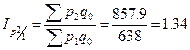б)Товаров «а», «b», «с» рынка В, взвешенных по объему продаж;

а	b	c
1999	2000	2001	1999	2000	2001	1999	2000	2001
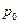
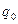
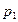
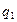
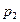
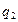
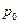
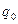
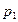
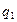
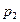
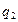
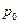
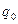
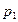
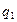
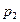
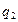
92	2,1	95	2,5	98	2,7	58	2,6	60	2,8	62	2,9	40	5,3	48	5,4	65	4,6

Базисные:

, ;

,

.

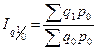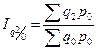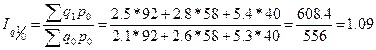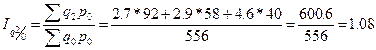Цепные:

, ;

,

.

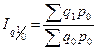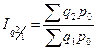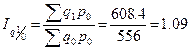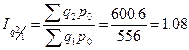в)Простых товара «а» в 1999-2001гг. (за базу принять рынок А)

	1999	2000	2001
А(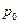)	80	85	87
В(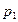)	92	95	98
С(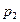)	75	78	86
D(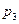)	62	65	70

Базисные:

,

,

.

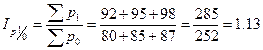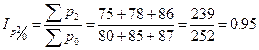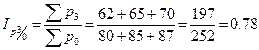Цепные:

,

,

.

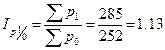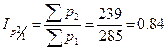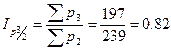3. Агрегатные физического объема рынка С.

а	b	c
1999	2000	2001	1999	2000	2001	1999	2000	2001
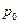
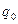
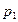
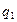
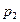
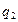
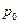
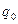
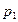
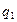
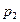
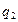
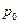
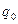
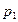
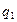
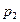
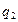
75	3,2	78	3,4	86	3,0	47	3,2	48	3,5	52	4,2	15	6,8	19	6,9	28	7,1

Цепные:

,;

,

.

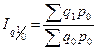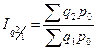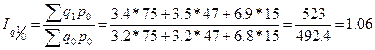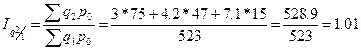Базисные:

, .

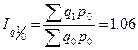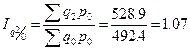Заключение

Группировка – это распределение единиц совокупности по группам в соответствии со следующим принципом: различия между единицами, отнесенными к одной группе должны быть меньше, чем между единицами, отнесенными к разным группам. Сводные показатели для отдельных групп считаются устойчивыми и типичными, если они удовлетворяют двум основным принципам:

1.     Группировка должна быть проведена правильно, для чего устанавливают правила отнесения единицы к одной или другой группе;

2.     Группы должны иметь достаточную численность.

Обязательно, при группировке, используют характеристику, по которой будет проводиться эта группировка – группировочный признак. Для того чтобы отделить одну группу от другой применяют интервалы группировки. Расчленение совокупностей единиц по группам производятся:

1.     По одному признаку, т.е. простая группировка (монотетическая);

2.     По двум или более признакам, т.е. сложная группировка (комбинационная, политетическая).

По сравнению с простыми комбинационные группировки обладают дополнительными аналитическими свойствами.

Признак, по которому производится образование групп, называется группировочным признаком или основанием группировки. Выбор ее зависит от решения конкретной задачи. Для образования групп обычно устанавливают интервалы.

 Для изучения силы (тесноты) связей между факторными и результативными признаками исчисляют эмпирические корреляционные отношения. Для этого надо иметь четкое представление по факторным и результативным признакам. Если каждому значению величины факторного признака соответствует только одно результативного признака, то такая связь между величинами называется функциональной. Эти связи выражаются формулами  и широко применяются в математике, физике, астрономии.

В экономических явлениях проявляется зависимость распределения значений результативного признака от нескольких значений факторов. Такого рода связи называются стохастическими. В частном случае стохастической является корреляционная связь. При этой связи одному и тому же значению факторного признака, могут соответствовать самые различные значения результативного признака.

Список использованной литературы:

1.                Гусаров В.М., «Теория статистики», – М.: Аудит, ЮНИТИ, 1998;

2.                «Общая теория статистики»:Учеб. Пособие/ Под ред. Р.А. Шмойловой.- М.: Финансы и статистика, 2002.

3.                «Практикум по теории статистики»:Учеб. Пособие/ Под ред. Р.А. Шмойловой.- М.: Финансы и статистика, 2003;

4.                 «Практикум по статистике: Учеб. пособие для вузов» / Под ред.  В. М. Симчеры / ВЗФЭИ. – М.: ЗАО «Финстатинформ», 1999;

5.                Лекции по теории статистики, Лазурин Е.А.

6.                Сиденко Анатолий Викторович «Общая теория статистики» http://oknedis.narod.ru/