Задача 1.
Найти общее решение дифференциального уравнения xy’–y=x3sinx и его частное решение, определенное начальными данными y(π/2)=0.
Решение.
xy’–y=x3sinx
Найдем решение однородного уравнения.
xy’–y=0
![]()
![]()
![]()
lny=lnx+C
y=Cx
Решение исходного уравнения найдем методом вариации постоянной.
C=C(x)
y' = C+C’x
x(C+C’x)–Cx=x3sinx
Cx+C’x2–Cx=x3sinx
C’x2 =x3sinx
C’ =xsinx
C = ![]() =
= ![]() = –xcosx +
= –xcosx + ![]() = –xcosx + sinx +C1
= –xcosx + sinx +C1
y = Cx = –x2cosx + xsinx + xC1
Найдем частное решение, определяемое начальными условиями.
y(π/2)=0
y(π/2) = –(π/2)2cos(π/2) + (π/2)sin(π/2) + (π/2)C1 = π/2+(π/2)C1 = 0
C1 = –1
Получаем частное решение: y = –x2cosx + xsinx – x
Задача 2.
Найти общее решение дифференциального уравнения yy’’–y’2=yy’, и его частное решение, определенное начальными данными y(0)=1; y’(0)=1.
Решение.
Обозначим y' = p(y)
Тогда y”=pp’
Получим следующее:
ypp’ – p2 = yp
yp’ – p = y
Найдем решение однородного уравнения.
yp’ – p = 0
![]()
![]()
![]()
lnp=lny+C
p=Cy
Решение уравнения yp’ – p = y найдем методом вариации постоянной.
C=C(y)
p' = C+C’y
y(C+C’y)–Cy=y
Cy+C’y2–Cy=y
C’y2 =y
![]()
C = lny + C1
p = Cy = ylny + C1y
y’ = ylny + C1y
![]()
![]()
ln(lny + C1) = x+C2
lny + C1 = C2ex
![]()
Найдем частное решение, удовлетворяющее начальным условиям.
![]()
y(0) = 1
![]()
![]()
y’(0) = 1
![]()
C2 = 1
C1 = e–1
Получили частное решение:
![]()
Задача 3.
Найти общее решение дифференциального уравнения y’’+2y’–3y=ex, и его частное решение, определенное начальными данными y(0)=0, y’(0)=2.
Решение
Найдем общее решение однородного уравнения.
Характеристическое уравнение.
k2+2k–3=0
k1,2=–1,3
y(общее однородное)=c1e–x+c2e3x
Частное решение неоднородного уравнения будем искать в виде:
y = (Ax2+Bx+C)xex = (Ax3+Bx2+Cx)ex.
y’ = (Ax3+Bx2+Cx)ex + (3Ax2+2Bx+C)ex = (Ax3+(B+3A)x2+(2B+C)x+C)ex
y” = (Ax3+(B+3A)x2+(2B+C)x+C)ex + (3Ax2+(2B+6A)x+(2B+C))ex = (Ax3+(B+6A)x2+(6A+4B+C)x+2B+2C)ex
y’’+2y’–3y = Ax3+Bx2+Cx + 2(Ax3+(B+3A)x2+(2B+C)x+C) – 3(Ax3+(B+6A)x2+(6A+4B+C)x+2B+2C) ex = ((3B+9A)x2+(6A+6B+4C)x+2B+3C) ex = ex
Приравнивая множители при степенях х, получим систему уравнений
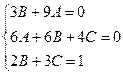
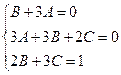
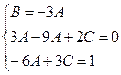
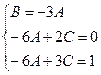
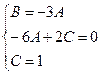
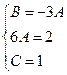
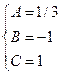
Следовательно, частное решение неоднородного уравнения имеет вид:
y(частное неоднородное)= y = ((1/3)x3–x2+x)ex
Общее решение исходного дифференциального уравнения имеет вид:
y=c1e–4x+c2e2x+((1/3)x3–x2+x)ex
Найдем частное решение, удовлетворяющее начальным условиям.
y' = –4c1e–4x+2c2e2x+((1/3)x3–x2+x+x2–2x+1)ex = –4c1e–4x+2c2e2x+((1/3)x3–x+1)ex
y(0) = c1+c2
y’(0) = –4c1+2c2+1
Получаем систему уравнений:
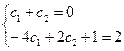
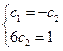
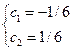
Получаем частное решение, удовлетворяющее начальным условиям:
y=(–1/6)e–4x+(1/6)e2x+((1/3)x3–x2+x)ex
Задача 4.
Найти общее
решение дифференциального уравнения ![]() .
.
Решение.
Найдем общее решение однородного уравнения.
y"+ Решение.
Найдем общее решение однородного уравнения.
y"+10y’+25y=0
Характеристическое уравнение.
k2+4k+25=0
k=–5, корень кратности 2.
Общее решение однородного уравнения
yоо=(c1+c2x)e–5x
y1=e–5x y2=xe–5x
y1’=–5e–5x y2’= e–5x –5xe–5x
Применяя метод вариации постоянной, получим:
c1’ e–5x +c2’x e–5x =0
–c1’5 e–5x +c2’(e–5x–5x
e–5x)= ![]()
Умножив первое уравнение на (–5) и вычтя из второго, получим:
![]()
![]()
![]() =
= ![]() = –2x–3+C02 =
= –2x–3+C02 = ![]()
c1’ e–5x +c2’x e–5x =0
![]()
![]()
![]()
![]() =
= ![]() = 3x–3+C01 =
= 3x–3+C01 = ![]()
Получаем общее решение дифференциального уравнения:
![]() =
= ![]() =
= ![]()
Задача 5.
Решить систему
линейных однородных дифференциальных уравнений первого порядка с постоянными
коэффициентами, определенными матрицей 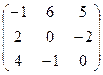 при начальных условиях неизвестных, определенных столбцом
значений
при начальных условиях неизвестных, определенных столбцом
значений ![]() в нулевой начальный момент времени.
в нулевой начальный момент времени.
Решение.
Найдем собственные числа матрицы.
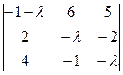 =(–1–λ)
=(–1–λ)![]() – 6
– 6![]() + 5
+ 5![]() =
=
(–1–λ)(λ2–2) – 6(–2λ+8) + 5(–2+4λ) = – λ2 – λ3 +2+2λ +12λ–48 – 10+20λ =– λ3 – λ2 +34λ – 56.
Получили характеристическое уравнение λ3+λ2–34λ+56=0.
Решив его, получим собственные числа λ1,2,3=2;4;–7.
Найдем собственные вектора матрицы.
Собственный вектор, соответствующий собственному значению λ=2.
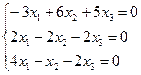
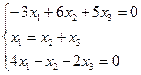
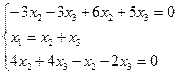
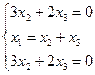
Получаем
собственный вектор ![]() .
.
Собственный вектор, соответствующий собственному значению λ=4.
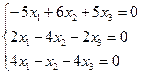
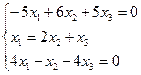
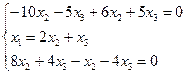

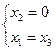
Получаем
собственный вектор ![]() .
.
Собственный вектор, соответствующий собственному значению λ=–7.
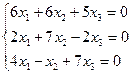
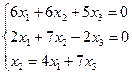
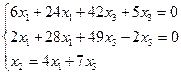
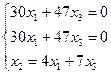
Получаем
собственный вектор ![]() .
.
Получаем общее решение системы:
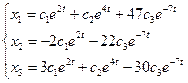
Для того, чтобы найти частное решение системы, нужно решить систему уравнений:
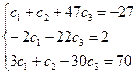
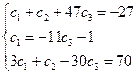
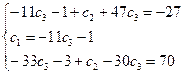
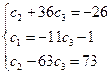
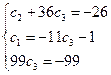
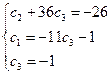
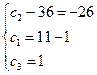
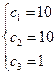
Следовательно, частное решение системы уравнений, удовлетворяющее начальным условиям равно
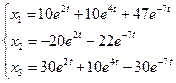 .
.
Задача 6.
Найти кривую, проходящую через точку (1,0), для которой отрезок, отсекаемый на оси ординат Oy касательной равен модулю радиус-вектора точки касания.
y=y(x)
Уравнение касательной
x–x0=x’(y0)(y–y0)
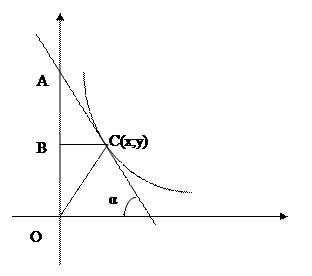
OC=![]()
BC=x
y'(x)= 1/tg α
x'(y)= tg α
AB=BC∙tg(α)
![]()
![]()
z=x2+y2
![]()
z’ = 2xx’
![]()
![]()
Найдем решение однородного уравнения.
![]()
![]()
![]()
![]()
![]()
Постоянную С найдем из условия, что кривая проходит через точку (1;0)
![]()
![]()
![]()
C=0; C=–2
![]()