ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ И НАУКЕ РОССИЙСКОЙ
ФЕДЕРАЦИИ
ГОУ ВПО
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ
ИНСТИТУТ
СЕРПУХОВСКОЕ ПРЕДСТАВИТЕЛЬСТВО
К О Н Т Р О Л Ь Н А Я
Р А Б О Т А
№ 3
по дисциплине «Теория вероятностей и математическая
статистика»
Исполнитель:
специальность
Ф и К
курс ФНО
группа
№ зачетной
книжки
Руководитель:
г. Серпухов
2007
1. При разрыве бронебойного снаряда 20% от общего
числа составляют крупные осколки, 30% – средние и 50% – мелкие. Крупный осколок
пробивает броню танка с вероятностью 0.8, средний – с вероятностью 0.5, а
мелкий осколок – с вероятностью 0.2.
а) Найти
вероятность того, что в броне танка образовалась пробоина.
б) В
результате испытания бронебойного снаряда броня танка оказалась пробитой.
Какова вероятность того, что пробоина образовалась от мелкого осколка?
Решение:
а) 
б) 
2. Вероятность того, что деталь не проверялась
ОТК, равна 0.2. Найти вероятность того, что среди 400 случайно отобранных
деталей окажется от 70 до 100 деталей, не проверенных ОТК.
Решение:
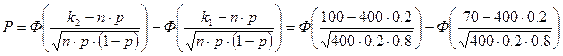
3. Баскетболист попадает в корзину с вероятностью
0.7. Составить закон распределения числа попаданий, если выполнено 4 броска.
Построить график функции распределения этой случайной величины.
Решение:
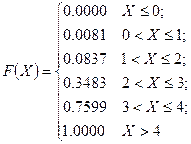
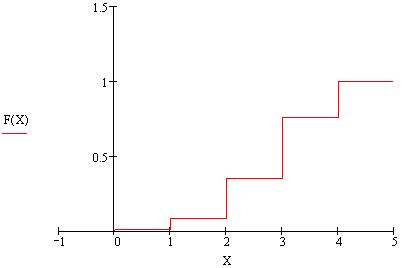
4. Случайная величина 
распределена по закону
Пуассона с параметром 
.
Необходимо:
а) выписать формулу для вычисления вероятности 
;
б) найти вероятность 
;
в) найти математическое ожидание 
и дисперсию 
.
Решение:
а) 
б)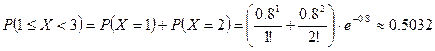 
в) 
5. Среднее значение длины детали равно
50 см. Пользуясь леммой Чебышева (неравенством Маркова), оценить вероятность того,
что случайно взятая деталь окажется по длине:
а) более
49.5 см.;
б) не
более 50.5 см.
Решение:
а) 
б) 
Список используемой литературы:
1. Кремер Н.Ш. – Теория вероятностей м
математическая статистика: Учебник для вузов. – 2-е изд., перераб.
и доп. – М.: ЮНИТИ-ДАНА, 2003. – 573 с.