9. Найти решение системы алгебраических линейных уравнений:
а) по правилу Крамера; б) матричным методом.
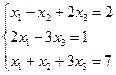
Найдем определитель матрицы, состоящей из коэффициентов при
неизвестных.
Δ = 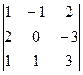 =
= 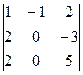 =
= 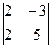 = 16 ≠ 0,
следовательно, система уравнений имеет единственное решение.
= 16 ≠ 0,
следовательно, система уравнений имеет единственное решение.
а) Решим систему по правилу Крамера:
Δ1 = 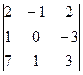 =
= 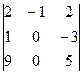 =
= 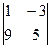 = 32.
= 32.
Δ2 = 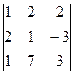 = 1 ∙
= 1 ∙ 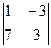 – 2 ∙
– 2 ∙ 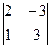 + 2 ∙
+ 2 ∙ 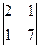 = 1∙24 – 2∙9 + 2∙13 = 24 – 18 + 26 = 32.
= 1∙24 – 2∙9 + 2∙13 = 24 – 18 + 26 = 32.
Δ3
= 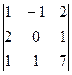 =
= 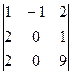 =
= 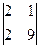 = 16.
= 16.
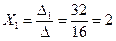
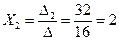
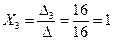
Подставим найденные значения в уравнения системы.
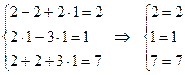
Так как все уравнения системы обратились в равенства, то
решение найдено верно.
б) Решим систему матричным способом.
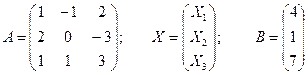
X=A-1∙B
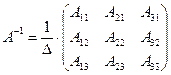
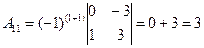
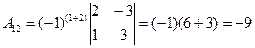
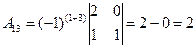

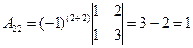
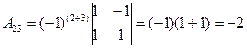
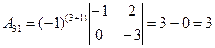
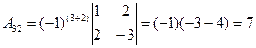
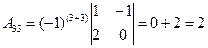
В результате получаем:
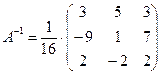
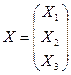 =
= 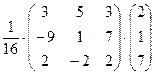 =
= 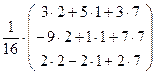 =
= 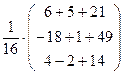 =
= 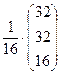 =
= 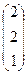 .
.
15. Пользуясь методом исключения неизвестных, найти общее
решение системы линейных уравнений, а так же два частных ее решения, одно из
которых базисное.
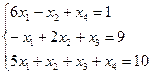
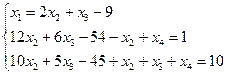
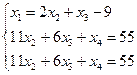
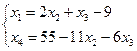
Мы получили общее решение данной системы.
Базисное решение системы линейных уравнений получается при
присвоении свободным переменным значения 0.
Получим базисное решение системы
X2=0; X3=0; X1=–9; X4=55
Найдем частное решение при
X2=1,
X3=1 Получим
X2=1; X3=1; X1=–6; X4=38
21. Решить задачу линейного программирования: а)
симплекс-методом; б) графически.
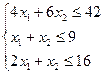
x1≥0;
x2≥0
Z=7x1+8x2→max
а) Решим задачу симплекс-методом.
Для этого сначала приведем модель к каноническому виду,
когда система ограничений имеет вид уравнений. Это достигается введением дополнительных
переменных. Получим систему:
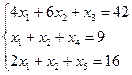
x1≥0;
x2≥0; x3≥0; x4≥0; x5≥0
Z=7x1+8x2→max
Решим систему уравнений, выразив переменные x3, x4, x5 через
переменные x1,
x2.
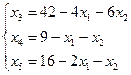
x1≥0;
x2≥0; x3≥0; x4≥0; x5≥0
Z=7x1+8x2→max
Если присвоить свободным переменным x1 и x2 значение 0, то получим
опорный план:
x1=0;
x2=0; x3=42; x4=9; x5=16.
Решение ЗЛП симплекс-методом осуществляется с помощью
симплекс-таблиц.
Составим симплекс-таблицу, соответствующую найденному
опорному плану.
|
Б.п.
|
1
|
–X1
|
–X2
|
|
X3 =
|
42
|
4
|
6
|
|
X4 =
|
9
|
1
|
1
|
|
X5 =
|
16
|
2
|
1
|
|
Z =
|
0
|
–7
|
–8
|
Этот опорный план не является оптимальным, т.к. в Z-строке имеются
отрицательные элементы.
Ключевым столбцом будет столбец x2.
Ключевой строкой будет строка x3.
После преобразования, получим следующий опорный план:
|
Б.п.
|
1
|
–X1
|
–X3
|
|
X2 =
|
7
|
2/3
|
1/6
|
|
X4 =
|
2
|
1/3
|
–1/6
|
|
X5 =
|
9
|
4/3
|
–1/6
|
|
Z =
|
56
|
–5/3
|
4/3
|
Этот опорный план не является оптимальным, т.к. в Z-строке имеются
отрицательные элементы.
Ключевым столбцом будет столбец x1.
Ключевой строкой будет строка x4.
После преобразования, получим следующий опорный план:
|
Б.п.
|
1
|
–X4
|
–X3
|
|
X2 =
|
3
|
–2
|
1/2
|
|
X1 =
|
6
|
3
|
–1/2
|
|
X5 =
|
1
|
–4
|
1/2
|
|
Z =
|
66
|
5
|
1/2
|
Этот опорный план является оптимальным, т.к. в Z-строке все элементы положительны.
Этой таблице соответствует опорное решение.
(6;3;0;0;1)
Получаем, что максимальное значение Z=66 достигается при следующих значениях
переменных: X1=6;
X2=3.
б) Решим задачу графическим методом.
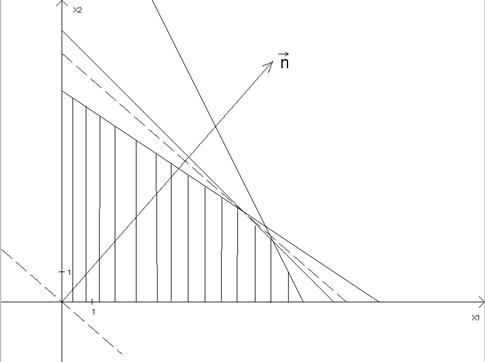
Область допустимых значений образует вертикально заштрихованный
многоугольник.
Строим нормаль линий уровня 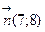
Построив опорные линии (на чертеже обозначены пунктиром),
получаем, что максимум целевой функции достигается в точке (6;3) и равен 66.
34. На трех базах A1, A2,
A3 имеется
однородный груз в количестве a1
т на базе A1,
a2 т на базе
A2, a3 т на базе A3. Полученный
груз требуется перевезти в пять пунктов: b1 т в пункт B1, b2
т в пункт B2,
b3 т в пункт
B3, b4 т в пункт B4, b5 т в пункт B5.
Затраты на перевозку грузов между пунктами поставок и
потребления заданы матрицей тарифов C:
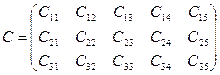 ,
,
где Cij
– стоимость перевозки 1 т груза от i-го поставщика j–му
потребителю в тыс. руб.
Спланировать перевозки так, чтобы их общая стоимость была
минимальной.
34. a1=150;
a2=150; a3=200; b1=100;
b2=70;
b3=130; b4=110; b5=90
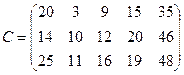
Т.к. 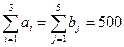 , то транспортная задача закрытая.
, то транспортная задача закрытая.
Запишем данные в виде матрицы перевозок.
|
Базы
|
Потребители
|
Запасы
|
|
B1
|
B2
|
B3
|
B4
|
B5
|
|
A1
|
20;
|
3;
|
9;
|
15;
|
35;
|
150;150
|
|
A2
|
14;
|
10;
|
12;
|
20;
|
46;
|
150;150
|
|
A3
|
25;
|
11;
|
16;
|
19;
|
48;
|
200;200
|
|
Потребности
|
100;100
|
70;70
|
130;130
|
110;110
|
90;90
|
500;500
|
После точки с запятой в каждой клетке будет стоять
количество грузов, которые необходимо перевести с i-ой базы j-му потребителю. В столбце «Запасы» и
строке «Потребности» после точки с запятой будут располагаться запасы и
потребности, оставшиеся нераспределенными.
Решать задачу будем по следующему принципу:
1. Ищем в матрице минимальный тариф из тех, которые еще не
используются, т.е. из клеток, в которых не стоит второго числа.
2. Вписываем туда максимально возможную поставку. Уменьшаем
соответственно потребности потребителя и запасы базы.
3. Если потребности потребителя стали равны 0 (потребности
данного потребителя удовлетворены полностью), то во все незаполненные клетки
столбца данного потребителя пишем 0. Если запасы базы стали равны 0 (запасы
данной базы иссякли полностью), то во все незаполненные клетки строки данной
базы пишем 0.
4. Если не все клетки заполнены, возвращаемся к п. 1.
В итоге получим следующее решение.
|
Базы
|
Потребители
|
Запасы
|
|
B1
|
B2
|
B3
|
B4
|
B5
|
|
A1
|
20;0
|
3;70
|
9;80
|
15;0
|
35;0
|
150;0
|
|
A2
|
14;100
|
10;0
|
12;50
|
20;0
|
46;0
|
150;0
|
|
A3
|
25;0
|
11;0
|
16;0
|
19;110
|
48;90
|
200;0
|
|
Потребности
|
100;0
|
70;0
|
130;0
|
110;0
|
90;0
|
500;0
|