План работы
Введение . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . 3
1. Статистическое изучение
производственных показателей организации на основе метода группировок (на
примере фондовооружённости и производительности труда) . . 4
1.1. Показатели фондовооружённости
и производительности труда . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.2. Понятие и виды группировок .
. . . . . . . . . . . . . . . . . . . . . . . . . 6
1.3. Принципы выбора
группировочного признака. Образование
групп и интервалов группировки . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . 14
2. Расчётная часть . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . 28
3. Аналитическая часть . . . . . .
. . . . . . . . . . . . . . . . . . . . . . 35
Заключение . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . 41
Список
использованной литературы . . . . . . .
. . . . . . . . . 42
Приложения . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . 43
Введение
Опираясь на диалектическое единство синтеза и
анализа как дополняющих друг друга способов познания, допуская определённую
степень абстракции, статистическое исследование производит расчленение
множества единиц изучаемой совокупности на различающиеся между собой, но
внутренне однородные части и одновременно с этим объединяет их в типичные
группы по существенному для них признаку.
Существование множества
форм развития экономических явлений, а также конкретных целей исследования и
неоднородных по содержанию исходных данных обусловливает необходимость
осуществления разнообразных приемов группировок.
В работе даётся понятие
группировки, рассматриваются отдельные их виды. Кроме того, рассматриваются
основные принципы выбора группировочного признака и интервалов.
Практическая часть
наглядно демонстрирует возможность применения метода группировки в
экономическом исследовании.
Работа выполнена с использованием пакета
прикладных программ MS Office XP.
Текстовая часть выполняется в Word, расчёты к расчётной и
аналитической частям – в Excel.
1. Статистическое изучение
производственных показателей организации на основе метода группировок (на примере
фондовооружённости и производительности труда)
1.1. Показатели фондовооружённости и производительности труда
Конечная эффективность использования основных
средств характеризуются показателями фондоотдачи, фондоёмкости,
фондовооружённости и относительной экономии основных средств.
Фондовооружённость – применяется для
характеристики оснащенности труда работников
(рабочих) основными средствами и показывает, сколько основных средств в
стоимостном выражении приходится на одного рабочего. Показатель фондовооруженности
может исчисляться как на определенную дату, в этом случае берут стоимость
основных средств и списочную численность на эту дату, так и в среднем за
период, тогда для расчетов применяют среднесписочную численность и
среднегодовую стоимость основных средств.
Формула для расчёта фондовооружённости (1):
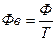 (1)
(1)
где Т –
численность работников (рабочих) среднесписочная или на определённую дату,
Ф – стоимость основных
средств среднегодовая или на определённую дату.
Под производительностью труда понимается результативность
конкретного живого труда, степень эффективности живого труда, его фактическая
способность производить в единицу времени определённое количество
потребительских ценностей или количество затраченного времени на производство
единицы продукции, эффективность целесообразной производительной деятельности
по созданию продукта в течение определённого промежутка времени.
Производительность труда (выработка) – отношение
произведённой или реализованной продукции (Q) к затратам труда на производство этой продукции (Т):
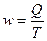 (2)
(2)
Показатель выработки отражает количество
продукции (в натуральном или стоимостном выражении), произведённой в единицу времени или одним
работником (рабочим). В качестве затрат труда могут выступать отработанные
человеко-часы, человеко-дни или численность работников (рабочих).
Фондовооружённость связана с показателями
фондоотдачи (Н) и производительности
труда следующей функциональной зависимостью:
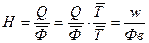 (3)
(3)
Из формулы видно, что рост фондоотдачи происходит
в результате опережающего роста производительности по сравнению с ростом фондовооружённости.
1.2. Понятие и виды группировок
Группировка – это процесс
образования однородных групп на основе расчленения статистической совокупности
на части или объединение изучаемых единиц в частные совокупности по
существенным для них признакам [1, стр. 53].
Группировка – это
распределение единиц по группам в соответствии со следующим принципом:
различия между единицами, отнесенными к одной группе, должны быть меньше, чем
между единицами, отнесенными к разным группам [2, стр. 118].
Группировка
производится с целью установления статистических связей и закономерностей,
построения описания объекта, выявления структуры изучаемой совокупности.
Различия в целевом назначении группировки выражаются в существующей в
отечественной статистике классификации группировок:
·
типологические,
·
структурные,
·
аналитические.
Типологическая
группировка служит
для выделения социально-экономических типов. Этот вид группировок в
значительной степени определяется представлениями экспертов о том, какие типы
могут встретиться в изучаемой совокупности.
Рассмотрим
последовательность действий для проведения этой группировки:
1) называются
те типы явлений, которые могут быть выделены;
2) выбираются
группировочные признаки, формирующие описание типов;
3) устанавливаются
границы интервалов;
4) группировка
оформляется в таблицу, выделенные группы (на основе комбинации группировочных
признаков) объединяются в намеченные типы, и определяется численность каждого
из них.
Многообразие
общественных явлений обусловливает необходимость дифференцированного подхода к
образованию и использованию типологических группировок.
Изменение границ
интервалов группировочного признака при выделении одних и тех же типов в разных
условиях называется специализацией интервалов группировочного признака. [2, стр. 123]
Иногда условия
формирования типов приводят к различиям в их описании, в самом круге признаков.
Изменение круга группировочных признаков при выделении одних и тех же типов в
разных условиях называется специализацией группировочных признаков. [2, стр. 123]
Предположим, что мы
располагаем данными 15 фирм, представляющих три подотрасли промышленности
(пример условный). Проведем их группировку с учётом подотасли, к которой
относятся предприятия и уровня производительности труда (табл. 1.1).
Таблица 1.1
Группировка акционерных компаний района
по уровню производительности труда
|
Подотрасль промышленности
|
Производительность труда, тыс. руб./час.
|
Тип
компании
|
Число компаний
|
|
Производство
детских игрушек
|
До 5
|
Н
|
-
|
|
5 – 10
|
С
|
1
|
|
10 и более
|
В
|
4
|
|
Производство
автомобильного масла
|
До 10
|
Н
|
1
|
|
10 – 20
|
С
|
2
|
|
20 и более
|
В
|
-
|
|
Производство
хлопчатобумажных тканей
|
До 10
|
Н
|
2
|
|
10 – 30
|
С
|
4
|
|
30 и более
|
В
|
1
|
В данном примере
выявлены три типа компаний: с низким уровнем производительности (Н), со средним
уровнем (С) и с высоким уровнем (В).
Результат группировки
компаний по уровню производительности представлен в табл. 1.2.
Таблица 1.2
Распределение акционерных компаний
района по уровню производительности труда
|
Тип компаний
|
Число компаний
|
|
абсолютное
|
в процентах к итогу
|
|
Н
|
3
|
20,0
|
|
С
|
7
|
46,7
|
|
В
|
5
|
33,3
|
|
Итого
|
15
|
100,0
|
Структурная группировка характеризует
структуру совокупности по какому-либо одному признаку (фондовооружённости или
производительности). Это группировки, используемые для изучения строения
изучаемой совокупности. В большинстве своем структурные группировки
производятся на основе образования качественно однородных групп, хотя нередко
они применяются и без предварительного расчленения совокупности на части.
Если для типологической группировки
чаще используются открытые и неравные интервалы, то для структурной группировки
более характерны закрытые равные интервалы [2, стр. 125]. Структурная группировка позволяет
изучать интенсивность вариации группировочного признака.
Структура совокупности
характеризуется относительной величиной структуры, которая рассчитывается как
отношение части совокупности к общему её объёму:
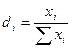 (4)
(4)
где 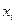 - уровень i – й части совокупности,
- уровень i – й части совокупности,
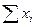 - суммарный уровень совокупности.
- суммарный уровень совокупности.
Пример структурной
группировки предприятий по производительности труда представлен в расчётной
части работы (задание 1).
Последовательность действий для проведения структурной
группировки:
1.
выбирается группировочный признак;
2.
устанавливаются границы интервалов;
3.
по каждой группе рассчитываются относительные величины
структуры;
4.
группировка оформляется в таблицу.
Аналитическая группировка используется для изучения
стохастической (вероятностной) взаимосвязи между взаимодействующими признаками.
Аналитическая группировка характеризует
взаимосвязь между двумя и более признаками, из которых один рассматривается как
результат, другой (другие) – как фактор (факторы). Например, можно изучать зависимость
производительности труда от фондовооружённости (задание 2 расчётной части
работы).
В экономике встречается
большое разнообразие взаимосвязей между признаками, выступающими в роли
причины или следствия явления. Из них можно выделить следующие:
1. когда
фактором выступает количественный признак, а результативным – качественный (уровень
производительности труда с одной стороны, и качеством выпущенной продукции – с
другой);
2. когда
в основу группировки положен качественный признак,
а результативным – представлен количественный (например, квалификация
работников и производительность их труда);
3. когда
в роли фактора и результата выступает качественный
признак (например, категории работников и их образование);
4. когда
в группировке факторный и результативный показатели представлены количественным
признаком (например, производительность труда и фондовооружённость).
Особенность аналитической группировки заключается в
том, что каждая группа характеризуется средним значением результативного
признака. Это позволяет выявить наличие и направление связи между
результативным и факторными признаками.
Для оценки
тесноты связи между результативным и факторным признаками рассчитывают
коэффициент детерминации и эмпирическое корреляционное отношение.
Коэффициент
детерминации определяется отношением межгрупповой дисперсии к общей
дисперсии (5):
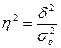 (5)
(5)
По значению
коэффициента можно судить, какая часть общей дисперсии результативного признака
обусловлена вариацией признака, положенного в основу группировки. Чем больше
значение этого показателя, тем теснее связь между результатом и фактором.
Общая дисперсия характеризует вариацию результативного признака,
которая зависит от всех условий, влияющих на совокупность. Она равна (6):
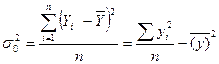 (6)
(6)
По правилу сложения дисперсий общая дисперсия определяется как сумма
межгрупповой дисперсии и средней из внутригрупповых дисперсий (7):
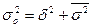 (7)
(7)
Межгрупповая дисперсия характеризует вариацию результативного признака
вызываемую фактором, положенным в основание группировки (8):

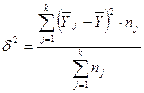 (8)
(8)
Средняя дисперсия из внутригрупповых дисперсий характеризует вариацию
результативного признака под воздействием факторов, не положенных в основу
группировки. Расчёт средней из внутригрупповых дисперсий осуществляется по
формуле (9):

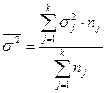 (9)
(9)
Эмпирическое
корреляционное соотношение рассчитывается как корень квадратный из коэффициента
детерминации (10) и характеризует тесноту связи между результативным и
факторным признаками:
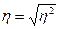 (10)
(10)
Направление связи между
результативным и факторным признаками наглядно видно из таблицы, в которой
представляются результаты группировки. Так, если с ростом факторного признака
от группы к группе растёт значение результативного признака, то говорят, что
связь прямая, если же с ростом факторного признака значение результата
сокращается, то связь обратная.
Пример аналитической
группировки и пример расчёта показателей тесноты связи представлен в расчётной
части работы (задание 2).
Сводные показатели для
отдельных групп являются типичными и устойчивыми, если:
во-первых группировка проведена правильно,
во-вторых группы имеют достаточную численность.
Первое условие связано
с тем, что деление на группы далеко не всегда очевидно. Выполнение второго
условия необходимо, так как при достаточно большом числе единиц (не менее 5
единиц в группе) в сводных показателях взаимопогашаются случайные характеристики
и проявляются закономерные, типичные.
Для решения задачи
группировки нужно установить правила отнесения каждой единицы к той или иной
группе.
В эти правила входят
определения тех характеристик (признаков), по которым будет проводиться
группировка (так называемых группировочных признаков), и их значений,
отделяющих одну группу от другой (интервалов группировки).
Группировка называется
простой (монотетической), если для ее построения используется один
группировочный признак. Если группировка проводится по нескольким признакам,
она называется сложной (политетической). Обычно такая группировка проводится
как комбинационная, т.е. группы, выделенные по одному признаку, подразделяются
на подгруппы по другому признаку. Казалось бы, этот метод выделения групп
должен быть лучше простой группировки -ведь трудно ожидать, что различия между
группами можно уловить лишь на основе одного признака. Однако комбинация
признаков приводит к дроблению совокупности в геометрической прогрессии: число
групп будет равно произведению числа группировочных признаков на число
выделенных категорий по каждому из них. Данные становятся труднообозримыми,
группы включают малое число единиц, групповые показатели становятся ненадежными.
Комбинированные группировки. Образование групп по двум
и более признакам, взятым в определенном сочетании, называется комбинированной
группировкой. При этом группировочные признаки принято располагать начиная с
атрибутивного, в определенной последовательности, исходя из логики взаимосвязи
показателей.
Применение комбинированных группировок
обусловлено многообразием экономических явлений, а также необходимостью их
всестороннего изучения. Но увеличение числа группировочных признаков
ограничивается уменьшением наглядности, что снижает эффективность использования
статистической информации. Пример комбинированной группировки представлен в
таблице 1.1. В данном случае, группировка предприятий осуществляется по двум
признакам: по подотрасли, к которой принадлежит предприятие и по уровню выплаты
дивидендов.
Процесс образования
новых групп на основе группировки, произведенной по первичным данным,
называется вторичной группировкой. Необходимость во вторичной
группировке возникает в случаях:
- когда в результате первоначальной
группировки нечетко проявился характер распределения изучаемой совокупности (в
этом случае производят укрупнение или уменьшение интервалов);
- когда требуется свести воедино или
сопоставить между собой данные, полученные в результате применения различных
приемов группировки.
Вторичная группировка может быть
осуществлена по признаку, положенному в основу первичной группировки, или по
удельному весу групп в общей численности единиц совокупности, подвергнутой
первичной группировке. При этом в обоих случаях показатели новых групп, т.е.
групп, образованных при вторичной группировке, могут быть получены путем
простого суммирования показателей первичной группировки или в результате
специальных расчетов.
1.3. Принципы выбора группировочного признака. Образование групп и интервалов группировки
Экономические явления
отличаются большим многообразием форм своего развития, и поэтому при
группировке встает вопрос о выборе того признака, который адекватен цели
исследования и характеру исходной информации. Руководствуясь теоретическими
положениями экономической науки и исходя из задач исследования, для
осуществления группировки необходимо из множества признаков выбрать
определяющие.
Определяющими являются
признаки, которые наиболее полно и точно характеризуют изучаемый объект,
позволяют выбрать его типичные черты и свойства. Например, любое коммерческое
предприятие характеризуется различными признаками, каждый из которых имеет
определённое значение. Тем не менее, основным и существенным признаком
величины предприятия является объём производства, свидетельствующий о масштабах
организации.
Важным моментом при выборе группировочного
признака является необходимость учёта изменившихся обстоятельств, в которых
действует то или иное явление. Принцип соблюдения условия места и времени
здесь должен выполняться.
Все многообразие
признаков, на основе которых могут производиться статистические группировки,
можно классифицировать.
1. По форме выражения
группировочные признаки могут быть атрибутивными, не имеющими количественного
значения (профессия, образование и т.д.), и количественными, т.е. признаками, принимающими
различные цифровые характеристики у отдельных единиц изучаемой совокупности
(число работающих, выпуск продукции и т.д.). При этом количественные признаки,
в свою очередь, могут быть дискретными (прерывными), значения которых
выражаются только целыми числами (число цехов и т.д.), и непрерывными,
принимающими как целые, так и дробные значения (объем выпуска в стоимостном
выражении, уровень производительности труда).
2. По характеру
колеблемости группировочные признаки могут быть альтернативными, которыми одни
единицы обладают, а другие - нет (например, основные средства – в эксплуатации
или на консервации), и имеющими множество количественных значений (например,
размер производственной площади, величина фонда оплаты труда и т.д.).
3. По той роли, которую
играют признаки во взаимосвязи изучаемых явлений, их подразделяют на факторные, воздействующие на другие
признаки, и результативные, испытывающие
на себе влияние других. Причем в зависимости от сложившихся объективных условий
и цели исследования признаки могут меняться ролями. В одних случаях они
являются факторными признаками, в других - результативными. Так, с одной
стороны, производительности труда зависит от качества подготовки и деятельности
работников, с другой – является основным
источником роста объёма производства, а, следовательно, и масштабов всего
предприятия (основных фондов, увеличения числа работников торговли и т.д.).
Таким образом, в первом случае производительность выступает результативным
признаком, во втором - факторным. А это положение имеет важное значение в
статистическом исследовании.
Следующим важным шагом
после определения группировочного признака является распределение единиц
совокупности по группам. Здесь встаёт вопрос о количестве групп и величине интервала,
которые между собой взаимосвязаны. При прочих равных условиях чем больше число
групп, тем меньше величина интервала, и наоборот. Одним из основных
требований, возникающих при решении данного вопроса, является выбор такого
числа групп и величины интервала, которые позволяют более равномерно
распределить единицы совокупности по группам и достичь при этом их
представительности, качественной однородности. Оптимальная наполняемость
интервалов является важным критерием правильности группировки.
Вопрос о числе групп и
величине интервала следует решать с учетом множества обстоятельств, прежде
всего исходя из целей исследования, значения изучаемого признака, всего
процесса коммерческой деятельности и т.д.
Количество групп во
многом зависит от того, какой признак служит основанием группировки. Так,
нередко атрибутивные группировочные признаки предопределяют число групп. По
аналогии также расчленяется совокупность по дискретному признаку,
изменяющемуся в незначительном диапазоне.
Интервалы групп устанавливаются только при
значительной колеблемости дискретного признака (число работников) и тем более
при непрерывно изменяющемся количественном признаке.
Число групп тесно
связано с объемом совокупности. Здесь нет строго научных приемов, позволяющих
решать этот вопрос при любых взаимосвязях названных величин. Всякий раз эта
задача решается с учетом конкретных обстоятельств.
Однако при равенстве
интервалов для ориентировки существует формула, предложенная американским
ученым Стерджессом, с помощью которой можно наметить число групп n при известной численности совокупности N:
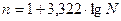 (11)
(11)
Эта формула показывает,
что число групп – функция объема данных.
Зная размах колеблемости
значений изучаемого признака во всей совокупности и намечаемое число групп,
величина равного интервала определяется
по формуле
Закрытые интервалы
подразделяются на равные и неравные. Величина равного интервала
находится по формуле (12):
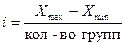 (12)
(12)
В экономической практике в большинстве своем
применяются неравные интервалы, прогрессивно возрастающие или убывающие.
Такая необходимость возникает особенно в тех случаях, когда колеблемость признака
осуществляется неравномерно и в больших пределах.
Неравные интервалы
могут определяться как равнонаполненные.
При этом совокупность разделяется на группы равного объема с числом
единиц в каждой группе (13):
n = N : m (13)
где N - общее число единиц;
n - число
групп.
Данные ранжируются,
отсчитывается число единиц, составляющих первую группу, затем – вторую и т.д.
Границы интервалов
будут соответствовать фактическим значениям признака в каждой группе.
Бывает, что число групп
заранее неизвестно и определяется опытным путем на основе перебора вариантов
группировки, выявления такого варианта, который наилучшим образом позволяет
увидеть различия между группами.
При определении числа
групп следует обращать внимание на то, чтобы в одну группу не попало бы свыше
половины всех единиц совокупности и в средних группах было больше единиц, чем в
крайних.
В пределах одной
группировки могут применяться несколько признаков и устанавливаться разной
величины интервалы.
Аналогично поступают и
в том случае, когда на основе мелких групп образуют более крупные (удлиняя
интервалы), позволяющие получить новое качество групп, не нарушая их
однородности.
Используются интервалы открытые и закрытые. В
первом случае указываются верхняя и
нижняя границы интервала. Такая
запись предполагает, что единица, у которой значение признака совпадает с
верхней границей интервала, относится к следующей группе, т.е. интервал
читается как «от - до».
Иногда границы закрытых
интервалов предполагают включение единиц с нижней и верхней границами. Интервал
называется открытым, если указана либо только верхняя.
Если группировочный
признак неколичественный, или количественный дискретный с малым числом
значений, то группировка данных производится путем подсчета числа единиц с
данным значением признака.
2. Расчётная часть
Задание 1
По
исходным данным табл. 2.1:
1.
Постройте статистический ряд распределения организаций по признаку уровень
производительности труда образовав пять групп с равными интервалами.
2.
Постройте графики полученного ряда распределения.
Графически определите значения моды и медианы.
3.
Рассчитайте характеристики ряда распределения: среднюю
арифметическую, среднее квадратическое отклонение, коэффициент вариации.
4.
Вычислите среднюю арифметическую по исходным данным
(табл. 1), сравните её с аналогичным показателем, рассчитанным в п. 3
настоящего задания. Объясните причину их расхождения.
Сделайте
выводы по результатам выполнения задания.
Таблица 2.1
|
№
организации
|
Объём продукции, млн. руб.
|
Среднесписочная
численность работников, чел.
|
Производительность
труда, тыс. руб./чел.
|
|
1
|
36,450
|
162
|
225
|
|
2
|
23,400
|
156
|
150
|
|
3
|
46,540
|
179
|
260
|
|
4
|
59,752
|
194
|
308
|
|
5
|
41,415
|
165
|
251
|
|
6
|
26,860
|
158
|
170
|
|
7
|
79,200
|
220
|
360
|
|
8
|
54,720
|
190
|
288
|
|
9
|
40,424
|
163
|
248
|
|
10
|
30,210
|
159
|
190
|
|
11
|
42,418
|
167
|
254
|
|
12
|
64,575
|
205
|
315
|
|
13
|
51,612
|
187
|
276
|
|
14
|
35,420
|
161
|
220
|
|
15
|
14,400
|
120
|
120
|
|
16
|
36,936
|
162
|
228
|
|
17
|
53,392
|
188
|
284
|
|
18
|
41,000
|
164
|
250
|
|
19
|
55,680
|
192
|
290
|
|
20
|
18,200
|
130
|
140
|
|
21
|
31,800
|
159
|
200
|
|
22
|
39,204
|
162
|
242
|
|
23
|
57,128
|
193
|
296
|
|
24
|
28,440
|
158
|
180
|
|
25
|
43,344
|
168
|
258
|
|
26
|
70,820
|
208
|
340
|
|
27
|
41,832
|
166
|
252
|
|
28
|
69,345
|
207
|
335
|
|
29
|
35,903
|
161
|
223
|
|
30
|
50,220
|
186
|
270
|
Решение:
Вариационный ряд – упорядоченное распределения единиц совокупности чаще
по возрастающим или по убывающим (реже) значениям признака и подсчет числа
единиц с тем или иным значением признака.
Различают
следующие формы вариационного ряда:
Ранжированный ряд — это перечень отдельных единиц совокупности в
порядке возрастания (убывания) изучаемого признака.
Если
признак принимает небольшое число значений, строится дискретный вариационный
ряд. Дискретный вариационный ряд — это таблица, состоящая из двух строк или
граф: конкретных значений варьирующего признака.
Число
групп в дискретном вариационном ряду определяется числом реально существующих
значений варьирующего признака.
Если
признак может принимать хотя и дискретные значения, но их число очень велико,
тогда строится интервальный вариационный ряд. Интервальный вариационный
ряд строится и для изучения признаков, которые могут принимать любые, как
целые, так и дробные, значения в области своего существования.
Интервальный
вариационный ряд представляет собой таблицу, состоящую из двух граф (или строк)
— интервалов признака, вариация которого изучается, и числа единиц
совокупности, попадающих в данный интервал (частот), или долей этого числа от
общей численности совокупности (частостей).
При
построении интервального вариационного ряда необходимо выбрать оптимальное
число групп (интервалов признака) и установить длину интервала.
1.
Построим интервальный вариационный ряд с 5 равными интервалами, для
этого построим ранжированный ряд предприятий по производительности труда в
порядке возрастания. Результаты представлены в таблице 2.2.
Таблица 2.2
|
№
организации
|
Объём продукции
|
Среднесписочная
численность работников, чел.
|
Производительность
труда, тыс. руб./чел.
|
|
15
|
14,400
|
120,000
|
120
|
|
20
|
18,200
|
130,000
|
140
|
|
2
|
23,400
|
156,000
|
150
|
|
6
|
26,860
|
158,000
|
170
|
|
24
|
28,440
|
158,000
|
180
|
|
10
|
30,210
|
159,000
|
190
|
|
21
|
31,800
|
159,000
|
200
|
|
14
|
35,420
|
161,000
|
220
|
|
29
|
35,903
|
161,000
|
223
|
|
1
|
36,450
|
162,000
|
225
|
|
16
|
36,936
|
162,000
|
228
|
|
22
|
39,204
|
162,000
|
242
|
|
9
|
40,424
|
163,000
|
248
|
|
18
|
41,000
|
164,000
|
250
|
|
5
|
41,415
|
165,000
|
251
|
|
27
|
41,832
|
166,000
|
252
|
|
11
|
42,418
|
167,000
|
254
|
|
25
|
43,344
|
168,000
|
258
|
|
3
|
46,540
|
179,000
|
260
|
|
30
|
50,220
|
186,000
|
270
|
|
13
|
51,612
|
187,000
|
276
|
|
17
|
53,392
|
188,000
|
284
|
|
8
|
54,720
|
190,000
|
288
|
|
19
|
55,680
|
192,000
|
290
|
|
23
|
57,128
|
193,000
|
296
|
|
4
|
59,752
|
194,000
|
308
|
|
12
|
64,575
|
205,000
|
315
|
|
28
|
69,345
|
207,000
|
335
|
|
26
|
70,820
|
208,000
|
340
|
|
7
|
79,200
|
220,000
|
360
|
|
Итого
|
|
|
7423
|
В
случае если интервалы равные, то их величина определяется по формуле (12):
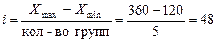 тыс. руб./чел.
тыс. руб./чел.
Xmax и Х min - соответственно максимальная и минимальная
величина производительности труда.
Получаем
следующие интервалы производительности труда, тыс. руб./чел.:
|
Нижняя граница
|
Верхняя граница
|
|
120
|
168
|
|
168
|
216
|
|
216
|
264
|
|
264
|
312
|
|
312
|
360
|
На
основе полученных данных составим ряд распределения табл. 2.3:
Таблица 2.3
Распределение предприятий по производительности труда
|
Группы
предприятий
по производительности труда, тыс. руб./чел.
|
Число
предприятий
|
|
В группе
|
В % к итогу
|
|
120
|
168
|
3
|
10,00%
|
|
168
|
216
|
4
|
13,33%
|
|
216
|
264
|
12
|
40,00%
|
|
264
|
312
|
7
|
23,33%
|
|
312
|
360
|
4
|
13,33%
|
|
Итого:
|
30
|
100,00%
|
Из
таблицы видно, что распределение предприятий по уровню производительности труда
отличается от нормального. Для нормального распределения характерно равенство
числа единиц попавших в первую и последнюю, вторую и предпоследнюю группы, чего
не наблюдается в данном случае.
2.
Графики ряда распределения.
Построим
гистограмму ряда распределения, для этого в прямоугольной системе координат по
оси абсцисс будем откладывать интервалы производительности труда, а по оси
ординат – число предприятий, принадлежащих к той или иной группе:
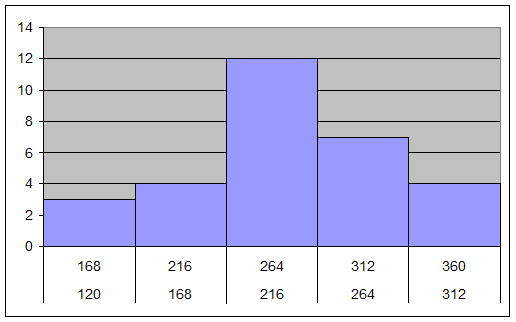
Рисунок 1. Гистограмма распределения
предприятий по уровню производительности труда
Мода
– это наиболее часто встречающееся значение признака в совокупности (в данном
случае – наиболее часто встречающийся размер уровень производительности труда).
Значение моды в ряду распределения определяется как значение признака, имеющего
наибольшую частоту.
В
нашем примере мода находится в интервале от 216
тыс. руб./чел. до 264 тыс. руб./чел., т. е. в данной совокупности
наиболее часто встречались предприятия с таким уровнем производительности
труда.
Медиана
– значение признака, которое делит совокупность на 2 равные части, это
значение, стоящее в середине ранжированного ряда. Графически медиана
определяется по кумуляте. Из точки на оси ординат, которая соответствует
половине накопленной частоты (15) восстанавливается перпендикуляр до
пересечения с кумулятой. Из точки пересечения восстанавливаем перпендикуляр на
ось абсцисс – данная точка и будет являться медианой. Кумулята – кривая сумм
накопленных частой, нижней границе первого интервала, которой соответствует
ноль, а верхней границе последнего интервала – вся накопленная частота, которая
равна численности совокупности.
Построим
кумуляту по следующим данным (табл. 2.4):
Таблица 2.4
|
Группы
предприятий
по производительности
труда, тыс.
руб./чел.
|
Накопленная частота
|
|
120
|
168
|
3
|
|
168
|
216
|
7
|
|
216
|
264
|
19
|
|
264
|
312
|
26
|
|
312
|
360
|
30
|
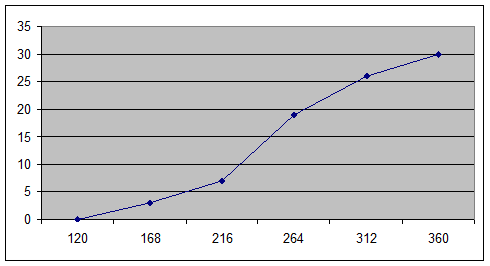
Рисунок 2. Кумулята распределения
предприятий по уровню производительности труда
Из
графика видно, что 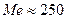 тыс. руб./чел., это
значит, что на 50% предприятий в отчётном году уровень производительности труда
был больше, чем 250 тыс. руб./чел., а на 50% предприятий – меньше этого
значения.
тыс. руб./чел., это
значит, что на 50% предприятий в отчётном году уровень производительности труда
был больше, чем 250 тыс. руб./чел., а на 50% предприятий – меньше этого
значения.
3.
Рассчитаем основные характеристики ряда распределения.
Для
расчёта основных характеристик построим рабочую таблицу 2.5. Перейдём от
интервального ряда к дискретному, заменив интервальные значения их средними
значениями (простая средняя между нижней и верхней границами интервала).
Таблица 2.5
|
Группы предприятий
по производительности труда, тыс. руб./чел.
|
Число
предприятий
|
Середина
интервала
|
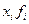
|
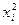
|
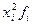
|
|
120
|
168
|
3
|
144
|
432
|
20736
|
62208
|
|
168
|
216
|
4
|
192
|
768
|
36864
|
147456
|
|
216
|
264
|
12
|
240
|
2880
|
57600
|
691200
|
|
264
|
312
|
7
|
288
|
2016
|
82944
|
580608
|
|
312
|
360
|
4
|
336
|
1344
|
112896
|
451584
|
|
|
|
30
|
Х
|
7440
|
X
|
1933056
|
Найдём
среднюю арифметическую:
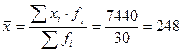 (тыс. руб./чел.) –
уровень производительности труда на каждом предприятии за отчётный год составил
в среднем 248 тыс. руб./чел.
(тыс. руб./чел.) –
уровень производительности труда на каждом предприятии за отчётный год составил
в среднем 248 тыс. руб./чел.
Дисперсия
признака – это средний квадрат отклонений вариантов от их средней величины:
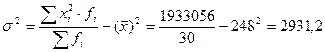
Среднее
квадратическое отклонение показывает на
сколько в среднем отклоняются конкретные варианты от их среднего значения и
численно равно корню квадратному из дисперсии:
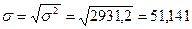 (тыс. руб./чел.)
(тыс. руб./чел.)
Коэффициент вариации:
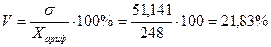
Значение
коэффициента меньше 40%, следовательно, вариация производительности в данной
совокупности незначительна, а совокупность однородна.
4.
Рассчитаем среднее значение производительности по исходным данным по
формуле средней арифметической простой:
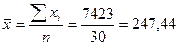 (млн. руб.)
(млн. руб.)
Полученное
значение отличается от значения в п. 3 т. к. в п. 3 вычисления происходили по
сгруппированным данным, причём, для расчётов брались приближённые значения
вариант (середины интервалов).
Задание 2
По
исходным данным табл. 2.6:
1.
Установите наличие и характер связи между признаками фондовооружённость труда
и уровень производительности труда образовав пять групп с равными интервалами
по обоим признакам, методами:
а)
аналитической группировки,
б)
корреляционной таблицы.
2.
Измерьте тесноту корреляционной связи между названными признаками с
использованием коэффициента детерминации и эмпирического корреляционного отношения.
Сделайте
выводы.
Таблица 2.6
|
№
организации
|
Среднесписочная
численность работников, чел.
|
Производительность
труда, тыс. руб./чел.
|
Среднегодовая
стоимость основных производственных фондов, млн. руб.
|
Фондовооружённость,
тыс. руб./чел.
|
|
1
|
162
|
225
|
34,714
|
214,28
|
|
2
|
156
|
150
|
24,375
|
156,25
|
|
3
|
179
|
260
|
41,554
|
232,15
|
|
4
|
194
|
308
|
50,212
|
258,82
|
|
5
|
165
|
251
|
38,347
|
232,41
|
|
6
|
158
|
170
|
27,408
|
173,47
|
|
7
|
220
|
360
|
60,923
|
276,92
|
|
8
|
190
|
288
|
47,172
|
248,27
|
|
9
|
163
|
248
|
37,957
|
232,87
|
|
10
|
159
|
190
|
30,210
|
190,00
|
|
11
|
167
|
254
|
38,562
|
230,91
|
|
12
|
205
|
315
|
52,500
|
256,10
|
|
13
|
187
|
276
|
45,674
|
244,25
|
|
14
|
161
|
220
|
34,388
|
213,59
|
|
15
|
120
|
120
|
16,000
|
133,33
|
|
16
|
162
|
228
|
34,845
|
215,09
|
|
17
|
188
|
284
|
46,428
|
246,96
|
|
18
|
164
|
250
|
38,318
|
233,65
|
|
19
|
192
|
290
|
47,590
|
247,86
|
|
20
|
130
|
140
|
19,362
|
148,94
|
|
21
|
159
|
200
|
31,176
|
196,08
|
|
22
|
162
|
242
|
36,985
|
228,30
|
|
23
|
193
|
296
|
48,414
|
250,85
|
|
24
|
158
|
180
|
28,727
|
181,82
|
|
25
|
168
|
258
|
39,404
|
234,55
|
|
26
|
208
|
340
|
55,250
|
265,63
|
|
27
|
166
|
252
|
38,378
|
231,19
|
|
28
|
207
|
335
|
55,476
|
268,00
|
|
29
|
161
|
223
|
34,522
|
214,42
|
|
30
|
186
|
270
|
44,839
|
241,07
|
Решение:
Построим
аналитическую группировку предприятий по уровню фондовооружённости труда.
Факторным признаком в данном случае будет являться фондовооружённость, а
результативным – уровень производительности труда.
Построим
макет итоговой таблицы.
|
Группы предприятий
по фондовооружённости труда, тыс. руб./чел
|
Число
предприятий
|
Производительность
труда, тыс. руб./чел.
|
|
Всего
|
В среднем
на 1 предприятие
|
|
|
|
|
|
|
|
|
|
|
|
Итого
|
|
|
|
Ранжируем
исходные данные в порядке возрастания фондовооружённости. Результаты расчётов
для построения аналитической группировки представим в таблице 2.7.
Таблица 2.7
|
№
|
Фондовооружённость,
тыс. руб./чел.
|
Итого
|
Производительность
труда, тыс. руб./чел.
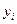
|
Итого
|
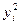
|
Дисперсия
|
|
15
|
133,33
|
|
120
|
|
14400
|
|
|
20
|
148,94
|
|
140
|
|
19600
|
|
|
2
|
156,25
|
438,521795
|
150
|
410
|
22500
|
155,5556
|
|
6
|
173,47
|
|
170
|
|
28900
|
|
|
24
|
181,82
|
|
180
|
|
32400
|
|
|
10
|
190,00
|
545,28
|
190
|
540
|
36100
|
66,6667
|
|
21
|
196,08
|
|
200
|
|
40000
|
|
|
14
|
213,59
|
|
220
|
|
48400
|
|
|
1
|
214,28
|
|
225
|
|
50625
|
|
|
29
|
214,42
|
|
223
|
|
49729
|
|
|
16
|
215,09
|
1053,46
|
228
|
1096
|
51984
|
98,9600
|
|
22
|
228,30
|
|
242
|
|
58564
|
|
|
11
|
230,91
|
|
254
|
|
64516
|
|
|
27
|
231,19
|
|
252
|
|
63504
|
|
|
3
|
232,15
|
|
260
|
|
67600
|
|
|
5
|
232,41
|
|
251
|
|
63001
|
|
|
9
|
232,87
|
|
248
|
|
61504
|
|
|
18
|
233,65
|
|
250
|
|
62500
|
|
|
25
|
234,55
|
|
258
|
|
66564
|
|
|
30
|
241,07
|
|
270
|
|
72900
|
|
|
13
|
244,25
|
|
276
|
|
76176
|
|
|
17
|
246,96
|
|
284
|
|
80656
|
|
|
19
|
247,86
|
2836,15
|
290
|
3135
|
84100
|
213,8542
|
|
8
|
248,27
|
|
288
|
|
82944
|
|
|
23
|
250,85
|
|
296
|
|
87616
|
|
|
12
|
256,10
|
|
315
|
|
99225
|
|
|
4
|
258,82
|
|
308
|
|
94864
|
|
|
26
|
265,63
|
|
340,4807692
|
|
115927,1542
|
|
|
28
|
268,00
|
|
335
|
|
112225
|
|
|
7
|
276,92
|
1824,59
|
360
|
2242,480769
|
129600
|
573,2261
|
|
|
|
6698,01813
|
|
7423,480769
|
1938624,154
|
3389,6199
|
Величина
интервала:
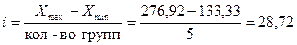 тыс. руб./чел.
тыс. руб./чел.
Xmax и Х min - соответственно максимальная и минимальная фондовооружённость
труда.
Получаем
следующие интервалы фондовооружённости, тыс. руб./чел:
|
Нижняя граница
|
Верхняя граница
|
|
133,33
|
162,05
|
|
162,05
|
190,77
|
|
190,77
|
219,49
|
|
219,49
|
248,20
|
|
248,20
|
276,92
|
Результаты
группировки представим в таблице 2.8.
Таблица 2.8
Группировка
предприятий по фондовооружённости
|
Группы предприятий
по фондовооружённости труда, тыс. руб./чел.
|
Число
предприятий
|
Производительность
труда, тыс. руб./чел.
|
|
Всего
|
В среднем
на 1 предприятие
|
|
133,33
|
162,05
|
3
|
410
|
136,67
|
|
162,05
|
190,77
|
3
|
540
|
180,00
|
|
190,77
|
219,49
|
5
|
1096
|
219,20
|
|
219,49
|
248,20
|
12
|
3135
|
261,25
|
|
248,20
|
276,92
|
7
|
2242
|
320,35
|
|
Итого
|
30
|
7423
|
247,45
|
Из
таблицы видно, что между фондовооружённостью и уровнем производительности труда существует
прямая корреляционная связь. С ростом фондовооружённости от группы к группе
растёт средний уровень производительности на каждое предприятие.
Для
оценки тесноты этой связи рассчитаем коэффициент детерминации и эмпирическое
корреляционное отношение.
Общая дисперсия характеризует вариацию
результативного признака, которая зависит от всех условий, влияющих на
совокупность. В данном случае она характеризует вариацию производительности
труда под воздействием всех факторов в данной совокупности.
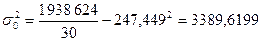
Рассчитаем среднюю из внутригрупповых дисперсий. В
данном случае эта дисперсия характеризует вариацию производительности труда за
счёт факторов, не положенных в основу группировку:

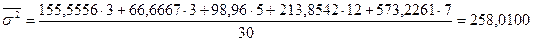
Рассчитаем межгрупповую дисперсию. Межгрупповая
дисперсия характеризует вариацию результативного признака, вызываемую фактором,
положенным в основание группировки. В данном случае она характеризует вариацию производительности
под влиянием изменения фондовооружённости:
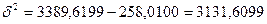
Коэффициент
детерминации определяется по формуле:
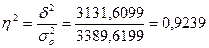
Расчёты
показали, что вариация производительности на 92,39% обусловлена вариацией фондовооружённости
труда.
Эмпирическое корреляционное отношение
рассчитывается как корень квадратный из коэффициента детерминации и
характеризует тесноту связи между результативным и факторным признаками:
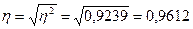
Таким
образом, между производительностью и фондовооружённостью труда существует
достаточно тесная прямая корреляционная связь.
Проверим
значимость коэффициента детерминации с помощью F-критерия Фишера:
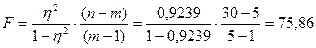
При
уровне значимости 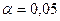 , числе степеней свободы
, числе степеней свободы 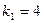 и
и 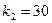 табличная величина F = 2,69 [1, стр.
434], поэтому значение коэффициента детерминации признаётся существенным.
табличная величина F = 2,69 [1, стр.
434], поэтому значение коэффициента детерминации признаётся существенным.
Построим
корреляционную таблицу (табл. 2.9).
Таблица 2.9
|
Группы предприятий
по производительности, тыс. руб.
|
Группы предприятий
по фондовооружённости труда,
тыс. руб./чел.
|
Итого
|
|
133,33-162,05
|
162,05-190,77
|
190,77-219,49
|
219,49-248,20
|
248,20-276,92
|
|
120-168
|
3
|
|
|
|
|
3
|
|
168-216
|
|
3
|
1
|
|
|
4
|
|
216-264
|
|
|
4
|
8
|
|
12
|
|
264-312
|
|
|
|
4
|
3
|
7
|
|
312-360
|
|
|
|
|
4
|
4
|
|
Итого
|
3
|
3
|
5
|
12
|
7
|
30
|
Как видно из данных таблицы 2.9, распределение
числа предприятий произошло вдоль диагонали, проведенной из левого верхнего
угла в правый нижний угол, т.е., увеличение фондовооружённости сопровождалось
ростом производительности труда.
Характер распределения частот по
диагонали корреляционной таблицы свидетельствует о наличии прямой корреляционной
связи между изучаемыми признаками.
Задание 3
По
результатам выполнения задания 1 с вероятностью 0,683 определите:
1.
Ошибку выборки среднего уровня производительности
труда и границы, в которых будет находиться производительность труда в
генеральной совокупности.
2.
Ошибку выборки доли организаций с уровнем
производительности 264 тыс. руб. и более и границы, в которых будет находиться
генеральная доля.
Решение:
1. Найдём среднюю ошибку механической
выборки, которая показывает, какие возможны отклонения между характеристиками
генеральной и выборочной совокупностей, по формуле собственно-случайной
бесповторной выборки:
Дано:
Доверительная вероятность 0,683; t=1 (коэффициент кратности при
доверительной вероятности 0,683).
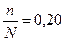 - процент выборки
- процент выборки
Величина возможной случайной ошибки репрезентативности характеризуется средней ошибкой
выборки. Она показывает, какие возможны отклонения между характеристиками
генеральной и выборочной совокупностей, и при бесповторном отборе, как в данном
случае, находится по формуле:
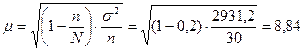 тыс. руб./чел.
тыс. руб./чел.
Найдем
предельное отклонение. Оно равно произведению коэффициента кратности t средней ошибки (показывает, сколько средних ошибок
находится в предельной ошибке с заданной вероятностью) на величину средней
ошибки. В данном случае:
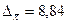 (тыс. руб./чел)
(тыс. руб./чел)
Найдем
предельную ошибку выборки, то есть, в каких пределах находится средняя сумма
прибыли отрасли в генеральной совокупности:
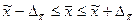
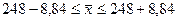
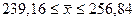
С
вероятностью 0,683 можно утверждать, что средняя производительность в
генеральной совокупности будет находиться в пределах от 239,16 до 256,84 тыс.
руб./чел.
2.
Выборочная доля определяется отношением числа единиц, обладающих изучаемым
признаком, к общему числу единиц выборочной совокупности:
n – общее число предприятий
выборочной совокупности (30):
m – число предприятий с уровнем
производительности 264 тыс. руб./чел. и более.
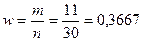
Найдём
среднюю ошибку выборки для доли, которая показывает, какие возможны отклонения
между характеристиками генеральной и выборочной совокупностей, по формуле
собственно-случайной бесповторной выборки:
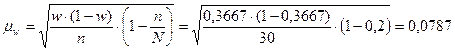
предельное
отклонение для заданной доверительной вероятности равно средней ошибке.
Найдем
в каких пределах находится генеральная доля:
Р-
генеральная доля совокупности ;
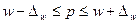
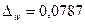
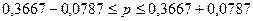
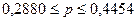
Значит
с вероятностью 0,683 можно утверждать, что генеральная доля предприятий с
уровнем производительности 264 тыс. руб. и более будет находиться в пределах от
0,288 до 0,4454 (от 28,8% до 44,54%).
Задание 4
Имеются
следующие данные по двум предприятиям отрасли:
|
Предприятие
|
Выпуск
продукции, тыс. руб.
|
Среднесписочная
численность рабочих, чел.
|
|
Базисный
период
|
Отчетный
период
|
Базисный
период
|
Отчетный
период
|
|
№1
|
6400
|
6000
|
100
|
80
|
|
№2
|
4800
|
6000
|
60
|
60
|
Определите:
1. По каждому предприятию уровни и динамику
производительности труда.
Результаты
расчетов представьте в таблице.
2. По двум предприятиям вместе:
-
индексы производительности труда (переменного, постоянного
состава, структурных сдвигов);
-
абсолютное изменение средней производительности труда
за счет отдельных факторов.
Решение:
1.
Найдём уровни производительности труда по каждому предприятию как отношение
объёма выпуска к численности работников.
Динамика
производительности характеризуется индексом:
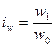
Результаты
расчётов представим в таблице 2.10.
Таблица 2.10
|
Предприятие
|
Производительность
труда, тыс. руб./чел.
|
Индекс
производительности
|
|
Базисный
период
|
Отчетный
период
|
|
№1
|
64
|
75
|
1,1719
|
|
№2
|
80
|
100
|
1,25
|
Определим
уровни производительности.
Базисный
период:
Предприятие
№1:
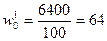 (тыс. руб./чел.) –
каждый работник предприятия №1 в базисном периоде произвёл продукции в среднем
на 64 тыс. руб.
(тыс. руб./чел.) –
каждый работник предприятия №1 в базисном периоде произвёл продукции в среднем
на 64 тыс. руб.
Предприятие
№2:
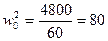 (тыс. руб./чел.) –
каждый работник предприятия №2 в базисном периоде произвёл продукции в среднем
на 80 тыс. руб.
(тыс. руб./чел.) –
каждый работник предприятия №2 в базисном периоде произвёл продукции в среднем
на 80 тыс. руб.
Рассчитаем
индексы динамики производительности.
Отчётный
период:
Предприятие
№1:
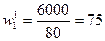 (тыс. руб./чел.) –
каждый работник предприятия №1 в отчётном периоде произвёл продукции в среднем
на 75 тыс. руб.
(тыс. руб./чел.) –
каждый работник предприятия №1 в отчётном периоде произвёл продукции в среднем
на 75 тыс. руб.
Предприятие
№2:
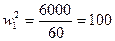 (тыс. руб./чел.) –
каждый работник предприятия №2 в отчётном периоде произвёл продукции в среднем
на 100 тыс. руб.
(тыс. руб./чел.) –
каждый работник предприятия №2 в отчётном периоде произвёл продукции в среднем
на 100 тыс. руб.
Предприятие
№1:
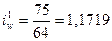 - производительность
труда на первом предприятии увеличилась в отчётном периоде на 17,19% по
сравнению с уровнем базисного периода.
- производительность
труда на первом предприятии увеличилась в отчётном периоде на 17,19% по
сравнению с уровнем базисного периода.
Предприятие
№2:
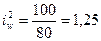 - производительность
труда на втором предприятии увеличилась в отчётном периоде на 25% по сравнению
с уровнем базисного периода.
- производительность
труда на втором предприятии увеличилась в отчётном периоде на 25% по сравнению
с уровнем базисного периода.
2.
Для анализа динамики средней производительности под влиянием ряда факторов
используется система индексов средних величин.
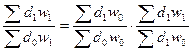
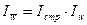
В
качестве факторов, влияющих на среднюю производительность, выступают структура
численности и производительность по каждому предприятию.
Результаты
вспомогательных расчётов представим в таблице 2.11.
Таблица 2.11
|
Предприятия
|
Производительность
труда, тыс. руб./чел.
|
Среднесписочная
численность
рабочих, чел.
|
Структура
производства
|
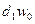
|
|
Базисный
период
w0
|
Отчетный
период w1
|
Базисный
период
d0
|
Отчетный
период
d1
|
Базисный
период
|
Отчетный
период
|
|
1
|
64
|
75
|
100
|
80
|
0,6250
|
0,5714
|
36,57
|
|
2
|
80
|
100
|
60
|
60
|
0,3750
|
0,4286
|
34,29
|
|
Итого
|
70
|
85,71
|
160
|
140
|
1
|
1
|
70,86
|
Рассчитаем индексы, входящие в систему.
Индекс динамики средней производительности
характеризует динамику средней производительности под влиянием двух факторов
(структуры численности и производительности по отдельным предприятиям):
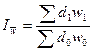
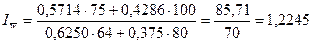
Разность между числителем и знаменателем индекса
(метод цепных подстановок) характеризует общее изменение средней производительности
в абсолютном выражении:
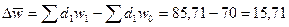 (тыс. руб./чел.)
(тыс. руб./чел.)
В отчётном периоде средняя выработка увеличилась на
15,71 тыс. руб./чел. или на 22,45% по сравнению с уровнем базисного периода.
Индекс структурных сдвигов, характеризующий
динамику средней себестоимости в относительном выражении под воздействием
изменения структуры численности, рассчитывается по формуле:
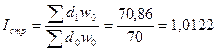
Разность между числителем и знаменателем индекса
отражает абсолютное изменение средней производительности за счёт изменения
структуры численности:
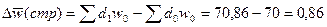 (тыс. руб./чел.)
(тыс. руб./чел.)
В отчётном периоде средняя выработка увеличилась на
0,86 тыс. руб./чел. или на 1,22% по сравнению с уровнем базисного периода в
результате изменения структуры численности.
Индекс фиксированного состава, характеризующий
влияние изменения индивидуальных значений производительности на динамику
среднего показателя:
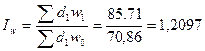
Разность между числителем и знаменателем индекса
показывает абсолютное изменение средней производительности за счёт изменений производительности
по каждой организации:
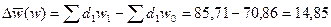 (тыс. руб./чел.)
(тыс. руб./чел.)
В отчётном периоде выработка на каждом предприятии
увеличилась в среднем на 20,97%, что привело к росту средней производительности
на 14,85 тыс. руб./чел.
Проверим взаимосвязь индексов, а также взаимосвязь
абсолютных приростов:
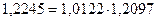
15,71 = 0,86 + 14,85
Средняя производительность возросла в отчётном периоде на 15,71
тыс. руб./чел. или на 22,45%. К этому привёл рост производительности на каждом
предприятии в среднем на 20,97% в результате чего средняя производительность
увеличилась на 14,85 тыс. руб./чел. Изменение структуры численности привело к
росту средней производительности на 0,86 тыс. руб./чел. или на 1,22%.
3. Аналитическая часть
В
данной части работы по данным по 266 компаниям США (приложение 1) проанализируем
вариацию объёма продаж. Для этого выполним следующее:
С
помощью функции «Выборка» встроенного пакета «Анализ данных» MS Excel сформируем выборку из 80 компаний.
Построим
ряд распределения компаний по изучаемому признаку.
По
результатам распределения рассчитаем среднее значение, моду, медиану,
показатели асимметрии и эксцесса.
Элементы диалогового окна «Выборка»
Входной диапазон
Вводим
ссылку на блок данных на рабочем листе, содержащем значения генеральной
совокупности (номера компаний).
Метод выборки – случайный.
Число выборок
Вводим
в поле число случайных значений, которые необходимо разместить в выходном
столбце (80). Позиция каждой извлекаемой переменной во входном диапазоне
выбирается случайно, и любое исходное значение может быть выбрано более одного
раза. По этой причине удаляем повторяющиеся номера и повторяем процедуру
выборки до тех пор, пока не получим 80 различных номеров.
Выходной диапазон
Вводим
ссылку на левую верхнюю ячейку выходного диапазона. Выходные данные будут
записаны в виде одного столбца.
В
результате выборки получена следующая совокупность (таблица 3.1).
Таблица 3.1
|
№
|
Объём продаж,
млн. дол.
|
|
108
|
7,7640
|
|
230
|
8,5160
|
|
265
|
8,7410
|
|
262
|
16,6890
|
|
227
|
20,5750
|
|
236
|
21,4070
|
|
226
|
26,7510
|
|
96
|
33,2650
|
|
235
|
51,3130
|
|
116
|
52,4550
|
|
98
|
52,8760
|
|
209
|
54,5490
|
|
36
|
62,4180
|
|
208
|
69,9520
|
|
40
|
97,9660
|
|
192
|
100,7820
|
|
73
|
141,2580
|
|
113
|
153,2290
|
|
102
|
156,4580
|
|
193
|
165,7970
|
|
253
|
196,3030
|
|
111
|
198,9010
|
|
110
|
201,4650
|
|
216
|
211,3230
|
|
80
|
220,3790
|
|
172
|
227,4490
|
|
93
|
255,1320
|
|
167
|
263,9048
|
|
194
|
274,8440
|
|
179
|
297,5686
|
|
184
|
306,9397
|
|
27
|
308,7327
|
|
239
|
316,8147
|
|
7
|
323,8606
|
|
251
|
344,7937
|
|
258
|
363,9839
|
|
114
|
367,9246
|
|
257
|
390,8726
|
|
171
|
419,6470
|
|
32
|
425,0828
|
|
23
|
445,6387
|
|
191
|
488,2327
|
|
158
|
567,3650
|
|
197
|
578,7107
|
|
237
|
585,6597
|
|
180
|
677,8489
|
|
2
|
690,6001
|
|
173
|
779,3450
|
|
211
|
847,9527
|
|
17
|
884,6189
|
|
30
|
910,8406
|
|
10
|
985,8537
|
|
81
|
1 082,4927
|
|
83
|
1 112,0386
|
|
196
|
1 154,8477
|
|
221
|
1 260,2349
|
|
164
|
1 306,0867
|
|
60
|
1 314,6299
|
|
112
|
1 497,0076
|
|
46
|
1 667,6016
|
|
94
|
1 710,4700
|
|
75
|
1 852,0896
|
|
90
|
2 014,7056
|
|
141
|
2 072,4412
|
|
4
|
2 357,8206
|
|
78
|
2 362,1326
|
|
201
|
2 466,0000
|
|
45
|
2 609,0000
|
|
86
|
2 878,4956
|
|
1
|
3 221,8088
|
|
188
|
3 479,4573
|
|
199
|
3 711,2029
|
|
219
|
3 981,0000
|
|
50
|
4 309,5820
|
|
87
|
4 312,0507
|
|
129
|
4 660,8945
|
|
123
|
4 701,1210
|
|
147
|
6 997,7754
|
|
61
|
7 869,6914
|
|
155
|
28 607,5030
|
Данные
ранжированы в порядке возрастания объёма продаж.
С
помощью функции «Гистограмма» меню СЕРВИС – АНАЛИЗ ДАННЫХ построим ряд
распределения компаний по результатам выборки.
Элементы диалогового окна «Гистограмма»
Входной диапазон
Ссылка
на диапазон, содержащий анализируемые данные.
Новый лист
Устанавливаем
переключатель, чтобы открыть новый лист в книге и вставить результаты анализа.
Вывод графика
Устанавливаем
флажок для автоматического создания встроенной диаграммы на листе, содержащем
выходной диапазон
В
результате получено следующее распределение (таблица 3.2, рисунок 3.1).
Таблица 3.2
|
Карман
|
Частота
|
|
7,764
|
1
|
|
3582,731
|
70
|
|
7157,699
|
7
|
|
10732,67
|
1
|
|
14307,63
|
0
|
|
17882,6
|
0
|
|
21457,57
|
0
|
|
25032,54
|
0
|
|
Еще
|
1
|
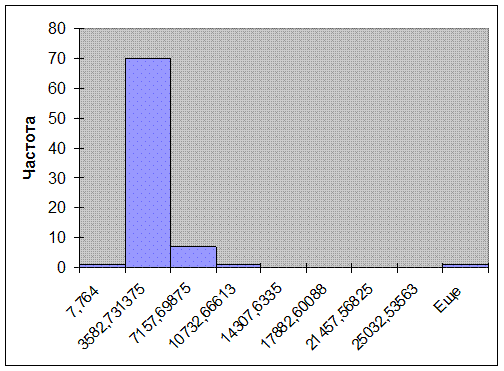
Рисунок 3.1. Гистограмма распределения
компаний по объёму продаж
Ряд
распределения, полученный таким образом, не удовлетворяет следующим
требованиям:
-
отсутствие пустых и малонаполненных групп,
-
отсутствие групп, в которые попадает более половины всей совокупности.
Для
устранения этого недостатка построим ряд с неравными интервалами. Чаще всего
число групп в вариационном ряду устанавливают, придерживаясь формулы,
рекомендованной американским статистиком Стерджессом:
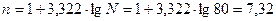
Примем
число групп равным 8.
Неравные
интервалы могут быть прогрессивно возрастающими, прогрессивно убывающими или
равнонаполненными. Построим ряд с прогрессивно возрастающими интервалами.
Если
вариационный ряд построен с неравными интервалами, то для сопоставимости нужно
частоты привести к единице интервала. Полученное отношение называется
плотностью распределения которая рассчитывается по формуле:
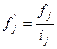
где
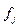 – абсолютная плотность
распределения в j – м интервале;
– абсолютная плотность
распределения в j – м интервале;
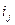 - ширина j – го интервала.
- ширина j – го интервала.
Плотность
распределения используется как для расчёта обобщающих показателей, так и для
графического изображения вариационных рядов с неравными интервалами.
В
таблице 3.3. представлен полученный ряд распределения.
Таблица 3.3
Распределение
компаний по объёму продаж
|
Группы компаний
по объёму продаж, млн. дол.
|
Число
компаний
|
Интервал
|
Плотность
распределения
|
|
7
|
55
|
11
|
48
|
0,22917
|
|
55
|
200
|
11
|
145
|
0,07586
|
|
200
|
310
|
10
|
110
|
0,09091
|
|
310
|
500
|
10
|
190
|
0,05263
|
|
500
|
1000
|
10
|
500
|
0,02000
|
|
1000
|
2000
|
10
|
1000
|
0,01000
|
|
2000
|
3500
|
9
|
1500
|
0,00600
|
|
3500
|
7000
|
9
|
3500
|
0,00257
|
|
|
|
80
|
Х
|
0,48714
|
Из
таблицы видно, что распределение отличается от нормального, поскольку
наибольшая плотность распределения в первой и второй группах.
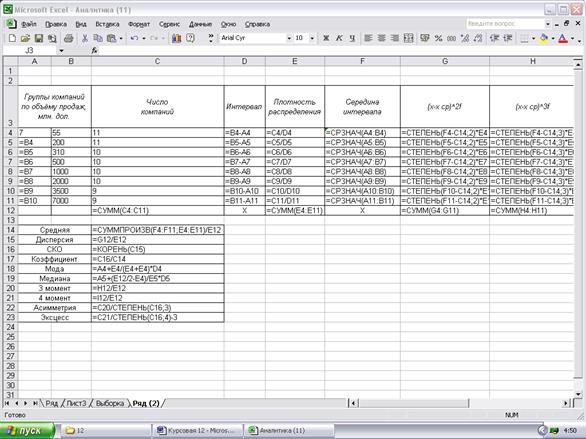
Произведём дополнительные расчёты для уточнения характера
распределения.
Результаты вспомогательных расчётов представлены в таблице 3.4. (для
последнего интервала установлена условная граница). Печать этой таблицы в
режиме формул представлена в приложении 2.
Таблица 3.4
|
Группы компаний
по объёму продаж, млн. дол.
|
Плотность
распределения
|
Середина
интервала
|
(x-x ср)^2f
|
(x-x ср)^3f
|
(x-x ср)^4f
|
|
7
|
55
|
0,22917
|
31
|
10886,0193
|
-2372618,6
|
517114545,2
|
|
55
|
200
|
0,07586
|
127,5
|
1118,99135
|
-135902,6
|
16505503,59
|
|
200
|
310
|
0,09091
|
255
|
3,32642191
|
20,1215921
|
121,71591
|
|
310
|
500
|
0,05263
|
405
|
1281,64719
|
199999,788
|
31209770,83
|
|
500
|
1000
|
0,02000
|
750
|
5021,00241
|
2515768,33
|
1260523258
|
|
1000
|
2000
|
0,01000
|
1500
|
15651,2365
|
19580464,1
|
24496120399
|
|
2000
|
3500
|
0,00600
|
2750
|
37531,4772
|
93868064,3
|
2,34769E+11
|
|
3500
|
7000
|
0,00257
|
5250
|
64312,6919
|
321630925
|
1,60849E+12
|
|
|
|
0,48714
|
Х
|
135806,392
|
435286720
|
1,86958E+12
|
Средняя
арифметическая определяется по формуле:
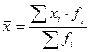
Дисперсия
признака – это средний квадрат отклонений вариантов от их средней величины и
рассчитывается по формуле:
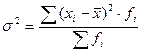
Среднее квадратическое отклонение показывает на сколько в среднем отклоняются
конкретные варианты от их среднего значения и численно равно корню квадратному
из дисперсии:
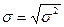
Коэффициент вариации:
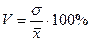
Если
значение коэффициента меньше 40%, то говорят, что вариация признака в
совокупности незначительна, а совокупность однородна в отношении данного
признака.
Мода
– это наиболее часто встречающееся значение признака в совокупности. Значение
моды в ряду распределения определяется как значение признака, имеющего
наибольшую частоту. Значение моды для интервального ряда рассчитывается по
формуле:
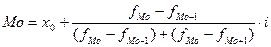
где
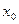 - нижняя граница
модального интервала;
- нижняя граница
модального интервала;
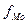 - частота модального
интервала,
- частота модального
интервала,
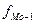 - частота предыдущего
интервала,
- частота предыдущего
интервала,
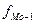 - частота следующего
за модальным интервала,
- частота следующего
за модальным интервала,
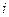 - величина интервала.
- величина интервала.
Модальным
интервалом является интервал с наибольшей частотой. Внутри этого интервала
находят условное значение признака, вблизи которого плотность распределения, т.
е. число единиц совокупности приходящегося на единицу измерения варьирующего
признака достигает максимума.
Медиана
– значение признака, которое делит совокупность на 2 равные части, это
значение, стоящее в середине ранжированного ряда.
Для
интервального ряда значение медианы находят по формуле:
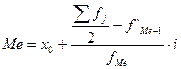
где
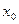 - нижняя граница
медианного интервала;
- нижняя граница
медианного интервала;
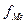 - частота медианного
интервала,
- частота медианного
интервала,
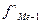 - накопленная частота
предыдущего интервала,
- накопленная частота
предыдущего интервала,
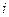 - величина интервала.
- величина интервала.
Асимметрия
рассчитывается по формуле:
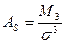
где
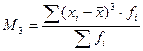 - центральный момент
третьего порядка.
- центральный момент
третьего порядка.
Эксцесс
определяется по формуле:
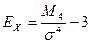
где
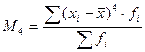 - центральный момент
четвёртого порядка.
- центральный момент
четвёртого порядка.
Расчёты
дали следующие результаты (таблица 3.5):
Таблица 3.5
|
Средняя
|
248,9510
|
|
Дисперсия
|
278782,608
|
|
СКО
|
527,9987
|
|
Коэффициент
вариации
|
2,121
|
|
Мода
|
31
|
|
Медиана
|
82,5308
|
|
3 момент
|
893554163
|
|
4 момент
|
3,8379E+12
|
|
Асимметрия
|
6,0704707
|
|
Эксцесс
|
46,380861
|
Из
таблицы видно следующее:
Средний объём продаж составляет 248,9510 млн. дол.
В данной совокупности наиболее часто
встречались компании с объёмом продаж 31 млн. дол.
Из 80 компаний объём продаж у 40 составлял
менее чем 82,5308 млн. дол. а у 40 компаний
– больше этого значения.
В среднем отклонение объёма продаж по
каждой компании от их среднего значения
составляет 527,9987 млн. дол., т. е.
индивидуальные значения больше или меньше среднего более чем в 2 раза. Выборка
является неоднородной по признаку объём продаж, т.к. коэффициент вариации намного
больше 40%.
Асимметрия характеризует степень
несимметричности распределения относительно его среднего. В данном случае имеем
правостороннюю асимметрию, т. к. 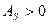 .
.
Эксцесс характеризует относительную
остроконечность или сглаженность распределения по сравнению с нормальным
распределением. Т.к. эксцесс положительный, то это обозначает относительно
остроконечное распределение.
Заключение
Работа показала, что
значение группировки состоит в обобщении данных. Группировка позволяет представить
данные в компактном,
обозримом виде. Кроме того, группировка создает основу для последующей сводки и
анализа данных. Так,
аналитическая группировка позволяет оценить наличие и тесноту связи между
взаимодействующими признаками, структурная группировка помогает
проанализировать структуру статистической совокупности.
Список использованной литературы
1. Общая
теория статистики: Статистическая методология в изучении коммерческой
деятельности: Учебник / Под ред. О. Э. Башиной, А. А. Спирина. – М.: Финансы и
статистика, 1999.
2. Елисеева
И. И., Юзбашев М. М. Общая теория статистики: Учебник – М.: Финансы и статистика,
2001.
3. Статистика:
Курс лекций / Под ред. В. Г. Ионина. – Новисибирск: Изд-во НГАЭиУ, М.: ИНФРА-М,
1999.
4. Глинский
В. В., Ионин В. Г. Статистический анализ. Учебное пособие – М.: Информационно –
издательский центр «Филинъ», 1998.
5. Экономика
и статистика фирм: Учебник / Под ред. С. Д. Ильенковой. – М.: Финансы и
статистика, 1998.
Приложения
Приложение 2
Таблицы аналитической части (режим формул)