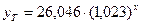Задача 1
По предприятиям легкой промышленности
региона получена информация, характеризующая зависимость объема выпуска
продукции (Y, млн.руб.) от объема капиталовложений
(Х, млн.руб.)
|
y
|
x
|
|
43
|
33
|
|
27
|
17
|
|
32
|
23
|
|
29
|
17
|
|
45
|
36
|
|
35
|
25
|
|
47
|
39
|
|
32
|
20
|
|
22
|
13
|
|
24
|
12
|
Таблица 1.
Требуется:
1.
Найти параметры
уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.
2.
Вычислить
остатки; найти остаточную сумму квадратов; оценить дисперсию остатков 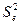 ; построить график остатков.
; построить график остатков.
3.
Проверить
выполнение предпосылок МНК.
4.
Осуществить
проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).
5.
Вычислить
коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05), найти среднюю
относительную ошибку аппроксимации. Сделать вывод о качестве.
6.
Осуществить
прогнозирование среднего значения показателя Y при уровне
значимости α=0,01 при Х=80% от его максимального значения.
7.
Представить
графически фактических и модельных значений Y, точки прогноза.
8.
Составить
уравнения нелинейной регрессии:
·
Гиперболической;
·
Степенной;
·
Показательной.
Привести графики
построенных уравнений регрессии.
9. Для указанных моделей найти коэффициенты детерминации, коэффициенты
эластичности и средние относительные ошибки аппроксимации. Сравнить модели по
этим характеристикам. Сделать вывод.
Решение
1. Параметры
уравнения линейной регрессии.
Уравнение линейной регрессии имеет вид: Y = α0+α1*X
Используя инструментарий Excel, рассчитаем параметры
линейной модели.
Выберем команду “Сервис”, далее – “Анализ данных”.
В диалоговом окне выберем инструмент “Регрессия”.
В диалоговом окне “Регрессия” в поле “Входной интервал Y”
введем диапазон ячеек, содержащих исходные данные Y(x); в поле “Входной интервал
X” введем диапазон ячеек, содержащих исходные данные факторов X; выделим также
заголовки столбцов и установим флажок “Метки”; в поле “Остатки” поставим флажок.
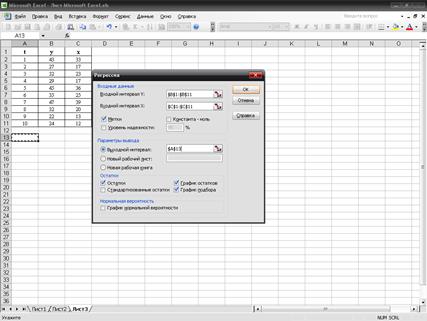
Рис1.
Результаты вычислений представлены в таблицах
2-5:
|
ВЫВОД ИТОГОВ
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
Множественный R
|
0,991332
|
|
|
R-квадрат
|
0,98274
|
|
|
Нормированный
R-квадрат
|
0,980583
|
|
|
Стандартная ошибка
|
1,225755
|
|
|
Наблюдения
|
10
|
|
Таблица 2.
|
Дисперсионный
анализ
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
|
Регрессия
|
1
|
684,3802
|
684,3802
|
455,5021
|
2,44E-08
|
|
|
Остаток
|
8
|
12,01979
|
1,502474
|
|
|
|
|
Итого
|
9
|
696,4
|
|
|
|
|
Таблица 3.
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
|
|
Y-пересечение
|
12,24152
|
1,073194
|
11,40662
|
3,15E-06
|
9,76673
|
14,71631
|
9,76673
|
14,71631
|
|
|
x
|
0,908871
|
0,042585
|
21,34249
|
2,44E-08
|
0,81067
|
1,007073
|
0,81067
|
1,007073
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.
|
ВЫВОД ОСТАТКА
|
|
|
|
|
|
Наблюдение
|
Предсказанное y
|
Остатки
|
|
1
|
42,23428
|
0,765721
|
|
2
|
27,69234
|
-0,69234
|
|
3
|
33,14556
|
-1,14556
|
|
4
|
27,69234
|
1,307664
|
|
5
|
44,96089
|
0,039107
|
|
6
|
34,96331
|
0,036693
|
|
7
|
47,68751
|
-0,68751
|
|
8
|
30,41895
|
1,58105
|
|
9
|
24,05685
|
-2,05685
|
|
10
|
23,14798
|
0,852022
|
Таблица 5.
Коэффициенты модели содержатся в таблице 4 (столбец
Коэффициенты). Таким образом, модель построена, и ее уравнение имеет вид:
Y = 12.24 + 0.91*X
Коэффициент регрессии α1 показывает, что с ростом
объема капвложений (Х) на 1 млн.руб. выпуск
продукции (У) вырастет на 910 тыс.руб.
2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию
остатков 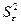 ; построить график остатков.
; построить график остатков.
Остатки модели Ei = yi-yTi содержатся в столбце Остатки программы РЕГРЕССИЯ (таблица 5).
Программой РЕГРЕССИЯ найдены также остаточная
сумма квадратов SSост = 12,02 и дисперсия остатков MSост = 1,51 (таблица 3).
Для построения графика остатков нужно
выполнить следующие действия:
·
Вызвать Мастер диаграмм, выбрать тип диаграммы Точечная (с соединенными точками).
·
Для
указания данных для построения диаграммы зайдем во вкладку Ряд, нажмем кнопку Добавить;
в качестве значений Х укажем исходные
данные Х таблица 1); значения Y – остатки (таблица 5).
Рис2.
В результате получим график остатков:
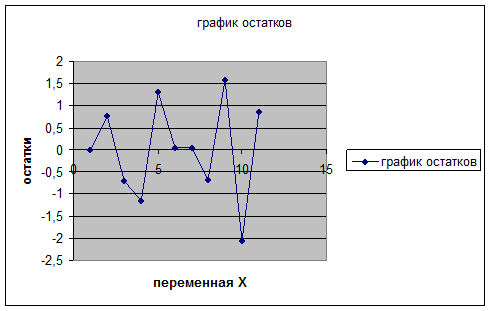
Рис 3.
3. Проверить выполнение
предпосылок МНК.
1) Проведем проверку
случайности остаточной компоненты по критерию поворотных точек.
Количество
поворотных точек определим по графику остатков: р=9.(рис. 3).
Вычислим критическое значение по
формуле, при n = 10.
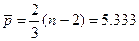
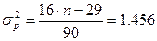
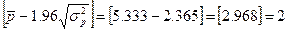
Неравенство
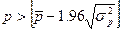 выполняется (9 >2), следовательно, свойство
случайности ряда остатков выполняется.
выполняется (9 >2), следовательно, свойство
случайности ряда остатков выполняется.
2) Свойство
постоянства дисперсии остаточной компоненты проверим по критерию
Голдфельда-Квандта.
Упорядочим
всю таблицу исходных данных по возрастанию факторной переменной Х (Данные => Сортировка).
В переменной X исходных данных (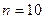 ) выделим первые 5 и последние 5 уровня.
) выделим первые 5 и последние 5 уровня.
С помощью программы РЕГРЕССИЯ построим модель по первым пяти
наблюдениям (регрессия-1), для этой модели остаточная сумма квадратов 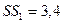 .
.
|
Дисперсионный
анализ
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
|
Регрессия
|
1
|
193,3461
|
193,3461
|
113,6011
|
0,008688
|
|
|
Остаток
|
2
|
3,403946
|
1,701973
|
|
|
|
|
Итого
|
3
|
196,75
|
|
|
|
|
С помощью программы РЕГРЕССИЯ построим модель по последним пяти
наблюдениям (регрессия-2),
для этой модели остаточная сумма квадратов
SS1 = 0,88.
|
Дисперсионный
анализ
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
|
Регрессия
|
1
|
82,11724
|
82,11724
|
186,0469
|
0,005332
|
|
|
Остаток
|
2
|
0,882759
|
0,441379
|
|
|
|
|
Итого
|
3
|
83
|
|
|
|
|
Рассчитаем
статистику критерия: 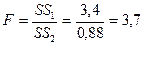
Критическое
значение при уровне значимости 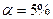 и числах степеней свободы k1=k2=5-1-1=3 составляет
и числах степеней свободы k1=k2=5-1-1=3 составляет  . (Функция FРАСПОБР).(рис. 5).
. (Функция FРАСПОБР).(рис. 5).
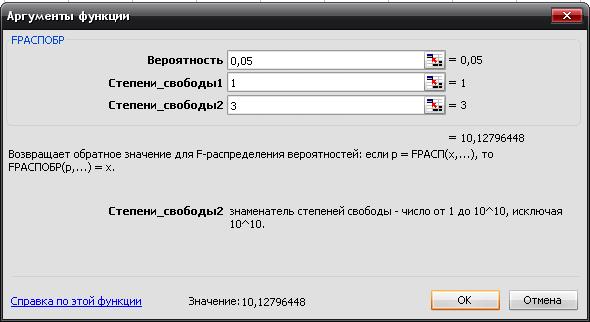
Рис 4.
Схема критерия:

Сравним F=3,7<Fкр=10,13, следовательно,
свойство постоянства дисперсии остатков выполняется, модель гомоскедастичная.
3) Соответствие ряда остатков
нормальному закону распределения проверим с помощью R/S - критерия
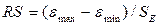
С помощью функции МАКС и
МИН для ряда остатков определим 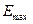 =1,581;
=1,581; 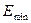 =-2,057. Стандартная ошибка модели найдена программой РЕГРЕССИЯ
и составляет SE = 1,226 (таблица 2).
=-2,057. Стандартная ошибка модели найдена программой РЕГРЕССИЯ
и составляет SE = 1,226 (таблица 2).
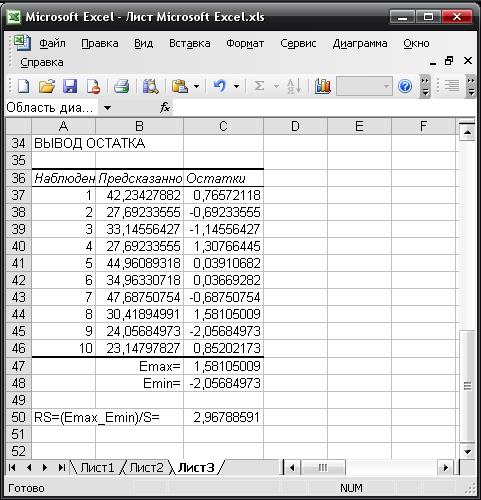
Рис 5.
Тогда R/S = 2,968
Критический интервал
определяется по таблице критических границ отношения R/S и при n = 10 составляет (2,67; 3,57)
2,968 входит
в
(2,67; 3,57), значит, для построенной модели свойство нормального
распределения остаточной компоненты выполняется.
Проведенная проверка
предпосылок регрессионного анализа показала, что для модели выполняются все
условия Гаусса-Маркова, т. е. данная модель является
классической нормальной регрессионной моделью.
4. Осуществить проверку значимости
параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).
t - статистики для коэффициентов уравнения регрессии приведены в
таблице 4. Для свободного коэффициента a0 =12,24 определена статистика t(a0) = 11,41. Для коэффициента регрессии a1 = 0,91, определена статистика t(a1) = 21,34.
Критическое значение tкр = 2,306 найдено для уровня значимости α = 5% и числа
степеней свободы k = 10-1-1 = 8 (рис. 6. Функция СТЬЮДРАСПОБР).
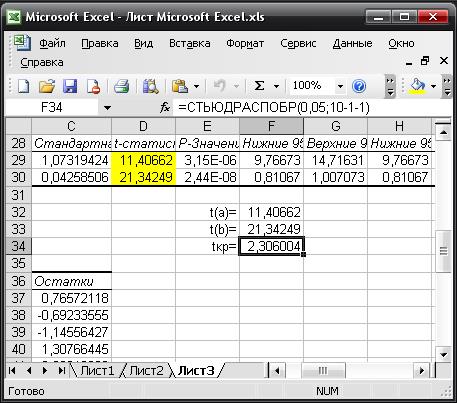
Рис 6.
Схема
критерия:

Сравнение
показывает:
|t(a0) = 11,41| > tкр = 2,306, следовательно, свободный
коэффициент а является значимым.
|t(а1) = 21,34| > tкр = 2,306, следовательно, коэффициент регрессии b является значимым, его и объем капиталовложений нужно
сохранить в модели.
5. Вычислить коэффициент детерминации,
проверить значимость уравнения регрессии с помощью F- критерия Фишера
(α=0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод
о качестве модели.
Коэффициент детерминации R-квадрат определен
программой РЕГРЕССИЯ (таблица 2). И составляет R2 = 0,983 = 98,3%.
Таким образом, вариация (изменение) объема выпуска
продукции (Y) на 98,3% объясняется по полученному уравнению вариацией объема капиталовложений (X).
Проверим значимость полученного
уравнения с помощью F -
критерия Фишера.
F - статистика определена
программой РЕГРЕССИЯ (таблица 3) и составляет F = 455,50.
Критическое значение Fкр = 5,318 найдено для уровня
значимости α = 5% и чисел степеней свободы k1 = 1, k = 8 (рис.
7. Функция FРАСПОБР).
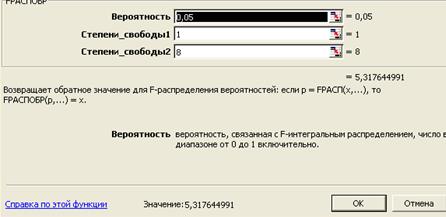
Рис 7.
Сравнение
показывает: F = 455,50 > Fкр = 5,318; следовательно, уравнение модели является значимым,
его использование целесообразно, зависимая переменная Y достаточно хорошо описывается
включенной в модель факторной переменной Х.
Для вычисления средней относительной ошибки аппроксимации рассчитаем
дополнительный столбец относительных погрешностей, которые вычислим по формуле 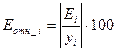 с помощью функции ABS
(Рис 8).
с помощью функции ABS
(Рис 8).
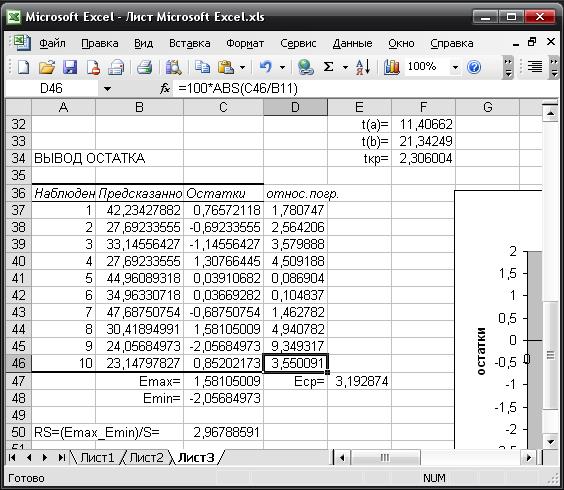
Рис 8.
По столбцу относительных погрешностей найдем среднее значение 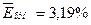 (функция СРЗНАЧ).
(функция СРЗНАЧ).
Схема проверки:

Сравним: 3,19% < 5%, следовательно, модель является точной.
Вывод: на основании
проверки предпосылок МНК, критериев Стьюдента и Фишера и величины коэффициента
детерминации модель можно считать полностью адекватной. Дальнейшее
использование такой модели для прогнозирования в реальных условиях
целесообразно.
6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости 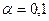 , если прогнозное значение фактора X = 80% от его максимального значения.
, если прогнозное значение фактора X = 80% от его максимального значения.
Рассчитаем по уравнению модели прогнозное значение показателя У
(расчеты представлены на рис 9):
Упр=а0+а2*Хпр=
12,24+0,91*Хпр
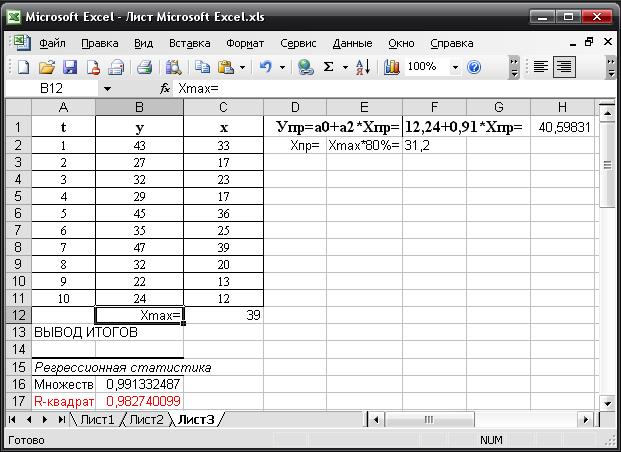
Рис 9.
Таким
образом, если объем капиталовложений составит 31,2 млн. руб., то ожидаемый
объем выпуска продукции составит около 40,60 млн. руб.
Зададим доверительную вероятность 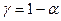 и построим
доверительный прогнозный интервал для среднего значения Y.
и построим
доверительный прогнозный интервал для среднего значения Y.
Для этого нужно рассчитать стандартную ошибку прогнозирования:
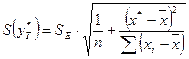
Предварительно подготовим:
- стандартную ошибку
модели 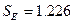 (Таблица 2);
(Таблица 2);
- по столбцу исходных
данных Х найдем среднее значение 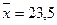 (функция СРЗНАЧ) и
определим
(функция СРЗНАЧ) и
определим 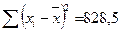 (функция КВАДРОТКЛ).
(функция КВАДРОТКЛ).
Следовательно,
стандартная ошибка прогнозирования для
среднего значения составляет:
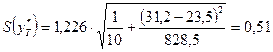
При 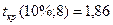 размах доверительного
интервала для среднего значения
размах доверительного
интервала для среднего значения
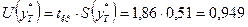
Границами прогнозного интервала будут
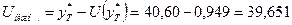
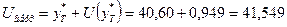
Таким образом, с надежностью 90% можно утверждать, что если объем
капиталовложений составит 31,2 млн. руб., то ожидаемый объем выпуска продукции
будет от 39,65 млн. руб. до 41,55 млн. руб.
7.
Представить графически фактические и модельные значения Y точки прогноза.
Для построения графика используем Мастер диаграмм (точечная) – покажем исходные
данные (поле корреляции).
Покажем
на графике результаты
прогнозирования. Для этого
в опции Исходные
данные добавим ряды:
Имя → прогноз; значения 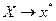 ; значения
; значения 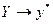 ;
;
Имя → нижняя граница; значения 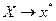 ; значения
; значения 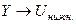 ;
;
Имя → верхняя граница;
значения 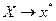 ; значения
; значения 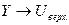
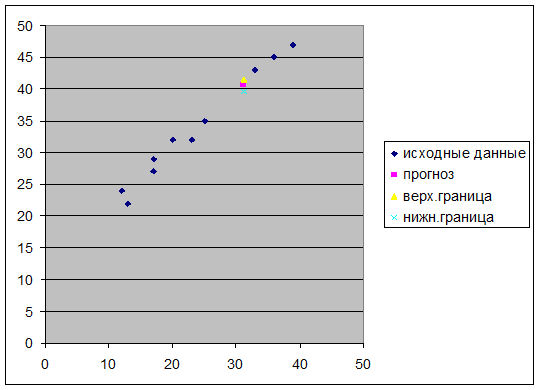
Рис 10.
8. Составить уравнения нелинейной регрессии:
гиперболической; степенной; показательной.
Гиперболическая модель 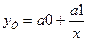 не является
стандартной.
не является
стандартной.
Для ее построения выполним линеаризацию: обозначим 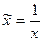 и получим вспомогательную
модель
и получим вспомогательную
модель 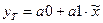 . Вспомогательная модель является линейной. Ее можно построить
с помощью программы РЕГРЕССИЯ, предварительно подготовив исходные данные:
столбец значений
. Вспомогательная модель является линейной. Ее можно построить
с помощью программы РЕГРЕССИЯ, предварительно подготовив исходные данные:
столбец значений 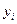 (остается без изменений) и столбец преобразованных значений
(остается без изменений) и столбец преобразованных значений 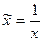 (таблица 6).
(таблица 6).
Таблица 6
|
y
|
x
|
1/х
|
|
24
|
12
|
0,083333
|
|
22
|
13
|
0,076923
|
|
27
|
17
|
0,058824
|
|
29
|
17
|
0,058824
|
|
32
|
20
|
0,05
|
|
32
|
23
|
0,043478
|
|
35
|
25
|
0,04
|
|
43
|
33
|
0,030303
|
|
45
|
36
|
0,027778
|
|
47
|
39
|
0,025641
|
С помощью
программы РЕГРЕССИЯ получим:
|
|
Коэффициенты
|
Стандартная ошибка
|
|
Y-пересечение
|
54,18387
|
2,666196
|
|
1/х
|
-415,749
|
50,279
|
|
|
|
Таким образом, 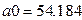 ; а1=-415,749, следовательно, уравнение гиперболической модели
; а1=-415,749, следовательно, уравнение гиперболической модели 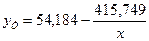 .
.
С помощью полученного
уравнения рассчитаем теоретические
значения 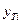 для каждого уровня
исходных данных
для каждого уровня
исходных данных 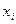 .
.
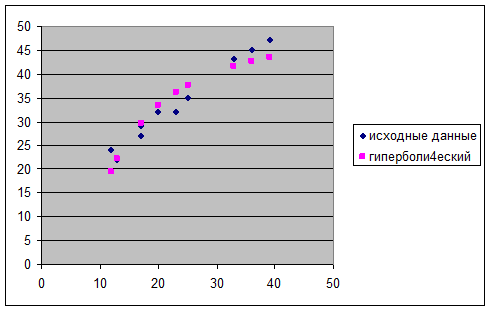
Покажем линию гиперболической модели на
графике. Для этого добавим
к ряду исходных данных 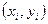 , ряд теоретических
значений
, ряд теоретических
значений 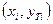 .
.
Степенная модель 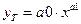 является стандартной. Для
ее построения используем Мастер диаграмм:
исходные данные покажем с помощью точечной диаграммы, затем добавим линию
степенного тренда и выведем на диаграмму уравнение модели.
является стандартной. Для
ее построения используем Мастер диаграмм:
исходные данные покажем с помощью точечной диаграммы, затем добавим линию
степенного тренда и выведем на диаграмму уравнение модели.
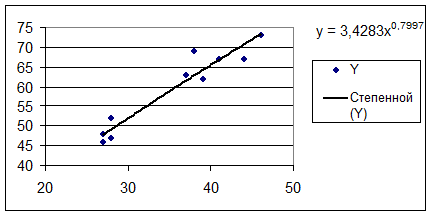
Таким
образом, уравнение степенной модели. 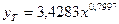
Показательная модель 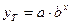 тоже стандартная
(экспоненциальная).
тоже стандартная
(экспоненциальная).
Построим ее с помощью Мастера
диаграмм.
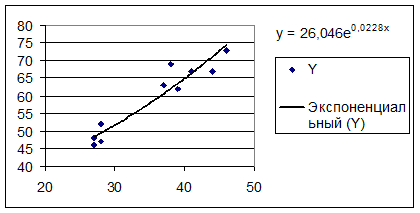
Можно вычислить 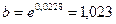 (функция EXP),
тогда уравнение показательной модели
(функция EXP),
тогда уравнение показательной модели