Примечание к работе: во всех задачах данные полученные из задания (исходные данные) выделены курсивом

Примечание к работе: во всех задачах данные полученные из задания (исходные данные) выделены курсивом.

Задача 1

Число детей в семье, f	Число семей сотрудников по подразделениям	x₁*f	x₂*f	x₃*f	x₁²*f	x₂²*f	x₃²*f
первое, x₁	второе, x₂	третье, x₃
0	4	7	5	0	0	0	0	0	0
1	6	10	13	6	10	13	36	100	169
2	3	3	3	6	6	6	18	18	18
3	2	3	4	6	9	12	12	27	48
6				18	25	31	66	145	235

Внутригрупповые средние:

x₁_cp=∑x₁*f/∑f=18/6=3

x₂_cp=∑x₂*f/∑f=25/6=4,167

x₃_cp=∑x₃*f/∑f=31/6=5,167

Общая средняя:

x_cp=(∑x₁*f+∑x₂*f+∑x₃*f)/3*∑f=(18+25+31)/18=4,111

а)Внутригрупповые дисперсии:

σ₁²= x₁²_cp- (x₁_cp)²=∑x₁²*f/∑f-(x₁_cp)²=66/6-3²=2

σ₂²= x₂²_cp- (x₂_cp)²=∑x₂²*f/∑f-(x₂_cp)²=145/6-4,167²=6,803

σ₃²= x₃²_cp- (x₃_cp)²=∑x₃²*f/∑f-(x₃_cp)²=235/6-5,167²=12,469

б)Средняя из внутригрупповых дисперсий:

σ_ср²= (σ₁² *m+σ₂²*n+ σ₃²*к)/(m+n+к)= (2*4+6,803*4+12,469*4)/12=7,191

в)Межгрупповая дисперсия:

δ²=(( x₁_cp- x_cp)²*m+( x₂_cp- x_cp)²*n+( x₂_cp- x_cp)²*к)/(m+n+к)=

( (3-4,111)²*4+(4,167-4,111)²*4 +(5,167-4,111)²*4)/16=0,686

Общая дисперсия:

σ²= x²_cp- x_cp²=(∑x₁²*f+∑x₂²*f+∑x₃²*f)/3*∑f- x_cp²=

(66+145+235)/18-4,111²=7,877

Проверка с помощью правила сложения дисперсий:

σ²= σ_ср²+ δ²

7,877=7,191+0,686

Задача 2

∆<=10%

p=0,5 (вероятность того, что телефонный разговор будет длиться более 5 мин.    такая же как и то, что он будет длиться менее5 мин.)

P=0,954

t=2

Найти необходимый объем выборки n.

∆= t*(p*q/n)^1/2

0,1=2*(0,5*0,5/n)^1/2

n^1/2=10

n=100

Ответ: Необходимый объем выборки 100 телефонных разговоров.

Задача 3

Исходные данные:

Месяцы

Товар, млн.руб.

1

21,2

2

21,3

3

21,2

4

21,3

5

21,2

6

21,0

7

21,0

8

20,2

9

19,2

10

20,1

11

20,8

12

21,1

249,6

а) Сглаживание ряда методом четырехчленной скользящей средней:

Интервал (месяцы)

Товар, млн.руб.

1-4

21,250

2-5

21,250

3-6

21,175

4-7

21,125

5-8

20,850

6-9

20,350

7-10

20,125

8-11

20,075

9-12

20,300

б) Выравнивание ряда динамики по прямой:

Месяцы

Товар, млн.руб., y

Обозначение времени, t

y*t

t²

Выровненные уровни, y_t

1

21,2

-6

-127,2

36

21,321

2

21,3

-5

-106,5

25

21,234

3

21,2

-4

-84,8

16

21,147

4

21,3

-3

-63,9

9

21,060

5

21,2

-2

-42,4

4

20,974

6

21,0

-1

-21

1

20,887

7

21,0

1

21

1

20,713

8

20,2

2

40,4

4

20,626

9

19,2

3

57,6

9

20,540

10

20,1

4

80,4

16

20,453

11

20,8

5

104

25

20,366

12

21,1

6

126,6

36

20,279

249,6

0

-15,8

182

249,6

Уравнение прямой: y_t=a₀+a₁*t

Параметры a₀ и a₁ искомой прямой находятся путем решения системы:

   a₀+a₁*∑t=∑y

   a₀*∑t+a₁*∑t²=∑yt

Т.к. ∑t=0,

   а₀=∑y/n=249,6/12=20,8

   a₁=∑yt/∑t²=-15,8/182=-0,0868

Уравнение искомой прямой:

   y_t=20,8-0,0868*t

Подставляя в это уравнение значения t из таблицы, найдем выровненные (расчетные) уровни.

Из формулы прямой видно, что характер общей тенденции изучаемого явления убывающий, в среднем ежемесячно уменьшается на 868тыс. руб.

Задача 4

Домостроительный комбинат

Построено жилья, тыс. м3, q

Себестоимость 1м³, млн. руб. z

q₀*z₀

q₁*z₁

q₁*z₀

1996

1997

1996

1997

ДСК-1

53

68

1,5

1,7

79,5

115,6

102

ДСК-2

179

127

1,7

1,9

304,3

241,3

215,9

232

195

383,8

356,9

317,9

Индекс себестоимости переменного состава:

I_z¹=(∑q₁*z₁/∑q₁)/ (∑q₀*z₀/∑q₀)=(356,9/195)/(383,8/232)=1,106

Индекс себестоимости постоянного состава:

I_z²=(∑q₁*z₁/∑q₁)/ (∑q₀*z₁/∑q₁)=(356,9/195)/(317,9/195)=1,123

Индекс структурных сдвигов:

I_стр= I_z¹/I_z²=1,106/1,123=0,985

Задача 5

Из исходной таблицы необходимо отобрать 2-3 экономически связанных между собой показателя. Выберем показатели: уставный капитал и среднесписочная численность рабочих:

№

Уставный капит., тыс.руб.

Среднесписочная численность рабочих, чел.

1

5310

725

2

6545

693

3

2219

525

4

10654

539

5

10468

799

6

21374

421

7

7930

505

8

2430

373

9

14630

537

10

21200

401

11

6810

500

12

8410

433

13

12305

334

14

173953

847

15

10479

488

16

9481

517

17

4265

391

18

6670

355

19

9946

368

20

26914

571

21

47421

792

22

9594

367

23

11542

581

24

6771

579

25

12919

538

26

10664

754

27

16410

546

28

17300

734

29

14594

618

30

17861

464

31

34463

504

а) Построим интервальные вариационные ряды по каждому показателю:

Уставный капит., тыс.руб.

Число предприятий, f

0-5000

3

5000-10000

10

10000-20000

12

20000-30000

3

30000-40000

1

40000-50000

1

более 50000

1

Всего:

31

Среднесписочная численность рабочих, чел.

Число предприятий, f

300-400

6

400-500

5

500-600

12

600-700

2

700-800

5

800-900

1

Всего:

31

в)

Уставный капит., тыс.руб.

Число предприятий, f

Середины интервалов уст. капитала, x

f*x

Накопленная частота числа предприятий, s

0-5000

3

2500

7500

3

5000-10000

10

7500

75000

13

10000-20000

12

12500

150000

25

20000-30000

3

15000

45000

28

30000-40000

1

35000

35000

29

40000-50000

1

45000

45000

30

более 50000

1

55000

55000

31

31

412500

Среднесписочная численность рабочих, чел.

Число предприятий, f

Середины интервалов среднеспис. числа рабочих, x

f*x

Накопленная частота числа предприятий, s

300-400

6

350

2100

6

400-500

5

450

2250

11

500-600

12

550

6600

23

600-700

2

650

1300

25

700-800

5

750

3750

30

800-900

1

850

850

31

31

16850

1.     Средний уставный капитал предприятий (как средняя арифметическая взвешенная):

       X_ср=∑x_i*f_i /∑f_i

       X_ср1=412500/31=13306,451 тыс.руб.

     Аналогично, средняя среднесписочная численность рабочих предприятий:

       X_ср2=16850/31=543,548 чел.

2. Модальный размер среднего уставного капитала предприятий:

       М_о=x₀+h*( f₂- f₁)/( ( f₂- f₁)*( f₂- f₃))

    Модальный интервал (10000-20000), т.к. f_max=12

       М_о
1=10000+10000*(12-10)/((12-10)+(12-3))=11818,182 тыс.руб.

Аналогично модальный размер средней среднесписочной численности рабочих предприятий:

     Модальный интервал (500-600), т.к. f_max=12

       М_{о 2}=500+100*(12-5)/((12-5)+(12-2))=541,176 чел.

3. Медиальный размер среднего уставного капитала предприятий:

        М_е= x₀+h*(1/2*∑f_i-Sдо М_е)/f_{мед.инт}

     ∑f_i/2=31+1/2=16 середина интервала. Она попадает

в медиальный интервал (10000-20000).

     М_е=10000 +10000*(1/2*31-13)/12=12083,333 тыс.руб.

Аналогично медиальный размер средней среднесписочной численности рабочих предприятий:

     ∑f_i/2=31+1/2=16 середина интервала. Она попадает

в медиальный интервал (500-600).

    М_е=500 +200*(1/2*31-11)/12=575 тыс.руб.

Задача 6

Крепость нити, г

Середина интервала, г, x

Число проб,

Число проб в % к итогу, f

x*f

x²*f

x-x_cp

t=(x-x_cp)/σ

y_t

f_t

120-130

125

2

0,79%

0,992

124,008

69,683

2,2304

0,03

1,06%

130-140

135

6

2,38%

3,214

433,929

59,683

1,9103

0,06

2,05%

140-150

145

8

3,17%

4,603

667,460

49,683

1,5902

0,11

3,62%

150-160

155

15

5,95%

9,226

1430,060

39,683

1,2701

0,18

5,70%

160-170

165

25

9,92%

16,369

2700,893

29,683

0,9501

0,25

8,13%

170-180

175

29

11,51%

20,139

3524,306

19,683

0,6300

0,33

10,47%

180-190

185

35

13,89%

25,694

4753,472

9,683

0,3099

0,38

12,16%

190-200

195

30

11,90%

23,214

4526,786

0,317

0,0102

0,4

12,77%

200-210

205

25

9,92%

20,337

4169,147

10,317

0,3302

0,38

12,10%

210-220

215

28

11,11%

23,889

5136,111

20,317

0,6503

0,32

10,34%

220-230

225

16

6,35%

14,286

3214,286

30,317

0,9704

0,25

7,97%

230-240

235

10

3,97%

9,325

2191,468

40,317

1,2905

0,17

5,54%

240-250

245

8

3,17%

7,778

1905,556

50,317

1,6105

0,11

3,49%

250-260

255

7

2,78%

7,083

1806,250

60,317

1,9306

0,06

1,98%

260-270

265

5

1,98%

5,258

1393,353

70,317

2,2507

0,03

1,02%

270-280

275

3

1,19%

3,274

900,298

80,317

2,5708

0,02

0,48%

Итого:

-

252

100,00%

194,683

38877,381

-

-

-

98,87%

Найдем x_cp:

   x_cp=∑x*f/ ∑f=194,683

   x²_cp=∑x²*f/ ∑f=38877,381

Среднее квадратическое отклонение:

   σ²= x²_cp- (x_cp)²=38877,381-194,683²=976,09

   σ=√976,09=31,242

Нормальное распределение выражается уравнением:

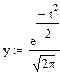
Затем рассчитываем теоретические частоты нормального распределения по формуле:

f_t= y_t*h*∑f/σ,

где h-ширина интервала ряда (h=10), ∑f=1, σ=31,242

Месяцы	Товар, млн.руб.
1	21,2
2	21,3
3	21,2
4	21,3
5	21,2
6	21,0
7	21,0
8	20,2
9	19,2
10	20,1
11	20,8
12	21,1
	249,6

Интервал (месяцы)	Товар, млн.руб.
1-4	21,250
2-5	21,250
3-6	21,175
4-7	21,125
5-8	20,850
6-9	20,350
7-10	20,125
8-11	20,075
9-12	20,300

Месяцы	Товар, млн.руб., y	Обозначение времени, t	y*t	t²	Выровненные уровни, y_t
1	21,2	-6	-127,2	36	21,321
2	21,3	-5	-106,5	25	21,234
3	21,2	-4	-84,8	16	21,147
4	21,3	-3	-63,9	9	21,060
5	21,2	-2	-42,4	4	20,974
6	21,0	-1	-21	1	20,887
7	21,0	1	21	1	20,713
8	20,2	2	40,4	4	20,626
9	19,2	3	57,6	9	20,540
10	20,1	4	80,4	16	20,453
11	20,8	5	104	25	20,366
12	21,1	6	126,6	36	20,279
	249,6	0	-15,8	182	249,6

Домостроительный комбинат	Построено жилья, тыс. м3, q	Себестоимость 1м³, млн. руб. z	q₀*z₀	q₁*z₁	q₁*z₀
1996	1997	1996	1997
ДСК-1	53	68	1,5	1,7	79,5	115,6	102
ДСК-2	179	127	1,7	1,9	304,3	241,3	215,9
	232	195			383,8	356,9	317,9

№	Уставный капит., тыс.руб.	Среднесписочная численность рабочих, чел.
1	5310	725
2	6545	693
3	2219	525
4	10654	539
5	10468	799
6	21374	421
7	7930	505
8	2430	373
9	14630	537
10	21200	401
11	6810	500
12	8410	433
13	12305	334
14	173953	847
15	10479	488
16	9481	517
17	4265	391
18	6670	355
19	9946	368
20	26914	571
21	47421	792
22	9594	367
23	11542	581
24	6771	579
25	12919	538
26	10664	754
27	16410	546
28	17300	734
29	14594	618
30	17861	464
31	34463	504

Уставный капит., тыс.руб.	Число предприятий, f
0-5000	3
5000-10000	10
10000-20000	12
20000-30000	3
30000-40000	1
40000-50000	1
более 50000	1
Всего:	31

Среднесписочная численность рабочих, чел.	Число предприятий, f
300-400	6
400-500	5
500-600	12
600-700	2
700-800	5
800-900	1
Всего:	31

Уставный капит., тыс.руб.	Число предприятий, f	Середины интервалов уст. капитала, x	f*x	Накопленная частота числа предприятий, s
0-5000	3	2500	7500	3
5000-10000	10	7500	75000	13
10000-20000	12	12500	150000	25
20000-30000	3	15000	45000	28
30000-40000	1	35000	35000	29
40000-50000	1	45000	45000	30
более 50000	1	55000	55000	31
	31		412500

Среднесписочная численность рабочих, чел.	Число предприятий, f	Середины интервалов среднеспис. числа рабочих, x	f*x	Накопленная частота числа предприятий, s
300-400	6	350	2100	6
400-500	5	450	2250	11
500-600	12	550	6600	23
600-700	2	650	1300	25
700-800	5	750	3750	30
800-900	1	850	850	31
	31		16850

Крепость нити, г	Середина интервала, г, x	Число проб,	Число проб в % к итогу, f	x*f	x²*f	x-x_cp	t=(x-x_cp)/σ	y_t	f_t
120-130	125	2	0,79%	0,992	124,008	69,683	2,2304	0,03	1,06%
130-140	135	6	2,38%	3,214	433,929	59,683	1,9103	0,06	2,05%
140-150	145	8	3,17%	4,603	667,460	49,683	1,5902	0,11	3,62%
150-160	155	15	5,95%	9,226	1430,060	39,683	1,2701	0,18	5,70%
160-170	165	25	9,92%	16,369	2700,893	29,683	0,9501	0,25	8,13%
170-180	175	29	11,51%	20,139	3524,306	19,683	0,6300	0,33	10,47%
180-190	185	35	13,89%	25,694	4753,472	9,683	0,3099	0,38	12,16%
190-200	195	30	11,90%	23,214	4526,786	0,317	0,0102	0,4	12,77%
200-210	205	25	9,92%	20,337	4169,147	10,317	0,3302	0,38	12,10%
210-220	215	28	11,11%	23,889	5136,111	20,317	0,6503	0,32	10,34%
220-230	225	16	6,35%	14,286	3214,286	30,317	0,9704	0,25	7,97%
230-240	235	10	3,97%	9,325	2191,468	40,317	1,2905	0,17	5,54%
240-250	245	8	3,17%	7,778	1905,556	50,317	1,6105	0,11	3,49%
250-260	255	7	2,78%	7,083	1806,250	60,317	1,9306	0,06	1,98%
260-270	265	5	1,98%	5,258	1393,353	70,317	2,2507	0,03	1,02%
270-280	275	3	1,19%	3,274	900,298	80,317	2,5708	0,02	0,48%
Итого:	-	*252*	100,00%	194,683	38877,381	-	-	-	98,87%