Примечание к работе: во всех задачах данные полученные из задания (исходные данные) выделены курсивом.

Задача 1

I  группа пряжи (менее крепкая)	II группа пряжи (более крепкая)
Крепость нити, г	Середина интервала, г, f1	Число проб, x1	x1*f1	x12*f1	Крепость нити, г	Середина интервала, г, f2	Число проб, x2	x2*f2	x22*f2
120-130	125	2	250	500	200-210	205	25	5125	128125
130-140	135	6	810	4860	210-220	215	28	6020	168560
140-150	145	8	1160	9280	220-230	225	16	3600	57600
150-160	155	15	2325	34875	230-240	235	10	2350	23500
160-170	165	25	4125	103125	240-250	245	8	1960	15680
170-180	175	29	5075	147175	250-260	255	7	1785	12495
180-190	185	35	6475	226625	260-270	265	5	1325	6625
190-200	195	30	5850	175500	270-280	275	3	825	2475
	1280		26070	701940		1920		22990	415060

Внутригрупповые средние:                                                                                                                                                                                                                                                                                                                                                                                    

   x_1cp=∑x₁*f₁/∑f₁=26070/1280=20,367

   x_2cp=∑x₂*f₂/∑f₂=22990/1920=11,974

Общая средняя:

   x_cp=(∑x₁*f₁+∑x₂*f₂)/( ∑f₁+∑f₂)=(26070+22990)/(1280+1920)=15,331

Внутригрупповые дисперсии:

   σ₁²= x₁²_cp- (x_1cp)²=∑x₁²*f₁/∑f₁-(x_1cp)²=701940/1280-20,367²=133,576

   σ₂²= x₂²_cp- (x_2cp)²=∑x₂²*f₂/∑f₂-(x_2cp)²=415060/1920-11,974²=72,800

Средняя из внутригрупповых дисперсий:

   σ_ср²= (σ₁² *m+σ₂²*n)/(m+n)= (133,576*8+72,800*8)/16=103,188

Межгрупповая дисперсия:

    δ²=(( x_1cp- x_cp)²*m+( x_2cp- x_cp)²*n)/(m+n)=

   ( (20,367-15,331)²*8+(11,974-15,331)²*8 )/16=18,315

Общая дисперсия:

   σ²= σ_ср²+ δ²=103,188+18,315=121,503

                                                              

Задача 2

N=67800

σ²=140 руб.

P=0,997

∆<=10 руб.

t=3

∆=t*(σ²/n*(1-n/N))^1/2

10>=3*(140/n*(1-n/67800)^1/2

100>=9*(140/n-7/3390)

n>=12,6

Ответ: необходимо выбрать не менее 12,6 лицевых счетов, т.е. 13.

Задача 3

Годы	Выработка прод. на одного раб., тыс.руб., q	Фондоот Дача, тыс.руб., Н	Э/вооруженность, кВт-ч/чел.-ч, Э	Уд. вес материалов в с/с, %, м	q*э	q*м	э*м	q2	э2	м2
1983	42,3	23	0,72	95,00%	30,456	40,185	0,684	1789,29	0,518	90,25%
1984	44,2	21	0,68	96,10%	30,056	42,476	0,653	1953,64	0,462	92,35%
1985	55,5	16	1,22	97,20%	67,710	53,946	1,186	3080,25	1,488	94,48%
1986	43,8	10	1,02	95,20%	44,676	41,698	0,971	1918,44	1,040	90,63%
1987	34,3	8,1	0,93	95,20%	31,899	32,654	0,885	1176,49	0,865	90,63%
1988	42,3	5,5	1,11	94,40%	46,953	39,931	1,048	1789,29	1,232	89,11%
1989	37,9	3,9	0,93	94,80%	35,247	35,929	0,882	1436,41	0,865	89,87%
1990	32,6	5,3	1,01	94,00%	32,926	30,644	0,949	1062,76	1,020	88,36%
1991	42,4	4,9	3,03	92,90%	128,472	39,390	2,815	1797,76	9,181	86,30%
1992	42,9	3,7	5,72	92,60%	245,388	39,725	5,297	1840,41	32,718	85,75%
1993	60,5	5,4	4,8	80,50%	290,400	48,703	3,864	3660,25	23,040	64,80%
1994	61,5	5	2,5	93,60%	153,750	57,564	2,340	3782,25	6,250	87,61%
1995	70,7	5,9	8,6	93,90%	608,020	66,387	8,075	4998,49	73,960	88,17%
1996	80,5	6,8	6	94,90%	483,000	76,395	5,694	6480,25	36,000	90,06%
1997	85,1	6,7	7,8	95,60%	663,780	81,356	7,457	7242,01	60,840	91,39%
	776,5	131	46,07	1405,90%	2892,733	726,982	42,800	44007,99	249,481	1319,77%

Средние показатели:

q_ср=∑q/n=776,5/15=51,767

э_ср=∑э/n=46,07/15=3,071

m_ср=∑m/n=1405,9/15=93,727%

Средние квадратов показателей:

q²_ср=∑q²/n=44007,99/15=2933,866

э²_ср=∑э²/n=249,481/15=16,632

m²_ср=∑m²/n=1319,77/15=87,9847%

Средние попарные произведения показателей:

(q*э)_ср=∑q*э /n=2892,733/15=192,8

(q*m)_ср=∑q*m /n=726,982/15=48,465

(э*m)_ср =∑q*m /n =42,8/15=2,853

Средние квадратические отклонения:

 σ_q=(q²_cp- q_cp²)^1/2=2933,866-51,767²=254,044

 аналогично:

  σ_э=16,632-3,071²=7,201

  σ_m=87,9847-(93,727)²=87,9847%-87,8469%=0,1378%

а) Парные коэффициенты корреляции:

  r_qэ=( (q*э)_ср- q_ср*э_ср)/σ_q*σ_э=

  (192,8-51,767*3,071)/254,044*7,201=0,0185

Между выработкой продукции промышленности на одного рабочего и электровооруженностью существует прямая связь (т.к. r_qэ>0).

r_qm=( (q*m)_ср- q_ср*m_ср)/σ_q*σ_m=

(48,465-51,767*93,727%)/ 254,044*0,1378%=-0,156

Между выработкой продукции промышленности на одного рабочего и удельным весом материалов в себестоимости существует обратная связь.

r_эm=( (э*m)_ср- э_ср*m_ср)/σ_э*σ_m=

(2,853-3,071*93,727%)/ 7,201*0,1378%=-0,0256

Между электровооруженностью и удельным весом материалов в себестоимости существует обратная связь.

Задача 4

Вид мебели	Общие затраты времени, t	Индивид. индексы произв. труда, iw	Индивид. индексы  времени, it	Индивид. индексы физического объема продукции, iq
Май	июнь
Мягкая	19,2	19,0	1,02	0,990	1,009
Корпусная	9,5	9,5	1,01	1	1,01
Кухонная	14,3	13,9	1,04	0,972	1,011

Индивидуальные индексы затрат времени рассчитываются по формуле:

 i_t=t₁ /t₀

Т.к. q=t*w, то индивидуальные индексы физического объема находятся, как произведение индивид. индексов этих же показателей:

i_q=i_t*i_w

Задача 5

Группы предприятий по числу работающих	Число предприятий,	Середины интервалов групп предприятий, x	Число предприятий в % к итогу, f	x*f	x2*f	x-xcp	t=(x-xср)/ σ	yt	ft
100-200	1	150	1,3%	1,875	281,25	360,00	2,9010	0,006	0,47%
200-300	3	250	3,8%	9,375	2343,75	260,00	2,0951	0,044	3,46%
300-400	7	350	8,8%	30,625	10718,8	160,00	1,2893	0,174	13,70%
400-500	30	450	37,5%	168,75	75937,5	60,00	0,4835	0,355	27,95%
500-600	19	550	23,8%	130,625	71843,8	40,00	0,3223	0,379	29,84%
600-700	15	650	18,8%	121,875	79218,8	140,00	1,1282	0,396	31,18%
700-800	5	750	6,3%	46,875	35156,3	240,00	1,9340	0,061	4,80%
	80	3150	100,0%	510	275500				111,42%

Найдем x_cp:

   x_cp=∑x*f/ ∑f=510

   x²_cp=∑x²*f/ ∑f=275500

Среднее квадратическое отклонение:

   σ²= x²_cp- (x_cp)²=275500-510²=15400

   σ=√15400=124,1

Нормальное распределение выражается уравнением:

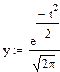
Затем рассчитываем теоретические частоты нормального распределения по формуле:

f_t= y_t*h*∑f/σ,

где h-ширина интервала ряда (h=100), ∑f=1, σ=124,1

Задача 6

Из исходной таблицы необходимо отобрать 2-3 экономически связанных между собой  показателя. Выберем показатели: уставный капитал и среднесписочная численность рабочих:

№	Уставный капит., тыс.руб.	Среднесписочная численность рабочих, чел.
1	5310	725
2	6545	693
3	2219	525
4	10654	539
5	10468	799
6	21374	421
7	7930	505
8	2430	373
9	14630	537
10	21200	401
11	6810	500
12	8410	433
13	12305	334
14	173953	847
15	10479	488
16	9481	517
17	4265	391
18	6670	355
19	9946	368
20	26914	571
21	47421	792
22	9594	367
23	11542	581
24	6771	579
25	12919	538
26	10664	754
27	16410	546
28	17300	734
29	14594	618
30	17861	464
31	34463	504

а) Построим интервальные вариационные ряды по каждому показателю:

Уставный капит., тыс.руб.	Число предприятий, f
0-5000	3
5000-10000	10
10000-20000	12
20000-30000	3
30000-40000	1
40000-50000	1
более 50000	1
Всего:	31

Среднесписочная численность рабочих, чел.	Число предприятий, f
300-400	6
400-500	5
500-600	12
600-700	2
700-800	5
800-900	1
Всего:	31

в)

Уставный капит., тыс.руб.	Число предприятий, f	Середины интервалов уст. капитала, x	f*x	Накопленная частота числа предприятий, s
0-5000	3	2500	7500	3
5000-10000	10	7500	75000	13
10000-20000	12	12500	150000	25
20000-30000	3	15000	45000	28
30000-40000	1	35000	35000	29
40000-50000	1	45000	45000	30
более 50000	1	55000	55000	31
	31		412500

Среднесписочная численность рабочих, чел.	Число предприятий, f	Середины интервалов среднеспис. числа рабочих, x	f*x	Накопленная частота числа предприятий, s
300-400	6	350	2100	6
400-500	5	450	2250	11
500-600	12	550	6600	23
600-700	2	650	1300	25
700-800	5	750	3750	30
800-900	1	850	850	31
	31		16850

1.     Средний уставный капитал предприятий (как средняя арифметическая взвешенная):

       X_ср=∑x_i*f_i /∑f_i

       X_ср1=412500/31=13306,451 тыс.руб.

     Аналогично, средняя среднесписочная численность рабочих предприятий:

       X_ср2=16850/31=543,548 чел.

2. Модальный размер среднего уставного капитала предприятий:

       М_о=x₀+h*( f₂- f₁)/( ( f₂- f₁)*( f₂- f₃))

    Модальный интервал (10000-20000), т.к. f_max=12

       М_{о 1}=10000+10000*(12-10)/((12-10)+(12-3))=11818,182 тыс.руб.

Аналогично модальный размер средней среднесписочной численности рабочих предприятий:

     Модальный интервал (500-600), т.к. f_max=12

       М_{о 2}=500+100*(12-5)/((12-5)+(12-2))=541,176 чел.

3. Медиальный размер среднего уставного капитала предприятий:

        М_е= x₀+h*(1/2*∑f_i-Sдо М_е)/f_{мед.инт}

     ∑f_i/2=31+1/2=16  середина интервала. Она попадает

в медиальный интервал (10000-20000).

     М_е=10000 +10000*(1/2*31-13)/12=12083,333 тыс.руб.

Аналогично медиальный размер средней среднесписочной численности рабочих предприятий:

     ∑f_i/2=31+1/2=16  середина интервала. Она попадает

в медиальный интервал (500-600).

    М_е=500 +200*(1/2*31-11)/12=575 тыс.руб.