1. Дайте логическую характеристику следующих понятий: а) красный день календаря; б) созвездие; в) внеземная цивилизация.

Произведите с этими понятиями операции определения, обобщения, ограничения (определение данных понятий проверьте по правилам топики, дополнения к классу

Понятия не являются врожденными или автоматически приобретаемыми в опыте. Они – продукт специальной умственной деятельности, которую мы будем называть конструированием (определением). Сконструировать понятие в общем случае означает выяснить его содержание и объем.

Понятия разделяются прежде всего на индивидуальные, или единичные, и общие. Индивидуальными понятиями мы будем называть те понятия, которые относятся к предметам единичным, индивидуальным (в данном случае индивидуальные понятия совпадают с пред­ставлениями о единичных вещах), например: «британский посланник во Франции», «высочайшая гора в Америке», «автор «Мертвых душ», «эта книга». К числу единичных понятий от­носятся также и собственные имена, например: «Казбек», «Ньютон», «Рим». Понятия, которые относятся к группе или классу предметов или явлений, имеющих известное сходство между собой, называются общими понятиями или классо­выми понятиями. Например, понятия «растение», «животное», «газ», «двигатель», «поступок», «движение», «красота», «гнев», «чувство» и т. п. суть понятия классовые или общие.

Таким образом все рассматриваемые нами понятия относятся к классовым понятиям, понятиям общего вида.

Понятие «красный день календаря» является конкретным, т.к. определяет событие имеющее определенное существо­вание.

Понятие «созвездие» представляет собой собирательный термин, т.к. мы имеем в виду, что они служит для обозначения целого, составленного из однородных единиц.

Понятие «внеземная цивилизация» является абстрактным, т.к. это понятие такой вещи, которая не может восприниматься нами как известная определенная вещь.

Процесс образования менее общих понятий из более общих называется ограничением (determlnatio). Для образования менее общего понятия мы должны к более об­щему прибавить несколько признаков, благодаря чему по­нятие уясняется (determinatur). Обратный процесс образования более общего понятия из менее общего, при котором, наоборот, некоторое количество признаков от данного понятия отни­мается, называется обобщением (generalisatio).

Род образуется из видов при помощи процесса обобщения, и, наоборот, виды образуются из родов при помощи процесса ограничения. Эти процессы мы можем изобразить при помощи следующей схемы:

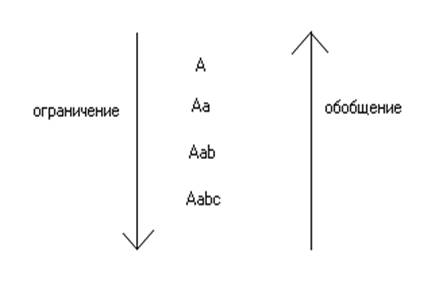
Обратный процесс - получение более общих понятий путем отбрасывания отдельных признаков - будет называться обобщением. И тот и другой процесс можно изобразить при помощи следующей схемы, в которой стрелки показывают или нисхождение от более общих понятий к менее общим или, наобо­рот, восхождение от менее общих к более общим понятиям[1].

Таким, образом:

1) Красный день календаря – пустое, абстрактное, относительное, положительной, несобирательное.

2) Созвездие – общее, частное, безотносительное, положительное, собирательное.

3) Внеземная цивилизация – единичное, абстрактное, относительное, отрицательное, несобирательное.

2. Дайте объединенную классификацию суждений, приведите их схемы и принятые в логике обозначения (А, Е, I, О). Укажите распределение терминов и изобразите их соотношение с помощью круговых схем Эйлера

2.1. «Философ не есть человек коллективного родового сознания»

2.2. Незаконный договор является недействительным

2.3. Денежной единицей в Российской Федерации является рубль

2.4. Большинство студентов юридических вузов изучают конфликтологию

Объединяя количественную и качественную характеристики, суждения делятся на общеутвердительные, общеотрицательные, частноутвердительные, частноотрицательные.

Общеутвердительное суждение - это суждение, общее по количеству и утвердительное по качеству. Общеотрицательное суждение - суждение, общее по количеству и отрицательное по качеству. Частноутвердительное суждение - суждение, частное по количеству и утвердительное по качеству. Частноотрцательное суждение - суждение, частное по количеству и отрицательное по качеству.

Для краткости их обозначе­ния в логике принято употреблять следующие символы. Для обще-утвердительного суждения берут символ А, первую гласную глагола affirmo - утверждаю; для частно-утвердитель­ного - I, вторую гласную того же глагола; для обще-отрица­тельного - Е, первую гласную глагола nego - отрицаю; для частно-отрицательного - О, вторую гласную того же глагола.

Таким образом, символы суждений мы можем обозначить при помощи следующей таблицы:

А  Все S суть Р.

I Некоторые S суть Р.

Е Ни одно S не есть Р.

О Некоторые S не суть Р.

Выясним отно­шение между подлежащим и сказуемым во всех этих классах суждений.

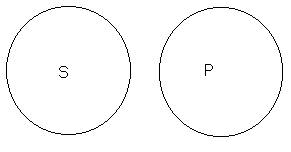
Суждения О. Возьмем частно-отрицательное суждение  «Незаконный договор является недействительным. В суждении отрицается всякое совпадение между подлежащим и сказуемым; один класс находится вне другого класса. Мы в мышлении совершенно от­деляем класс подлежащего от класса сказуемого. Символиче­ски отношение S к Р в таких суждениях может быть обозначено посредством двух отдельно стоящих и не связанных друг с дру­гом кругов.

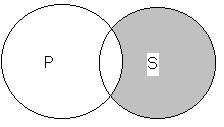
Суждения Е. Возьмем обще-отрицательное суждение - суждение «Философ не есть человек коллективного родового сознания». Это суждение означает, что философ не входит в класс людей коллективного родового сознания, другими сло­вами, некоторая часть S не входит в объем Р. Если мы предста­вим подлежащее и сказуемое в суждении О в виде кругов, то эти круги должны иметь и общие и не общие части, т.е. они должны пересекаться. Заштрихованная часть круга озна­чает, что об этой части субъекта идет речь в этом суждении, а именно, что она не входит в объем понятия Р, что она нахо­дится вне понятия Р. Таким образом, для суждения О мы по­лучаем тот же символ, что и для класса суждений I. Разница между их символами та, что в суждениях I мы обращаем внима­ние на то, что есть совпадающего между S и Р, а в суж­дениях О - на то, что есть не совпадающего между, ними.

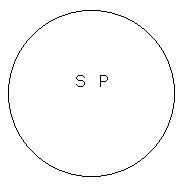
Суждения А. Возьмем обще-утвердительное «Денежной единицей в Российской Федерации является рубль». В этом суждении мы утверждаем, что рубль является основной валютой Российской Федерации, другими словами, что в класс ве­щей, который мы обозна­чаем при помощи сказуе­мого «рубль», вхо­дит целиком класс ве­щей, обозначаемых подлежащим.

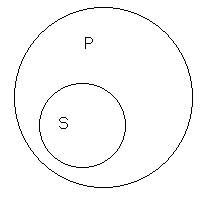
Если понятие S содержится в объеме поня­тия Р, то символически мы можем это представить при помощи круга S, который находится внутри круга Р. Поэтому те обще-утвердительные суждения, в которых объем подлежащего меньше объема сказуемого, можно символически изобразить, как это представлено на рисунке.

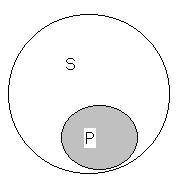
Суждения I. Возьмем частно-утвердительное суждение «Большинство студентов юридических вузов изучают конфликтологию». В этом суждении часть класса «S входит в объем класса Р, т. е. совпадает с классом Р. Если какая-нибудь часть S совпадает с Р, то круги S и Р должны иметь общую часть, т.е. должны пересекаться. Символически отношение между под­лежащим и сказуемым в частно-утвердительных суждениях можно изобразить так, как это сделано на рисунке. Та часть S, о которой утверждается в Р, на рисунке заштрихована.

3. Установите вид сложного суждения, укажите его составные части (простые суждения), запишите с помощью символов, используя пропозициональные союзы. Составьте таблицу истинности. Если сложное суждение комбинированное, приведите его полную логическую схему.

3.1. «Равенство может быть правом, но никакая человеческая сила не в состоянии обратить его в факт» (О. Бальзак).

Данное суждение является сложным, т.к. здесь отрицается простое суждение. Сложные суждения всегда могут быть сведены к простым.

Обозначим составные части данного суждения: Равенство может быть правом; Никакая человеческая сила не в состоянии обратить равенство в факт.

Символически это суждения выражаются формулой

«в R с»,

что читается как «в и с находятся в отношении R».

3.2. «Каждый имеет право на участие в культурной жизни и пользование учреждениями культуры, на доступ к культурным ценностям» (Конституция РФ).

Поскольку данное суждение состоит из двух частей и соединено союзом «и», оно является сложным.

Данное сложное суждение состоит из двух простых: Каждый имеет право на участие в культурной жизни; Каждый имеет право на доступ к культурным ценностям.

С помощью символов данное суждение можно записать так:

«Каждый S есть Р».

4. Нарисуйте логический квадрат, напишите виды отношений между суждениями в логическом квадрате и установите истинность других суждений, если исходные суждения следующие:

А. «Есть еще порох в пороховницах» – истинно;

Б. «Реформу нравов следует начинать с реформы законов» – ложно.

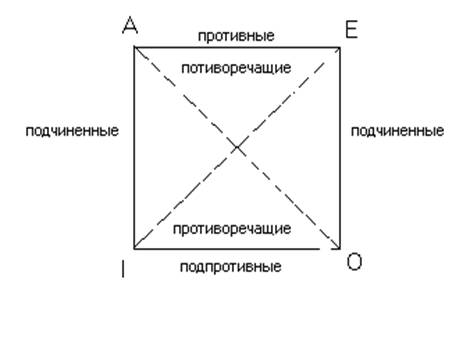
Схема эта наглядно показывает взаимное отношение суждений всех четырех классов.

Возьмем квадрат и проведем в нем диагонали. У вершин четырех его углов поставим буквы А, Е, I, О, т.е. символы четырех классов суждений. Возьмем какое-нибудь суждение и представим его в формах суждений всех четырех классов: А - «все люди честны», Е - «ни один человек не честен», I - «некоторые люди честны», О - «некоторые люди не суть честны».

Между суждениями А и О, Е и I существует отношение, которое называется «противоречием». Эти суждения отличаются и во количеству и по качеству.

Отношение между А и Е называется противностью. Эти общие суждения отличаются друг от друга по качеству.

Между А и I, Е и О есть отношения подчинения. Здесь сужде­ния отличаются по количеству.

Между I и О - отношение подпротивности. Здесь два част­ных суждения отличаются по качеству.

Рассмотрим каждую пару этих суждений в отдельности.

Противоречие (А - О, Е - I). Высказываем суждение А - «есть еще порох во всех пороховницах». Вы находите, что это суждение ложно. В таком случае вы должны признать истинным суждение О - «в некоторых пороховницах есть еще порох». Если вы не допустите истин­ности этого последнего суждения, то вы не можете признать лож­ности суждения А. Следовательно, при ложности суждения А, суждение О должно быть истинным.

Возьмем суждение О - «реформу нравов следует начинать с реформы законов». Это суждение мы должны признать ложным, потому что мы признаем- истинным суждение А - «реформу нравов не следует начинать с реформы законов». Сле­довательно, при ложности О суждение А - истинно[2].

Таким образом, из двух противоречащих суждений при истин­ности одного суждения другое оказывается ложным, при лож­ности одного суждения другое является истинным. Из этого сле­дует, что из противоречащих суждений одно должно быть ис­тинным, а другое - ложным. Два противоречащих суждения не могут быть в одно и то же время оба истинными, но не могут быть и оба ложными.

5. Сделайте полный разбор силлогизма. Если  заключение с необходимостью не следует, укажите, какие правила нарушены.

5.1. Мошенничество – преступление, а поскольку все преступления наказуемы, то мошенничество наказуемо.

Посылки силлогизма пишутся, как правило, одна над другой и отделяются горизонтальной чертой от заключения.

Мошенничество – преступление

Все преступления наказуемы

____________________________

Мошенничество наказуемо

Весь силлогизм в символической записи выглядит следующим образом:

С есть В

Все В есть А

____________

С есть А

Порядок посылок в силлогизме несущественен, так же, как и несущественно, каким термином – А или – С обозначается субъект заключения.

В данном случае заключение с необходимостью следует.

5.2. Все мы, друзья, простудились. Тому, кто простужен, нельзя петь. Всем нам нельзя петь.

Запишем посылки силлогизма:

Все мы простужены

Простуженным нельзя петь

_________________________

Всем нам нельзя петь

Весь силлогизм в символической записи выглядит следующим образом:

А есть В

В не есть С

__________

А не есть С

Если понятие S содержится в объеме поня­тия Р, то символически мы можем это представить при помощи круга S, который находится внутри круга Р. Поэтому те обще-утвердительные суждения, в которых объем подлежащего меньше объема сказуемого, можно символически изобразить, как это представлено на рисунке.

6. Приведите логическую схему, установите истинность и логическую корректность следующих умозаключений, В индуктивных умозаключениях определите степень вероятности логического вывода.

В действительности существует только индуктивное умозаключение, которое является в двух формах, или 1) как заключение от частного к общему, которое и называется собственно индукцией, или 2) как заключение от част­ных к частным. Мы можем заключать от частных к частным или прямо, или не прямо, через посредство общего предложения. Этот второй случай и представляет собой дедукцию. Таким об­разом, умозаключение от частных к частным, но через по­средство общего составляет дедукцию[3].

6.1. «Если я стану хвалить женщин, то скажут, что я их не знаю. Если стану их хулить, то скажут, что они наставляют мне нос. Но это не мешает мне говорить о них хорошее или дурное». Следовательно

Данное умозаключение является индуктивным. В процессе индуктивного умозаключения мы умозаключаем от случаев, которые мы наблюдали и исследовали, к случаям, которых мы не наблюдали и не исследовали. Далее, вследствие того, что в процессе индукции мы от на­блюдения части класса умозаключаем ко всему классу, ин­дукция есть умозаключение от частного к общему, или умозаключение от менее общего к более общему.

Если мы имеем случаи наблюдать многократное повторение сходных явлений, то начинаем думать, что эти явления всегда бу­дут иметь место, если только мы не имели случая на­блюдать явлений, противоречащих им. Такая индукция называется популярной.

6.2. «Вам не кажется, что эту планету (Торманс) уже нельзя поднять из инферно? Что болезнь зашла слишком далеко, отравив людей испорченной наследственностью – дисгенетикой? Что люди Торманса уже не способны ни во что и заботятся лишь об элементарных удовольствиях, ради которых они готовы на все? Если на планете бродят одичалые толпы, если пустыни наступают, съедая плодородные почвы, если израсходованы минеральные богатства, если деградация во всем и особенно в душах людей, то чем, какой силой они поднимутся?» Следовательно

От популярной индукции отличается индукция научная. В этом процессе исследуют каждый отдельный наблюдаемый случай, анализируют его, все случайное для данного явления отбрасывают, ищут существенные признаки его и строят заклю­чения, приводя в связь и согласие эти последние с другими обоб­щениями. Такие выводы только и могут иметь характер более или менее достоверный[4].

Список литературы

1.                 Гетманов А.Д. Логика. М.: Мысль, 1986.

2.                 Горский Д.П. Логика. М.: Наука, 1963.

3.                 Кириллов В.И. Старченко А.А. Логика. М.: Знание, 1987.

4.                 Светлов В.А. Практическая логика: Учебное пособие. СПб: ИД «МиМ», 1997.

5.                 Челпанов Г.И, Учебник логики. М.: Новый Юрист, 2002.

[1] Горский Д.П. Логика. М.: Наука, 1963. С. 201.

[2] Гетманов А.Д. Логика. М.: Мысль, 1986. С. 109.

[3] Кириллов В.И. Старченко А.А. Логика. М.: Знание, 1987. С. 211.

[4] Челпанов Г.И, Учебник логики. М.: Новый Юрист, 2002. С. 105.