Содержание
Задача
1. 2
Задача
2. 3
Задача
3. 6
Литература. 9
Задача 1
Компания,
занимающаяся сбором компьютеров из поставляемых микросхем, начала в 2004 г.
выпуск компьютеров нового типа, продажа которых проводилась неравномерно, и
часть компьютеров пополнила запасы готовой продукции. Предположим, что в 2004
г. компанией было произведено 4 таких компьютера. Но, хотя они являются
абсолютно идентичными, затраты на каждый из них из-за роста цен на
комплектующие и затраты труда неодинаковы:
|
Номер единицы
|
1
|
2
|
3
|
4
|
Всего
|
|
Затраты,
тыс.руб.
|
500
|
550
|
600
|
650
|
2300
|
Предположим, что в действительности были
проданы единицы 1 и 3.
1)
Рассчитайте себестоимость реализованной продукции и
стоимость запасов при помощи четырех методов.
2)
Какой метод дает заниженную оценку налогооблагаемой
прибыли?
3)
Как изменятся результаты в период дефляции?
Постоянного уровня цен?
Решение:
1)
По методу индивидуальной оценки: себестоимость
реализованной продукции составит 500+600=1100 тыс.руб., стоимость запасов на
конец года будет равна 2300 – 1100=1200 руб.
По
методу средней себестоимости: средняя стоимость единицы запасов равна 2300/4=575 тыс.руб., себестоимость
реализованной продукции составит 575*2=1150 тыс.руб., стоимость запасов –
2300-1150=1150 тыс.руб.
По
методу LIFO: себестоимость
реализованной продукции равна 600+650=1250, стоимость запасов на конец года
будет 2300-1250=1050
По
методу FIFO: себестоимость
реализованной продукции составит 500+550=1050, стоимость запасов на конец года
будет 2300-1050=1250
2)
Заниженную оценку налогооблагаемой прибыли дает метод LIFO. Чтобы показать это,
возьмем выручку от реализации в целом 3000 тыс. руб. и составим таблицу:
|
Метод
оценки
|
Выручка
от реализации
|
Затраты
на реализованную продукцию
|
Отражаемая
в прибыли отчетность
|
Стоимость
запасов на конец года
|
|
Индивидуальная
|
3000
|
1100
|
1900
|
1200
|
|
FIFO
|
3000
|
1050
|
1950
|
1250
|
|
LIFO
|
3000
|
1250
|
1750
|
1050
|
|
Средней
себестоимости
|
3000
|
1150
|
1850
|
1150
|
Из
таблицы видно, что самые высокие затраты – по методу LIFO, поэтому налогооблагаемая прибыль меньше, чем при использовании
других методов.
Задача 2
Финансовый
менеджер компьютерной компании оценивает используемые методы контроля запасов
на примере одной из приобретаемых микросхем. Затраты на приобретение составляют
200 руб., кроме того за каждый заказ компании приходится платить поставщику
дополнительно 1000 руб. Минимальный размер заказа – 250 ед., годовая
прогнозируемая потребность в микросхемах – 5000 ед., а годовые затраты по
хранению данного вида запасов – около 20% их средней стоимости.
1)
Определите величину EOQ применительно к запасам микросхем.
2)
Определите величину общих затрат по поддержанию
запасов при размере заказываемой партии, равном EOQ.
3)
Каковы будут дополнительные затраты, если размер
одного заказа составит 400 ед. по сравнению с затратами на заказ, равный EOQ? 600 ед.?
4)
Предположим, поставщикам требуется две недели для
наладки оборудования, производства и контроля качества микросхем, а также
доставки их на завод компании. При условии, что время доставки одной партии и
расход запасов точно известны, определите, при достижении какого объема запасов
необходимо разместить новый заказ (в году 52 недели, а величина одного заказа
равна EOQ)?
5)
Поскольку существует неопределенность относительно
срока доставки и предстоящего расхода запасов, компании приходится поддерживать
страховой запас. Если страховой запас установлен на уровне 200 ед., как это
отразится на величине общих затрат по поддержанию запасов? Как изменится момент
размещения заказа? Какую защиту на случай увеличения потребления или задержки
поставки новой партии обеспечивает страховой запас?
6)
Предположим, фирма- поставщик предложила компании
скидку в размере 1% в случае, если размер заказа составит 1000 ед. и более.
Следует ли компании воспользоваться скидкой или нет? Почему?
7)
У большинства фирм расход запасов в течение года
происходит неравномерно, т.е. колеблется в зависимости от сезона. Может ли в
этом случае использоваться модель EOQ? Если да,
то каким образом?
Решение:
1)
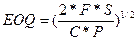 . В данном случае S= 5000
единиц, P= 200 руб.,
C= 20%, F= 1000 руб.
Таким образом
. В данном случае S= 5000
единиц, P= 200 руб.,
C= 20%, F= 1000 руб.
Таким образом 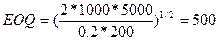 единиц.
единиц.
2)
Величину общих затрат по поддержанию запасов можно
рассчитать следующим образом: 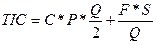 . Здесь Q= EOQ=500 единиц.
. Здесь Q= EOQ=500 единиц. 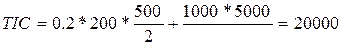 руб.
руб.
3)
При Q=400: 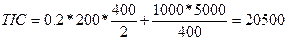 . Дополнительные затраты равны 500 рублей.
Q=600:
. Дополнительные затраты равны 500 рублей.
Q=600: 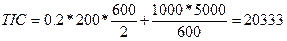 . Дополнительные затраты равны 333 рубля.
. Дополнительные затраты равны 333 рубля.
4)
В неделю
реализуется 5000/52=96 единиц. Если поставщикам требуется две недели для
доставки товара, то размещение заказа необходимо, когда запас достигнет 2*96=
192 шт. Еженедельно остаток запасов будет уменьшаться на 96 единиц и достигнет
нулевого уровня к моменту поступления новой партии.
5)
Страховой запас равен 200 единиц. Тогда средний запас
равен 500/2 + 200 = 450 ед., а средняя стоимость запасов равна 450*200=90000
руб. Увеличение объема среднего запаса ведет к увеличению затрат по хранению
запасов на 200*0,2*200=8000 руб. Момент размещения заказа наступит, когда
уровень запасов достигнет величины страхового запаса, т.е. 200 ед. Страховой запас
обеспечивает защиту на случай увеличения потребления или задержки поставки
новой партии, так как позволяет фирме не останавливать деятельность, а
реализовывать имеющуюся в этом запасе продукцию. Если
фирма предполагает, что возможно увеличение потребления, например, до
200 единиц в неделю, то в этом случае заказ будет возобновлен при уровне
запасов в 400 единиц. При задержке поставки страховой запас в 200 ед.
обеспечивает реализацию продукции в течение двух недель (т.к. в неделю
реализуется 96 ед.)
6)
Скидка 1% при размере заказа 1000 ед. общие затраты по
поддержанию запасов будут следующими: 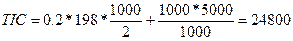 , что выше, чем при размере заказа, равном EOQ. Экономия от разницы цен равна 0,01*200= 2 рубля на
единицу. За год экономия 5000*2=10000 рублей. Чистая экономия равна
10000-4800=5200 рублей, поэтому
фирме следует воспользоваться скидкой.
, что выше, чем при размере заказа, равном EOQ. Экономия от разницы цен равна 0,01*200= 2 рубля на
единицу. За год экономия 5000*2=10000 рублей. Чистая экономия равна
10000-4800=5200 рублей, поэтому
фирме следует воспользоваться скидкой.
7)
В этом случае модель может использоваться в измененном
виде: оптимальная партия заказа будет рассчитываться отдельно для каждого
сезона. При этом необходимо использовать данные, скорректированные на
длительность сезона, а не годовые (т.е. сезонные потребность в запасах и
затраты по хранению).
Задача 3
У фирмы имеется свыше 20
тысяч видов запасов, необходимых для ремонта и обслуживания небольших
самолетов, одним из которых являются особые заклепки из титанового сплава.
Заклепки заказываются ежемесячно, т.е.цикл данного вида запасов равен 30 дням.
С момента размещения заказа на заклепки до его получения проходит 3 дня.
Ожидаемый 3- дневный расход данного вида запасов
составляет 1000 ед., но может быть как выше, так и ниже этой величины в
зависимости от типов самолетов, нуждающихся в ремонте. Распределение
вероятностей потребности в заклепках в течение трех дней представлены ниже
|
Вероятность
|
0,05
|
0,2
|
0,5
|
0,2
|
0,05
|
|
Необходимое
количество, ед.
|
0
|
500
|
1000
|
1500
|
2000
|
Прим.
Здесь вероятность для 500 ед. и 1500 ед. взята 0,2, поскольку сумма
вероятностей должна быть равна 1.
В случае нехватки запасов потери фирмы за
время простоя составят 50 руб. с одной единицы запасов. Компания рассматривает
варианты установления страхового запаса на уровне 0, 500 или 1000 заклепок.
Стоимость одной заклепки 500 рублей, а годовые затраты по хранению составляют
20% стоимости запасов.
Определите
оптимальный размер страхового запаса.
Решение:
Затраты
по хранению 1 единицы в год составляют 500*0,2=100 руб., затраты по хранению 1
ед. в месяц 100/12= 8,33 рублей.
|
Страховой
запас, ед.
|
Объем
реализации в течение времени исполнения заказа, ед.
|
Вероятность
|
Дефицит,
ед.
|
Потери
прибыли в связи с нехваткой запасов, руб.(50 р.*дефицит)
|
Ожидаемые
потери, руб.(потери прибыли*вероятность)
|
Затраты
по хранению страхового запаса, руб.(8,33*страховой запас)
|
Ожидаемые
общие затраты,руб.(ожидаемыепотери+
затраты по хранению страхового запаса)
|
|
|
|
|
|
|
|
|
|
|
0
|
0
|
0,05
|
0
|
0
|
0
|
0
|
7500
|
|
500
|
0,2
|
0
|
0
|
0
|
|
1000
|
0,5
|
0
|
0
|
0
|
|
1500
|
0,2
|
500
|
25000
|
5000
|
|
2000
|
0,05
|
1000
|
50000
|
2500
|
|
500
|
0
|
0,05
|
0
|
0
|
0
|
4165
|
4190
|
|
500
|
0,2
|
0
|
0
|
0
|
|
1000
|
0,5
|
0
|
0
|
0
|
|
1500
|
0,2
|
0
|
0
|
0
|
|
2000
|
0,05
|
500
|
25000
|
25
|
|
1000
|
0
|
0,05
|
0
|
0
|
0
|
8330
|
8330
|
|
500
|
0,2
|
0
|
0
|
0
|
|
1000
|
0,5
|
0
|
0
|
0
|
|
1500
|
0,2
|
0
|
0
|
0
|
|
2000
|
0,05
|
0
|
0
|
0
|
Ожидаемые
общие затраты минимальны при страховом запасе в 500 единиц, поэтому этот размер
– оптимальный для страхового запаса.
Литература
1.
Бригхем Ю.
Финансовый менеджмент, т.1. СПб, ВШЭ, 2000- 497
2.
Бригхем Ю. Финансовый менеджмент, т.2. СПб, ВШЭ, 2000- 669
3.
Волков О.И. Экономика предприятия (фирмы). 2002, М., Инфра-М – 900с.
4.
М.В. Романовский. Финансы. М.,Юрайт,2002 – 502с.
5.
М.В. Романовский. Финансы предприятий. СПб,
Бизнес-пресс,2000 – 528с.