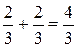Вариант 1.
Задание 1.
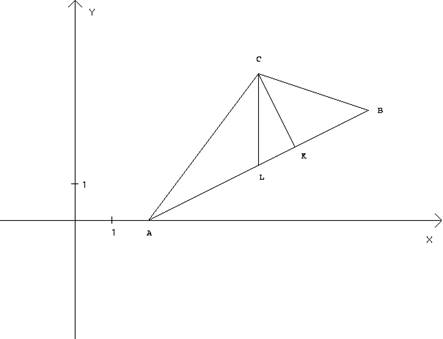
Дан треугольник ABC: A(2,0),
B(8,3), C(5,4). Найти:
1) длину стороны AB;
2) внутренний угол A с точностью до градуса;
3) уравнение и длину высоты, опущенной из вершины С;
4) точку пересечения высот;
5) уравнение медианы, проведенной через вершину C;
6) систему линейных неравенств, определяющих треугольник ABC.
Сделать чертеж.
Решение.
1) Длина стороны AB.
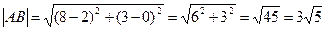
2) внутренний угол A с точностью до градуса;
Найдем длины сторон
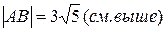
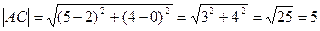
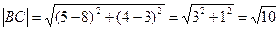
Найдем угол A по теореме косинусов.
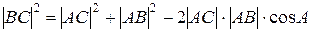
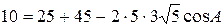
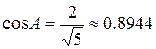
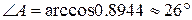
3) уравнение и длину высоты, опущенной из вершины С;
Найдем уравнение стороны AB.
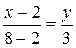
3x–6=6y
3x–6y–6=0
x–2y–2=0
Общее уравнение перпендикуляра к этой прямой 2x+y+C1=0, где C1 – некоторая постоянная.
C1
найдем из условия, что прямая проходит через точку C.
10+4+C1=0
C1=–14
Искомое уравнение 2x+y–14=0
Точка пересечения
стороны AB и высоты, опущенной из точки C.
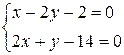
x=2y+2
4y+4+y–14=0
5y=10
y=2
x=6
Точка пересечения K(6;2).
Длина высоты CK.
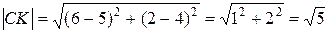
4) точку пересечения высот.
Для нахождения точки пересечения высот найдем высоту, проходящую
через точку A.
Уравнение стороны BC.
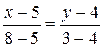
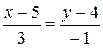
–x+5=3y–12
x+3y–17=0
Уравнение перпендикуляра к стороне BC 3x–y+C1=0. C1
найдем из условия, что эта прямая проходит через точку A.
6–0+C1=0
C1=–6
Уравнение высоты, проходящей через точку A – 3x–y–6=0
Точка пересечения высот.
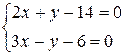
5x–20=0
x=4
8+y–14=0
y=6
H(4;6)
– точка пересечения высот.
5) уравнение медианы, проведенной через вершину C;
Найдем середину стороны АВ
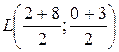
L(5;1.5)
Уравнение медианы найдем из условия, что она проходит через
точки C и L.
x–5=0
6) систему линейных неравенств, определяющих треугольник ABC.
Уравнение стороны AB: x–2y–2=0
Уравнение стороны BC: x+3y–17=0
Уравнение стороны AC:
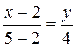
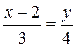
4x–8=3y
4x–3y–8=0
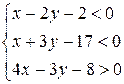
Задание 2.
Даны векторы a1(–1,–2,0,1),
a2(2,
1,-1,2), a3(–1,–1,-1,3),
a4(1,0,–2,0),
b(–4,–4,4,–3). Доказать,
что векторы a1,
a2, a3, a4 образуют базис
четырехмерного пространства и найти координаты вектора b в этом базисе.
Найдем определитель матрицы со столбцами, состоящими из
координат векторов.
~ 
= 
= 
~ 
= 
= 
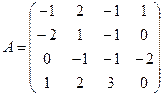
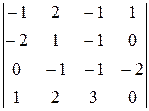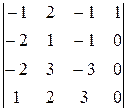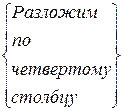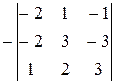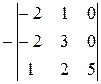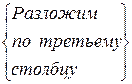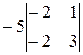= 20≠0, следовательно
вектора линейно независимы и образуют базис четырехмерного пространства. Найдем
координаты вектора b в этом базисе.
Обозначим искомые координаты x1,x2,x3,x4.
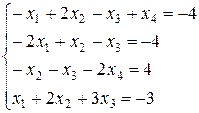
x1=2x2–x3+x4+4
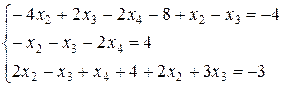
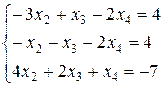
x2=–x3–2x4–4
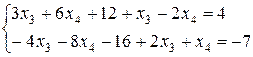
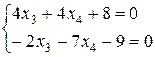
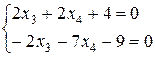
–5x4–5=0
x4=–1
x3=–1
x2=1+2–4=–1
x1=–2+1–1+4=2
В итоге получили разложение:
b=2a1–a2–a3–a4
Задание 3.
Найти производные функций:
а)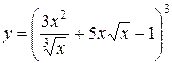 
= 
= 
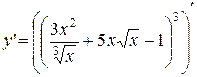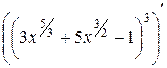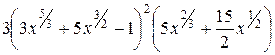
б) y=ln tg(3x)
= 
= 
= 
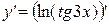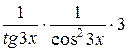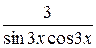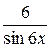
в)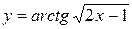 
= 
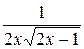
г)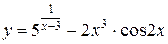 
= 
= 
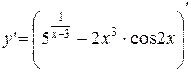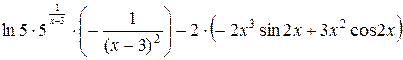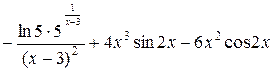
Задание 4.
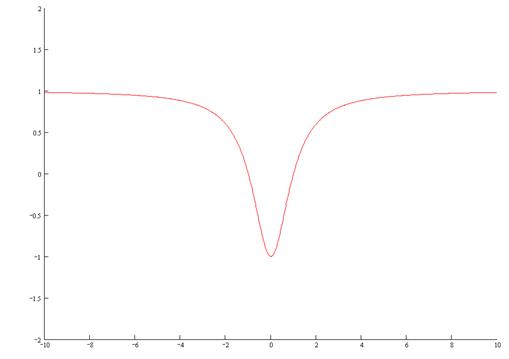
Исследовать функцию и построить ее график.
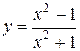
1. Областью определения функции является вся числовая
прямая.
2. 
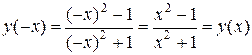, функция четна.
3. y(0)=–1
y(x)=0 при x=–1;1
4. Т.к. функция непрерывна в области определения, то
вертикальных асимптот нет.
Найдем невертикальные асимптоты, если они существуют.
y=kx+b
= 
= 
∙ 
= 
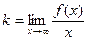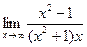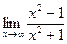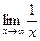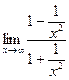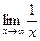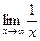∙ = = 0
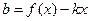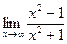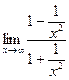= = = 1
y=1 – горизонтальная
асимптота.
4. 
= 
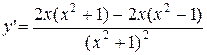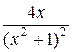
y’=0
при x=0
|
x
|
(–∞;0)
|
0
|
(0;+∞)
|
|
y'
|
–
|
0
|
+
|
|
y
|
убывает
|
мин.
y(0)=–1
|
возрастает
|
5. 
= 
= 
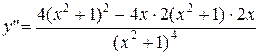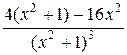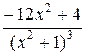
y”=0
12x2=4
|
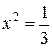
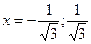
x
|
(–∞; )
|
|
(; )
|
|
(;+∞)
|
|
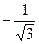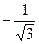
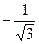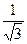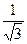
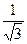y"
|
–
|
0
|
+
|
0
|
–
|
|
y
|
выпукла
|
–0.5
т.
перегиба
|
вогнута
|
–0.5
т.
перегиба
|
выпукла
|
Задание 5.
«Неопределенный интеграл»
а) Применяя таблицу интегралов и метод замены переменных
найти неопределенные интегралы. Результаты проверить дифференцированием.
= 
= 
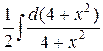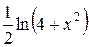
Проверка.
= 
= 
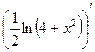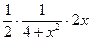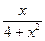
б) Применяя таблицу интегралов и метод замены переменных
найти неопределенные интегралы. Результаты проверить дифференцированием.
= 
= 
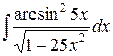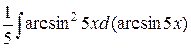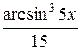
Проверка.
= 
= 
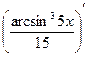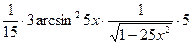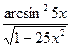
в) Применяя метод интегрирования по частям найти
неопределенные интегралы. Результаты проверить дифференцированием.
= 
= 
= 
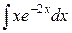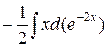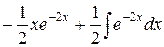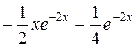
Проверка.
= 
= 
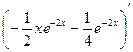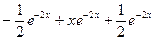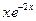
г) Применяя метод интегрирования рациональных функций, найти
неопределенные интегралы. Результаты проверить дифференцированием.
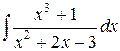
Преобразуем подынтегральное выражение.
x3+1=(x2+2x–3)(x–2)+7x–5
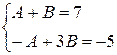
4B=2
В=0.5
A=6.5
= 
= 
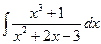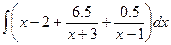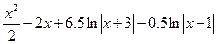
Проверка.
= 
= 
= 
= 
= 
= 
= 
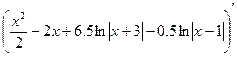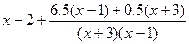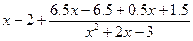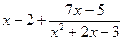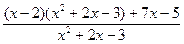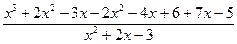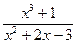
Задание 6.
Вычислить площадь фигуры, ограниченной графиками функций y=f1(x), y=f2(x), где f1(x)=–x2+x+1,
f2(x)=–2x2+x+2.
Найдем точки пересечения графиков.
–x2+x+1=–2x2+x+2
x2–1=0
x=–1;1
Следовательно, искомая площадь равна
= 
= 
= 
= 
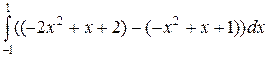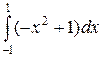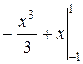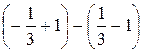