- Исследование структуры совокупности.
1. Строим статистический ряд
распределения предприятий по признаку среднегодовая
стоимость основных производственных
фондов, образовав пять групп с равными интервалами.
Величина интервала определяется по
формуле:
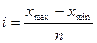 , где n – число групп.
, где n – число групп.
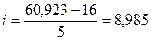
Таблица 1. Ряд распределения
предприятий по среднегодовой стоимости
основных производственных фондов.
|
Группы
предприятий по среднегодовой стоимости основных производственных фондов, млн.
руб.
|
Число
пред-приятий
|
Центр
интервала, млн. руб.
|
Накоп-ленные
частоты
|
|
|
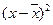
|
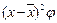
|
|
16
– 24,985
|
3
|
20,493
|
3
|
61,479
|
-19,467
|
378,964
|
1136,892
|
|
24,985
– 33,97
|
4
|
29,478
|
7
|
117,912
|
-10,782
|
116,251
|
465,004
|
|
33,97
– 42,955
|
12
|
38,463
|
19
|
461,556
|
-1,497
|
2,241
|
26,892
|
|
42,955
– 51,94
|
7
|
47,448
|
26
|
332,136
|
7,488
|
56,07
|
392,49
|
|
51,94
- -60,925
|
4
|
56,433
|
30
|
225,728
|
16,473
|
271,36
|
1085,44
|
|
Всего
|
30
|
|
|
1198,811
|
|
824,886
|
3106,718
|
1.2.Строим
графики полученного ряда распределения.
Графически определяем значения моды и медианы.
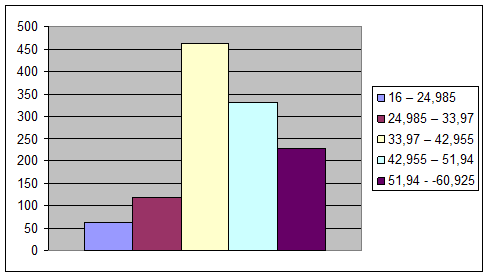
Рис. 1. Гистограмма распределения предприятий по среднегодовой
стоимости основных производственных фондов.
Для определения моды графическим
способом на гистограмме распределения правую вершину модального прямоугольника
соединяют с правым верхним углом предыдущего прямоугольника, а левую вершину
модального прямоугольника – с левым верхним углом последующего прямоугольника.
Абсцисса точки пересечения этих прямых будет модой распределения.
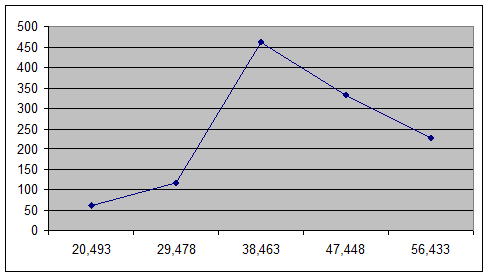
Рис. 2. Полигон распределения
предприятий по среднегодовой стоимости основных производственных фондов.
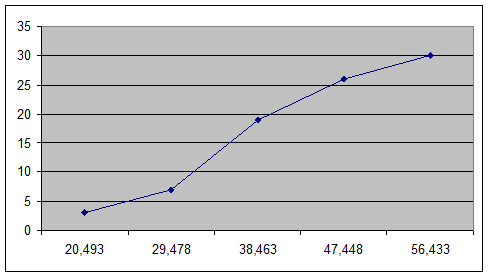
Рис. 3. Кумулята распределения
предприятий по среднегодовой стоимости основных производственных фондов.
Для определения медианы графическим
способом высоту наибольшей ординаты кумуляты, которая соответствует общей
численности, делят пополам. Через полученную точку проводят прямую,
параллельную оси абсцисс до пересечения ее с кумулятой. Абсцисса точки
пересечения является медианной величиной.
1.3.
Рассчитаем характеристики интервального ряда распределения: среднюю
арифметическую, среднее квадратическое отклонение, коэффициент вариации.
Средняя арифметическая (для
интервального ряда распределения рассчитывается по формуле средней
арифметической взвешенной):
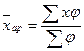
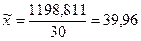 (млн. руб.)
(млн. руб.)
Среднее квадратическое отклонение:

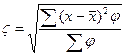
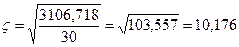 (млн. руб.)
(млн. руб.)
Коэффициент вариации:
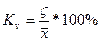
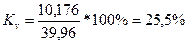
Вывод: Удельный вес среднего
квадратического отклонение в среднем значении составляет 25,5%. Так как
коэффициент вариации меньше 33.3%, то можно считать, что совокупность достаточно
однородна, а среднее для данной совокупности надежно.
4. Вычислим среднюю арифметическую
по исходным данным, сравним ее с аналогичным показателем, рассчитанным в пункте
3 для интервального ряда распределения. Объясним причину их расхождения.
Сделаем выводы по результатам
выполнения задания.
Средняя арифметическая простая:
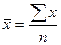
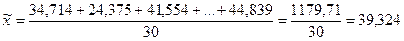 (млн. руб.)
(млн. руб.)
Вывод: Средняя арифметическая для интервального ряда (39,96 млн. руб.) и средняя арифметическая,
вычисленная по исходным данным (39,323 млн. руб.) различаются на 0,637 млн. рублей. Первый показатель является менее точным, так
как при его расчете учитывается количество предприятий, относящихся к
определенному интервалу, а это – приближение.
2.Выявление наличия корреляционной связи
между признаками, установление
направления связи и измерение её тесноты
По исходным данным:
1. 2.Установим наличие и характер
связи между признаками – среднегодовая стоимость производственных фондов и
выпуск продукции методами:
а) аналитической группировки;
б) корреляционной таблицы.
Решение:
а) Метод аналитической группировки
Таблица 2. Рабочая таблица
группировки предприятий по среднегодовой стоимости основных производственных
фондов.
|
Группы
предприятий по стоимости основных производственных фондов, млн. руб.
|
№
предприятия
п/п
|
Среднегодовая
стоимость основных производственных фондов, млн. руб.
|
Выпуск продукции,
млн. руб.
|
|
1
|
2
|
3
|
4
|
|
16
– 24,985
|
15
|
16
|
14,4
|
|
20
|
19,362
|
18,2
|
|
2
|
24,375
|
23,4
|
|
Итого
|
3
|
59,737
|
56
|
|
24,985
– 33,97
|
6
|
27,408
|
26,86
|
|
24
|
28,727
|
28,44
|
|
10
|
30,21
|
30,21
|
|
21
|
31,176
|
31,8
|
|
Итого
|
4
|
117,521
|
117,31
|
|
33,97
– 42,955
|
14
|
34,388
|
35,42
|
|
29
|
34,522
|
35,903
|
|
1
|
34,714
|
36,45
|
|
16
|
34,845
|
36,936
|
|
22
|
36,985
|
39,204
|
|
9
|
37,957
|
40,424
|
|
18
|
38,318
|
41
|
|
5
|
38,347
|
41,415
|
|
27
|
38,378
|
41,832
|
|
11
|
38,562
|
42,418
|
|
25
|
39,404
|
43,344
|
|
3
|
41,554
|
46,54
|
|
Итого
|
12
|
447,974
|
480,886
|
|
42,955
– 51,94
|
30
|
44,839
|
50,22
|
|
13
|
45,674
|
51,612
|
|
17
|
46,728
|
53,392
|
|
1
|
2
|
3
|
4
|
|
1
|
2
|
3
|
4
|
|
8
|
47,172
|
54,72
|
|
19
|
47,59
|
55,68
|
|
23
|
48,414
|
57,128
|
|
4
|
50,212
|
59,752
|
|
Итого
|
7
|
330,329
|
382,504
|
|
51,94
– 60,923
|
12
|
52,5
|
64,575
|
|
26
|
55,25
|
70,72
|
|
28
|
55,476
|
69,345
|
|
7
|
60,923
|
79,2
|
|
Итого
|
4
|
224,149
|
283,84
|
|
Всего
|
30
|
1179,71
|
1320,54
|
Таблица 3. Сводная таблица
группировки предприятий по среднегодовой стоимости основных производственных
фондов.
|
Группы
предприятий по стоимости основных производственных фондов, млн. руб.
|
Число предприятий
|
Среднегодовая
стоимость основных производственных фондов, млн. руб.
|
Выпуск продукции,
млн. руб.
|
|
Всего
|
В среднем на одно
предприятие
|
Всего
|
В среднем на одно
предприятие
|
|
16
– 24,985
|
3
|
59,737
|
19,912
|
56
|
18,667
|
|
24,985
– 33,97
|
4
|
117,521
|
29,38
|
117,31
|
39,328
|
|
33,97
– 42,955
|
12
|
447,974
|
37,331
|
480,886
|
40,174
|
|
42,955
– 51,94
|
7
|
330,329
|
47,19
|
382,504
|
54,643
|
|
51,94
- -60,925
|
4
|
224,149
|
56,037
|
283,84
|
70,96
|
|
Всего
|
30
|
1179,71
|
37,97
|
1320,54
|
44,754
|
Вывод: Результаты группировки
показывают, что между среднегодовой стоимостью основных производственных фондов
и выпуском продукции существует прямая зависимость: увеличение стоимости
основных производственных фондов ведет к увеличению выпуска продукции в
целом и в среднем на одно предприятие.
б) Метод корреляционной таблицы
Для построения корреляционной
таблицы необходимо разбить предприятия по признаку выпуск продукции на пять
групп с равными интервалами.
Величина интервала составит:
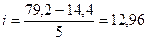 (млн. руб.)
(млн. руб.)
Получаем следующие пять групп: 14,4 -
27,36
27,36 – 40,32
40,32 – 53,28
53,28 – 66,24
66,24 – 79,2
Таблица 4. Корреляционная таблица.
|
Среднегодовая
стоимость основных производственных фондов, млн. руб.
|
Выпуск продукции,
млн. руб.
|
Итого
|
|
14,4 -
27,36
|
27,36 – 40,32
|
40,32 – 53,28
|
53,28 – 66,24
|
66,24 – 79,2
|
|
16
– 24,985
|
3
|
|
|
|
|
3
|
|
24,985
– 33,97
|
1
|
3
|
|
|
|
4
|
|
33,97
– 42,955
|
|
5
|
7
|
|
|
12
|
|
42,955
– 51,94
|
|
|
2
|
5
|
|
7
|
|
51,94
- -60,925
|
|
|
|
1
|
3
|
4
|
|
Итого
|
4
|
8
|
9
|
6
|
3
|
30
|
Вывод: Анализ таблицы показывает, что частоты расположены по
диагонали сверху вниз, что свидетельствует о наличии прямой связи между
среднегодовой стоимостью основных производственных фондов и выпуском продукции.
Так как наблюдается концентрация частот вокруг главной диагонали и незаполненность
оставшихся клеток, то можно предположить достаточно тесную связь между
рассматриваемыми признаками.
2.2. Измерим тесноту корреляционной
связи между названными признаками с использованием коэффициентов детерминации и
эмпирического корреляционного отношения.
Сделайем выводы по результатам
выполнения задания.
Решение:
Коэффициент детерминации:
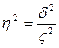 ,
,
где 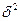 – межгрупповая
дисперсия,
– межгрупповая
дисперсия,
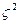 – дисперсия.
– дисперсия.
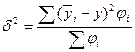
Таблица 5. Расчет межгрупповой
дисперсии.
|
Среднегодовая
стоимость основных производственных фондов, млн. руб.
|
Число предприятий
|
Выпуск продукции,
млн. руб.
|
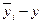
|
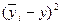
|
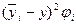
|
|
16
– 24,985
|
3
|
18,667
|
-26,087
|
680,532
|
2041,596
|
|
24,985
– 33,97
|
4
|
39,328
|
-5,426
|
29,441
|
117,764
|
|
33,97
– 42,955
|
12
|
40,174
|
-4,58
|
20,976
|
251,712
|
|
42,955
– 51,94
|
7
|
54,643
|
9,889
|
97,792
|
684,544
|
|
51,94
- -60,925
|
4
|
70,96
|
26,206
|
686,754
|
2747,016
|
|
Всего
|
30
|
44,754
|
|
|
5842,632
|
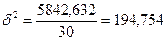 (млн. руб.)
(млн. руб.)
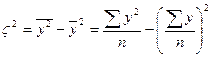
Таблица 6. Расчет общей дисперсии.
|
№
предприятия
|
Выпуск продукции,
млн. руб. (у)
|
У2
|
|
1
|
2
|
3
|
|
1
|
14,4
|
207,36
|
|
2
|
18,2
|
331,24
|
|
3
|
23,4
|
547,56
|
|
4
|
26,86
|
721,46
|
|
5
|
28,44
|
808,834
|
|
6
|
30,21
|
912,644
|
|
7
|
31,8
|
1011,24
|
|
8
|
35,42
|
1254,576
|
|
9
|
35,903
|
1289,025
|
|
10
|
36,45
|
1328,603
|
|
11
|
36,936
|
1364,268
|
|
12
|
39,204
|
1536,953
|
|
13
|
40,424
|
1634,1
|
|
14
|
41
|
1681
|
|
15
|
41,415
|
1715,202
|
|
16
|
41,832
|
1749,916
|
|
17
|
42,418
|
1799,287
|
|
18
|
43,344
|
1878,702
|
|
19
|
46,54
|
2165,971
|
|
20
|
50,22
|
2522,048
|
|
21
|
51,612
|
2663,799
|
|
22
|
53,392
|
2850,706
|
|
23
|
54,72
|
2994,278
|
|
24
|
55,68
|
3100,262
|
|
1
|
2
|
3
|
|
25
|
57,128
|
3263,608
|
|
26
|
59,752
|
3570,301
|
|
27
|
64,575
|
4169,931
|
|
28
|
70,72
|
5001,318
|
|
29
|
69,345
|
4808,729
|
|
30
|
79,2
|
6272,64
|
|
Всего
|
1320,54
|
65155,561
|
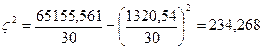 (млн. руб.)
(млн. руб.)
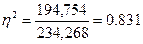
Эмпирическое корреляционное отношение:
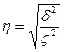
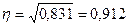
Вывод: Вариация выпуска продукции на 83,1 % обусловлена вариацией
стоимости основных производственных фондов. Для качественной оценки тесноты
связи воспользуемся шкалой Чэддока. Согласно этой шкале при значении
эмпирического корреляционного отношения 0,912 можно говорить о наличии между
рассматриваемыми признаками весьма тесной зависимости.
3.Применение выборочного
метода в финансово-экономических задачах.
По результатам выполнения задания 1
с вероятностью 0,683 определите:
1. Ошибку выборки средней стоимости
основных производственных фондов и границы, в которых будет находиться средняя
стоимость ОПФ в генеральной совокупности.
Решение:
Среднегодовая стоимость основных
производственных фондов составляет 39,324 млн. руб. Оценим величину ошибки
выборки при определении среднего значения:
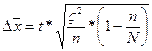 ,
,
где 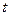 – коэффициент доверия
(при заданной доверительной вероятности 0,683
– коэффициент доверия
(при заданной доверительной вероятности 0,683 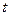 =1);
=1);
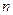 – размер выборочной совокупности;
– размер выборочной совокупности;
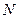 – размер генеральной
совокупности.
– размер генеральной
совокупности.
Для 20 % механической выборки 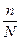 =0,8.
=0,8.
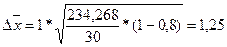 (млн. руб.)
(млн. руб.)
39,324 – 1,25 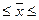 39,324 + 1,25
39,324 + 1,25
38,074 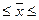 40,574
40,574
Вывод: с вероятностью 0.683 можно утверждать, что среднегодовая
стоимость основных производственных фондов в среднем на одно предприятие в
генеральной совокупности будет лежать в пределах от 38,074 млн. рублей до 40,574 млн. рублей. Эти пределы распространяются на
683 единицы из 1000.
2. Ошибку выборки доли предприятий
со среднегодовой стоимостью основных производственных фондов 43 млн. руб. и
более и границы, в которых будет находиться генеральная доля.
Решение:
В выборочной совокупности доля
предприятий со среднегодовой стоимостью основных производственных фондов
составляет:
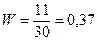 (или 37 %)
(или 37 %)
Ошибка выборки для доли признака:
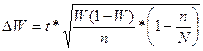
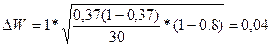 (или 4 %)
(или 4 %)
37 – 4 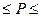 37 + 4
37 + 4
33 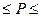 41
41
Вывод: С вероятностью 0.683 можно утверждать, что доля предприятий
со среднегодовой стоимостью основных производственных фондов 43 млн. рублей и
выше находится в пределах от 33 % до 41 %. Эти пределы распространяются на 683 единицы из 1000.
4.Использование одного из статистических методов в финансово-экономических задачах.
Имеются следующие данные по региону
об элементах экономических активов, включаемых в состав национального
богатства, млн. руб.:
|
Основные фонды
|
25500
|
|
Материальные оборотные средства
|
1900
|
|
Ценности
|
9000
|
|
Затраты на геологоразведку
|
600
|
|
Средства программного обеспечения
|
500
|
|
Оригиналы художественных и литературных произведений
|
15000
|
|
Земля
|
40000
|
|
Полезные ископаемые
|
48000
|
|
Лицензии, патенты, авторские права
|
2500
|
|
Монетарное золото
|
45000
|
|
Специальные права заимствования
|
8500
|
|
Денежная наличность
|
12000
|
|
Депозиты
|
380
|
|
Акции
|
11500
|
|
Займы
|
2200
|
Определите:
1. Объем нефинансовых и финансовых активов национального
богатства, а также их общий объем.
2. Показатели структуры нефинансовых активов, выделив
произведенные и не произведенные активы (представьте в таблице).
Сделайте выводы.
Решение:
Таблица 7. Распределение активов национального богатства по
типам.
|
Тип актива
|
Актив
|
Стоимость актива,
млн. руб.
|
|
Нефинансовые
активы
|
Произведенные
активы
|
Основные фонды
|
25500
|
|
Материальные оборотные средства
|
1900
|
|
Ценности
|
9000
|
|
Затраты на геологоразведку
|
600
|
|
Средства программного обеспечения
|
500
|
|
Оригиналы художественных и литературных произведений
|
15000
|
|
Произведенные
активы
|
52500
|
|
Непроизведенные
активы
|
Земля
|
40000
|
|
Полезные ископаемые
|
48000
|
|
Лицензии, патенты, авторские права
|
2500
|
|
Непроизведенные
активы
|
90500
|
|
Нефинансовые активы
|
143000
|
|
Финансовые
активы
|
Монетарное золото
|
45000
|
|
Специальные права заимствования
|
8500
|
|
Денежная наличность
|
12000
|
|
Депозиты
|
380
|
|
Акции
|
11500
|
|
Займы
|
2200
|
|
Финансовые активы
|
79580
|
|
Общий объем финансовых и нефинансовых
активов
|
222580
|
Общий объем финансовых и
нефинансовых активов составляет:
143000 + 79580 = 222580 (млн. руб.)
Показатели
структуры вычисляются как отношение стоимости одного вида активов к общей
стоимости нефинансовых активов:
для произведенных активов
52500/143000 = 0,367 (36,7 %),
для непроизведенных активов
90500/143000 = 0,633 (63,3 %).
Таблица 9. Показатели структуры нефинансовых активов.
|
Актив
|
Стоимость актива,
млн. руб.
|
|
Произведенные
активы
|
36,7%
|
|
Непроизведенные
активы
|
63,3%
|
|
Всего:
|
100 %
|
Вывод: общий объем финансовых и нефинансовых активов составляет 222
580 млн. рублей, из которых
143 000 млн. рублей
приходится на нефинансовые активы, а 79 580 млн. рублей – на финансовые. В
нефинансовых активах доля произведенных активов составляет 36,7%, а непроизведенных
– 63,3%.