МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
ФИЛИАЛ В Г. КАЛУГА
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ
По дисциплине
«Экономико-математические методы и прикладные модели»
Вариант №8
Исполнитель:
Косорукова А.Е.
Курс: 3 (вечер)
Специальность: Финансы и кредит
№ зачетной книжки: 07ФФД40888
Руководитель: Князева И.В.
КАЛУГА,
2008
Задача 1. Задача об оптимальном
использовании ограниченных ресурсов
Для
изготовления продукции четырех видов используется три вида оборудования. Затраты
на изготовление ед. продукции указаны в таблице:
|
Тип оборуд-ия
|
Нормы затрат рес. на ед. продук.
|
Общ. фонд раб. времени
|
|
А
|
Б
|
В
|
Г
|
|
Токарное
|
2
|
1
|
1
|
3
|
300
|
|
Фрезерное
|
1
|
0
|
2
|
1
|
70
|
|
Шлифовальное
|
1
|
2
|
1
|
0
|
340
|
|
Цена изделия
|
8
|
3
|
2
|
1
|
|
§ Как изменится общая стоимость выпускаемой продукции и
план ее выпуска, если фонд времени шлиф. Оборудования увеличить на 24 ч.?
§ Целесообразно ли выпускать изделие Д, ценой 11 ед.,
если нормы затрат оборудования составляют 8,2 и 2 ед.?
Решение:
1.
Создать форму
для ввода условий задачи. Запустить Excel. Открывается
чистый лист Excel. Создать текстовую форму-
таблицу для ввода условий задачи.
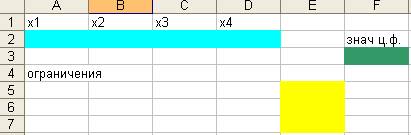
2.
Указать
адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки).
Обозначить для х1, х2, х3, х4 количество ресурсов каждого типа. Оптимальные
значения компонент вектора Х=(х1, х2, х3, х4) будут помещены в ячейках А3:Д3оптимальное значение целевой
функции в ячейке F3. Ввести исходные данные задачи в созданную
форму-таблицу:
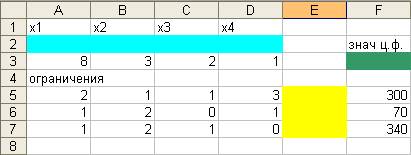
3.
Ввести
зависимость для целевой функции:
- курсор в ячейку F3
- курсор на кнопку «Мастер функций», расположенную на панели инструментов. На экране
появляется диалоговое окно Мастер
функций:
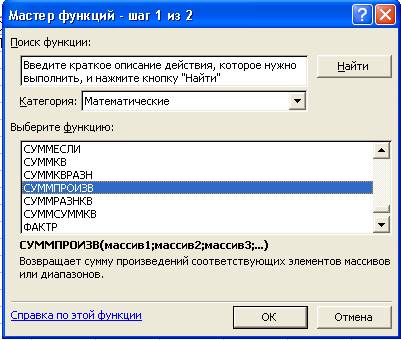
- курсор в окно «Категория»
и нажать на категорию «Математические»;
- в окне «Выберите
функцию» нажать на СУММПРОИЗВ;
- нажать кнопку ОК.
На экране появляется диалоговое окно СУММПРОИЗВ:
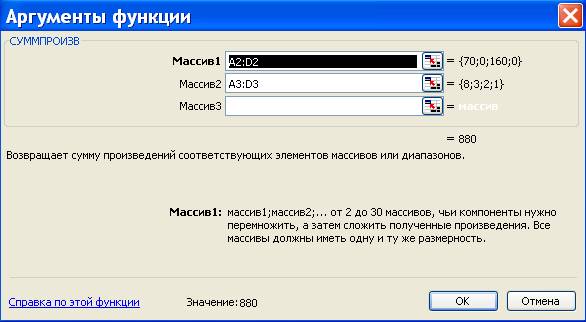
- копка «ОК». На экране в ячейку F3 введена
функция:
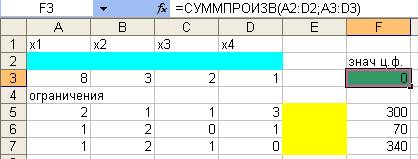
4. Ввести зависимость для ограничений:
- курсор в ячейку Е5.
- Нажать на кнопку «Мастер функций», выбрать в категории «Математические» функцию СУММПРОИЗВ;
- кнопка ОК.
- в строку «Массив
1» ввести А2:Д2;
- в строку «Массив
2» ввести А5:Д5;
- кнопка ОК.
- выполнить аналогичные действия относительно ячеек Е6
и Е7.
Получаем в результате в ячейки Е5-Е7 введены функции:
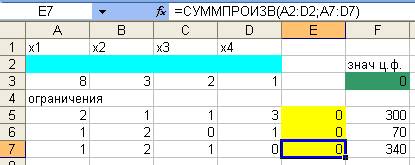
5. В строке Меню
указатель мыши на имя Сервис.
В развернутом меню команда Поиск решения. Появится диалоговое окно Поиск решения:
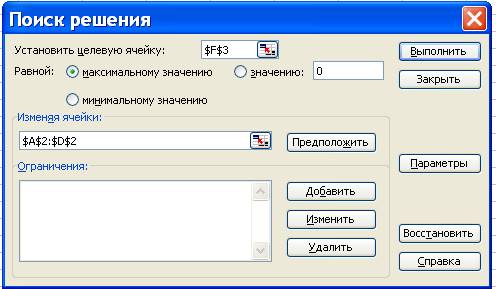
6. Назначить целевую функцию (установить целевую ячейку):
- курсор в строку Установить
целевую ячейку
- ввести адрес ячейки $F$3
-ввести направление целевой функции - Максимальному значению
-курсор в строку Изменяя
ячейки
-ввести адреса искомых переменных B$3:E$3
7. Ввести ограничения:
- указатель мышки на кнопку Добавить. Появляется диалоговое окно Добавление ограничения
- в строке Ссылка
на ячейку ввести адрес $Е$5
- ввести ограничения <=
- в строке Ограничение
ввести адрес $F$5
- указатель мыши на кнопку Добавить. На экране вновь диалоговое окно Добавление ограничения
- ввести остальные ограничения задачи, по
вышеописанному алгоритму
- после введения последнего ограничения кнопка ОК
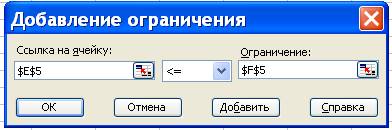
На экране появится диалоговое окно Поиск решения с введенными условиями.
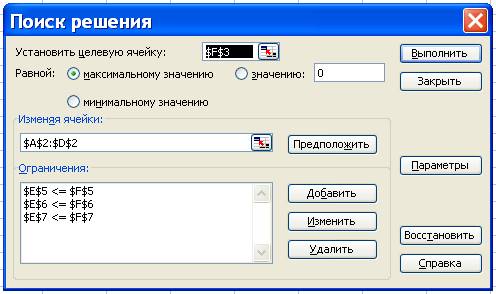
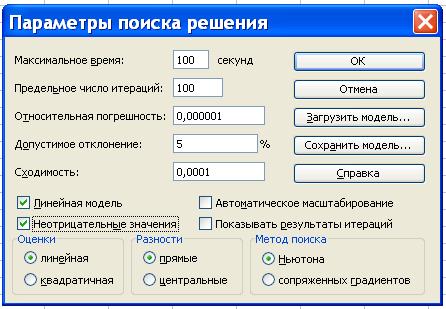
8.Ввести параметры для задачи:
- в диалоговом окне указатель мыши на кнопку Параметры. На экране появится
диалоговое окно Параметры поиска
решения.
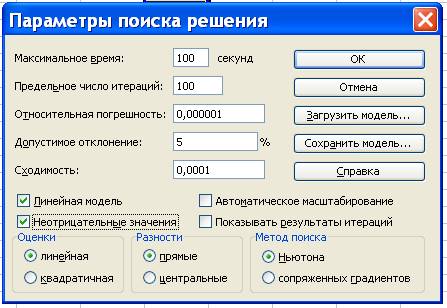
- установить флажки в окнах Линейная модель и Неотрицательные
значения
- указатель мыши на кнопку ОК. На экране диалоговое окно
Поиск решения.
- указатель мыши на кнопку Выполнить.
Далее появится диалоговое окно Результаты поиска решения и исходная таблица с заполненными
ячейками A2:D2 для
значений Хi и ячейка F3 с максимальным значением целевой функции:
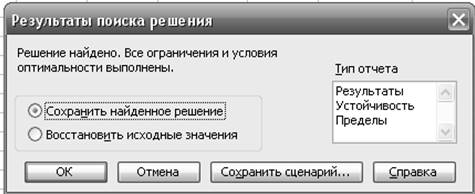
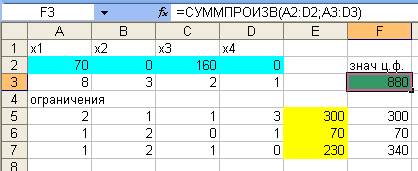
Полученное решение означает, что максимальный доход 880
ден. единиц при выпуске 300 ед.
продукции первого вида, 70 ед. продукции второго вида, и 230 ед. продукции 3
вида, при этом ресурсы первого и второго вида будут использованы полностью, а
из 340 ед. ресурса третьего вида будет
использовано 230 ед. (В данном случае под ресурсами понимается производительная
мощность токарного, фрезерного и шлифовального оборудования)
Excel позволяет представить результаты поиска решения в
форме отчета. Необходимо
проанализировать два отчета:
1.
Отчет результатов: В данный отчет включаются исходные и конечные значения целевой и
изменяемых ячеек, дополнительные сведения об ограничениях.
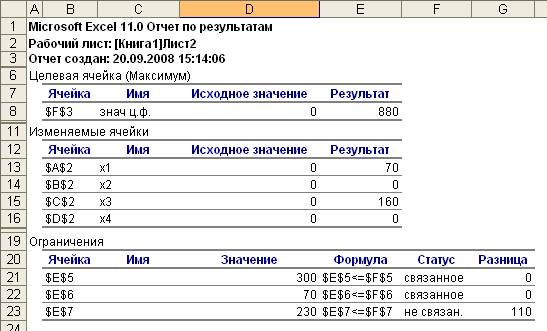
В отчете по результатам содержатся оптимальные
значения переменных Х1, Х2, Х3, Х4 равные соответственно 70, 0, 160, 0;
значение целевой функции –880, а также левые части ограничений: 300, 70, 230.
2.
Отчет
содержит сведения о чувствительности решения к изменениям в изменяемых ячейках
или в формулах ограничений:
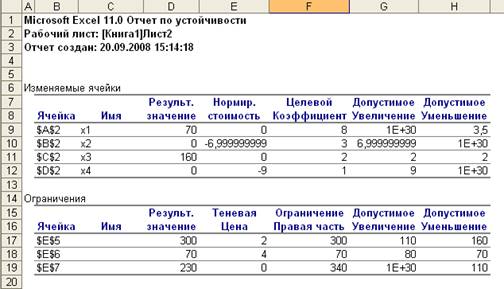
Он состоит из двух частей.
Первая часть содержит информацию, относящуюся к переменным:
·
результат решения
задачи (графа Результирующее значение);
·
нормируемая
стоимость, которая показывает, насколько изменится значение ЦФ в случае
принудительного включения единицы этой продукции в оптимальное решение;
·
коэффициенты
целевой функции (колонка Целевой коэффициент);
·
предельные
значения приращения целевых коэффициентов
Δсj, при которых сохраняется
первоначальное оптимальное решение (колонки
Допустимое увеличение, Допустимое уменьшение).
Во
второй части отчета содержится информация, относящаяся к
ограничениям:
·
величина использованных ресурсов (колонка
Результирующее
значение);
·
предельные значения приращения ресурсов Δbi. В колонке Допустимое уменьшение показано, насколько можно уменьшить (устранить излишек) или увеличить (повысить минимально необходимое требование) ресурс,
сохранив при этом структуру оптимального решения;
·
ценность дополнительной единицы ресурса i (колонка Теневая
цена). Рассчитывается только для дефицитных ресурсов.
Задача 2.
Нелинейная оптимизационная задача. Модель Марковца.
Имеется портфель ценных бумаг, состоящий из двух бумаг
А и В, при этом и бумага А и бумага В обладают собственной доходностью
(m) и собственным риском (σ). Так же дан коэффициент
корреляции R=0,18, который предполагает, что не такое количество
рыночных факторов влияет на бумагу А
активно влияют на бумагу В. Необходимо минимизировать риск, достигнув при
этом обязательной доходности.
Решение.
1. Сформулируем математическую модель задачи. Пусть x1
- удельный вес бумаг А в портфеле, x2 -
удельный вес бумаг В в портфеле.
Тогда m1 -
доходность бумаг А, m2 - доходность бумаг В, m3 -
доходность портфеля; σ1 -
риск бумаг А, σ2 - риск бумаг В, σ3 - риск портфеля в целом.
Для решения задачи используем EXCEL. Необходимо создать текстовую форму - таблицу для
ввода условий задачи и заполнить ее исходными данными.
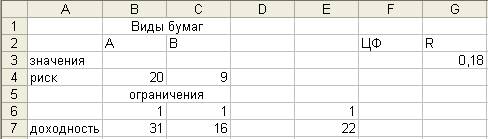
2. Ввести зависимость для целевой функции:
·
курсор в ячейку F3.
·
нажать на кнопку «Мастер функций», расположенную на
панели инструментов. На экране появляется диалоговое окно Мастер функций шаг 1 из 2:
·
в окне «Категория» нажать на категорию «Математические»;
·
в окне «Выберите функцию» нажать на КОРЕНЬ;
·
кнопка ОК. На экране появляется диалоговое
окно Аргументы функции КОРЕНЬ:
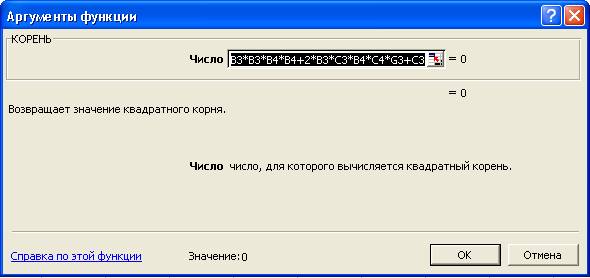
·
в строку «Число» необходимо ввести формулу B3*B3*B4*B4+2*B3*C3*B4*C4*G3+C3*C3*C4*C4;
·
нажать кнопку ОК. На экране: в ячейку F4 введена
функция:
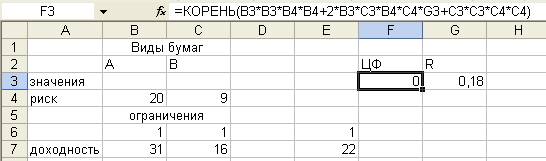
3. Ввести зависимости для ограничений:
·
курсор в ячейку D6.
·
Нажать на кнопку «Мастер функций», выбрать в категории «Математические» функцию СУММПРОИЗВ;
·
кнопка ОК.
·
в строку «Массив 1» ввести B3:C3;
·
в строку «Массив 2» ввести В6:C6;
·
кнопка ОК.
·
выполнить
аналогичные действия относительно ячейки D7.
·
в результате в
ячейки D6, D7 введены функции:
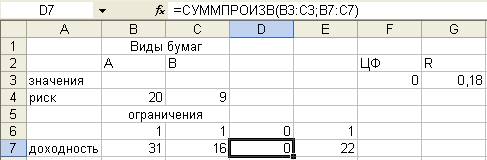
4.
В строке Меню нажать на вкладку Сервис. В развернутом меню выбрать Поиск решения. Появляется диалоговое
окно Поиск решения:
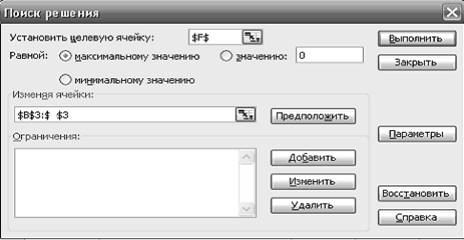
5. Назначить целевую функцию (установить целевую
ячейку):
·
курсор в строку Установить целевую ячейку;
·
ввести адрес
ячейки $F$3;
·
ввести
направление целевой функции – минимальному
значению;
·
курсор в строку Изменяя
ячейки;
·
ввести адреса
искомых переменных $B$3:$С$3.
6. Ввести ограничения:
·
нажать на кнопку Добавить. Появляется диалоговое окно Добавление ограничения:
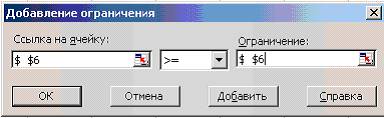
·
в строке Ссылка на ячейку ввести адрес $D$6;
·
ввести знак
ограничения >=;
·
в строке Ограничения ввести адрес $E$6;
·
нажать на кнопку Добавить.
·
ввести остальные
ограничения задачи по вышеописанному алгоритму;
·
после введения
последнего ограничения кнопка ОК.
На экране появится диалоговое окно Поиск решения с введенными условиями:
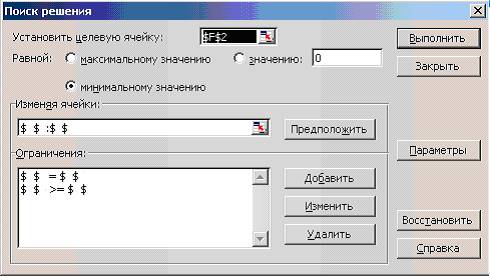
7. Ввести параметры для решения ЗЛП:
·
в диалоговом окне
нажать на кнопку Параметры. На
экране появляется диалоговое окно Параметры
поиска решения:
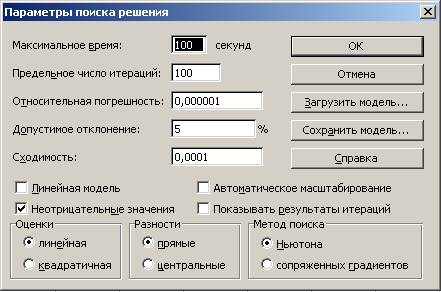
·
установить флажок
в окне Неотрицательные значения;
·
нажать на кнопку ОК. На экране диалоговое окно Поиск решения;
·
нажать на кнопку Выполнить.
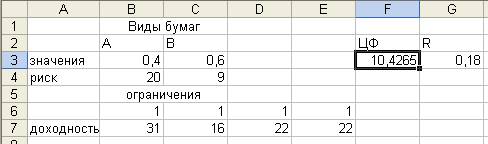
Далее появится диалоговое окно Результаты поиска решения и исходная таблица с заполненными
ячейками В3:D3 для
значений Хi и ячейка F4 с максимальным значением целевой функции:
Excel позволяет представить результаты поиска решения в
форме отчета.
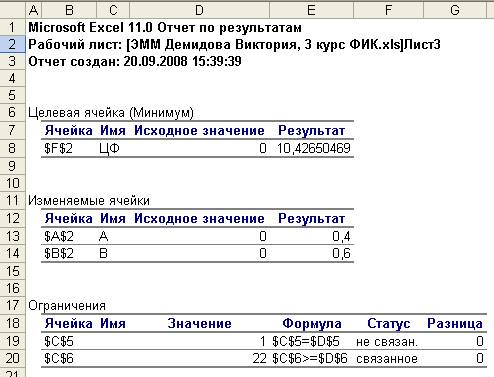
Отчет
результатов: в отчет включаются
исходные и конечные значения целевой и изменяемых ячеек, дополнительные
сведения об ограничениях.
Задача 3. Балансовые модели: Модель
Леонтьева
Даны
коэффициенты прямых затрат aij и конечный продукт Yi для трехотраслевой экономической системы:
А
= 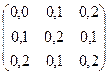 , Y =
, Y = 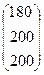
Требуется
определить:
1.
Коэффициенты
полных затрат.
2.
Вектор валового
выпуска.
3.
Межотраслевые
поставки продукции.
4.
Проверить
продуктивность матрицы А.
5.
Заполнить схему
межотраслевого баланса.
Решение.
Для
решения задачи воспользуемся функциями Excel.
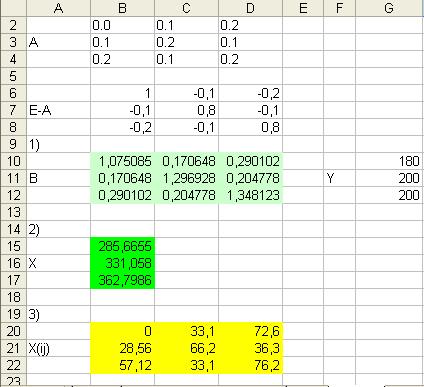
В
таблице приведены результаты решения задачи по первым трем пунктам.
1. В ячейки В6:D6 запишем
элементы матрицы E-A. Массив E-A задан как диапазон ячеек.
2. Вычислим матрицу коэффициентов полных затрат В = (E-A)-1. Выделим
диапазон В10:D12 для
размещения обратной матрицы и введем формулу для вычисления МОБР(В6:D8). Для того, чтобы ввести эту формулу, необходимо вызвать
«Мастера функций», щелкнув на значок на панели
инструментов, выбрать в окне Категории
выбрать «Математические». Далее в окне «Выберите функцию» выбрать МОБР и нажать кнопку ОК.
Появится
окно Аргументы функции в строку «Массив» введем ячейки B6:D8
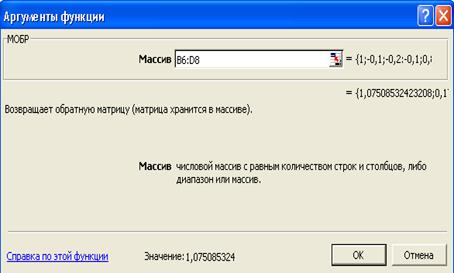
Затем
следует нажать клавиши CTRL + SHIFT + ENTER:
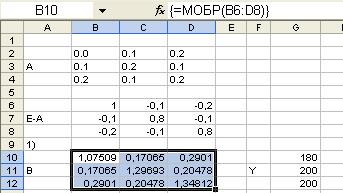
Все элементы матрицы коэффициентов полных затрат В
неотрицательны, следовательно, матрица А продуктивна (ответ на п. 1 и 4).
3. Вычислим вектор валового выпуска X по формуле X = BY.
В
ячейки G10:G12 запишем
элементы вектора конечного продукта Y. Выделим диапазон В15:D17 для
размещения вектора валового выпуска X. Затем
вводим формулу для вычислений МУМНОЖ
(В10:D12, G10:G12). Затем следует нажать клавиши CTRL + SHIFT + ENTER.
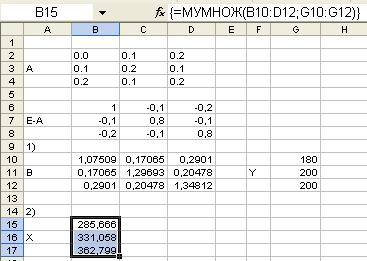
3. Межотраслевые поставки Xij вычисляю по формуле Xij = aijXj.
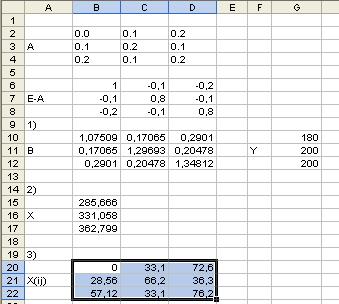
4. Далее заполняем схему межотраслевого баланса:
|
Производящие отрасли
|
Потребляющие отрасли
|
Конечный продукт
|
Валовый продукт
|
|
1
|
2
|
3
|
|
1
|
0
|
33,1
|
72,6
|
180
|
285,7
|
|
2
|
28,56
|
66,2
|
36,3
|
200
|
331,1
|
|
3
|
57,12
|
33,1
|
72,6
|
200
|
362,8
|
|
Условно чистая продукция
|
200,02
|
198,7
|
181,3
|
580
|
|
|
Валовой продукт
|
285,7
|
331,1
|
362,8
|
|
979,6
|
Задача 3. Транспортная задача
Исходные данные транспортной задачи приведены
схематически: внутри прямоугольника заданы удельные транспортные затраты на
перевозку единицы груза, слева указаны мощности поставщиков, а сверху –
мощности потребителей. Сформулировать экономико-математическую модель исходной
транспортной задачи, найти оптимальный план закрепления поставщиков за
потребителями, установить единственность или не единственность оптимального
плана, используя Поиск решения.
|
40
|
30
|
20
|
50
|
|
60
|
2
|
4
|
5
|
1
|
|
70
|
2
|
3
|
9
|
4
|
|
50
|
8
|
4
|
2
|
5
|
Решение.
Ввод условий задачи состоит из следующих основных
этапов:
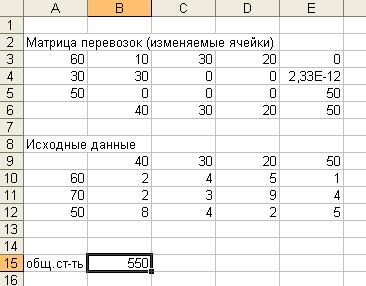
1. Создание формы для решения задачи предполагает создание
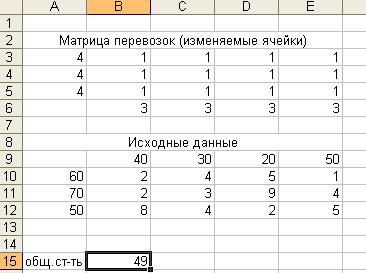
Матрицы перевозок. Для этого необходимо выполнить резервирование изменяемых ячеек: в блок ячеек В3:F6 вводится «1».
Так резервируется место, где после решения задачи
будет находиться распределение поставок, обеспечивающее минимальные затраты на
перевозку груза.
2. Ввод исходных данных:
В данном случае осуществляется ввод мощностей трех
мощностей поставщиков (ячейки А10:А12),
потребности регионов в их продукции (ячейки В9:Е9), а также удельные затраты по доставке от конкретного
поставщика потребителю (блок В10:Е12).
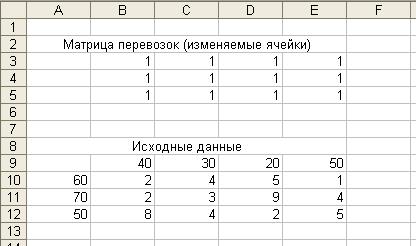
3. Ввод граничных условий.
а) Введение
условия реализации мощностей поставщиков:
Для этого необходимо выполнить следующие операции:
- курсор в ячейку А3;
- щелкнуть знак «∑»;
- выделить необходимые для суммирования ячейки В3:Е3;
- нажать ENTER – подтверждение ввода формулы для суммирования.
Аналогичные действия выполнить для ячеек А4, А5, т.е. ввести условия
реализации мощностей всех поставщиков (для всех строк).
б)Введение
условия удовлетворения запросов потребителей.
Для этого необходимо выполнить следующие операции:
- курсор в В6;
- щелкнуть знак «∑». При этом автоматически
выделяется весь столбец В3:В5;
- ENTER – подтверждение суммирования показателей выделенного
столбца.
Последовательность этих действий выполнить для ячеек С6-Е6.
Таким образом, введены ограничения для всех
поставщиков и всех потребителей.

4. Назначение целевой функции.
Для вычисления значения целевой функции,
соответствующей минимальным суммарным затратам на доставку груза, необходимо
зарезервировать ячейку и ввести формулу для ее вычисления.
Для этого:
- курсор в ячейку В15.
В данную ячейку будет помещаться значение целевой функции после решения задачи;
- щелкнуть Мастер
функций;
- в окне категория выбрать Математические;
- в окне Выберете
функцию выбрать СУММПРОИЗВ;
- ОК;
- в окне СУММПРОИЗВ
указать адреса массивов, элемент которых обрабатываются этой функцией.
В задаче целевая функция представляет собой
произведение удельных затрат на доставку груза (расположенных в блоке ячеек В10:Е12) и объемов поставок для каждого
потребителя (содержимое ячеек В3:Е5).
Для этого:
- в поле Массив
1 указать адреса В10:Е12;
- в поле Массив
2 указать адреса В3:Е5;
- нажать ОК
В поле ячейки В17
появится некоторое числовое значение, равное произведению единичных поставок на
удельные коэффициенты затрат по доставке грузов (число 49 в данной задаче):
5. Ввод зависимостей из математической модели.
Для осуществлении этого этапа необходимо выполнить
следующий перечень операций:
·
щелкнуть Сервис – Поиск решения;
·
курсор подвести в
поле Установить целевую ячейку;
·
вести адрес $B$15.
·
установить
направление изменения целевой функции, равное «минимальному значению»;
·
ввести адреса
изменяемых ячеек В3:Е5 . для этого:
- щелкнуть
в поле изменяя ячейки;
- ввести
адреса $B$3:$ Е$5.
Ввести ограничение задачи. В матрицу перевозок,
содержащую исходные данные по задаче, необходимо ввести условие реализации
мощностей всех поставщиков. Для этого:
- щелкнуть Добавить;
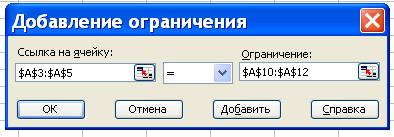
- в поле Ссылка
на ячейку ввести адреса $A$3:$А$5;
- в среднем поле установить знак « = »;
- в поле Ограничение
установить адреса $A$10:$A$12;
- щелкнуть ОК.
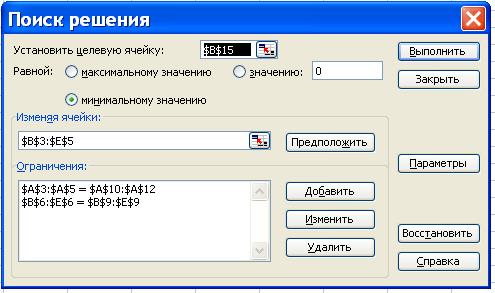
после этого мы вернемся в поле Поиск
решения.
Далее вводится ограничение, которое реализует условие
удовлетворения мощностей всех потребителей. Для этого:
- щелкнуть Добавить;
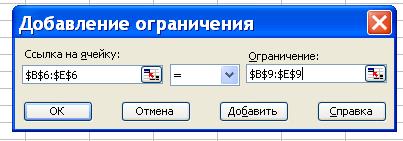
- в поле Ссылка
на ячейку ввести адреса $B$6:$Е$6;
- в среднем поле установить знак « = »;
- в поле Ограничение
установить адреса $B$9:$Е$9;
- нажать ОК
6. Ввод
параметров.
Далее необходимо установить ограничения на решение
задачи. Для этого:
- щелкнуть Параметры;
- установить Линейная
модель;
- установить Неотрицательные
значения, т.к. объемы поставок груза отрицательной величиной быть не могут.
- ОК. после
этого осуществится выход в поле Поиска
решений;
- нажать Выполнить.
Задача 5
В таблице заданы три временных ряда: первый из них
представляет нарастающую по кварталам прибыль коммерческого банка yt, второй и третий ряд- процентные ставки этого банка
по кредитованию юридических лиц x1t и
депозитным вкладам x2t за
этот же период.
|
16
|
20
|
22
|
14
|
25
|
28
|
25
|
28
|
30
|
31
|
|
30
|
34
|
40
|
38
|
22
|
48
|
50
|
52
|
53
|
49
|
|
25
|
27
|
30
|
31
|
35
|
27
|
42
|
41
|
43
|
42
|
Решение.
1. Внесем исходные данные:
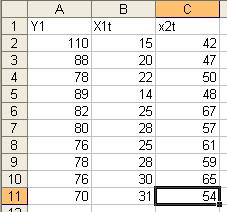
2. Для проведения регрессионного анализа выполним
следующие действия:
·
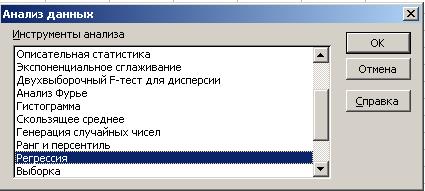
выберем команду Сервис => Анализ данных;
·
появилось
диалоговое окно Анализ данных, в этом
окне необходимо выбрать инструмент Регрессия,
а затем нажать кнопку ОК;
·
в диалоговом окне
Регрессия в поле «Входной интервал Y» введем
адрес одного диапазона ячеек, которой представляет зависимую переменную (А1:А11). В поле «Входной интервал X» введем адрес одного или нескольких диапазонов ячеек,
которые содержат значения независимых переменных (В1:С11);
·
Установить флажок
Метки в первой строке;
·
Выберем параметры
ввода. В данном примере установим переключатель «Новый рабочий лист»;
·
Поставить флажок
в поле Остатки;
·
Нажать кнопку ОК.
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
|
|
|
|
|
|
Множественный
R
|
0,819977
|
|
|
|
|
|
|
|
|
R-квадрат
|
0,672363
|
|
|
|
|
|
|
|
|
Нормированный
R-квадрат
|
0,578752
|
|
|
|
|
|
|
|
|
Стандартная
ошибка
|
7,227682
|
|
|
|
|
|
|
|
|
Наблюдения
|
10
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
|
|
|
Регрессия
|
2
|
750,4243
|
375,2121
|
7,182553
|
0,020131
|
|
|
|
|
Остаток
|
7
|
365,6757
|
52,23939
|
|
|
|
|
|
|
Итого
|
9
|
1116,1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
|
Y-пересечение
|
124,646
|
16,61091
|
7,503865
|
0,000137
|
85,36746
|
163,9246
|
85,36746
|
163,9246
|
|
X1t
|
-1,33503
|
0,596247
|
-2,23906
|
0,060161
|
-2,74493
|
0,074867
|
-2,74493
|
0,074867
|
|
x2t
|
-0,18495
|
0,432292
|
-0,42784
|
0,681625
|
-1,20716
|
0,837259
|
-1,20716
|
0,837259
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВЫВОД
ОСТАТКА
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное
Y1
|
Остатки
|
|
|
|
|
|
|
|
1
|
96,85263
|
13,14737
|
|
|
|
|
|
|
|
2
|
89,25272
|
-1,25272
|
|
|
|
|
|
|
|
3
|
86,02781
|
-8,02781
|
|
|
|
|
|
|
|
4
|
97,07796
|
-8,07796
|
|
|
|
|
|
|
|
5
|
78,87856
|
3,121441
|
|
|
|
|
|
|
|
6
|
76,72297
|
3,277034
|
|
|
|
|
|
|
|
7
|
79,98826
|
-3,98826
|
|
|
|
|
|
|
|
8
|
76,35307
|
1,646934
|
|
|
|
|
|
|
|
9
|
72,5733
|
3,426699
|
|
|
|
|
|
|
|
10
|
73,27272
|
-3,27272
|
|
|
|
|
|
|
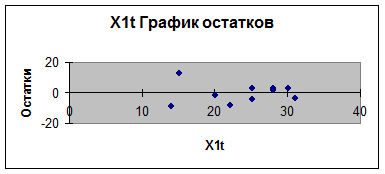
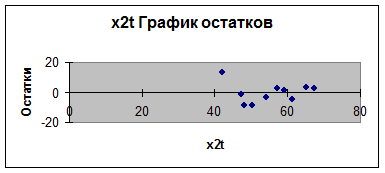
Уравнение регрессии зависимости прибыли от процентных
ставок по кредитованию юридических лиц и депозитным вкладам, полученное с
помощью EXCEL, имеет вид:
Y= 124,656+(-1,33503)x1+(-0,18495)x22+
e
Задача 6
Для
временного ряда Объем реализации
выбрать наилучший вид тренда и построить прогноз на два шага вперед. Данные за
16 месяцев приведены в таблице:
|
№
П/п
|
Реклама
|
|
1
|
4
|
|
2
|
4,8
|
|
3
|
3,8
|
|
4
|
8,7
|
|
5
|
8,2
|
|
6
|
9,7
|
|
7
|
14,7
|
|
8
|
18,7
|
|
9
|
19,8
|
|
10
|
10,6
|
|
11
|
8,6
|
|
12
|
6,5
|
|
13
|
12,6
|
|
14
|
6,5
|
|
15
|
5,8
|
|
16
|
5,7
|
Решение.
Для решения поставленной задачи необходимо выполнить
следующую последовательность действий:
·
выделить ячейки В1:В17, содержащие наименование
временного ряда и исходные данные;
·
Вызвать «Мастер диаграмм», щелкнув на
соответствующий значок на панели инструментов.
·
Выбрать тип
диаграммы: график; выбрать вид: первый (шаг 1);
·
Шаг 2. Щелкнуть
кнопку Далее;
·
Шаг 3. Щелкнуть
кнопку Далее;
·
Щелкнуть кнопку Готово. 
·
На экране -
построенный график.
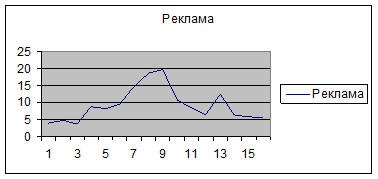
·
Щелкнуть правой
кнопкой мыши на линии полученного графика. График выделен метками. Выбрать Добавить линию тренда.
·
Выбрать тип Линейная в появившемся диалоговом окне Линия Тренда (потом Логарифмическая и Полиномиальная третьей степени).
·
Вкладка Параметры. Назначаем: показывать
уравнение на диаграмме.
·
Нажать ОК.