Задача 1.

Решите графическим методом задачу линейного программирования. Найти максимум и минимум функции при заданных ограничениях.

                            

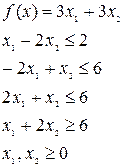
Решение:

Найдем оптимальное решение задачи , математическая модель которой имеет вид

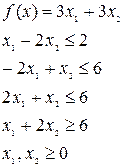
Построим прямые ограничений, для чего вычислим координаты точек пересечения этих прямых с осями координат (рис.2.2).

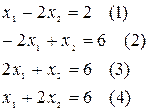
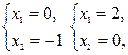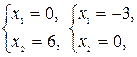(1) –    (2) –    (3) –

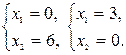
(4) –

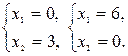
Рис.1. Графическое решение задачи 1

Определим ОДР. Например, подставим точку (0;0) в исходное ограничение (3), получим , что является истинным неравенством, поэтому стрелкой (или штрихованием) обозначим полуплоскость, содержащую точку (0;0), т.е. расположенную левее и ниже прямой (3). Аналогично определим допустимые полуплоскости для остальных ограничений и укажем их стрелками у соответствующих прямых ограничений (см. рис.1). Общей областью, разрешенной всеми ограничениями, т.е. ОДР является треугольник CFH.

Целевую прямую можно построить по уравнению

                                             

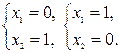
Строим вектор  из точки (0;0) в точку (1,1). Точка C– это последняя вершина области допустимых решений CFH, через которую проходит целевая прямая, двигаясь по направлению вектора . Поэтому C– это точка максимума ЦФ. Определим координаты точки C из системы уравнений прямых ограничений (3) и (2)

     ,

 

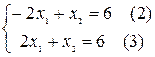
Максимальное значение ЦФ равно

Задача 2.

Решите симплекс-методом задачи линейного программирования.

                   

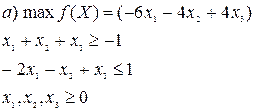
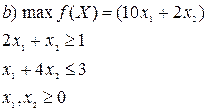
Решение:

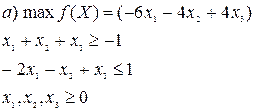
Приведем ЗЛП к каноническому виду:

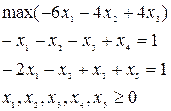
Все дальнейшие расчеты поместим в симплекс-таблицу :

Номер симплекс-таблицы	Базис	Cj Ci	В	-6	-4	4	0	0	Q
A1	A2	A3	A4	A5
0	A4	0	1	-1	-1	-1	1	0	-
A5	0	1	-2	-1	1	0	1	1
	-	0	6	4	-4	0	0	-
1	A4	0	2	-3	-2	1	0	1	-
A3	4	1	-2	-1	0	1	1	-
	-	4	10	0	0	0	4	-

В сисмплекс-таблице 1 получен оптимальный опорный план, т.к. все оценки . Оптимальные значения переменных . Максимальное значение функции равно 4.

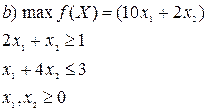
Приведем ЗЛП к каноническому виду:

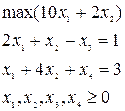
За базисные неизвестные примем , за свободные неизвестные - . Начальный опорный план имеет вид: (3,0,5,0).

Выразим базисные неизвестные через свободные:

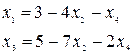
Тогда линейная форма:

 Все дальнейшие расчеты поместим в симплекс-таблицу :

Номер симплекс-таблицы	Базис	Cj Ci	В	0	-38	0	-40	Q
A1	A2	A3	A4
0	A1	0	3	1	4	0	1	¾
A3	0	5	0	7	1	2	5/7
	-	30	0	38	40	0	-

В сисмплекс-таблице 0 получен оптимальный опорный план, т.к. все оценки . Оптимальные значения переменных . Максимальное значение функции равно 30.

Задача 3.

Используйте аппарат теории двойственности для экономико-математического анализа оптимального плана ЗЛП.

Предприятие выпускает четыре вида продукции и использует три вида оборудования: токарное, фрезерное, шлифовальное. Общий фонд рабочего времени оборудования каждого вида, нормы расхода и цены реализации единицы каждого вида продукции приведены в таблице:

Тип оборудования	Нормы расхода сырья на одно изделие	Фонд рабочего времени
А	Б	В	Г
Токарное	2	1	1	3	300
Фрезерное	1	0	2	1	70
Шлифовальное	1	2	1	0	340
Цена изделия	8	3	2	1

 При решении задачи на максимум общей стоимости выпускаемой продукции ( вся готовая продукция реализуется) были получены следующие результаты:

Требуется:

1) сформулировать прямую оптимизационную задачу на максимум общей  стоимости выпускаемой продукции, пояснить нулевые значения ;

2) сформулировать двойственную задачу и найти ее оптимальный план;

3) проанализировать использование ресурсов в оптимальном плане;

4) определить, как изменяется общая стоимость продукции и план ее выпуска, если фонд рабочего времени шлифовального оборудования увеличить на 24 часа;

5) определить целесообразность включения в план изделия «Д» ценой 11 ед., если нормы затрат оборудования 8,2 и 2 ед. соответственно.

Решение:

1) Обозначим через =1,4 – объем выпуска деталей j- го вида и запишем математическую модель задачи критерию «максимум цены изделия»:

                                        

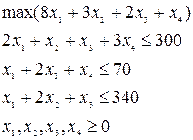
Проверим, как удовлетворяется система функциональных ограничений оптимальным планом :

                       (*)

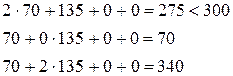Значение целевой функции при этом плане равно:

Нулевые значения означают, что токарный станок используется полностью.

2) Двойственная задача имеет вид:

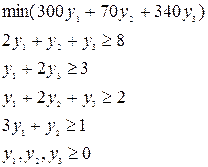
Для нахождения оценок используем вторую теорему двойственности. Поскольку первое ограничение в (*) выполняется как строгое неравенство, то  . Так как и , то получаем следующую систему для получения двойственных оценок:

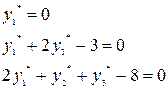
Решая ее получим: .

Вычислим значение целевой функции двойственной задачи:

т.е .

3) В рассматриваемом примере увеличение нормы расхода сырья на одно изделие при работе на токарном станке не повлияет на оптимальный план выпуска продукции, а на шлифовальном станке привело бы к росту максимальной цены на 13/2 у.е. и на фрезерном- на 3/2 у.е.. Не дефицитным ресурсом является расход сырья на токарном станке, острее ощущается дефицитность ресурса шлифовального станка.

4) Определим как изменится общая стоимость продукции и план ее выпуска, если фонд рабочего времени шлифовального оборудования увеличить на 24 часа.

Тогда имеем:

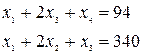
т.е.

Отсюда определяется план цен в новых производственных условиях- соответственно общая стоимость изделий составит 980 у.е.,т.е. возрастет на 15 у.е.

5) определим целесообразность включения в план изделия «Д» ценой 11 ед., если нормы затрат оборудования 8,2 и 2 ед. соответственно. Имеем:

- невыгодно.

Задача 4.

Заданы матрица коэффициентов прямых затрат трех отраслей и вектор конечной продукции . Требуется:

1)    проверить продуктивность матрицы ;

2)    построить баланс производства и распределения продукции отраслей

отрасли	Коэффициенты прямых затрат	Конечный продукт
1	2	3
1	0,1	0,2	0,4	100
2	0,0	0,4	0,1	200
3	0,1	0,3	0,4	100

 

Решение:

1) Проверим продуктивность матрицы

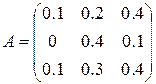
Оценку произведем по первому признаку продуктивности.

Рассмотрим матрицу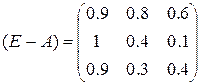

Найдем для нее обратную матрицу

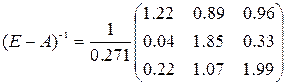
так  все элементы обратной матрицы положительны, то матрица  продуктивна.

2) Модель баланса производства и распределения продукции предприятия можно представить следующей системой уравнений:

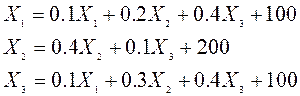
Решение найдем с помощью обратной матрицы.

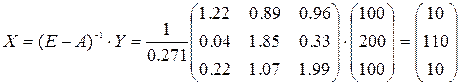
Распределение продукции между цехами на внутреннее потребление определяем из соотношения

 т.е.

, , ,

, , ,

, ,

В итоге плановая модель – баланс производства и распределения продукции предприятия – будет иметь следующий вид:

Межпродуктовый баланс производства и распределения продукции
Производящие структуры	Потребляющие структуры	Конечный продукт	Валовый продукт
1	2	3
1	1	22	4	100	10
2	0	11	10	200	110
3	1	33	4	100	10
Итого	2	66	18	400	230

Задача 5.

Требуется:

1)    сгладить с помощью простой скользящей средней;

2)    определить наличие тренда ;

3)    построить линейную модель , параметры которой оценить МНК;

4)    построить адаптивную модель Брауна  с параметром сглаживания ; выбрать лучшее значение ;

5)    оценить адекватность построенных моделей на основе исследования:

·        случайности остаточной компоненты по критерию пиков;

·        независимости уровней ряда остатков по d-критерию ( в качестве остатков используйте уровни d₁=1.08 и d₂=1.36) или по первому коэффициенту корреляции, критический уровень которого r(1)=0,36;

·        нормальности распределения остаточной компоненты по R/S- критерию с критическими уровнями 2.7-3.7;

·        для оценки точности модели используйте среднее квадратическое отклонение и среднюю по модулю ошибку;

6)    Построить точечный и интервальный прогнозы на два шага вперед (для вероятности P=70% используйте коэффициент K_p=1.05) по двум построенным моделям.

Вычисления провести с одним знаком в дробной части. Основные промежуточные результаты вычислений представить в таблицах.

Решение:

Проведем расчеты и заполним таблицу 5.1.

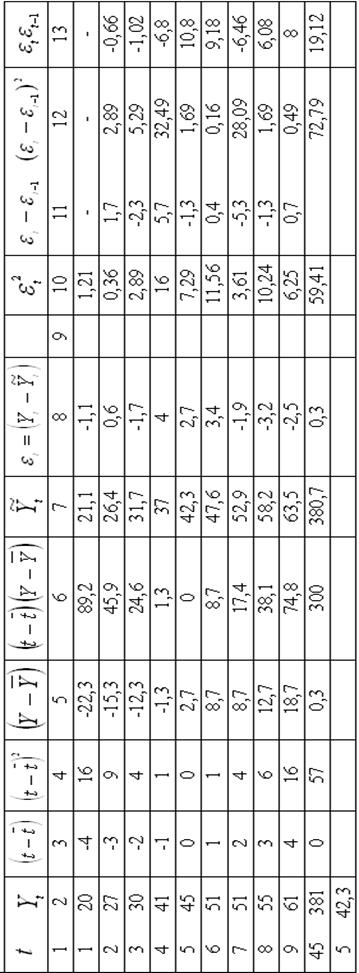
По данным этой таблицы построим график:

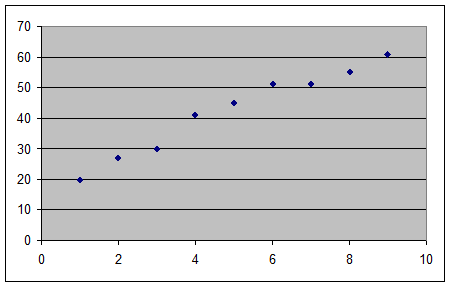
Оценка параметров уравнений регрессии осуществляется методом наименьших квадратов. Сущность метода наименьших квадратов заключается в нахождении параметров модели a и b, при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических. Для выражения прямолинейной формы зависимости между X и Y применяется формула:

Для расчета параметров a и b линейной регрессии решаем систему уравнений:

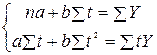
Для определения параметров уравнения на основе требований метода наименьших квадратов составляется система нормальных уравнений:

      

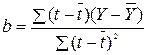
Найдем коэффициенты a и b:

Таким образом, уравнение линии регрессии имеет вид:

Для проверки адекватности модели проведем следующие расчеты

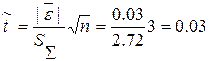
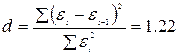
При проверки независимости уровней ряда остатков друг от друга значение d=1.2, при уровне значимости a= 0,3 попадает в интервал между d₁=1.08 и d₂=1.36, т.е. в область не определенности. Поэтому воспользуемся следующей формулой

Сопоставляя это число с табличным значением первого коэффициента автокорреляции 0,36 , увидим, что расчетное значение меньше табличного. Это означает, что с ошибкой в 1% ряд остатков можно считать некоррелированными.

Соответствие ряда остатков нормальному закону проверим с помощью формулы. Тогда критерий .