Доработка
1. Стадии инвестиционного процесса
В самом общем виде инвестиционный процесс распадается на три стадии (фазы): предынвестиционную, собственно инвестицилнную и эксплуатационную.[1] Указанные фазы инвестиционного процесса, в свою очередь, распадаются на ряд этапов, как показано на рисунке ниже.
 |
2. Методика расчета показателей эффективности инвестиционного проекта
В основе процесса принятия управленческих решений инвестиционного характера лежат оценка и сравнение объема предполагаемых инвестиций и будущих денежных поступлений. Методы, используемые в анализе инвестиционной деятельности, можно подразделить на две группы:
а) основанные на дисконтированных оценках;
б) основанные на учетных оценках.
Рассмотрим ключевые идеи, лежащие в основе этих методов.
1) Метод расчета чистого приведенного эффекта
Этот метод основан на сопоставлении величины исходной инвестиции (IС) с общей суммой дисконтированных чистых денежных поступлений, генерируемых ею в течение прогнозируемого срока. Поскольку приток денежных средств распределен во времени, он дисконтируется с помощью коэффициента r, устанавливаемого аналитиком (инвестором) самостоятельно, исходя из ежегодного процента возврата, который он хочет, или может, иметь на инвестируемый им капитал.
Допустим, делается прогноз, что инвестиция (IС) будет генерировать в течение n лет, годовые доходы в размере Р1, Р2, Р3. Общая накопленная величина дисконтированных доходов (РV) и чистый приведенный эффект (NРV) соответственно рассчитывается по формуле:
![]()
![]()
Очевидно, что если: NРV > 0, то проект следует принять;
NРV < 0, то проект следует отвергнуть;
NРV = 0, то проект ни прибыльный, ни убыточный.
При прогнозировании доходов по годам необходимо по возможности учитывать все виды поступлений как производственного, так и непроизводственного характера, которые могут быть ассоциированы с данным проектом. Так, если по окончании периода реализации проекта планируется поступление средств, в виде ликвидационной стоимости оборудования или высвобождения части оборотных средств, они должны быть учтены как доходы соответствующих периодов.
Необходимо отметить, что показатель NРV отражает прогнозную оценку изменения экономического потенциала предприятия в случае принятия рассматриваемого проекта. Этот показатель аддитивен во временном аспекте, т. е. NРV различных проектов можно суммировать. Это очень важное свойство, выделяющее этот критерий из всех остальных и позволяющее использовать его в качестве основного при анализе оптимальности инвестиционного портфеля.
2) Метод расчета индекса рентабельности инвестиции
Этот метод является, по сути, следствием предыдущего - индекс рентабельности (РI) рассчитывается по формуле:
![]()
Очевидно, что если: РI >1, то проект следует принять;
РI <1, то проект следует отвергнуть;
РI = 1, то проект ни прибыльный, ни убыточный.
В отличие от чистого приведенного эффекта индекс рентабельности является относительным показателем. Благодаря этому он очень удобен при выборе одного проекта из ряда альтернативных, имеющих примерно одинаковые значения NРV, либо при комплектовании портфеля инвестиций с максимальным суммарным значением NРV.
3) Метод расчета нормы рентабельности инвестиции
Под нормой рентабельности инвестиции (IRR) понимают значение коэффициента дисконтирования, при котором NPV проекта равен нулю:
![]()
Смысл расчета этого коэффициента при анализе эффективности планируемых инвестиций заключается в следующем: IRR показывает максимально допустимый относительный уровень расходов, которые могут быть ассоциированы с данным проектом. Например, если проект полностью финансируется за счет ссуды коммерческого банка, то значение IRR показывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которого делает проект убыточным.
На практике любое предприятие финансирует свою деятельность, в том числе и инвестиционную, из различных источников. В качестве платы за пользование авансированными в деятельность предприятия финансовыми ресурсами оно уплачивает проценты, дивиденды, вознаграждения и т. п., т. е. несет некоторые обоснованные расходы на поддержание своего экономического потенциала. Показатель, характеризующий относительный уровень этих расходов, можно назвать «ценой» авансированного капитала (СС). Этот показатель отражает сложившийся на предприятии минимум возврата на вложенный в его деятельность капитал, его рентабельность и рассчитывается по формуле средней арифметической взвешенной.
Экономический смысл этого показателя заключается в следующем: предприятие может принимать любые решения инвестиционного характера, уровень рентабельности которых не ниже текущего значения показателя СС (или цены источника средств для данного проекта, если он имеет целевой источник). Именно с ним сравнивается показатель IRR, рассчитанный для конкретного проекта, при этом связь между ними такова.
Если: IRR > СС, то проект следует принять;
IRR < СС, то проект следует отвергнуть;
IRR = СС, то проект ни прибыльный, ни убыточный.
Практическое применение данного метода осложнено, если в распоряжении аналитика нет специализированного финансового калькулятора. В этом случае применяется метод последовательных итераций с использованием табулированных значений дисконтирующих множителей. Для этого с помощью таблиц выбираются два значения коэффициента дисконтирования r1<r2 , таким образом, чтобы в интервале (r1;r2) функция NPV=f(r) меняла свое значение с «+» на «–» или с «–» на «+». Далее применяют формулу:
![]()
где r1 – значение табулированного коэффициента дисконтирования, при котором f(r1)>0 (f(r1)<0);
r2 – значение табулированного коэффициента дисконтирования, при котором f(r2)<0 (f(r2)>0).
3. Решение уравнения
![]()
Решим это уравнение графическим способом с применением пакета Excel. Для этого рассмотрим функцию
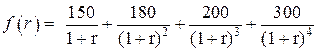 ,
,
построим ее график и для поиска корня уравнения посмотрим, при каком значении аргумента значение функции равно 500.
Для этого в строку формул введем выражение:
=150/(1+A2)+180/((1+A2)*(1+A2))+200/((1+A2)*(1+A2)*(1+A2))+ +300/((1+A2)*(1+A2)*(1+A2)*(1+A2)),
где А2 означает адрес ячейки со значением аргумента.
Далее с помощью автозаполнения получим столбик значений аргумента от 0 до 1 с шагом 0,05; также с помощью автозаполнения получим столбик значений функции по приведенной выше формуле, затем построим график этой функции.
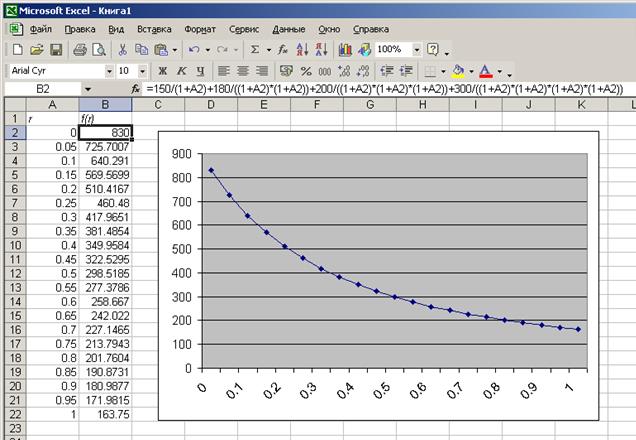
Из графика видно, что значение функции равное 500 приблизительно соответствует значению аргумента, равному 0,21.
Вычислим:
![]() ;
;
![]() ;
;
![]() .
.
Значит, с хорошей точностью можно полагать, что r=0,21, т.е. r=21%.
[1] Справочник финансиста предприятия / Группа авторов. – М.: ИНФРА-М, 2003. – с. 259.