Содержание
Теоретическая
часть: Прогнозирование вероятности банкротства. 3
1. Сущность и модели финансового прогнозирования. 3
1.1.
Методы экстраполяции. 3
1.2.
Методы математического моделирования. 6
2. Методы прогнозирования
вероятного банкротства. 8
2.1.
Метод анализа прогнозирования
банкротства на основе
стационарного ряда 8
2.2.
Элементы экстраполярного прогнозирования и интерполяции. 12
2.3.
Особенности метода прогнозирования банкротства
на основе тренда и колеблемости. 15
2.4.
Прогнозирование банкротства на основе
модели Альтмана. 18
2.5. Метод экспертных оценок. 26
2.6.
Метод построения прогнозной отчетности. 28
Практическая часть. 31
Список
литературы.. 42
Теоретическая часть: Прогнозирование вероятности
банкротства
1. Сущность и модели финансового прогнозирования
1.1. Методы экстраполяции
Формализованные методы прогнозирования банкротства базируются на
математической теории, которая
обеспечивает повышение достоверности и точности прогнозов, значительно
сокращает соки их выполнения, позволяет облегчить деятельность по обработке
информации и оценке результатов. В составе
формализованных методов анализа качества прогнозирования входят: методы экстраполяции
и методы математического моделирования.
В данной главе рассмотрим основные из методов прогнозирования банкротства, используемые
в экономической науке[1,2 и др.].
Термин «экстраполяция» имеет несколько толкований. В широком смысле слова
экстраполяция- это метод научного исследования, заключающийся в распространении
выводов, полученных из наблюдения над одной частью явления, на другую его
часть. В узком смысле слова экстраполяция означает нахождение по ряду данных
функций других ее значений, находящихся вне этого ряда. Экстраполяция
заключается в изучении сложившихся в прош8лом и настоящем устойчивых тенденций
экономического развития и перенесении их на будущее. В прогнозировании
экстраполяция применяется при изучении временных рядов экономических
показателей и представляет собой нахождение
значений функций за пределами области ее определения с использованием информации
о поведении данной функции в некоторых точках, принадлежащих области ее определения.
Различают перспективную и ретроспективную экстраполяцию. Перспективная
означает продолжение уровней ряда динамики на будущее на основе выявленной
закономерности изменения уровней в изучаемом отрезке времени. Ретроспективная
экстраполяция характеризуется продолжением уровней динамики в прошлое.
Понятием, противоположным экстраполяции является интерполяция,
интерполирование, которое предусматривает нахождение промежуточных значений
функции в области ее определения. При изучении временных рядов в случае
необходимости может производиться интерполирование промежуточных уровней.
Разграничивают формальную и прогнозную экстраполяцию. Формальная
экстраполяция базируется на предположении и сохранении в будущем прошлых и
настоящих тенденций развития объекта. Прогнозная экстраполяция увязывает
фактическое состояние исследуемого объекта с гипотезами о динамики его
развития. Она предполагает необходимость учета в перспективе альтернативных
изменений самого объекта, его сущности.
При формировании прогнозов
банкротства с помощью экстраполяции исходят из статистически
складывающихся тенденций изменения тех или иных количественных характеристик
банкротства. Экстраполируются оценочные функциональные системные и структурные
характеристики, например, количественные характеристики экономического,
научного, производственного потенциала при оценке банкротства. Степень
реальности такого рода прогнозов в значительной степени обуславливается
аргументированностью выбора пределов экстраполяции и стабильностью соответствия
«измерителей по отношению к сущности рассматриваемого явления.
Последовательность действий при статистическом анализе тенденций и
экстраполировании состоит в следующем[3, с. 28]:
1)
четкое определение задачи, выдвижение гипотез о
возможном развитии прогнозируемого объекта, обсуждение факторов, стимулирующих
развитие данного объекта, определение необходимой экстраполяции и ее допустимой
дальности;
2)
выбор системы параметров;
3)
сбор и систематизация данных;
4)
выявление тенденций или симптомов изменения изучаемых
величин в ходе статистического анализа данных.
Для повышения точности экстраполяции используются различные приемы.
Например, экстраполируемая часть общей
кривой развития (тренд) корректируется с учетом реального опыта
функционирования отрасли- аналога исследований объекта, опережающих в своем
развитии прогнозируемый объект.
Тренд- это изменение, определяющее общее направление развития организации
в отношении банкротства, основную тенденцию временных рядов. Под ним понимается
характеристика основной закономерности движения во времени, в некоторой мере
свободной от случайных воздействий. Тренд- это длительная тенденция изменения
экономических показателей. При разработке моделей прогнозирования банкротства тренд оказывается основной
составляющей прогнозируемого временного ряда экономических показателей, на которую
уже накладываются другие составляющие.
Сущность метода наименьших квадратов состоит в отыскании параметров
модели тренда, минимизирующих ее отклонение от
точек исходного временного ряда, то есть минимизации суммы
квадратических отклонений между наблюдаемыми и расчетными величинами. Модель
тренда может различаться по виду. Ее выбор в каждом конкретном случае
осуществляется в соответствии с рядом статистических критериев. Наибольшее
распространение в практических исследованиях получили следующие функции:
линейная, квадратичная, степенная, показательная, экспоненциальная,
логистическая. Особенно широко применяется линейная функция, то есть сводимая к
линейной форме, как наиболее простой и в достаточной степени удовлетворяющей
исходным данным. Метод наименьших квадратов широко применяется при анализе методов качества прогнозов в силу своей
простоты и возможности реализации на компьютере. Недостаток данного метода
состоит том, что модель тренда жестко
фиксируется, а это делает возможным его применение только при небольших периодах
упреждения, то есть при краткосрочном прогнозировании[5, с. 145].
Метод экспоненциального сглаживания дает возможность получить оценки
параметров тренда банкротства , характеризующих
не средний уровень процесса, а тенденцию, сложившуюся к моменту
последнего наблюдения. Этот метод позволяет оценить параметры модели,
описывающей тенденцию, которая сформировалась в конце базисного периода. Он не
просто экстраполирует действующие зависимости в будущее, а приспосабливается,
адаптируется к изменяющимся условиям во
времени.
Этот метод применяется при анализе прогнозов банкротства при кратко- и среднесрочном
прогнозировании. Его преимущества состоят в том, что он не требует обширной
информационной базы и предполагает ее интенсивный анализ с точки зрения
информационной ценности различных членов временной последовательности. Модели,
описывающие динамику показателя, имеют простую математическую формулировку,
адаптивная эволюция параметров позволяет отразить неоднородность свойств временного ряда.
Метод скользящей средней дает возможность выравнивать динамический ряд
путем его расчленения на равные части с обязательным совпадением в каждой из
них сумм модельных и эмпирических значений.
В целом, методы экстраполяции, основанные на продлении тенденций прошлого
и настоящего на будущий период, могут использоваться при анализе
прогнозов банкротства лишь при
периоде упреждения до пяти или семи лет. Важнейшим условием использования
данных моделей является наличие устойчивых
выраженных тенденций развития банкротства.
При более длительных прогнозах эти методы не дают точных результатов.
1.2. Методы математического
моделирования
Распространенной методикой при анализе
прогнозов банкротства служит
моделирование, которое следует понимать как исследование объектов познания на
их моделях. Оно предполагает построение моделей реально существующих предметов
и явлений: живых организмов, инженерных конструкций, общественных систем.
Моделирование считается достаточно эффективным средством прогнозирования и при
оценке вероятности банкротства.
В научной литературе термин
«модель» означает какой-либо условный образ объекта исследования. Модель- это
схема, изображение или описание какого- либо явления или процесса в природе или
обществе. Модель констатируется субъектом исследования так, чтобы операции
отображали характеристики объекта, существенные для цели исследования. Модель -
один из важнейших инструментов социально- экономического прогнозирования, научного
познания исследуемого объекта. Поэтому вопрос об адекватности модели объекту
правомерно решать лишь относительно определенной цели.
Содержанием процесса моделирования являются: конструирование модели на
основе предварительного изучения объекта или процесса, выделение его
существенных характеристик или признаков, теоретический или экспериментальный
анализ модели, сопоставление результатов моделирования с фактическими данными об объекте,
корректировка или уточнение модели[7, с. 45].
Для описания моделей используется математический аппарат. Это связано с
преимуществами математического подхода к многостадийным процессам обработки
информации, использованием идентичных средств формирования задач, поиска
методов решения, фиксации этих методов и их преобразования в программы,
рассчитанные на применение средств вычислительной техники.
Средством изучения закономерностей развития социально- экономических
явлений является экономико-математическая модель. Под экономико-математической
моделью (ЭММ) понимается методика доведения до полного, исчерпывающего описание
процесса получения и обработки исходной информации и правил решения
рассматриваемой задачи в достаточно широком спектре конкретных случаев. ЭММ -
это система формализованных соотношений, описывающих основные взаимосвязи
элементов, образующих экономическую систему.
Эконометрия- наука, изучающая конкретные количественные взаимосвязи
экономических процессов с помощью экономико-математических методов и моделей.
Эконометрическое моделирование основано на обработке статистической информации
ретроспективного характера о банкротстве
, оценке отдельных переменных величин, их параметров. Простейшая ЭММ может быть
представлена в следующем виде [9, с.30]:
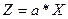 , (1)
, (1)
где Z – общая потребность в материалах
а – норма расхода материала на одно
изделие,
х – количество изделий
Эта модель может быть использована и
при анализе прогнозов банкротства.
ЭММ приобретает более сложный вид, если
определяется потребность в материалах для изготовления нескольких видов
изделий:
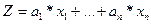 , (2)
, (2)
где n= 1,2, 3 …,n
Эта модель показывает зависимость
потребности материалов от двух факторов: количества изделий и норм расхода
материалов. Она называется дескриптивной (описательной).
Применение математических методов
является необходимым условием для разработки и использования методов
моделирования в прогнозировании банкротства, что обеспечивает большую степень
согласованности действенности и своевременности прогнозов. Особенно широко
методы математического моделирования используются при анализе прогнозов
банкротства
2. Методы прогнозирования вероятного банкротства
2.1. Метод анализа
прогнозирования банкротства на основе стационарного ряда
Временный ряд называется стационарным, если в нем отсутствует тенденция
развития.[5, с. 127].
Это означает, что уровни динамического ряда варьируют вокруг среднего
уровня, отклонения от которого представляют собой случайную колеблемость.
Модель для динамического ряда имеет
следующий вид:
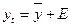 , (3)
, (3)
где yt- уровни динамического ряда,
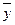 - средний за
период уровень динамического ряда,
- средний за
период уровень динамического ряда,
Е –
случайная составляющая, определяемая по формуле (4):
Е = уt - 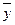 , (4)
, (4)
Графически
стационарный ряд можно представить на рисунке 1
 у
у
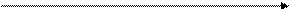 время
время
Рис. 1. Графическая модель
стационарного ряда
Такие ряды в экономике сравнительно редки. Чаще
встречаются ряды с тенденцией. Вместе с
тем они могут иметь место при изучении динамики рядов из относительных средних величин. Например, спрос на товар при
отсутствии резких изменений цен на него и одинаковом сегменте рынка.
Если стационарный ряд разбить на две равные по
времени части, то средние уровни по этим частям не должны существенно
различаться, то есть 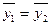 . Если в двух сравниваемых частях динамического ряда
дисперсии уровней различаются несущественно, то проверка равенства средних
уровней осуществляется по t-
критерию Стьюдента по формуле:
. Если в двух сравниваемых частях динамического ряда
дисперсии уровней различаются несущественно, то проверка равенства средних
уровней осуществляется по t-
критерию Стьюдента по формуле:
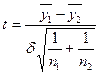 , (5)
, (5)
где n1=n2-
число уровней в каждой половине динамического ряда;
δ – среднее квадратическое
отклонение разности средних величин, определяемое по формуле (6)
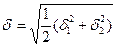 , (6)
, (6)
где δ12 , δ22
– групповые дисперсии, определяемые по формулам (7) и(8).
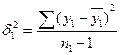 , (7)
, (7)
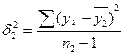 , (8)
, (8)
Непосредственному применению формулы
(5) для оценки существенности различий сравниваемых средних уровней
предшествует статистическая проверка по F – критерию Фишера по
формуле (9):
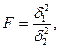 (9)
(9)
где 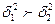
Рассмотрим изложенные выше выводы на
конкретно примере. Пусть прибыль предприятия за год характеризуется данными,
приведенными в таблице 1[8, с. 38]
Таблица 1
Исходные данные
|
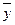 ,тыс. руб. ,тыс. руб.
|
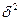
|
|
1 полугодие
|
63,5
|
0,92
|
|
2 полугодие
|
64,5
|
0,86
|
Проведем прогноз вероятного банкротства при использовании
стационарного (временного ряда).
Оценим существенность различий в
дисперсиях: F =
0,92/0,86 = 1,07 при табличном значении 5,05. Дисперсии можно признать равными.
Тогда оценим существенность расхождения
в среднемесячных уровнях прибыли за каждое полугодие по t – критерию Стьюдента:
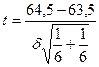
где
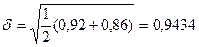 .
.
Произведя дальнейшие вычисления,
находим, что t= 1,84.
Это меньше t табличного=
2,23. Следовательно, с вероятностью 0,95 можно признать, что тенденции
появления банкротства в ряду динамики
нет.
Прогноз по стационарному ряду основан
на предположении о неизменности в будущем среднего уровня динамического ряда,
то есть ур= 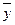 , где ур - прогнозное значение. Так как средний
уровень динамического ряда имеет погрешность как выборочная средняя, кроме
того, отдельные уровни ряда колеблются вокруг среднего значения, принято
прогноз давать в интервале:
, где ур - прогнозное значение. Так как средний
уровень динамического ряда имеет погрешность как выборочная средняя, кроме
того, отдельные уровни ряда колеблются вокруг среднего значения, принято
прогноз давать в интервале:
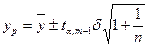 , (10)
, (10)
где 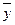 - среднее значение по динамическому ряду
- среднее значение по динамическому ряду
δ – среднее квадратическое
отклонение по динамическому ряду
n – длина динамического ряда
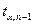 - табличное значение
критерия Стьюдента при уровне значимости и числе степенней свободы (n-1).
- табличное значение
критерия Стьюдента при уровне значимости и числе степенней свободы (n-1).
Для нашего примера:
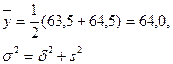
где δ2- межгрупповая дисперсия,
s2 – внутригрупповая дисперсия
δ2
= 0,25
s2= (0,92+0,86)/2
= 089
Тогда,
σ2= 0,25 + 0,89 = 1,14
σ=
1,0677
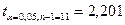
Тогда
ошибка прогноза банкротства составит :
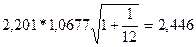 .
.
Соответственно прогноз прибыли на
январь следующего года окажется таким:
61,6≤
ур ≤ 66,4
Это означает, что в следующем году
предприятие получит прибыль и банкротом не станет.
Данный
метод может быть использован для краткосрочного прогноза.
2.2. Элементы
экстраполярного прогнозирования и интерполяции
Применение экстраполяции при прогнозировании вероятного банкротства базируется на следующих основных принципах[8,
с. 392]:
-
развитие исследуемого явления в целом следует описывать
плавной кривой;
-
общая тенденция развития явления в прошлом и настоящем
не должна претерпевать серьезных изменений в будущем.
Поэтому надежность и точность прогноза банкротства зависят от того, насколько близкими к
действительности окажутся эти предположения. Экстраполяцию следует
рассматривать как начальную стадию построения окончательных прогнозов
банкротства. Всегда следует учитывать все необходимые условия, предпосылки и
гипотезы, связывая их с тщательным содержательным экономико- теоретическим
анализом.
Разумеется, чем шире временные рамки прогнозирования банкротства , тем
очевиднее становится недостаточность простого экстраполяционного метода.
В общем случае экстраполяцию можно представить в виде формулы (11):
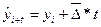 , (11)
, (11)
где 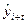 - экстраполируемый уровень
- экстраполируемый уровень
(i +t) –
номер этого уровня;
i – номер последнего уровня;
t – срок прогноза
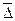 - средний абсолютный прирост.
- средний абсолютный прирост.
Однако следует иметь ввиду, что
использование среднего абсолютного прироста для прогноза банкротства возможно только при следующем условии:
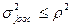 , (12)
, (12)
где:
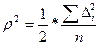 , (13)
, (13)
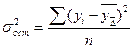 , (14)
, (14)
Например, при среднем абсолютном
приросте равном (- 0,17%), остаточной дисперсии 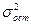 = 0,003 и
= 0,003 и 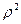 = 0,02, имеем прогноз:
= 0,02, имеем прогноз:
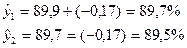
Прогнозирование по среднему темпу
роста осуществляется в случае, когда есть основание считать, что общая
тенденция ряда характеризуется показательной кривой. Для нахождения тенденции
необходимо определить средний коэффициент роста, возведенный в степень,
соответствующую периоду экстраполяции, то есть по формуле (15):
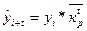 (15)
(15)
где yi- последний уровень ряда динамики;
t – срок прогноза;
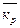 - средний коэффициент роста.
- средний коэффициент роста.
Наиболее распространенным методом
прогнозирования банкротства является
аналитическое выражение тренда. При этом для выхода за границы исследуемого
периода достаточно продолжить значения независимой переменной времени (t)[6, с. 89].
При таком подходе к прогнозированию банкротства предполагается, что размер уровня,
характеризующего явление, формируется под воздействием множества факторов,
причем не представляется возможным выделить отдельно их влияние. В связи с этим
ход развития связывается не с какими- либо конкретными факторами, а с течением
времени, то есть y= f(x).
Экстраполяция дает возможность
получить точечное значение прогноза банкротства. Точное совпадение фактических
данных и прогностических точечных оценок, полученных путем экстраполяции
кривых, характеризующих тенденцию, имеет малую вероятность.
Любой статистический прогноз
банкротства носит приближенный характер.
Поэтому целесообразно определение доверительных интервалов прогноза
банкротства.
Величина доверительного интервала
определяется следующим образом:
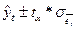 , (16)
, (16)
где 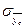 - средняя квадратическая ошибка тренда;
- средняя квадратическая ошибка тренда;
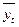 - расчетное
значение уровня;
- расчетное
значение уровня;
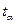 - доверительная
величина
- доверительная
величина
При прогнозировании банкротства иногда приходится прибегать к определению
неизвестных уровней внутри данного ряда динамики, то есть к интерполяции.
Как и экстраполяция, интерполяция
может производиться на основе абсолютного
прироста, среднего темпа и с помощью аналитического выравнивания. Она также
основана на том или ином предположении о тенденции изменения уровней, но
характер этого прогноза несколько иной: здесь уже не приходится предполагать,
что тенденция, характерная для прошлого, сохранится и в будущем.
При
интерполяции считается, что выявленная тенденция, ни ее характер не
претерпели существенных изменений в том промежутке времени, уровень которого
нам не известен. Такое предположение обычно является более обоснованным, чем
предположение о будущей тенденции.
2.3. Особенности метода прогнозирования
банкротства на основе тренда и
колеблемости
Одним из наиболее распространенных методов
прогнозирования банкротства является расчет прогнозов на основе тренда и
колеблемости, о котором мы уже говорили. В данной главе остановимся на этом
методе более подробно[6, с. 360].
Если мы будем знать, как быстро и в каком
направлении изменились уровни какого- либо признака, то сможем узнать какого
значения достигнет уровень через известное время. Методика статистического
прогноза банкротства по тренду и
колеблемости основана на их экстраполяции, то есть на предположении, что параметры тренда и
колеблемости сохраняются до прогнозируемого периода. Такая экстраполяция
справедлива, если система развивается эволюционно в достаточно стабильных
условиях.
Прогноз по тренду учитывает факторы только в неявном виде, что не позволяет проигрывать
разные варианты прогнозов
банкротства при разных возможных значениях
факторов, влияющих на изучаемый признак.
Рассмотрим методику прогноза банкротства (уровня банкротства) по тренду за несколько лет по конкретному
предприятию.
Итак, уравнение тренда имеет вид 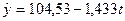 , оценка отклонения от
генеральной величины среднего квадратического отклонения от тренда s(t) = 9,45.
, оценка отклонения от
генеральной величины среднего квадратического отклонения от тренда s(t) = 9,45.
Прежде всего, вычислим точечный прогноз- значение
уровня тренда при подстановке в его уравнение номера 1998 года, считая от 1987
года, то есть tк
= 11:
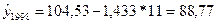
Это означает, что наиболее вероятное значение уровня банкротства в 1998 году составит около 89 % к
значению уровня банкротства
предприятия 1990 года, принятому за 100
%. Однако, параметры тренда. полученные по ограниченному числу уровней ряда -
это лишь выборочные средние оценки, не свободные от влияния распределения
колебаний отдельных уровней во времени. При изменении базы расчета тренда,
если, скажем, взять 1977- 1993 годы или 1981- 1997 годы, были бы получены
несколько иные значения параметров, а значит, и другие значения 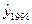 . Прогноз банкротства
должен иметь вероятностную форму, как всякое суждение о будущем.
. Прогноз банкротства
должен иметь вероятностную форму, как всякое суждение о будущем.
Средняя ошибка прогноза банкротства положения линейного тренда на год
с номером tк
вычисляется по формулам:
1)
для однократного выравнивания:
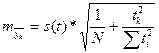 , (17)
, (17)
где tк – номер года прогноза;
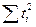 - по всей длине ряда N, то есть
- по всей длине ряда N, то есть 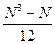
2)
для многократного скользящего выравнивания при l сдвигах базы и длине ее n:
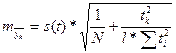 , (18)
, (18)
При N = 17, n
= 11, l = 7 имеем:
-
для однократного выравнивания 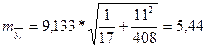
-
для многократного выравнивания 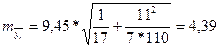
Как видим, метод многократного выравнивания на «0 % снизил среднюю ошибку
прогноза банкротства положения тренда.
Для получения достаточно надежных границ прогноза положения тренда,
скажем, с вероятностью 0,9 того, что
ошибка будет не более указанной, следует среднюю ошибку умножить на величину
критерия Стьюдента при указанной вероятности ( или значимости 1- 0,9 = 0,1) и
при числе степеней свободы, равном, для линейного тренда, N- 2 , то есть 15. Эта величина равна
1,753. Получаем предельную с данной вероятностью ошибку:
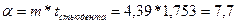
Следовательно, с вероятностью 0,9 можно ожидать, что уровень банкротства в 1998 году пройдет между значениями 88,77 +
7,70 и 88,77 – 7,70; от 81,07 до 96,47 в процентах к уровню банкротства
предприятия 1990.
Однако, фактические уровни отклоняются от тренда. Уровень банкротства в 1998 году также может быть
вовсе не равен уровню положения тренда в этом году. Ошибка прогноза
банкротства конкретного уровня включает две неопределенности: во- первых, мы
не знаем точно, где окажется тренд в 1998 году, а во- вторых- в какую сторону и
на сколько уровень банкротства ряда отклонится
в 1998 году от положения тренда. Считая, как уже было сказано, колебания
случайно распределенными во времени, то есть независимыми от тренда, определим
ошибку прогноза уровня банкротства конкретного года по правилу сложения
независимых дисперсий.
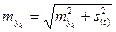 , (19)
, (19)
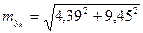 = 10,42
= 10,42
С вероятностью 0,9 ошибка прогноза уровня
банкротства не превзойдет
величины 18,27 (10,42* 1,753) и доверительные границы прогноза банкротства составят от 70,5 до 107 % к уровню 1990 года.
Как видим, точность прогноза
банкротства невелика, разброс
возможных значений достиг 37 пунктов, а вероятная ошибка составила 0,206 ил
20,6 % от средней величины (точечного прогноза банкротства ). Можно уменьшить
значение вероятной ошибки, если сделать прогноз с меньшей надежностью, скажем с
вероятностью 0,75. Тогда значение критерия Стьюдента составит 1,197, вероятная
ошибка составит 12,47 пункта, доверительные границы – от 76,3 до 101,24 % к
уровню 1990 года. За уменьшение вероятной ошибки, однако, пришлось заплатить
снижением надежности прогноза.
Таким образом, методика анализа и прогнозирования определяет степень
полноты извлечения информации, содержащейся в исходном ряду динамики. С помощью
методики многократного выравнивания удается более полно извлечь информацию о
тренде и уменьшить среднюю ошибку прогноза положения в прогнозируемом периоде с
5,44 до 4,39. Однако, главной
составляющей ошибки прогноза конкретного уровня в нашем расчете является
не ошибка прогноз положения тренда, а колеблемость уровней вокруг тренда.
Поэтому ошибка прогноза банкротства
конкретного уровня незначительно сократилась за счет многократного
выравнивания. При слабой колеблемости уровней и прогнозировании
банкротства на значительное удаление от
базы, главную роль станет играть ошибка положения тренда. Тогда многократное
выравнивание даст значительное сокращение средней ошибки прогноза
банкротства конкретных уровней. Но в
любом случае эта ошибка всегда больше показателя колеблемости уровней -
среднего квадратического отклонения.
2.4. Прогнозирование банкротства на основе
модели Альтмана
Полученная в результате технико-экономического анализа деятельности
предприятий система показателей позволяет выявить слабые места
в экономике предприятия, охарактеризовать состояние дел данного
предприятия (его ликвидность, финансовую устойчивость, рентабельность, отдачу
активов и так далее).
Однако, на основе такого анализа сделать вывод, что данное предприятие
обанкротиться или, наоборот, выживет обычно невозможно. Выводы о вероятности
банкротства можно сделать только на основе сопоставления показателей данного
предприятия и аналогичных предприятий, обанкротившихся или, наоборот,
избежавших банкротства. Однако подыскать в каждом случае подходящий аналог не
всегда представляется возможным или такого аналога вообще может не
существовать.
Задача прогнозирования банкротства может быть решена методом дискриминантного
анализа. Последний представляет собой раздел факторного статистического
анализа, с помощью которого решаются
задачи классификации, то есть разбиения некоторой совокупности анализируемых
объектов на классы путем построения так называемой классифицирующей функции в
виде корреляционной модели.
В основе зарубежной практики диагностики угрозы банкротства лежит модель
Альтмана, или Z-счет
Альтмана. Модель Альтмана определяет интегральный показатель угрозы
банкротства. В основе расчета лежит пятифакторная модель, представляющая
комплексный коэффициентный анализ. Альтман определил коэффициенты значимости
отдельных факторов в интегральной оценке вероятности банкротства. Модель
Альтмана имеет следующий вид:
Z=0,012X1+0,014X2+0,033X3+0,006X4+0,999X5, (20)
где Z- интегральный показатель уровня угрозы банкротства;
X1-отношение собственных оборотных активов (чистого
оборотного капитала) к сумме активов;
X2- рентабельность активов (нераспределенная прибыль к
сумме активов);
X3- отношение прибыли к сумме активов;
X4-
коэффициент соотношения собственного и заемного капитала;
X5-
оборачиваемость активов, или отношение выручки от реализации к сумме активов.
Если коэффициенты принимаются в виде долей, то формула (20) будет иметь
вид:
Z=1,2X1+1,4X2+3,3X3+0,6X4+1,0X5, (21)
Зона неведения находится в интервале от 1,81 до 2,99. Чем больше значение
Z, тем меньше
вероятность банкротства в течение двух лет.
Уровень угрозы банкротства в модели Альтмана оценивается согласно таблице
2.
Таблица
2
Оценка
уровня угрозы банкротства в модели Альтмана
|
Значение
Z
|
Вероятность
банкротства
|
|
Менее
1,81
|
очень
высокая
|
|
От
1,81 до 2,7
|
высокая
|
|
От
2,7 до 2,99
|
вероятность
невелика
|
|
Более
2,99
|
вероятность
ничтожна, очень низкая
|
Эта модель применима в условиях России только для акционерных обществ,
акции которых свободно продаются на рынке ценных бумаг, то есть имеют рыночную
стоимость. Поэтому вместо модели Альтмана иногда целесообразно использовать
двухфакторную модель в части прогнозирования вероятности банкротства. Для этого
выбирают два ключевых показателя, от которых зависит вероятность банкротства
организации, например, показатель текущей ликвидности и удельного веса заемных
средств в активах. Они умножаются на соответствующие постоянные весовые
коэффициенты[3, с. 37].
Предположим, что факт банкротства определяют два показателя: коэффициент
покрытия, то есть отношение текущих активов к краткосрочным обязательствам, и
коэффициент финансовой независимости, то есть отношение заемных средств к общей
стоимости активов.
Первый показатель характеризует
ликвидность, второй - финансовую устойчивость. Очевидно, что при прочих
равных условиях вероятность банкротства тем меньше, чем больше коэффициент
покрытия и меньше коэффициент финансовой зависимости. И, наоборот, предприятие
наверняка станет банкротом при низком коэффициенте покрытия высоком
коэффициенте финансовой зависимости. Задача состоит в том, чтобы найти
эмпирическое уравнение некой дискриминантной
границы, которая разделит все возможные сочетания указанных показателей
на два класса[4, с. 46]:
1)
сочетания показателей, при которых предприятие
обанкротится;
2)
сочетания показателей, при которых предприятию
банкротство не грозит.
Данная задача была решена американским экономистом Э. Альтманом. За
определенный период были собраны данные о финансовом состоянии 19 предприятий.
По указанным двум показателям положение предприятий было неустойчивым: одна
половина предприятий обанкротилась, а другая - смогла выжить. Далее приемами
дискриминантного анализа рассчитывались параметры корреляционной линейной
функции, описывающей положение дискриминантной границы между двумя классами
предприятий:
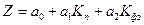 , (22)
, (22)
где Z- показатель
классифицирующей функции
a0 – постоянный
параметр
a1 – параметр, показывающий степень влияния
коэффициента покрытия на вероятность
банкротства
Кп – коэффициент покрытия
а2 – параметр, показывающий
степень влияния коэффициента финансовой зависимости на вероятность банкротства
Кфз – коэффициент финансовой
зависимости
В результате статистической обработки
данных была получена следующая корреляционная зависимость[2,c.50]:
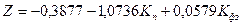 , (23)
, (23)
При Z = 0 имеем
уравнение дискриминантной границы. Для предприятий, у которых Z = 0, вероятность обанкротиться 50 %.
Для предприятий, у которых Z
< 0, вероятность банкротства меньше 50 % и далее снижается по мере уменьшения
Z. Если Z > 0, то вероятность
банкротства больше 50 % и возрастает с
ростом Z.
Знаки параметров а1 и а2 классифицирующей функции
связаны с характером влияния соответствующих показателей. Параметр а1
имеет знак «минус», поэтому чем больше
коэффициент покрытия, тем меньше показатель Z и тем меньше вероятность банкротства предприятия. В то же время
параметр а2 имеет знак «плюс», поэтому чем выше коэффициент
финансовой зависимости, тем больше Z и , следовательно, выше
вероятность банкротства предприятия [1, с. 156].
Рассмотрим методику применения двухфакторном модели Альтмана на
конкретном примере.
Исходные данные для расчета представлены в таблице 3.
Таблица 3
Исходные данные и результаты расчеты вероятности банкротства
предприятий
|
Номер предприятия
|
Коэффициент покрытия,
%
|
Коэффициент финансовой
независимости, %
|
Показатель Z
|
Вероятность
банкротства, %
|
Фактическое положение
|
|
1
|
3,6
|
60
|
-0,78
|
17,2
|
Нет
|
|
2
|
3,0
|
20
|
-2,451
|
0,8
|
Нет
|
|
3
|
3,0
|
60
|
-0,135
|
42
|
Нет
|
|
4
|
3,0
|
76
|
0,791
|
81,8
|
Да
|
|
5
|
2,8
|
44
|
-1,841
|
15,5
|
нет
|
|
6
|
2,6
|
56
|
0,062
|
51,5
|
Да
|
|
7
|
2,6
|
68
|
0,757
|
80,2
|
Да
|
|
8
|
2,4
|
40
|
-0,649
|
21,1
|
Да
|
|
9
|
2,4
|
60
|
0,509
|
71,5
|
нет
|
|
10
|
2,2
|
28
|
-1,129
|
9,6
|
нет
|
|
11
|
2,0
|
40
|
-0,221
|
38,1
|
нет
|
|
12
|
2,0
|
48
|
0,244
|
60,1
|
нет
|
|
13
|
1,8
|
60
|
1,153
|
89,7
|
Да
|
|
14
|
1,6
|
20
|
-0,948
|
13,1
|
нет
|
|
15
|
1,6
|
44
|
0,441
|
68,8
|
Да
|
|
16
|
1,2
|
44
|
0,871
|
83,5
|
Да
|
|
17
|
1,0
|
24
|
-0,072
|
45
|
нет
|
|
18
|
1,0
|
32
|
0,391
|
66,7
|
Да
|
|
19
|
1,0
|
66
|
2,012
|
97,9
|
Да
|
В силу того, что двухфакторная модель не полностью описывает финансовое
положение предприятия, расчетные и фактические показатели могут расходиться.
Предприятие 8 имело Z =
-0,649, то есть не должно было бы обанкротиться (вероятность банкротства около
20 %), в действительности же потерпело банкротство. В то же время предприятия 9
и 12 имели положительные значения Z, но они сумели избежать
банкротства.
На рисунке 2 представлено корреляционное поле и положение на нем
дискриминантной линии для двух показателей – коэффициента покрытия и коэффициента
финансовой зависимости.



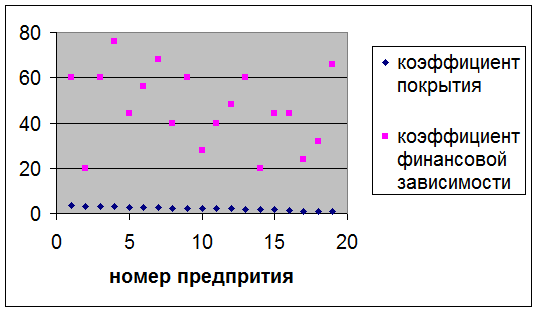
Рис. 2. Дискриминантная линия на корреляционном поле
показателей покрытия и финансовой устойчивости.
Из рисунка 2 видно, что предприятия, у которых значения показателей
коэффициента покрытия и коэффициента финансовой независимости располагаются
ниже и правее дискриминантной линии, вероятнее всего обанкротятся (вероятность
их банкротства превышает 50 %). При этом, чем дальше отстоит точка показателей от дискриминантной линии,
тем выше вероятность банкротства. Для предприятий, у которых сочетание значений
показателей финансовой устойчивости и покрытия находится выше и левее
дискриминантной линии, почти нет угрозы банкротства. Например, точка 2
расположена над дискриминантной линией и достаточно далека от нее; она отражает
состояние предприятия 2, у которого коэффициент покрытия равен 3, а коэффициент
финансовой зависимости равен 20 %.
Предприятие 19 имеет высокую вероятность банкротства (около 98 %), и оно
действительно обанкротилось.
Выше отмечалось, что по практическим данным установлены значения для
коэффициента покрытия не ниже единицы, а для коэффициента финансовой
зависимости не выше 50 %. Если
подставить приведенную выше двухфакторную модель Альтмана эти значения (Кп = 1
и Кфз = 50 %), то получим Z
= 1,, то есть почт с 90- процентной вероятностью можно утверждать, что такое
предприятие в российских условиях обязательно обанкротится.
Прогнозирование банкротства с использованием двухфакторной модели в
российских условиях не обеспечивает высокой точности. это объясняется тем, что
данная модель не учитывает влияния на финансовое состояние предприятия других
важнейших факторов и показателей, характеризующих, например, рентабельность,
отдачу активов, деловую активность предприятия и так далее [9, с. 67].
Дискриминантная граница между банкротами
и небанкротами имеет вид не тонкой линии, а размытой полосы. Ошибка прогноза с
помощью двухфакторной модели оценивается интервалом Δ Z = 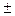 0,65. Чем больше
факторов будет учтено в модели, тем, естественно, точнее рассчитанный с ее
помощью прогноз.
0,65. Чем больше
факторов будет учтено в модели, тем, естественно, точнее рассчитанный с ее
помощью прогноз.
При использовании модели Альтмана возможны два типа ошибок[8, с. 156]:
-
прогнозируется сохранение платежеспособности
предприятия, а в действительности происходит банкротство;
-
прогнозируется банкротство предприятия, а оно сохраняет
платежеспособность.
По мнению Альтмана, с помощью пятифакторной модели прогноз банкротства на
горизонте один год можно установить с точностью до 95 %. При этом ошибка
первого типа возможна в 6 %, а ошибка второго типа - в 3 %случаев.
Спрогнозировать банкротство на горизонте в 2 года удается с точностью до 83 %,
при этом ошибка первого рода имеет место в 28 % случаях, а ошибка второго рода
имеет место в 6 % случаев.
В 1977 году Альтман со своими коллегами разработал более точную семи
факторную модель. Эта модель позволяет спрогнозировать банкротство на горизонте
в 5 лет с точностью до 70 %. В модели в качестве переменных используются
следующие показатели[10, с. 178]:
-
рентабельность
активов;
-
изменчивость или динамика прибыли;
-
коэффициент покрытия процентов по кредитам;
-
кумулятивная прибыльность;
-
коэффициент покрытия или ликвидности;
-
коэффициент автономии;
-
совокупные активы.
В таблице 4 приведены сведения о точности прогнозирования банкротства с
помощью пятифакторной и семи факторной модели Альтмана.
Таблица 4
Точность прогноза банкротства
|
Количество
лет до банкротства
|
Прогноз
по пятифакторной модели
|
Прогноз
по семи факторной модели
|
|
Банкрот
|
Небанкрот
|
Банкрот
|
Небанкрот
|
|
1
|
93,9
|
97
|
96,2
|
89,7
|
|
2
|
71,9
|
93,9
|
84,9
|
93,1
|
|
3
|
48,3
|
-
|
74,5
|
91,4
|
|
4
|
28,6
|
-
|
68,1
|
89,5
|
|
5
|
36
|
-
|
69,8
|
82,1
|
При проведении финансового анализа практически к любому оценочному
показателю нужно подходить критически. Вместе с тем значение показателя Z следует воспринимать как
сигнал опасности. В этом случае необходим глубокий анализ причин, вызвавших
снижение этого показателя.
Таким образом, разработанные на Западе модели прогнозирования вероятности
банкротства весьма применимы и в современных российских условиях, но тем не
менее, имеют ряд особенностей и характерных черт.
2.5.
Метод экспертных оценок
Методы экспертных оценок вероятности
банкротства, которые предусматривают многоступенчатый опрос
экспертов по специальным схемам и обработку полученных результатов с помощью
инструментария экономической статистики. Это наиболее простые и достаточно
популярные методы, история которых насчитывает не одно тысячелетие. Применение
этих методов на практике, обычно, заключается в использовании опыта и знаний
торговых, финансовых, производственных руководителей предприятия. Как правило,
это обеспечивает принятие решения наиболее простым и быстрым образом. Недостатком
является снижение или полное отсутствие персональной ответственности за
сделанный прогноз. Экспертные оценки применяются не только для прогнозирования
значений показателей, но и в аналитической работе, например, для разработки
весовых коэффициентов в модели Альтмана, пороговых значений контролируемых показателей
и т. п.
Этот метод используется если нет статистической базы по
возможным исходам интересующих событий. Суть метода в следующем:
составляется группа людей с информацией
по интересующему вопросу прогнозирования вероятности банкротства
предприятия. С помощью специальных
приемов отбираются эксперты в пределах 11- 12 человек. Если количество человек
больше или меньше, то возможно появление
ошибки мнения эксперта. Перед выбранными экспертами стоит задача выполнить оценку по
прогнозному показателю
вероятности банкротства предприятия. В общем случае процесс согласованности
оценки мнений эксперта и получение этой оценки включает следующее:
-
группировка и агрегирование признаков (постановка
задач);
-
согласованность, оценка степени согласованности
ответственности экспертов по каждому признаку в отдельности и в целом по всему
набору;
-
выделение групп
экспертов с близким мнением
относительно порядка признаков в случае
наличия существенных расхождений в
ответах
 количество экспертов
количество экспертов
 7 10
7 10
 5
5
 а1 а2 а3 а4 а5 а6
оценка банкротства
а1 а2 а3 а4 а5 а6
оценка банкротства
Рис.
3. Зависимость оценки банкротства и
количества экспертов , давших оценку показателю
-
выявление причин
разброса мнений, определение влияния компетентности других качеств
экспертов на содержание ответов;
-
качество экспертных оценок и компетентности эксперта;
-
формированием группового решения.
Для оценки разбросанности и
согласованности оценок, полученных от эксперта, применяют обобщенные
статистические характеристики: средние и меры разброса. Можно вычислить
интерквантильную вариацию (24):
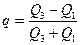 , (24)
, (24)
где q – коэффициент интерквантильной вариации,
Q1,Q3
- квартиль- статистическая величина
Считается, что мнения совпадают
хорошо, если этот коэффициент принимает значение большее 0,7, мнения
удовлетворительно совпадают, если коэффициент
между 0,4 и 0,7, мнения значительно разбросаны, если коэффициент меньше 0,4.
Далее рассчитывается групповая
экспертная оценка по формуле (25):
ГЭО
= а + Δ, (25)
где ГЭО – групповая экспертная оценка,
а – среднее значение оценок экспертов,
Δ – нормально распределенная случайная величина.
 вероятность
вероятность
 -Δ а +Δ оценка
-Δ а +Δ оценка
Рис.
4. Групповая экспертная прогнозная
оценка вероятности банкротства
2.6. Метод построения прогнозной отчетности
Проведение анализа вероятности банкротства
непосредственно по данным бухгалтерской
отчетности - дело довольно трудоемкое, так как слишком большое количество
расчетных показателей не позволяет выделить главные тенденции в финансовом
состоянии организации при оценке вероятности банкротства. Еще более
неэффективным представляется прогнозирование форм бухгалтерской отчетности в их
типовой номенклатуре статей. В связи с этим возникает необходимость перед
проведением анализа вероятности банкротства предприятия уплотнить исходные
формы отчетности путем агрегирования однородных по составу балансовых статей
для получения сравнительного аналитического баланса (баланса-нетто), а также
аналитического отчета о прибылях и убытках.
Кроме того, современная отчетность
большинства предприятий не удовлетворяет требованию временной сопоставимости
данных, так как структура отчетных форм неоднократно менялась. Данное
требование к отчетности чрезвычайно важно, так как все рассчитанные по ее
данным аналитические показатели будут бесполезны, если не будет возможно их
сравнение в динамике. И, конечно же, в этом случае будет невозможно
спрогнозировать финансовое состояние предприятия даже на ближайшую перспективу.
В свете вышесказанного становится ясным, что анализ и прогнозирование,
базирующиеся на российской бухгалтерской отчетности, становятся возможными
только после приведения данных за разные годы к какому-то единому
аналитическому виду. При этом преобразование исходных форм бухгалтерской
отчетности в аналитические формы единого вида можно рассматривать как
необходимый первый шаг предварительного этапа, предшествующего проведению
анализа и прогнозирования финансового состояния предприятия при оценке вероятности банкротства.
Структура аналитических форм отчетности, степень агрегирования статей и
перечень процедур ее формирования определяются аналитиком и зависят от целей
анализа (в данном случае - оценка вероятности банкротства предприятия). Следует
иметь в виду, что уровень агрегирования данных определяет степень аналитичности
отчетности. Причем связь здесь обратно пропорциональна: чем выше уровень
агрегирования, тем меньше пригодны для анализа отчетные формы[1, с. 158].
При трансформации в сравнительный аналитический баланс исходный
баланс уплотняется, т.е.
представляется в виде агрегированного
сравнительного аналитического баланса, в котором информация отдельных
однородных статей бухгалтерского баланса объединена в группы. Основой
группировки статей актива баланса являлась степень их ликвидности и
материально-вещественной формы, для пассива - отнесение к собственным и заемным
источникам формирования имущества, а в рамках последнего - срочность возврата.
Первой строкой актива аналитического баланса является строка "Внеоборотные
активы", получаемая как итог первого раздела бухгалтерского баланса.
Вторая часть - "Текущие активы" состоит из статей раздела
"Оборотные активы" бухгалтерского баланса, сгруппированных по степени
их ликвидности в три группы: наиболее ликвидные активы, быстрореализуемые
активы и медленнореализуемые активы. Медленнореализуемые активы, в свою
очередь, делятся на запасы и прочие медленнореализуемые активы. Пассив
аналитического баланса состоит, во-первых, из собственного капитала,
определяемого как итог четвертого раздела бухгалтерского баланса "Капитал
и резервы". Кроме того, в пассивной части баланса представлены кредиты и
займы, делящиеся на краткосрочные (срок погашения в течение 12 месяцев) и
долгосрочные (подлежащие погашению более чем через 12 месяцев). При этом по
строке "Долгосрочные кредиты и займы" отражались также и прочие
долгосрочные пассивы. Последняя строка аналитического баланса
"Кредиторская задолженность" содержит в себе величины кредиторской
задолженности и прочих краткосрочных пассивов из исходной Формы №1.
Аналитический отчет о прибылях и убытках состоит из двух строк - "Выручка
от реализации" и "Чистая прибыль". Это первая и последняя строки
из формы №2 бухгалтерской отчетности. Таким образом, аналитический отчет
включает в себя только исходный фактор (выручка) и результативный показатель
(чистая прибыль), в отличие от бухгалтерского отчета, содержащего и все
промежуточные факторы, влияющие на определение результата.
При проведении расчетов аналитические формы отчетности легко получаются
из бухгалтерских форм с применением персональной ЭВМ. Для этих целей
использовался программный продукт Audit Expert компании Про-Инвест-ИТ.
Реализованный в этом продукте сценарный подход позволяет автоматически привести
данные за различные периоды к единой описанной выше аналитической форме. Также
с помощью Audit Expert на основании полученных аналитических форм отчетности
рассчитывается система показателей, характеризующих финансовое состояние
предприятия, а именно показатели ликвидности и платежеспособности,
устойчивости, рентабельности и деловой активности предприятия, которые в
дальнейшем используются при оценке вероятности банкротства предприятия.
Практическая часть
УСЛОВИЕ ЗАДАЧИ
Проанализировать динамику и структуру
дебиторской и кредиторской задолженности предприятия. Проанализировать
структуру баланса предприятия и сделать выводы о вероятности наступления
кризисной ситуации. Темп инфляции за квартал равен – 7 %.
РЕШЕНИЕ
Таблица 5
Динамика структуры
дебиторской задолженности
|
Показатель
|
01.01.1997
|
01.04.1997
|
01.07.1997
|
01.10.1997
|
|
тыс. руб.
|
%
|
тыс. руб.
|
%
|
тыс. руб.
|
%
|
тыс. руб.
|
%
|
|
Расчеты с дебиторами
за товары, работы и услуги
|
2
|
1,1
|
10
|
2,9
|
480
|
64,7
|
4170
|
77,7
|
|
Расчеты с дочерними предприятиями
|
0
|
0,0
|
0
|
0,0
|
15
|
2,0
|
1
|
0,0
|
|
Расчеты с бюджетом
|
50
|
27,5
|
26
|
7,4
|
26
|
3,5
|
100
|
1,9
|
|
Расчеты с персоналом
|
2
|
1,1
|
2
|
0,6
|
1
|
0,1
|
1
|
0,0
|
|
Расчеты с прочими дебиторами
|
128
|
70,3
|
312
|
89,1
|
220
|
29,6
|
1097
|
20,4
|
|
ИТОГО
|
182
|
100,0
|
350
|
100,0
|
742
|
100,0
|
5369
|
100,0
|
На рисунке 5 отражена динамика основных
расчетов с дебиторами организации за
1997 год.
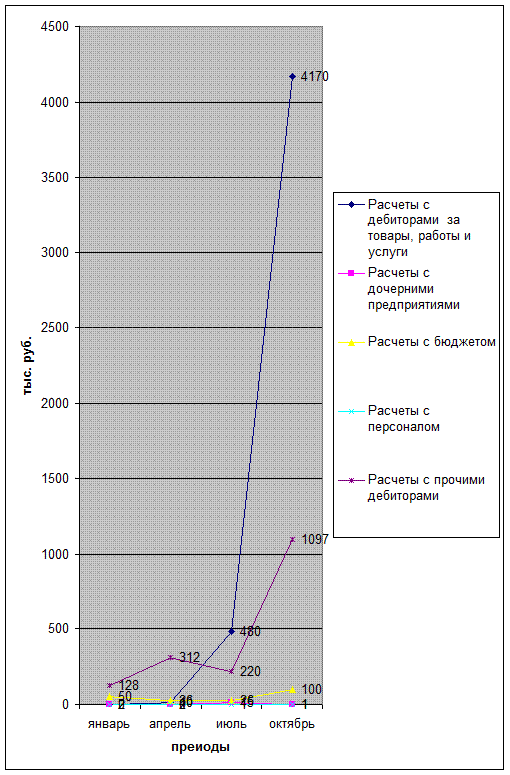
Рис.5.
Динамика основных расчетов с дебиторами организации в 1997 году, тыс. руб.
Как видно из рисунка 5, в 1997 году в
организации наблюдались следующие тенденции всех значений расчетов с дебиторами:
- за товары и
услуги рост с 2 до 480 тыс. руб.;
- с дочерними
предприятиями рост с 0 до 1 тыс. руб.;
- с бюджетом
снижение с 50 до 26 тыс. руб.;
- с персоналом – снижение с 2 до 1 тыс. руб.
- с прочими
дебиторами - рост с 128 до 220 тыс. руб.
На рисунке 6 отражена динамика
структуры расчетов с дебиторами в 1997
году по организации.
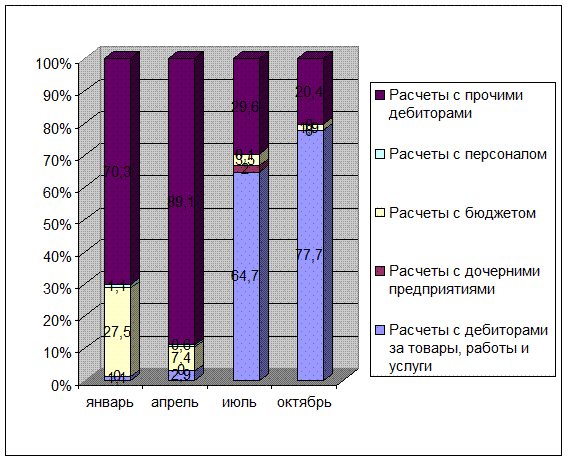
Рис.
6. Динамика структуры расчетов с дебиторами организации
Как видно из рисунка 6, на 01.01.97
организации наибольшую долю в структуре расчетов с дебиторами занимали расчеты с прочими дебиторами (70,3 %), а
наименьшую – расчеты за товары и услуги- 1.1 % и расчеты с персоналом – 1.1 %. Расчеты с дочерними
предприятиями вообще отсутствовали.
На 01.04.97 наибольшую долю в структуре
расчетов с дебиторами занимали расчеты с прочими дебиторами (89,1 %), а наименьшую – расчеты с
персоналом – 0,6 %, расчеты с дочерними организациями отсутствовали.
На 01.07.04 в структуре расчетов дебиторами наибольшую долю занимали
расчеты за товары и услуги – 64,7 %,
затем идут – расчеты с прочими дебиторам – 29,6 %, а наименьшую – расчеты с
персоналом – 0,1 %. Появились расчеты с
дочерними предприятиями ( 2 %).
На 01.10.97 наибольшую долю в структуре
расчетов с дебиторами занимали расчеты
за товары услуги- 77,7 %, а наименьшую-
расчеты с дочерними предприятиями (менее 0,01 %). Исчезли расчеты с персоналом (0 %).
В таблице 6 отражена динамика расчетов с кредиторами организации в 1997 году
Таблица
6
Динамика
расчетов с кредиторами организации в
1997 году
|
Показатель
|
01.01.1997
|
01.04.1997
|
01.07.1997
|
01.10.1997
|
|
тыс. руб.
|
%
|
тыс. руб.
|
%
|
тыс. руб.
|
%
|
тыс. руб.
|
%
|
|
Расчеты с кредиторами за товары и услуги
|
1297
|
56,4
|
1727
|
43,1
|
1456
|
45,4
|
3115
|
64,5
|
|
Расчеты по оплате труда
|
289
|
12,6
|
474
|
11,8
|
292
|
9,1
|
379
|
7,8
|
|
Расчеты по социальному страхованию и обеспечению
|
132
|
5,7
|
160
|
4,0
|
200
|
6,2
|
200
|
4,1
|
|
Расчеты по внебюджетным платежам
|
42
|
1,8
|
55
|
1,4
|
51
|
1,6
|
86
|
1,8
|
|
Расчеты с бюджетом
|
326
|
14,2
|
548
|
13,7
|
530
|
16,5
|
288
|
6,0
|
|
Расчеты с прочими кредиторами
|
213
|
9,3
|
1041
|
26,0
|
678
|
21,1
|
761
|
15,8
|
|
ИТОГО
|
2299
|
100,0
|
4005
|
100,0
|
3207
|
100,0
|
4829
|
100,0
|
На рисунке 7 отражена динамика значений расчетов с кредиторами организации в
1997 году
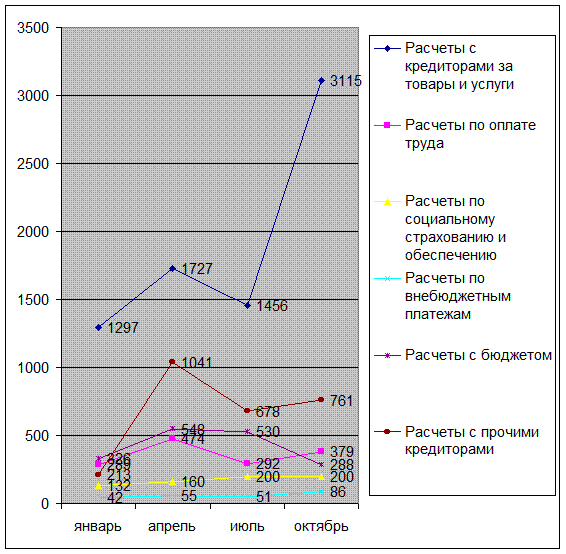
Рис.
7. Динамика расчетов с кредиторами организации в 1997 году, тыс. руб.
Как видно из рисунка 7, в организации в
1997 году заметны следующие тенденции:
- расчеты за товары и услуги с кредиторами выросли с 1297 до 31115 тыс. руб.:
- расчеты с кредиторам по оплате труда выросли с 289 до 379 тыс. руб.;
- расчеты с кредиторами по социальному страхованию выросли с 132 до 200 тыс. руб.;
- расчеты по внебюджетным платежам выросли с 42 до 86 тыс. руб.;
- расчеты с
бюджетом упали с 326 до 288 тыс. руб.;
- расчеты с
прочими кредиторами выросли с 213 до 761 тыс. руб.
Таким образом, все расчеты с
кредиторами организации выросли за исключением расчетов с бюджетом.
На рисунке 8 отражена динамика
структуры расчетов с кредиторами организации в 1997 году.
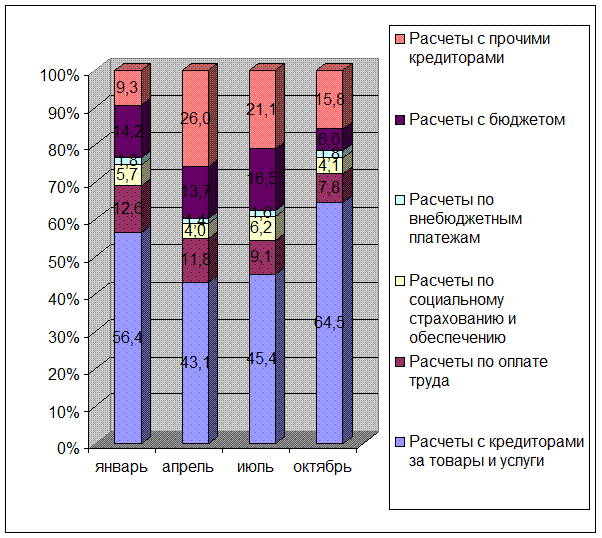
Рис.
8. Динамика структуры расчетов с
кредиторами организации в 1997 году
Как видно из рисунка 8, в 1997 году наблюдались
следующие тенденции
- на 01.01. 97 наибольшую долю в структуре
расчетов с кредиторами занимали расчеты
за товары и услуги – 56,4 %, а наименьшую – расчеты по внебюджетным платежам- 1,8 %;
- на 01.04.97
наибольшую долю в структуре расчетов с кредиторам занимали расчеты за товары и услуги – 43,1 %, а наименьшую
- по внебюджетным платежам- 1,4 %:
- на 01.07.97
наибольшую долю в структуре расчетов занимали расчеты за товары – 45,4 %, а наименьшую –
расчеты по внебюджетным платежам- 1,6 %;
- на 01.10.97
наибольшую долю в структуре расчетов занимали расчеты за товары и услуги – 64,5
%, а наименьшую – расчеты по
внебюджетным платежам- 4,1 %.
В таблице 7 представлена структура актива и пассива баланса организации
в 1997 году по периодам.
Таблица
7
Структура
баланса организации в 1997 году
|
Статья баланса
|
01.01.1997
|
01.04.1997
|
01.07.1997
|
01.10.1997
|
|
%
|
%
|
%
|
%
|
|
АКТИВ
|
|
|
|
|
|
Основные средства и внеоборотные активы
|
83,3
|
76,4
|
74,4
|
60,9
|
|
Запасы и затраты
|
8,2
|
16
|
11,6
|
20,6
|
|
Денежные средства и прочие активы
|
8,5
|
7,6
|
14
|
18,5
|
|
ИТОГО АКТИВОВ
|
100
|
100
|
100
|
100
|
|
ПАССИВ
|
|
|
|
|
|
Уставной капитал
|
77,9
|
73,3
|
73,9
|
65,6
|
|
Добавочный капитал и накопленная прибыль
|
9,4
|
9,4
|
11,2
|
9,8
|
|
Долгосрочные кредиты и займы
|
0
|
0
|
0
|
0
|
|
Краткосрочные пассивы
|
12,7
|
17,3
|
14,9
|
24,6
|
|
ИТОГО ПАССИВОВ
|
100
|
100
|
100
|
100
|
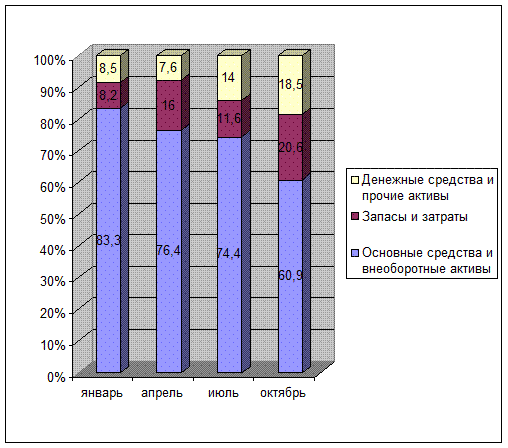
Рис.
9. Динамика структуры актива баланса организации в 1997 году
Как видно из рисунка 9:
- на 01.01. 97 в
организации наибольшую долю в структуре активов занимали основные средства- 83,3 %, а наименьшую – запасы
и затраты- 8,2 %;
- на
01.04.97 доля основных средств упала до
76,4 %, но при этом осталась наибольшей в структуре, а доля запасов и затрат выросла до 16 %, доля денежных средств уменьшилась до 7,6 %, при этом стала
минимальной;
- на
01.07.97 доля основных средств упала до
74,4 %, при этом осталась максимальной. Оля
запасов упала до 11,6 %, стала
при этом минимальной. Доля денежных
средств выросла до 14 %;
- на 01.10.97
доля основных средств упала до 60,9 %,
при этом осталась максимальной в структуре активов. Доля запасов выросла до 20,6 . Доля денежных
средств выросла до 18,5 %, при этом
осталась минимальной в активах.
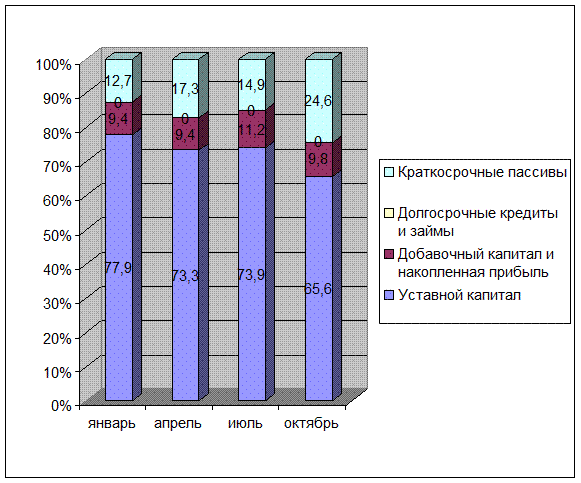
Рис.
10. Динамика структур пассива баланса организации в 1997 году
Как видно из рисунка 10:
- на
01.01.97 доля уставного капитала максимальна в
структуре пассива- 77,9 %, доля
добавочного капитала минимальна – 9,7 %;
- на 01.04.97
доля уставного капитала падет до 73,3 %, при этом оставаясь максимальной.
Доля добовочного капитала та же – 9,4%.
Доля краткосрочных пассивов растет с
12,7 до 17,3 %;
- на 01.07.97
доля уставного капитала растет до 73,9
%, оставаясь максимальной. Доля
добавочного капитала расчет до 11,2 %, оставаясь минимальной в структуре
пассива. Доля краткосрочных
пассивов падает до 14,9 %;
- на 01.10.97
доля уставного капитала падает до 65,6 %. Доля добавочного капитала падет до
9,8 %. При этом резко возрастает доля краткосрочных пассивов с 14,9 до 24,6 %.
Определим вероятность наступления кризисной
ситуации организации при использовании
двухфакторной модели Альтмана:
1)
коэффициент
покрытия или ликвидности равен
отношению суммы денежных средств
организации, дебиторской задолженности и
запасов к сумме кредиторской задолженности и краткосрочных пассивов :
дебиторская задолженность на 01.10. 97 равна 5369 тыс. руб. и
составляет 18,5 % в структуре активов.
Значит, сумма активов равна:
29022 тыс. руб.
Тогда при условии, что доля запасов равна 20,6 %, их сумма составляет:
29022 *0,206 =
5979 тыс. руб.
Общая сумма
денежных средств и запасов равна 11348 тыс. руб.
Сумма пассивов рана 29022 тыс. руб.
Сумма краткосрочных кредитов банка при доле 24,6 % равна:
29022*0,246 =
7139 тыс. руб.
Сумма кредитов банка и кредиторской
задолженности равна:
7139 +4829 =
11968 (тыс. руб.)
Коэффициент абсолютной ликвидности равен:
11348/11968 =
0,95 или 95 %
Значит, организация не в состоянии
покрыть свои обязательства имеющимися активами. Ликвидность отрицательна.
2)
Коэффициент финансовой зависимости равен отношении.
Валюты баланса к источникам собственных
средств организации:
Валюта баланса равна 29022 тыс. руб.
Источники собственных средств на
01,10.97 составляют 75,4 %от валюты баланса:
29022*0,754 =
21883 ( тыс. руб.)
Тогда
коэффициент финансовой зависимости равен:
29022/21883 =
1,33
3)
При использовании двухфакторной модели Альтмана:
Z = -0,3877
-1,0736*0,95+0,0579*1,33 = -1,33
Значит,
вероятность банкротства организации очень высокая.
Список литературы
1)
Ковалев А.И.,
Привалов В.П. Анализ финансового состояния предприятия. – 4 изд., испр., доп. –
М.: Центр экономки и маркетинга, 2000. – 208 с.
2)
Ковалев А.П. Диагностика банкротства. – М.:
Финстатинформ, 1995. – 96 с.
3)
Латушкина Н.М. Теория экономического анализа. – Тюмень:
Изд- во ТГУ, 2003. – 152 с
4)
Левин А.Е. Технико-экономический анализ деятельности
организаций: Учеб. пособ. – М.: МИКХиС, 2002. – 56с
5)
Прогнозирование и планирование: Учеб. пособ./ Е.А. Черныш, О.П. Молчанова, А.А.
Новикова, Т.А.Салтанова. – М.: Приор, 1999. – 176 с.
6)
Пястолов С.М. Анализ финансово- хозяйственной
деятельности предприятия: Учеб. – М.: Мастерство, 2001. – 336 с.
7)
Справочное пособие директору производственного
объединения (предприятия) В 2 т./ Под ред. Е.А.Егиазаряна и А.Д. Шеремета. – М.
: Экономика, 1997
8)
Статистика финансов: Учеб./ Под ред. В.Н. Салина. – М.:
Финансы и статистика, 2000. – 816 с.
9)
Теория статистики с основами теории вероятности: Учеб.
пособ./ И.И. Елисеева, В.С. Князевский, Л.И. Ниворожнина, З.А. Морозова. – М.:
Юнити- Дана, 2001 .- 446 с
10)
Шеремет А.Д., Сайфулин Р.С. Финансы предприятия. – М.:
Инфра- М, 1997. - 343 с.
11)
Шеремет А.Д., Сайфулин Р.С. Методика финансового
анализа. – М.: Инфра- М, 1996. – 176 с.
12)
Финансы: Учеб.- М.: ИД ФБК-Пресс, 2000. – 760 с.
13)
Черкасова И.О. Анализ хозяйственной деятельности. –
СПб.: Нева, 2003. – 192 с.
14)
Четыркин Е.М. Статистические методы прогнозирования. –
М.: Статистика, 1995. – 278 с