Упражнение
2
Выручка монополии при цене 10 ден.
ед. равна 40 ден. ед., а при цене 15 - 30 ден. ед. Найдите выручку при цене 2 ден.
ед., если функция спроса линейна.
Определите, при каком выпуске выручка максимальна.
При каких ценах увеличение выпуска ведет к сокращению выручки?
Решение:
Найдем уравнение кривой спроса: проходящей через
две точки.
В
(10, 4) и С(15,2).
Направляющий вектор ВС = {10-15; 4-2} = {-5 ; 2}
Уравнение будет иметь вид: 2 (P-10) +5 (Q – 4) = 0.
2P
+ 5Q – 40 = 0
Найдем объем продукции при цене 2 ден. ед.
2*2 + 5 Q – 40 = 0
Q
= 36/5 = 7,2
Тогда выручка
= 7,2 * 2 = 14,4 ден. ед.
Найдем выручку
Q
= 5, тогда Р = 7,5, а выручка (В) = 37,5
Q
= 6, тогда Р = 5, а выручка (В) = 30
Q
= 7, тогда Р = 2,5, а выручка (В) = 12,5
Видим, что максимальная выручка достигается при
выпуске 4 ед. по цене 10 д. ед.
При ценах выше Р = 10 д. ед. увеличение выпуска
ведет к сокращению выручки.
Упражнение 4
Монополия может продавать продукцию на двух сегментах рынка
с различной эластичностью спроса: Q1 D = 160 - P1;
Q2 D = 160 - P2 .Ее функция
затрат имеет вид:
ТС = 5 + 5 Q
+ 0,25 Q2,
1) при каких ценах на каждом из сегментов монополия получит
максимальную прибыль?
2) как изменился бы объем продаж на каждом из сегментов и
прибыль монополии, если бы ценовая дискриминация была запрещена?
3) представьте результат решения графически.
Решение:
Первый сегмент
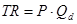, следовательно
Р1 = 160 – Q1
D
.
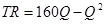Прибыль максимальна,
если MR = MC
MR = ТR| = 160 – 2 Q
МС = ТС| = 0,5 Q + 5.
Отсюда следует, что Q = 62 и Р = 98.
Прибыль = TR – TC = 98∙62 – 62 * 62 – 5 – 5 * 62
–0,25*622 = 956 д. ед.
По цене 98 д. ед.
Второй сегмент
Р2= (160 – Q2 D)
/ 2
.
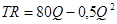MR = ТR| = 80 – Q
МС = ТС| = 0,5 Q + 5.
Отсюда следует, что Q = 50и Р = 55.
Прибыль = TR - TC = 80∙50 – 0,5*2500 –5 - 5*50
–0,25*502 = 1875 д. ед.
По цене 55 д. ед.
Если монополист не проводит дискриминации, то он продает
оптимальный объем Q* по единой цене Р*. Дополнительная прибыль от реализации
каждой дополнительной единицы от 0 до Q* (или предельная прибыль, МП) равняется
разнице между предельным доходом и предельными издержками.
МП=MR-MC
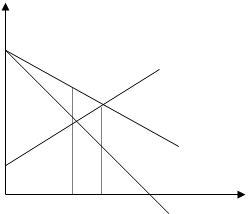
Совокупная прибыль (ТП) фирмы соответствует заштрихованной
площади АBС. В этих условиях производство любого количества сверх оптимального
сократит экономическую прибыль монополиста и потому невыгодно.
MC, MR
А
P* М МС
В
D
Q* MR Q
Если монополист проводит ценовую дискриминацию, то единой
цены нет, все товары продаются по их ценам спроса, и каждая дополнительно
реализованная единица товара увеличивает совокупный доход на величину той цены,
по которой она продается, т.е.
MR (Q) = P (Q).
Это означает, что кривая предельного дохода становится
тождественна кривой спроса, как в модели совершенной конкуренции. Однако в
отличие от конкурентного рынка, при котором существует единая рыночная цена,
для монополии, осуществляющей ценовую дискриминацию, цены разных единиц
продукции различны.
Оптимальный объем производства монополиста, осуществляющего
совершенную ценовую дискриминацию, расширяется до точки оптимума Q** совершенно
конкурентного рынка, а совокупная прибыль монополиста увеличивается (площадь
треугольника АКС).
MC, MR
А
М МС
К
В
D
Q* Q**
MR Q
Упражнение
5
Функция спроса на монополизированном рынке имеет вид: QD= 301 - Р, функция общих затрат монополии – ТС =
120+Q+Q2, капиталоемкость
производства характеризуется формулой К = 500Q.
По какой цене будет продаваться продукция при стремлении
монополии к максимуму:
I) прибыли;
2) выручки; 3) нормы прибыли.
Решение:
1) 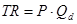, следовательно
Р = 301 - QD
.
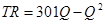Прибыль максимальна,
если MR=MC
MR = ТR| = 301 – 2Q
МС = ТС| = 2Q + 1.
Отсюда следует, что Q=75 и Р=226.
Прибыль = TR-TC=226∙75 – 120-75 - 752
= 11130 д. ед.
По цене 226 д. ед.
2) Найдем точку
максимума кривой выручки .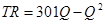
Q0
= -301 / (-2) = 150,5
Тогда Р =
301 – Q = 301
– 150,5 = 150,5 д. ед.
3) Р = (226 + 150,5) / 2 = 188,25 д. ед.