Задача. Построить модель связи между указанными факторами, проверить ее адекватность, осуществить точеный и интервальный прогноз.

Стоимость основных производственных фондов (X, млн.руб.)

2,3

2,5

2,0

2,9

3,3

5,0

3,8

4,0

7,4

7,5

Среднесуточная производительность (Y, тонн)

22,0

24,7

22,4

25,1

27,0

29,4

34,2

30,6

35,2

33,9

Решение:

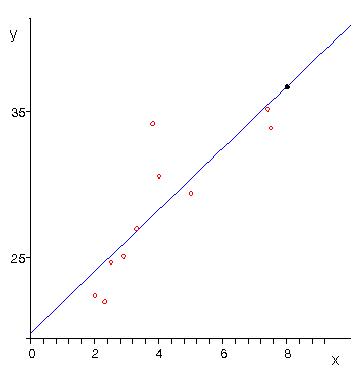
1)    По исходным данным нанесем на координатную плоскость точки

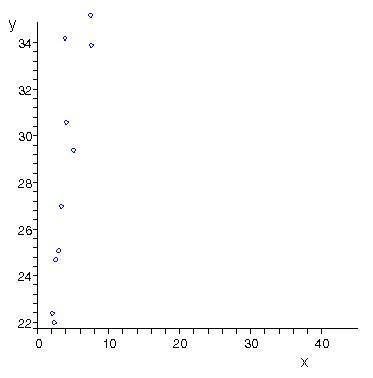
 Вид рассеивания точек позволяют выдвинуть гипотезу о том, что зависимость среднесуточной производительностью  (y) от стоимости основных производственных фондов () описывается линейной моделью вида:

где a и b - неизвестные постоянные коэффициенты.

2) Парный коэффициент корреляции будем искать по формуле:

Все расчеты запишем в таблицу

	X	Y	X2	Y2	XY
	2,3	22	5.29	484	50.6
	2,5	24.7	6.25	610.09	61.75
	2	22.4	4	501.76	44.8
	2,9	25.1	8.41	630.01	72.79
	3,3	27	10.89	729	89.1
	5	29.4	25	864.36	147
	3,8	34.2	14.44	1169.64	129.96
	4	30.6	16	936.36	122.4
	7,4	35.2	54.76	1239.04	260.48
	7,5	33.9	56.25	1149.21	254.25
Сумма	40,7	284.5	201.29	8313.47	1233.13

Тогда

Для оценки значимости r применяется t-критерий Стьюдента. При этом определяется фактическое значение критерия t_r:

По таблице критических точек распределения Стьюдента, по заданному уровню значимости α=0,05 и числу степеней свободы k=n-2 , находим критическую точку t_к=2,23. Так как t_r> t_к , то величина коэффициента корреляции признается существенной. Следовательно, X и Y коррелированны и связь между ними средняя.

3) Оценка параметров уравнений регрессии осуществляется методом наименьших квадратов. Сущность метода наименьших квадратов заключается в нахождении параметров модели a и b, при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических. Для выражения прямолинейной формы зависимости между X и Y применяется формула:

Для расчета параметров a и b линейной регрессии решаем систему уравнений:

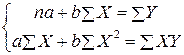
Для определения параметров уравнения на основе требований метода наименьших квадратов составляется система нормальных уравнений:

              

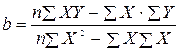
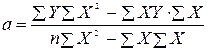
Найдем коэффициенты a и b:

Таким образом, уравнение линии регрессии имеет вид:

4) Наглядное изображение анализируемых данных, то есть применение графического метода (путем построения корреляционного поля точек эмпирической линии регрессии), не дает обобщенную количественную оценку адекватности того или иного уравнения связи. Более продуктивно использование критерия минимальной остаточной дисперсии и показателя средней ошибки аппроксимации :

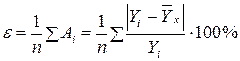
где  - теоретические значения.

Подставляя в уравнение регрессии фактические значения X, определим теоретические значения . Все расчеты запишем в таблицу:

		Ai
27.713	-2.713	12,3
25.135	-0.435	1,8
24.08	-1.68	7,5
25.975	-0.879	3,5
26.823	0.177	0,7
30.41	-1.01	3,4
27.878	6.322	18,5
28.3	2.3	7,5
35.474	-0.274	0,8
35.685	-1.785	5,3
Сумма	61,3

Найдем среднюю ошибку аппроксимации:

В среднем расчетные значения отклоняются от фактических на 6.13%.

5) Проверим значимость коэффициентов a и b по t-критерию Стьюдента.

Выдвигаем гипотезу H₀ о статистически незначимом отличии показателей от нуля: a= b=0.

t_табл. для числа степеней свободы k=n-2=10-2=8 и α=0.05 составит 2.23

Определим случайные ошибки m_a, m_b:

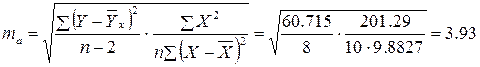
Тогда

;  

Фактические значения t-статистики превосходят табличные значения:

поэтому гипотеза H₀ отклоняется, т.е. a и  b не случайно отличаются от нуля, а статистически значимы.

Рассчитаем доверительный интервал для a и  b:

            

             

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью p= 1 - α =0.95 параметры . a и  b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.

6) Проверим адекватность модели

Рассчитаем F-критерий:

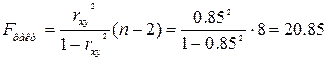
=5.32

Так как  >, то признается статистическая значимость и надежность уравнения регрессии.

7)

Вариация результата Y	Число степеней свободы	Сумма квадратов отклонений	Дисперсия на одну степень свободы		α=0,05 k1=1, k2=8
Общая	n-1=9	273.5	-	-	-
Факторная	k1=m=1	197.61	197.61	20.85	5.32
Остаточная	k2=n-m-1=8	75.89		-	-

8) В качестве прогнозной точки возьмем , тогда прогнозное значение

9) Ошибка прогноза составит:

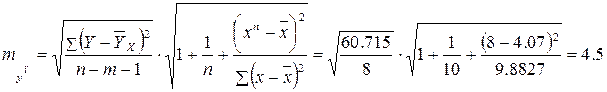
Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:

Доверительный интервал прогноза:

36,74±10,04

 

                                                                                                     (xⁿ,yⁿ)