Содержание

Задача №1 (3). 3

Задача №2(13) 8

Задача №3(23) 9

Задача №4(33) 11

Задача №5(43) 13

Задача №6(53) 14

Список используемой литературы.. 17

 

Задача №1 (3).

По приведенным данным табл.2 построить интервальный ряд распределения.

Для получения интервального ряда вычислить:

1. Среднюю арифметическую по качественному признаку для всей совокупности

2. Среднюю арифметическую для каждой группы

3. Моды, медиану

4. Общую дисперсию

5. Среднее квадратичное отклонение

6.     Коэффициент вариации

7.     Дисперсию по каждой группе

8.     Среднюю из групповых дисперсий

9.     Межгрупповую дисперсию

Номер рабочего	Выработка, тыс.руб
1	7,5
2	7,0
3	8,4
4	12,0
5	9,5
6	8,0
7	8,5
8	4,5
9	4,4
10	12,4
11	8,1
12	7,0
13	6,5
14	6,1
15	8,7
16	6,4
17	7,9
18	11,8
19	10,3
20	9,0

Сделать выводы.

Решение:

Номер рабочего	Выработка, тыс.руб	Сумма накопленных частот
1	7,5	7,5
2	7,0	14,5
3	8,4	22,9
4	12,0	34,9
5	9,5	44,4
6	8,0	52,4
7	8,5	60,9
8	4,5	65,4
9	4,4	69,8
10	12,4	82,2
11	8,1	90,3
12	7,0	97,3
13	6,5	103,8
14	6,1	109,9
15	8,7	118,9
16	6,4	125
17	7,9	132,9
18	11,8	144,7
19	10,3	155
20	9,0	164

1. Найдем среднюю арифметическую по формуле:

3. Значение моды определяется по формуле:

Медиана вычисляется по формуле:

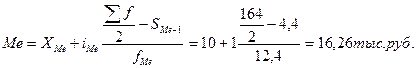
         4. Общая дисперсия находится по формуле:

5. Тогда среднее квадратичное отклонение будет равно:

тыс.руб.

  т. е. отклонение от средней выработки работников у 20 опрошенных составляет 2,16 тыс. руб.

6.         Коэффициент вариации равен:

т.е. отклонение от средней выработки работников у 20 опрошенных 26,34%

Сделает группировку по выработки работников.

№ группы	Группы выработки, тыс.руб.	№ рабочего	Выработка, тыс.руб.
1	4,4 – 8,4	1	7,5
		2	7,0
		6	8,0
		8	4,5
		9	4,4
		11	8,1
		12	7,0
		13	6,5
		14	6,1
		16	6,4
		17	7,9
	Итого по группе	11	73,4
2	8,4 – 12,4	3	8,4
		4	12,0
		5	9,5
		7	8,5
		10	12,4
		15	8,7
		18	11,8
		19	10,3
		20	9,0
	Итого по группе	9	90,6

2. Найдем среднюю арифметическую для каждой группы

7. Найдем дисперсию для каждой группы по формуле:

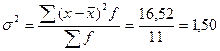
8. Средняя из групповых дисперсий равна:

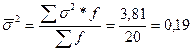
10.           Межгрупповая дисперсия:

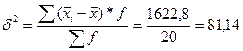
Задача №2(13)

Используя приведенные ниже данные по предприятиям объединения, вычислить средний процент выполнения плана по объединению в целом (табл.5).

завод	Фактический выпуск продукции, тыс.руб.	Процент выполнения плана, %
1	100	102
2	500	180
3	300	100

Проверить правильность расчета.

Решение:

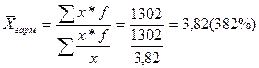
Проверка: =  = 382%=382%

Задача №3(23)

Проведено 10 – процентное выборочное бесповторное обследование. Необходимо по исходным данным табл.13 определить:

1.     средний качественный признак

2.     дисперсию и среднее квадратическое отклонение

3.     коэффициент вариации

4.     границы, в которых изменяется средняя качественного признака с вероятностью 0,954

5.     границы, в которых изменяется доля самых крупных единиц совокупности с вероятностью 0,997

 Сделать выводы.

Решение:

Стаж, лет	Количество рабочих	Среднее значение
До 5	12	2,5	30	1212,03
5-10	25	7,5	187,5	637,56
10-15	30	12,5	375	0,075
15-20	20	17,5	350	490,05
20-25	9	22,5	202,5	891,02
Более 25	4	27,5	110	894,01
Итого	100		1255	4124,75

1.

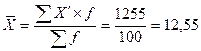
2.

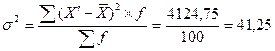
3.

4.

N=

x₁= 12,55-1.22=11,33

x₂= 12,55+1,22=13,77

11,33

Таким образом с вероятностью 0,954 средняя качественного признака изменяется в пределах от 11,33 до 13,77

5.

P=

P₁=75%-12,32%=62,68%

P₂=75%+12,32%=87,32%

62,68%

доля самых крупных единиц совокупности изменяется в пределах от 62,68% до 87,32%.

Задача №4(33)

 По исходным данным табл.14 определить:

1.     вид ряда динамики

2.     за каждый год:

-         абсолютный прирост

-         темп роста

-         темп прироста

-         абсолютное значение 1%-го прироста

3.     за весь период

-         средний уровень ряда динамики

-         средний темп роста

-         средний темп прироста

-         средний абсолютный прирост

Сделать выводы.

Решение:

год	Средняя годовая стоимость основных фондов, млн.руб.	Абсолютный прирост	Темп роста, %	Темп прироста, %	Абсолютное значение 1%-го прироста
цепной	базисный	цепной	базисный	цепной	базисный
2001	15,2	-	-	-	100	-	-	-
2002	16,7	1,5	1,5	109,87	109,87	9,87	9,87	0,1520
2003	24,3	7,6	9,1	145,51	159,87	45,51	57,87	0,1670
2004	20,5	-3,8	5,3	84,36	134,87	-15,64	34,87	0,2430
2005	22,7	2,2	7,5	110,73	149,34	10,73	49,34	0,2050

1.     Интервальный ряд динамики

2.     Расчет произведен в таблице.

3.

Вывод: за весь период с 2001 по 2005 года средняя годовая стоимость основных фондов увеличилась на 10,55%.

Задача №5(43)

По исходным данным табл.15 определить:

1.                              общие индексы затрат на производство продукции, физического объема продукции, себестоимости продукции.

2.                              абсолютное изменение затрат на производство продукции

3.                              влияние факторов на изменение затрат на производство продукции

Решение:

Вид продукции или предприятие, выпускающее однородную продукцию	Базисный период	Отчетный период	Изменение объема выпуска в отчет. периоде по сравнению с баз., %	Изменение себестоимости в отчет. периоде по сравнению с баз., %
Себестоимость единицы продукции, руб.	Выпуск, шт.	Затраты на выпуск, тыс.руб.	Себестоимость единицы продукции, руб.	Выпуск, шт.	Затраты на выпуск, тыс.руб.
А	-	-	500	-	-	550	-	-5
В	-	-	1000	-	-	1200	-	-2

J_{вып. А}=

J_{вып. В}=

2.

 

Задача №6(53)

По исходным данным определить:

1.                           уравнение регрессии, характеризующее зависимость результативного признака от факторного

2.                           линейный коэффициент корреляции

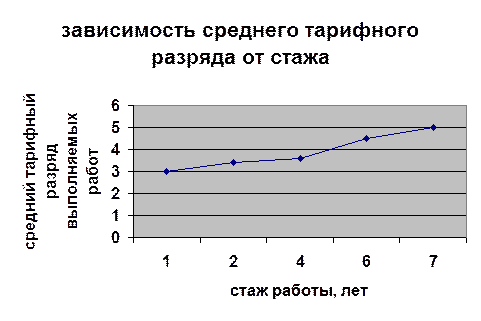
Дайте экономическую интерпретацию полученных результатов. Постройте график зависимости с изображением фактических данных.

Показатели	Номер предприятия (рабочего)
1	2	3	4	5
Стаж работы, лет	1	4	6	2	7
Средний тарифный разряд выполняемый работ	3,0	3,6	4,5	3,4	5

Решение:

№	Стаж работы, (х)	Средний тарифный разряд выполняемых работ, (у)	Х2	У2	ХУ
1	1	3,0	1	9	3	2,94
2	4	3,6	16	12,96	14,4	3,9
3	6	4,5	36	20,25	27	4,54
4	2	3,4	4	11,56	6,8	3,26
5	7	5	49	25	35	4,86
итого	20	19,5	106	78,77	86,2	19,5

1.     Уравнение линейной регрессии:

Система нормальных уравнений для данного примера имеет вид:

Подставим в эту систему найденные в таблице значения и получим

5а₀+20а₁=19,5

20а₀+106а₁=86,2

Решив данную систему, у нас получится а₁ = 0,32

Подставим полученное значение а₁ в первое уравнение и выразим а_0,  тогда получим: а₀ = 3,9-4*0,32=2,62

Линейное уравнение корреляционной связи будет иметь следующий вид:

У_х = 2,62+0,32 Х

2.     Линейный коэффициент корреляции исчисляется по формуле:

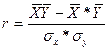
Из  полученных данных можно сделать вывод, т.к. коэффициент корреляции равен 0,005, то характер связи – прямой, а это значит, что с увеличением значения Х увеличивается значение У.

                      

Список используемой литературы

1.     Елисеева И.И., Юздашев М.М. Общая теория статистики. – М.: Финансы и статистика,1996.

2.     Статистика \ Под ред. проф. И.И. Елисеевой. – М.: ООО «ВИТ-РЕМ»,2002.

3.     Статистика\ Под ред.В.Г.Ионина. – Новосибирск: Издательсьво НГАЭиУ, М.: ИНФРА-М, 1997.

4.     Статистика \ И.Е. Теслюк, В.А. Тарловская, И.Н. Терлиженко и др. – Мн.:Ураджай, 2000г.

5.     Теория статистики \ Под ред. Р. А. Шмойловой.- М.: Финансы и статистика,2002.