Введение
Коммерческое производство начинается с закупки зданий, сооружений,
оборудования, производственных запасов, что требует инвестиционных вложений.
Инвестиционная деятельность является весьма рискованным видом финансовой
деятельности. Наибольшей ответственности требуют долгосрочные инвестиционные
вложения, которые не сразу приносят отдачу. По данным западноевропейской и
американской статистики, работа вновь образованных предприятий или нового
проекта в среднем в течение 2-3 лет является убыточной. Ясно, что для
существования в первоначальный убыточный период необходимы либо кредит, либо
накопленные или привлечённые под проект средства. После этого начатое дело или
проект начинают приносить прибыль. Поэтому в бизнесе необходима достаточная
целеустремлённость, чтобы не отказаться от своей программы, не разменять проект
на побочные мелкие, но дающие более быструю отдачу занятия. Если это удаётся,
фирма имеет шанс расти, укрепиться.
Для обеспечения долговременной финансовой стабильности и устойчивости
организаций их руководство нуждается в стратегическом подходе при решении
долгосрочных финансовых задач, в способах повышения их эффективности,
минимизации риска инвестиционных проектов.
Главной целью разрабатываемых стратегий является выработка эффективных
способов инвестирования, инструментов управления инвестициями на основе методов
и моделей инвестиционного анализа и прогнозирования. Используемые модели
призваны обеспечить оптимизацию решений в стратегических аспектах управления
инвестициями и связанных с ними риском.
В рамках данной работы поставлена цель изучения простого и сложного
процентов.
План
Теоретическая
часть. 4
Задание 1: Простой и сложный процент: понятие, методика,
пример вычисления 4
1. Процентная ставка: общее понятие. 4
2. Простой процент: понятие и методика исчисления. 5
3. Сложный процент: понятие и методика исчисления. 11
Практическая часть. 17
Задание 2. 17
Задание 3. 19
Список литературы.. 20
Теоретическая часть
Задание 1: Простой и сложный
процент: понятие, методика, пример вычисления
1. Процентная ставка: общее понятие
|
Давая деньги в долг, кредитор упускает возможность использовать их до
момента возврата. Заемщик должен выплатить компенсацию за ожидание кредитора.
Компенсация обычно выражается в форме процента.
Процентом
называют доход в денежной форме, выплачиваемый кредитору за пользование его
деньгами. Процент начисляется на основную сумму вклада (займа) по определенной
процентной ставке с определенной периодичностью, например, ежегодно[2, с. 145].
Пример 1
Рассмотрим вложение 1000 рублей на счет в банке сроком 3 года при ставке
10% годовых. Если по прошествии каждого года владелец снимает выплачиваемый
доход по вкладу 10%, результаты инвестирования будут таковы.
Таблица 1
Пример расчета процента
|
Основная
сумма вклада
|
Доход
за год при процентной ставке 10% годовых
|
На
конец года на счете
|
Снято
со счета по прошествии года
|
Остаток
на счете
|
|
1 год 1000
|
1000/100х10=100
|
1100
|
100
|
1000
|
|
2 год 1000
|
1000/100х10=100
|
1100
|
100
|
1000
|
|
3 год 1000
|
1000/100х10=100
|
1100
|
100
|
1000
|
За 3 года инвестор получил 100 рублей по окончании первого года, 100
рублей по окончании второго года и 100 рублей по окончании третьего года, что
совпало с окончанием срока вклада. В результате инвестирования в течение 3 лет
получено 300 рублей сверх основной суммы вклада 1000 рублей. Всего 1300 рублей.
2. Простой процент: понятие и методика исчисления
Если инвестированный капитал ежегодно увеличивается на величину произведения
исходного инвестированного капитала PV на требуемую норму доходности r (PV * r), инвестиция
осуществлена на условиях простого процента. В этом случае размер
инвестированного капитала через n лет будет равен:
FVпрn = PV + PV* r + ...+PV* r = PV*(1 + n * r), (1)
Таким образом, простой процент начисляется исходя из ставки процента и
исходной суммы вне зависимости от накопленного дохода. Такая схема соответствует
случаю, когда доход от вклада периодически выплачивается заемщиком и тут же
изымается кредитором[3, с. 58].
Пример 2
Рассмотрим вложение 1000 рублей на банковский депозит сроком 3 года при
ставке 10% годовых при условии, что владелец НЕ снимает в конце каждого года
полученные в качестве дохода 10%, но оставляет их на счете с целью реинвестирования
по той же процентной ставке (10%).
Таблица 2
Пример расчета простого процента
|
Основная сумма
вклада, начало года
|
Доход за год,
годовых
|
Снято со счета по
прошествии года
|
Остаток на счете на
конец года
|
|
1 год 1000
|
1000х10%=100
|
0
|
1000 + (1000x10%) =
1000x(1 + 0.1) = 1100
|
|
2 год 1100
|
1100х10%=110
|
0
|
1100 + (1100x10%) =
1100x(1 + 0.1) = 1210
|
|
3 год 1210
|
1210х10%=121
|
0
|
1210 + (1210x10%) =
1210x(1 + 0.1) = 1330
|
По окончании трех лет инвестор получит кроме основной суммы вклада 1000
рублей 331 рубль. Всего 1331 рубль.
Таким образом, если сравнивать условия без инвестирования процента (простой
процент) и с учетом инвестирования процента (сложный процент), то результаты
инвестирования по второй схеме превосходят результаты инвестирования по первой
схеме на 31 рубль. Это произошло по причине реинвестирования процента.
В случае использования простых процентов в банковской практике по
краткосрочным ссудам со сроком погашения до одного года в качестве показателя n берётся величина, характеризующая удельный вес длины
внутригодовых периодов (день, месяц, квартал, полугодие) в общем периоде (год).
Продолжительность временных интервалов может округляться до месяца - 30 дней,
квартала - 90 дней, полугодия - 180 дней, года - 360 или 365 дней[1, 8 и др.].
Пример 3
Выдана ссуда в размере 4 млн. руб. на один месяц под 10% годовых. Тогда
размер платежа к погашению по формуле (1) будет равен:
FVn = 4 [ 1 + (30 / 360) * (10 / 100)] = 4,03
млн. руб.
Рассмотрим процесс наращения (accumulation),
т.е. определения денежной суммы в будущем, исходя из заданной суммы сейчас.
Экономический смысл операции наращения состоит в определении величины той
суммы, которой будет или желает располагать инвестор по окончании этой
операции. Здесь идет движение денежного потока от на-стоящего к будущему.
Величина FV показывает будущую стоимость "сегодняшней"
величины PV при заданном уровне интенсивности начисления процентов i.
При использовании простых ставок процентов проценты (процентные деньги)
определяются исходя из первоначальной суммы долга. Схема простых процентов предполагает
неизменность базы, с которой происходит начисление процентов.
Из определения процентов не трудно заметить, что проценты (процентные
деньги) представляют собой, по сути, абсолютные приросты:
I = FV - PV, (2)
а поскольку база для их начисления является постоянной, то за ряд лет
общий абсолютный прирост составит их сумму или произведение абсолютных
приростов на количество лет ссуды:
I = (FV - PV) n = [(FV
- PV) / PV • PV] n = i • PV • n,, (3)
где i = (FV - PV) / PV
по определению процентной ставки.
Таким образом, размер ожидаемого дохода зависит от трех факторов: от величины
инвестированной суммы, от уровня процентной ставки и от срока финансовой
операции[7, с. 12].
Тогда наращенную сумму по схеме простых процентов можно будет определять
следующим образом:
FV = PV
+ I = PV + i • PV • n = PV (1 + i
• n) = PV • kн, (4)
где kн – коэффициент
(множитель) наращения простых процентов.
Данная формула называется "формулой простых процентов".
Поскольку коэффициент наращения представляет собой значение функции от
числа лет и уровня процентной ставки, то его значения легко табулируются. Таким
образом, для облегчения финансовых расчетов можно использовать финансовые
таблицы, содержащие коэффициенты наращения по простым процентам.
Пример 4. Сумма в размере 2'000 рублей дана в долг на 2
года по схеме простого процента под 10% годовых. Определить проценты и сумму,
подлежащую возврату.
Решение:
Наращенная сумма:
FV = PV (1 + n • i ) = 2'000 (1 + 2 • 0'1) = 2'400 руб.
или
FV = PV • kн = 2'000 • 1,2
= 2'400 руб.
Сумма начисленных процентов:
I = PV • n • i =
2'000 • 2 • 0,1 = 400 руб.
или
I = FV - PV = 2'400 - 2'000 = 400 руб.
Таким образом, через два года необходимо вернуть общую сумму в размере
2'400 рублей, из которой 2'000 рублей составляет долг, а 400 рублей – "цена
долга".
Следует заметить, что подобные задачи на практике встречаются редко,
поскольку к простым процентам прибегают в случаях:
- выдачи краткосрочных ссуд, т.е. ссуд, срок которых либо равен году,
либо меньше его, с однократным начислением процентов;
- когда проценты не присоединяются к сумме долга, а периодически выплачиваются.
В тех случаях, когда срок ссуды менее года, происходит модификация формулы:
а) если срок ссуды выражен в месяцах ( М ), то величина
n выражается в виде дроби:
n = М / 12, (5)
тогда все формулы можно представить в виде:
FV = PV (1 + М / 12 • i); (6)
I = PV •
М / 12 • i; (7)
kн = 1 + М
/ 12 • i. (8)
Пример 5. Изменим условия предыдущего примера, снизив
срок долга до 6 месяцев.
Решение:
Наращенная сумма:
FV = PV (1 + М / 12 • i)
= 2'000 (1 + 6/12 • 0'1) = 2'100 руб.
или
FV = PV • kн = 2'000 • 1,05
= 2'100 руб.
Сумма начисленных процентов:
I = PV • М / 12 • i = 2'000 •
6/12 • 0,1 = 100 руб.
или
I = FV - PV = 2'100 - 2'000 = 100 руб.
Таким образом, через полгода необходимо вернуть общую сумму в размере
2'100 рублей, из которой 2'000 рублей составляет долг, а проценты – 100 рублей.
б) если время выражено в днях (t),
то величина n выражается в виде следующей
дроби:
n = t / T, (9)
где t – число дней ссуды, т.е.
продолжительность срока, на который выдана ссуда;
T – расчетное число дней в году (временная база).
Отсюда модифицированные формулы имеют следующий вид:
FV = PV (1 + t / T • i ); (10)
I = PV •
t / T • i; (11)
kн = 1 + t / T • i. (12)
Здесь возможны следующие варианты расчета:
Временную базу ( T ) можно представить
по-разному:
условно состоящую из 360 дней. В этом случае речь идет об обыкновенном
(ordinary interest),
или коммерческом проценте;
взять действительное число дней в году (365 или 366 дней). В этом случае
получают точный процент (exact interest).
Число дней ссуды ( t
) также можно по-разному определять[6, с. 122]:
условно, исходя из того, что продолжительность любого целого месяца
составляет 30 дней, а оставшиеся дни от месяца считают точно, – в результате
получают так называемое приближенное число дней ссуды;
используя прямой счет или специальные таблицы порядковых номеров дней
года, рассчитывают фактическое число дней между датами, – в этом случае получают
точное число дней ссуды.
Таким образом, если время финансовой операции выражено в днях, то расчет
простых процентов может быть произведен одним из трех возможных способов:
Обыкновенные проценты с приближенным числом дней ссуды,
или, как часто называют, "германская практика расчета", когда
продолжительность года условно принимается за 360 дней, а целого месяца –
за 30 дней. Этот способ обычно используется в Германии, Дании, Швеции.
Обыкновенные проценты с точным числом дней ссуды, или
"французская практика расчета", когда продолжительность года условно
принимается за 360 дней, а продолжительность ссуды рассчитывается точно по календарю.
Этот способ имеет распространение во Франции, Бельгии, Испании, Швейцарии.
Точные проценты с точным числом дней ссуды, или
"английская практика расчета", когда продолжительность года и
продолжительность ссуды берутся точно по календарю. Этот способ применяется в
Португалии, Англии, США.
Чисто формально возможен и четвертый вариант: точные проценты с
приближенным числом дней ссуды, – но он лишен экономического смысла.
Вполне естественно, что в зависимости от использования конкретной
практики начисления простых процентов их сумма будет различаться по абсолютной
величине.
Для упрощения процедуры расчета точного числа дней финансовой операции
пользуются специальными таблицами порядковых номеров дней года, в которых все
дни в году последовательно пронумерованы. Точное количество дней получается
путем вычитания номера первого дня финансовой операции из номера последнего дня
финансовой операции.
Пример 6. Сумма 2 млн руб.
положена в банк 18 февраля не високосного года и востребована 25 декабря того
же года. Ставка банка составляет 35% годовых. Определить сумму начисленных
процентов при различной практике их начисления.
Решение:
Германская практика начисления простых процентов:
Временная база принимается за 360 дней, T = 360.
Количество дней ссуды:
t = 11 (февраль) + 30 (март) + 30
(апрель) + 30 (май) + 30 (июнь) +
+ 30 (июль) + 30 (август) + 30 (сентябрь) + 30 (октябрь) +
+ 30 (ноябрь) + 25 (декабрь) - 1 = 305 дней
Сумма начисленных процентов:
I = P • t / T • i
= 2'000'000 • 305/360 • 0,35 = 593'055,55 руб.
Как видно, результат финансовой операции во многом зависит от выбора
способа начисления простых процентов. Поскольку точное число дней в большинстве
случаев больше приближенного числа дней, то и проценты с точным числом дней
ссуды обычно получаются выше процентов с приближенным числом дней ссуды.
В практическом смысле эффект от выбора того или иного способа зависит от
значительности сумм, фигурирующих в финансовой операции.
3. Сложный процент: понятие и методика исчисления
Если очередной годовой доход исчисляется не с исходной величины инвестированного
капитала, а с общей суммы, включающей также ранее начисленные и не
востребованные инвестором проценты, то инвестиция произведена в условиях
сложного процента. Начисления по ставке сложного процента ещё называют «компаутингом». В данном случае размер инвестированного
капитала будет равен[4,
с. 39]:
к концу первого года:
FV1 = PV + PV*r = PV*(1
+ r);
к концу второго года
FV2 = FV1 + FV1*r = FV1
(1+r) = PV*(1+r)2;
к концу n-го года:
FVn = PV(1+r)n, (13)
То, что инвестиция в условиях сложного процента гораздо выгоднее, чем в условиях
простого, подтверждает неравенство:
(1 + r)n
> 1 + n * r, (14)
т.е.
FVn > FVпрn при n > 1.
В случае применения сложного процента капитал, генерирующий доходы,
постоянно возрастает, что повышает заинтересованность вкладчика в оставлении
инвестированного и полученного в результате инвестирования капитала в том же
объекте вложений. При применении простого процента вкладчик заинтересован
снимать доходы по мере их начисления для потребления или использования в других
инвестиционных проектах или в текущей деятельности.
Выражение (1+ r)n
называют процентным множителем (факторным множителем) или компаунтинговым
фактором, где r измеряется в долях единицы. Факторный
множитель показывает, чему будет равна денежная единица (рубль, доллар, марка, йена и др.) через n периодов при
заданной процентной ставке r. Для удобства расчётов
существуют таблицы, в которых значения факторного множителя табулированы
(представлены их расчётные значения) для различных значений r
и n.
Сложный процент начисляется исходя из ставки процента и суммы, накопленной
на счете к началу очередного периода с учетом накопленного дохода. Такая схема
соответствует случаю, когда доход от вклада периодически выплачивается
заемщиком, но не изымается кредитором, а остается у заемщика, увеличивая сумму
займа[10, с. 172].
Естественно, эта схема подвергает кредитора большему риску, соответственно
он получает и большее вознаграждение.
В финансовой практике значительная часть расчетов ведется с использованием
схемы сложных процентов.
Применение схемы сложных процентов целесообразно в тех случаях, когда:
- проценты не выплачиваются по мере их начисления, а присоединяются к
первоначальной сумме долга. Присоединение начисленных процентов к сумме долга,
которая служит базой для их начисления, называется капитализацией
процентов;
- срок ссуды более года.
Если процентные деньги не выплачиваются сразу по мере их начисления, а
присоединяются к первоначальной сумме долга, то долг, таким образом, увеличивается
на невыплаченную сумму процентов, и последующее начисление процентов происходит
на увеличенную сумму долга:
FV = PV
+ I = PV + PV • i = PV • (1 + i), (15)
– за один период начисления;
FV = (PV + I) • (1 + i) = PV • (1 + i)
• (1 + i) = PV • (1 + i)2, (16)
– за два периода начисления;
отсюда, за n периодов начисления
формула примет вид:
FV = PV • (1 + i)n
= PV • kн , (17)
где FV – наращенная сумма долга;
PV – первоначальная сумма долга;
i – ставка процентов в периоде
начисления;
n – количество периодов начисления;
kн – коэффициент
(множитель) наращения сложных процентов.
Эта формула называется формулой сложных процентов.
Как было выше указано, различие начисления простых и сложных процентов в
базе их начисления. Если простые проценты начисляются все время на одну и ту же
первоначальную сумму долга, т.е. база начисления является постоянной величиной,
то сложные проценты начисляются на увеличивающуюся с каждым периодом начисления
базу. Таким образом, простые проценты по своей сути являются абсолютными
приростами, а формула простых процентов аналогична формуле определения уровня
развития изучаемого явления с постоянными абсолютными приростами. Сложные
проценты характеризуют процесс роста первоначальной суммы со стабильными
темпами роста, при наращении ее по абсолютной величине с ускорением,
следовательно, формулу сложных процентов можно рассматривать как определение
уровня на базе стабильных темпов роста[3, 11 и др.].
Согласно общей теории статистики, для получения базисного темпа роста
необходимо перемножить цепные темпы роста. Поскольку ставка процента за период
является цепным темпом прироста, то цепной темп роста равен:
(1 + i), (18)
Тогда базисный темп роста за весь период, исходя из постоянного темпа прироста,
имеет вид:
(1 + i)n
, (19)
Базисные темпы роста или коэффициенты (множители) наращения, зависящие от
процентной ставки и числа периодов наращения, табулированы. Экономический смысл
множителя наращения состоит в том, что он показывает, чему будет равна одна
денежная единица (один рубль, один доллар и т.п.) через n
периодов при заданной процентной ставке i.
При краткосрочных ссудах начисление по простым процентам предпочтительнее,
чем по сложным процентам; при сроке в один год разница отсутствует, но при
среднесрочных и долгосрочных ссудах наращенная сумма, рассчитанная по сложным
процентам значительно выше, чем по простым.
При любом i,
если 0 < n < 1, то (1 + ni) > (1 + i)n ;
если n > 1, то (1 + ni) < (1 + i)n ;
если n = 1, то (1 + ni) = (1 + i)n .
Таким образом, для лиц, предоставляющих кредит:
- более выгодна схема простых процентов, если срок ссуды менее года
(проценты начисляются однократно в конце года);
- более выгодной является схема сложных процентов, если срок ссуды превышает
один год;
- обе схемы дают одинаковый результат при продолжительности периода один
год и однократном начислении процентов.
Пример. Сумма в размере 2'000 долларов дана в долг на 2
года по ставке процента равной 10% годовых. Определить проценты и сумму,
подлежащую возврату.
Решение:
Наращенная сумма
FV = PV • (1 + i)n = 2'000 • (1 + 0'1)2 =
2'420 долларов
или
FV = PV • kн = 2'000 • 1,21
= 2'420 долларов,
где kн = 1,21
Сумма начисленных процентов
I = FV - PV = 2'420 - 2'000 = 420 долларов.
Таким образом, через два года необходимо вернуть общую сумму в размере
2'420 долларов, из которой 2'000 долларов составляет долг, а 420 долларов –
"цена долга".
Достаточно часто финансовые контракты заключаются на период, отличающийся
от целого числа лет[9, с. 148].
В случае, когда срок финансовой операции выражен дробным числом лет,
начисление процентов возможно с использованием двух методов:
общий метод заключается в прямом расчете по формуле сложных
процентов:
FV = PV • (1 + i)n, (20)
n = a + b, (21)
где n – период сделки;
a – целое число лет;
b – дробная часть года.
смешанный метод расчета предполагает для целого числа лет
периода начисления процентов использовать формулу сложных процентов, а для дробной
части года – формулу простых процентов:
FV = PV • (1 + i)a • (1 + bi), (22)
Поскольку b < 1, то (1 + bi) > (1 + i)a, следовательно, наращенная сумма
будет больше при использовании смешанной схемы.
Пример. В банке получен кредит под 9,5% годовых в
размере 250 тыс. долларов со сроком погашения через два года и 9 месяцев.
Определить сумму, которую необходимо вернуть по истечении срока займа двумя
способами, учитывая, что банк использует германскую практику начисления процентов.
Решение:
Общий метод:
FV = PV • (1 + i)n = 250 • (1 + 0,095)2,9 =
320,87 тыс. долларов.
Смешанный метод:
FV = PV • (1 + i)a • (1 + bi)
=
= 250 • (1 + 0,095)2 • (1 + 270/360 • 0,095) =
= 321,11 тыс. долларов.
Таким образом, по общему методу проценты по кредиту составят
I = S - P = 320,87 - 250,00 = 70,84 тыс. долларов,
а по смешанному методу
I = S - P = 321,11 - 250,00 = 71,11 тыс. долларов.
Как видно, смешанная схема более выгодна кредитору.
Практическая часть
Задание 2
УСЛОВИЕ ЗАДАНИЯ
На предприятии разработаны два варианта освоения инвестиций в объеме 50 млн. у.е. Сметная стоимость
создаваемого объекта и срок освоения инвестиций одинаковы, но структура
затрат по годам освоения инвестиций различна. Требуемая норма прибыли – 54 %.
Расчетным годом считать первый год периода.
Проведите экономическое
обоснование выбора более предпочтительного
варианта инвестирования.
РЕШЕНИЕ
Имеем следующие исходные данные по вариантам строительства объектов
Таблица 3
Исходные данные задания
|
Вариант
|
Годы
|
Сумма
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
6
|
7,5
|
10
|
12
|
14,5
|
50
|
|
2
|
14
|
12,5
|
11
|
7,5
|
5
|
50
|
Норма прибыли r = 54 %. Пусть
ставка дисконта Ен – 12 %.
1)
Индекс доходности представляет собой отношение суммы
приведенных эффектов к величине капиталовложений:
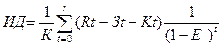, (23)
Rt
– результаты, достигнутые в t
– ом году
Зt – затраты,
осуществляемые в t – м году, тыс. руб.
Kt – капитальные вложения в t – м году, тыс.
руб.
Et –
норма дисконта, %
2)
Чистый дисконтированный доход равен:
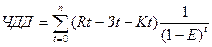, (24)
t – продолжительность
расчетного периода
Значение Rt определяем по формуле:
Rt
= Зt+Зt*r , (25)
ПО ПРОЕКТУ 1:
Таблица
4
Результаты
расчетов по проекту 1
|
Годы
|
Rt
|
Зt
|
Kt
|
(Rt-Зt-Kt)/(1-Е)t
|
|
1
|
9,24
|
6
|
50
|
-53,1
|
|
2
|
11,55
|
7,5
|
0
|
5,2
|
|
3
|
15,4
|
10
|
0
|
7,9
|
|
4
|
18,48
|
12
|
0
|
10,8
|
|
5
|
22,33
|
14,5
|
0
|
14,8
|
|
ИТОГО
|
|
|
|
-14,3
|
Тогда:
ЧДД = -14,3 ( млн.
руб.)
Если решение принимать на основании ЧДД, то проект можно считать неэффективным,
так как ЧДД<0.
ПО ПРОЕКТУ 2:
Таблица
5
Результаты
расчетов по проекту 2
|
Годы
|
Rt
|
Зt
|
Kt
|
(Rt-Зt-Kt)/(1-Е)t
|
|
1
|
21,56
|
14
|
50
|
-48,2
|
|
2
|
19,25
|
12,5
|
0
|
8,7
|
|
3
|
16,94
|
11
|
0
|
8,7
|
|
4
|
11,55
|
7,5
|
0
|
6,8
|
|
5
|
7,7
|
5
|
0
|
5,1
|
|
ИТОГО
|
|
|
|
-18,9
|
Тогда:
ЧДД = -18,9 ( млн.
. руб.)
В целом проект можно считать неэффективным,
так как ЧДД<0.
ЧДД по проекту 1 хоть и отрицателен, но
выше, чем по проекту 2. Поэтому в данном случае в качестве более предпочтительного выбираем проект 1.
Задание 3
УСЛОВИЕ ЗАДАНИЯ
Компания владеет фабрикой, оборудование которой требует модернизации.
Имеются два варианта:
1)
потратить 9341000 у.е.
сейчас и получить 9341500 у.е. через 4 года;
2)
потратить 9341000 у.е. сейчас и получить 9341050 у.е.
через 1 год.
Первоначальные затраты единовременны. Требуемая норма прибыли – 10 %.
Проведите расчеты, необходимые для экономического обоснования выбора
варианта инвестирования, сделайте вывод.
РЕШЕНИЕ
1)
Величина наращенной стоимости равна:
Sn
= S1 * (1+iс)n, (26)
Где S1 – первоначальная сумма вклада, у.е.
Sn – величина наращенной стоимости, у.е.
i c - процентная ставка, норма прибыли, %
Для варианта 1:
9341000*(1+0,1) 4=
13676158,1 (у.е.)
Для варианта 2:
9341000*(1+0,1) = 10275100 (у.е.)
2) определим
величину разниц между возможной наращенной
стоимостью и полученной величиной:
13676158,1 – 9341500
= 4334658,1 (у.е.)
10275100-9341050
= 934050 (у.е.)
3)
Альтернативные потери выше в варианте 1.
Поэтому второй вариант инвестирования более выгоден.
Список литературы
1)
Балабанов И.Т. Основы финансового менеджмента:
Учеб.пособие.-3-е изд.,перераб.,доп., - М.: Финансы и
статистика,2002.-528с.: ил.
2)
Буянов В.П. Управление рисками (рискология)
/ Буянов В.П.,Кирсанов К.А.,Михайлов
Л.А..-М.: Экзамен,2002.-384 с
3)
Быльцов С.И. Настольная книга
российского инвестора. – М.: Юнити- ДАНА, 2000 . –
567 с.
4)
Вайнштейн С.Ю. Инвестиционная направленность финансовой
политики // Инвестиции в России. – 1996 .- № 1- 2
5)
Вайнштейн С.Ю Основы управления в малом бизнесе: Учеб. пособ. – Новосибирск: НГАЭ иУ,
1994 .- 389 с..
6)
Изряднова О.
Правительственная инвестиционная политика // Инвестиции в России. – 1996 .- №
1- 2
7)
Молотков Ю. И. Менеджмент: Учебно-
методический комплекс для дистанционного обучения. – Новосибирск: СибАГС, 2003. – 219 с.
8)
Молотков Ю.И. Менеджмент: Учеб. пособ.
– Новосибирск: СибАГС, 2001. – 234 с.
9)
Направления и формы государственного регулирования
рыночной экономикой / Под ред.О.И. Боткина. - Ижевск: изд-во инс-та экон. И управления Удмуртского
гос.ун-та,2002.-394 с
10)
Савчук В.П.
Анализ и разработка инвестиционных проектов. – М.: Инфра- М, 1999. – 456 с.
11)
Управление риском: Риск. Устойчивое развитие.
Синергетика. - М.: Наука,2000.- 431 с