ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА
СТАТИСТИКИ
О
Т Ч Е Т
о результатах выполнения
компьютерной лабораторной работы №1
«Автоматизированный априорный анализ
статистической совокупности
в среде MS Excel»
Вариант № 37
Выполнила: ст. III курса гр.2
Стешина О.С.
Специальность ГМУ
№ ЛИЧНОГО ДЕЛА
05МГД48037
Проверила: Вдовина И.В.
Брянск,
2006 г.
1.
Постановка задачи
При
проведении статистического наблюдения за деятельностью предприятий корпорации
получены выборочные данные по 32-м предприятиям, выпускающим однородную
продукцию (выборка 10%-ная,
механическая), о среднегодовой стоимости основных производственных фондов
и о выпуске продукции за год.
В
проводимом статистическом исследовании обследованные предприятия выступают как
единицы выборочной совокупности, а показатели Среднегодовая стоимость основных производственных фондов и Выпуск продукции – как изучаемые
признаки единиц.
Таблица 1
Исходные данные
|
A
|
B
|
C
|
|
3
|
Номер
единицы наблюдения
|
Среднегодовая стоимость
основных производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
4
|
1
|
2096,00
|
2008,50
|
|
5
|
2
|
2466,50
|
2203,50
|
|
6
|
3
|
2544,50
|
2457,00
|
|
7
|
4
|
2681,00
|
2730,00
|
|
8
|
5
|
1745,00
|
1365,00
|
|
9
|
6
|
2817,50
|
2340,00
|
|
10
|
7
|
2895,50
|
3159,00
|
|
11
|
8
|
2174,00
|
2145,00
|
|
12
|
9
|
2661,50
|
2515,50
|
|
13
|
10
|
3071,00
|
3139,50
|
|
14
|
11
|
3363,50
|
3315,00
|
|
15
|
13
|
2564,00
|
2613,00
|
|
16
|
14
|
2817,50
|
2847,00
|
|
17
|
15
|
3227,00
|
3451,50
|
|
18
|
16
|
3695,00
|
3705,00
|
|
19
|
17
|
2759,00
|
2496,00
|
|
20
|
18
|
3051,50
|
2964,00
|
|
21
|
19
|
2427,50
|
1852,50
|
|
22
|
20
|
3090,50
|
2535,00
|
|
23
|
21
|
3441,50
|
3412,50
|
|
24
|
22
|
2369,00
|
1930,50
|
|
25
|
23
|
1881,50
|
1813,50
|
|
26
|
24
|
3149,00
|
2905,50
|
|
27
|
25
|
2817,50
|
2535,00
|
|
28
|
26
|
2622,50
|
2398,50
|
|
29
|
27
|
2037,50
|
1560,00
|
|
30
|
28
|
2739,50
|
2437,50
|
|
31
|
29
|
3168,50
|
2671,50
|
|
32
|
30
|
3012,50
|
2535,00
|
|
33
|
32
|
2213,00
|
2262,00
|
В
процессе исследования совокупности необходимо решить ряд статистических задач
для выборочной
и генеральной совокупностей.
Статистический анализ выборочной совокупности
1.
Выявить наличие среди исходных данных резко
выделяющихся значений признаков («выбросов» данных) с целью исключения из
выборки аномальных единиц наблюдения.
2.
Рассчитать обобщающие статистические показатели
совокупности по изучаемым признакам: среднюю арифметическую (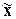 ), моду (Мо), медиану
(Ме), размах вариации (R), дисперсию(
), моду (Мо), медиану
(Ме), размах вариации (R), дисперсию(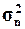 ), средние отклонения – линейное (
), средние отклонения – линейное (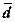 ) и квадратическое (σn),
коэффициент вариации (Vσ),
структурный коэффициент асимметрии
К.Пирсона (Asп).
) и квадратическое (σn),
коэффициент вариации (Vσ),
структурный коэффициент асимметрии
К.Пирсона (Asп).
3.
На основе рассчитанных показателей в предположении,
что распределения единиц по обоим признакам близки к нормальному, оценить:
а)
степень колеблемости значений признаков в совокупности;
б)
степень однородности совокупности по изучаемым признакам;
в)
устойчивость индивидуальных значений признаков;
г)
количество попаданий индивидуальных значений признаков в диапазоны (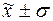 ), (
), (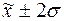 ), (
), (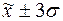 ).
).
4.
Дать сравнительную характеристику распределений единиц
совокупности по двум изучаемым признакам на основе анализа:
а)
вариации признаков;
б)
количественной однородности единиц;
в)
надежности (типичности) средних значений признаков;
г)
симметричности распределений в центральной части ряда.
5.
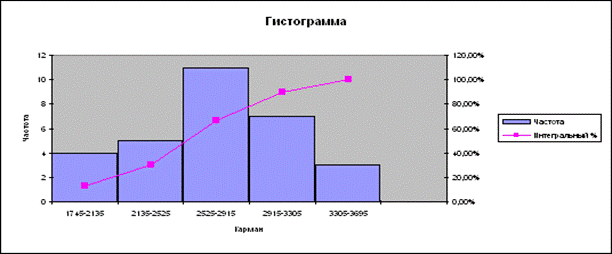
Построить интервальный вариационный ряд и гистограмму
распределения единиц совокупности по признаку Среднегодовая стоимость основных производственных фондов и
установить характер (тип) этого распределения. Рассчитать моду Мо полученного интервального ряда и
сравнить ее с показателем Мо
несгруппированного ряда данных.
Статистический анализ генеральной
совокупности
1.
Рассчитать генеральную дисперсию 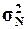 , генеральное
среднее квадратическое отклонение
, генеральное
среднее квадратическое отклонение 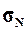 и
ожидаемый размах вариации признаков RN.
Сопоставить значения этих показателей для генеральной и выборочной дисперсий.
и
ожидаемый размах вариации признаков RN.
Сопоставить значения этих показателей для генеральной и выборочной дисперсий.
2.
Для изучаемых признаков рассчитать:
а)
среднюю ошибку выборки;
б) предельные ошибки выборки для уровней надежности P=0,683,
P=0,954, P=0,997 и границы, в которых будут находиться средние значения
признака генеральной совокупности при заданных уровнях надежности.
3.
Рассчитать коэффициенты асимметрии As и эксцесса Ek. На основе полученных оценок
сделать вывод о степени близости распределения единиц генеральной
совокупности к нормальному распределению.
2. Рабочий файл с результативными таблицами и графиками
|
|
|
|
|
|
Таблица
2
|
|
|
Аномальные
единицы наблюдения
|
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск
продукции, млн. руб.
|
|
|
12
|
1160,00
|
2925,00
|
|
|
31
|
3695,00
|
975,00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Описательные
статистики
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
Таблица
3
|
|
Столбец1
|
Столбец1
|
|
|
|
|
|
Среднее
|
2720
|
Среднее
|
2543,45
|
|
Стандартная
ошибка
|
86,11220627
|
Стандартная
ошибка
|
102,7244678
|
|
Медиана
|
2749,25
|
Медиана
|
2525,25
|
|
Мода
|
2817,5
|
Мода
|
2535
|
|
Стандартное
отклонение
|
471,6559785
|
Стандартное
отклонение
|
562,6450824
|
|
Дисперсия
выборки
|
222459,3621
|
Дисперсия
выборки
|
316569,4888
|
|
Эксцесс
|
-0,344943844
|
Эксцесс
|
-0,205332365
|
|
Асимметричность
|
-0,152503649
|
Асимметричность
|
0,042954448
|
|
Интервал
|
1950
|
Интервал
|
2340
|
|
Минимум
|
1745
|
Минимум
|
1365
|
|
Максимум
|
3695
|
Максимум
|
3705
|
|
Сумма
|
81600
|
Сумма
|
76303,5
|
|
Счет
|
30
|
Счет
|
30
|
|
Уровень
надежности(95,4%)
|
179,5277582
|
Уровень
надежности(95,4%)
|
214,1611999
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предельные
ошибки выборки
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
Таблица 4а
|
|
Столбец1
|
Столбец1
|
|
|
|
|
|
Уровень
надежности(68,3%)
|
87,67991917
|
Уровень
надежности(68,3%)
|
104,5946147
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предельные
ошибки выборки
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
Таблица 4б
|
|
Столбец1
|
Столбец1
|
|
|
|
|
|
Уровень
надежности(99,7%)
|
278,9520402
|
Уровень
надежности(99,7%)
|
332,7658311
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выборочные
показатели вариации и асимметрии
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
Таблица 5
|
|
Стандартное
отклонение
|
463,7284227
|
Стандартное
отклонение
|
553,188189
|
|
Дисперсия
|
215044,05
|
Дисперсия
|
306017,1725
|
|
Среднее
линейное отклонение
|
373,1
|
Среднее
линейное отклонение
|
426,14
|
|
Коэффициент
вариации, %
|
17,04883907
|
Коэффициент
вариации, %
|
21,74952089
|
|
Коэффициент
асимметрии
|
-0,21025237
|
Коэффициент
асимметрии
|
0,015275091
|
|
|
|
|
|
Таблица
6
|
|
|
|
Карман
|
Частота
|
|
|
|
|
|
|
|
1
|
|
|
|
2135
|
3
|
|
|
|
2525
|
5
|
|
|
|
2915
|
11
|
|
|
|
3305
|
7
|
|
|
|
3695
|
3
|
|
|
|
|
|
|
|
|
Таблица
7
|
|
|
Интервальный
ряд распределения предприятий по стоимости основных производственных фондов
|
|
Группы
предприятий по среднегодовой стоимости основных фондов
|
Число
предприятий в группе
|
Накопленная
частость группы,%
|
|
|
1745-2135
|
4
|
13,33%
|
|
|
2135-2525
|
5
|
30,00%
|
|
|
2525-2915
|
11
|
66,67%
|
|
|
2915-3305
|
7
|
90,00%
|
|
|
3305-3695
|
3
|
100,00%
|
|
|
|
|
|
|
|
Итого
|
30
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 3. Статистический
анализ выборочной совокупности
3. Статистический
анализ выборочной совокупности
1.
Количество аномальных единиц наблюдения – 2, согласно табл.2: предприятие № 31
со среднегодовой стоимостью производственных фондов - 3695 млн.руб., и выпуском
продукции – 945 млн.руб., и предприятие №12 со среднегодовой стоимостью
производственных фондов – 1160 млн.руб., и выпуском продукции – 2925 млн.руб.
2. Рассчитанные выборочные показатели
представлены в таблицах 3 5. Сформируем на основе этих таблиц единую таблицу
значений выборочных совокупностей:
|
|
|
Таблица
8
|
|
Описательные
статистики выборочной совокупности
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
|
|
|
|
Средняя арифметическая
|
2720
|
Средняя
арифметическая
|
2543,45
|
|
Медиана
|
2749,25
|
Медиана
|
2525,25
|
|
Мода
|
2817,5
|
Мода
|
2535
|
|
Размах
вариации
|
1950
|
Размах
вариации
|
2340
|
|
Дисперсия
|
215044,05
|
Дисперсия
|
306017,1725
|
|
Среднее
линейное отклонение
|
373,1
|
Среднее
линейное отклонение
|
426,14
|
|
Среднее
квадратическое отклонение
|
463,7284227
|
Среднее
квадратическое отклонение
|
553,188189
|
|
Коэффициент
вариации, %
|
17,04883907
|
Коэффициент
вариации, %
|
21,74952089
|
|
Структурный
коэффициент асимметрии К.Пирсона
|
-0,21025237
|
Структурный
коэффициент асимметрии К.Пирсона
|
0,015275091
|
3.
На основе рассчитанных показателей в предположении, что распределения единиц по
обоим признакам близки к нормальному, оценим:
а)
степень колеблемости значений признаков в совокупности;
Для
этого необходимо оценить коэффициентом вариации Vs
Принята
следующая оценочная шкала колеблемости признака:
0%<Vs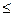 40% -
колеблемость незначительная;
40% -
колеблемость незначительная;
40%<
Vs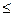 60% -
колеблемость средняя (умеренная); (6)
60% -
колеблемость средняя (умеренная); (6)
Vs>60% - колеблемость значительная.
Вывод: В данной
задаче:
Vs1=17,04883907%<40% - колеблемость
незначительная;
Vs2=21,74952089%<40% - колеблемость незначительная.
б)
степень однородности совокупности по изучаемым признакам. Для нормальных и
близких к нормальному распределений показатель Vs служит
индикатором однородности совокупности: принято считать, что при выполнимости
неравенства
Vs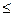 33% (7)
33% (7)
совокупность
является количественно однородной по данному признаку.
Вывод: Изучаемая совокупность является
качественно однородной по обоим признакам, так как для них выполняется условие Vs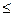 33% (для
первого признака Vs =17,04883907
дл второго Vs =21,74952089)
33% (для
первого признака Vs =17,04883907
дл второго Vs =21,74952089)
в)
устойчивость индивидуальных значений признаков;
Устойчивость
индивидуальных значений признаков оценим на основе сопоставления средних
отклонений – квадратического 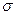 и линейного
и линейного 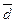 . В условиях распределений, близких к нормальному, между
показателями
. В условиях распределений, близких к нормальному, между
показателями 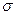 и
и 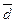 имеет место равенство:
имеет место равенство:
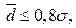 поэтому отношение
показателей
поэтому отношение
показателей 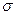 и
и 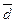 может служить
индикатором устойчивости данных.
может служить
индикатором устойчивости данных.
По первому
признаку: 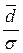 = 0,804566
= 0,804566
По второму
признаку: 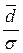 =0,770335
=0,770335

Вывод: Поскольку индикатор устойчивости
данных для признака «среднегодовая стоимостью производственных фондов» больше
0,8, то делаем вывод, что значение данного признака неустойчивы, в них имеются
«аномальные» выбросы. Поэтому, несмотря на визуальное обнаружение и исключение
нетипичных единиц наблюдений, некоторые
аномалии в первичных данных продолжают сохраняться. По второму признаку делаем
вывод об устойчивости значений признака.
г) количество попаданий индивидуальных
значений признаков в диапазоны (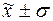 ), (
), (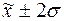 ), (
), (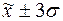 ). Сформируем следующую таблицу:
). Сформируем следующую таблицу:
Таблица 9
Распределение
значений признака по диапазонам рассеяния признака относительно 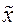
|
Границы диапазонов
|
Количество значений xi,
находящихся в каждой зане
|
|
1 признак
|
2 признак
|
1 признак
|
2 признак
|
|
(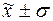 ) )
|
2256,27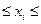 3183,73 3183,73
|
1990,26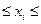 3096,64 3096,64
|
20
|
19
|
|
(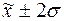 ) )
|
1792,55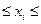 3647,45 3647,45
|
1437,07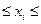 3649,82 3649,82
|
28
|
28
|
|
(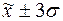 ) )
|
1328,82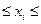 4111,185 4111,185
|
883,88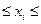 4203,01 4203,01
|
30
|
30
|
Сопоставление
полученных процентных соотношений рассеяния значений признаков по диапазонам с
ожидаемым по правилу «трех сигм» показывает, что в первый диапазон попадает
меньше значений. Соответственно по первому признаку – 66,7%, по второму – еще
меньше 63,3% против ожидаемых 68,3%. Во второй диапазон по обоим признакам
попадает по 93,3% значений, что также меньше вероятностной оценки - 95,4%. В
третьем диапазоне появляются все значения по обоим признакам (ожидаемое –
99,7%).
Вывод:
распределение данных по диапазонам близко к нормальному.
4.
Дадим сравнительную характеристику распределений
единиц совокупности по двум изучаемым признакам на основе анализа:
а)
Вариации признаков. Сравнение показателей вариации для двух изучаемых признаков
показывает, что по второму признаку (выпуск продукции) величины всех
показателей вариации выше:
ü
размах вариации 2340 против 1950 млн. руб.;
ü
дисперсия 306017,1725 против 215044,05;
ü
среднее линейное отклонение 426,14 против 373,1
млн.руб.;
ü
среднее квадратическое отклонение 553,188189 против 463,7284227
млн.руб.;
ü
коэффициент вариации 21,74952089 против
17,04883907%.
Вывод: степень
колеблемости значений второго признака выше.
б)
Количественной однородности единиц. Величина коэффициента вариации по признаку хотя и больше, но она не превышает
33%, следовательно, в обеих совокупностях единицы количественно однородны.
в)
Надежности (типичности) средних значений признаков. Количественная однородность
единиц первой совокупности означает, что индивидуальные значения среднегодовой
стоимости основных фондов мало отличаются друг от друга и средняя
арифметическая величина 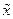 =2720 млн. руб. является надежной характеристикой данной
совокупности. Точно также и средняя величина выпуска продукции
=2720 млн. руб. является надежной характеристикой данной
совокупности. Точно также и средняя величина выпуска продукции 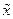 =2543,45 млн. руб. является типичной для своих индивидуальных
значений.
=2543,45 млн. руб. является типичной для своих индивидуальных
значений.
г) Симметричности распределений в центральной части ряда.
Для этого сравним величины структурного коэффициента
асимметрии К.Пирсона (Asп) между собой и с оценочной шкалой асимметричности (13)
|As|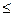 0,25 - асимметрия незначительная;
0,25 - асимметрия незначительная;
0,25<|As|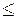 0,5 -
асимметрия заметная (умеренная); (13)
0,5 -
асимметрия заметная (умеренная); (13)
|As|>0,5 - асимметрия существенная.
Вывод: По первому
признаку Asп=-0,21. Следовательно, имеет место незначительная
левосторонняя асимметрия (Asп <0 и по модулю не превышает 0,25).
По
второму признаку
Asп=0,015 (Asп>0 и по модулю не превышает 0,25).
Следовательно, асимметрия правосторонняя, но ничтожно малая. Распределение
можно считать симметричным.
Кроме того, для первого признака справедливо неравенство:

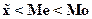 , 2720<2749,25<2817,5
, 2720<2749,25<2817,5
Это также указывает на левостороннюю асимметрию, т.е. вершина
кривой распределения немного сдвинута вправо, а левая ветвь кривой оказывается
длиннее правой. Для второго признака все три характеристики центра
распределения очень близки между собой, поэтому можно записать: 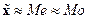 , 2543,45
, 2543,45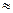 2525,25
2525,25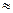 2535. Это подтверждает вывод о симметричности распределения.
2535. Это подтверждает вывод о симметричности распределения.
5.
Анализ полученного интервального вариационного ряда и формы гистограммы
показывает, что эмпирическое распределение имеет сходство (хотя и не строгое) с
нормальным распределением. Проявляется оно в том, что крайние значения признака
(близкие к Xmax
и Xmin)
встречаются много реже, чем серединные, гистограмма имеет одновершинную форму,
она приблизительно симметрична, так как ее «хвосты» не очень длинны (за
пределами интервала 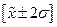 лежат по 6,7% вариантов), а в диапазоне
лежат по 6,7% вариантов), а в диапазоне 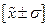 располагается основная масса единиц – 66,7%. Таким образом,
характер (тип) распределения единиц совокупности по признаку «среднегодовая
стоимость основных производственных фондов» можно считать близким к нормальному
(наблюдается незначительная левосторонняя асимметрия, что установлено в задании
4г.)
располагается основная масса единиц – 66,7%. Таким образом,
характер (тип) распределения единиц совокупности по признаку «среднегодовая
стоимость основных производственных фондов» можно считать близким к нормальному
(наблюдается незначительная левосторонняя асимметрия, что установлено в задании
4г.)
Для получения интервального ряда
значение моды рассчитаем по формуле:
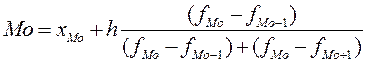
Модальный
интервал 2525-2915, следовательно xMo=2525,
величина модального интервала h=2915-2525=390,
частота модального интервала fMo=11,
частота предмодального интервала fMo-1=5, частота
послемодального интервала fMo+1=7.
Таким
образом, после расчета, Mo=2759 млн.руб.
Показатель моды, рассчитанный для интервального ряда данных (2759 млн.руб.) не
совпадает с аналогичным показателем для несгруппированных данных (2817,5
млн.руб.). Это объясняется разной методикой расчета.
По несгруппированным данным модой
является наиболее часто встречающийся вариант. Им оказалось значение признака 2817,5,
которое встретилось в совокупности три раза, другие значения присутствовали в
единственном числе. По сгруппированным данным величина моды зависит от нижней
границы, размера и частоты модального интервала, а также от предмодальной и
послемодальной частот.
Статистический анализ
генеральной совокупности
1. На основании таблицы 3 сформируем таблицу 10 для генеральных показателей
совокупности:
Таблица 10
Описательные
статистики генеральной совокупности
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Дисперсия
(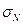 ) )
|
222459,3621
|
316569,4888
|
|
Среднее
квадратическое отклонение (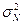 ) )
|
471,6559785
|
562,6450824
|
|
Ожидаемый
размах вариации признака (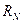 ) )
|
2829,93581
|
3375,870494
|
|
Коэффициент
эксцесса (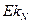 ) )
|
-0,344943844
|
-0.205332365
|
|
Коэффициент
асимметрии (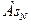 ) )
|
-0.152503649
|
0.042954448
|
Степень
расхождения между 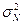
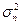 устанавливается по
формуле (16):
устанавливается по
формуле (16):
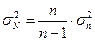 .
.
Поправочный
коэффициент n/(n-1)=30/(30-1)=30/29=1.034482758. Его значение близко к единице, следовательно,
степень расхождения между 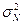 и
и 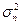 незначительная.
Степень расхождения между
незначительная.
Степень расхождения между 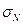 и
и 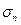 еще меньше и
составляет 1,017095255.
еще меньше и
составляет 1,017095255.
Определим
прогнозное значение размаха вариации признака в генеральной совокупности: 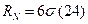
Степень
расхождения между 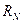 и
и 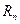
по первому признаку =2829,93581/1950
= 1,451249164;
по второму признаку = 3375,870494/2340=1,442679698.
Вывод: Прогнозное значение 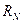 по первому признаку
превосходит
по первому признаку
превосходит 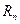 в 1,45 раза, по
второму – в 1,44 раза, т.е. степень расхождения между
в 1,45 раза, по
второму – в 1,44 раза, т.е. степень расхождения между 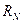 и
и 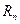 следует считать
существенной.
следует считать
существенной.
2. Для
изучаемых признаков рассчитать:
а)
Средние ошибки выборки (параметр Стандартная ошибка) рассчитаны и приведены в
табл. 3. «Описательные статистики»
б) Оценки
предельных ошибок выборки имеются в табл.3,4а, 4б. На основе этих оценок и
формулы (15) определим ожидаемые границы для генеральных средних, результаты
представим в таблице 11.
Таблица 11
Предельные ошибки выборки и ожидаемые границы для генеральной
совокупности
|
Доверительная
вероятность p
|
Коэффициент доверия
t
|
Предельные ошибки
выборки
|
Ожидаемые границы
для генеральных средних
|
|
Для первого
признака
|
Для второго
признака
|
Для первого
признака
|
Для второго
признака
|
|
0,683
|
1
|
87,67991917
|
104,5946147
|
2632,32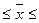 2807,68 2807,68
|
2438,85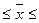 2648,04 2648,04
|
|
0,954
|
2
|
179,5277582
|
214,1611999
|
2540,47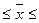 2899,52 2899,52
|
2329,29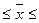 2757,61 2757,61
|
|
0,997
|
3
|
278,9520402
|
332,7658311
|
2441,04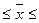 2998,95 2998,95
|
2210,68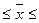 2876,21 2876,21
|
Ожидаемые границы для генеральных
средних вычисляются как среднее по признаку ± предельные ошибки
выборки для каждой доверительной вероятности
3. Рассчитать коэффициенты
асимметрии As и эксцесса Ek. На основе полученных оценок сделать вывод о степени близости
распределения единиц генеральной совокупности к нормальному распределению.
Поскольку распределение единиц
выборочной совокупности по каждому признаку близко к нормальному, выборка
является репрезентативной (значение показателей 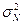 и
и 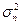 расходятся
незначительно) и при этом коэффициент асимметрии по обоим признакам меньше
0,25 (табл.3). Т.е. есть основание полагать, что распределение единиц
генеральной совокупности близко к нормальному распределению.
расходятся
незначительно) и при этом коэффициент асимметрии по обоим признакам меньше
0,25 (табл.3). Т.е. есть основание полагать, что распределение единиц
генеральной совокупности близко к нормальному распределению.
Коэффициент эксцесса вычисляется
только для симметричных или близких к ним распределений. В нашем случае для
обоих признаков он <0, следовательно вершина кривой эмпирического
распределения лежит несколько ниже вершины нормальной кривой, а форма кривой
более пологая по сравнению с нормальной. Это означает, что значения признака не
концентрируются в центральной части ряда, а достаточно равномерно рассеяны по
всему диапазону от Xmax
до Xmin.
Экономическое
содержание задач
статистического
исследования
1.
Типичны ли образующие выборку предприятия по значениям
изучаемых экономических показателей?
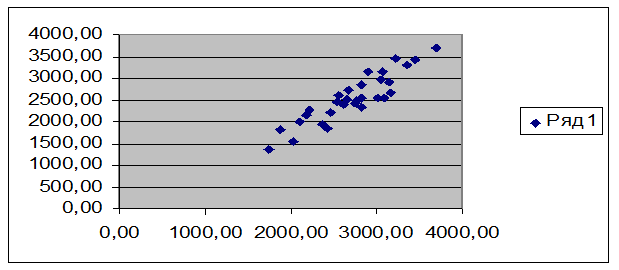
В
результате визуального анализа диаграмму рассеяния значений показателей, были
выделены 2 предприятия с резко выделяющимися характеристиками (см. табл.2): №31
с максимальной стоимостью основных производственных фондов (3695млн. руб.) и
минимальным выпуском продукции (975 млн. руб.) и №12 - с минимальной стоимостью
основных производственных фондов (1160 млн. руб.) и достаточно высоким выпуском
продукции (2925 млн. руб.). Остальные, образующие выборку предприятия, типичны
по значениям изучаемых экономических показателей.
2. Типичный уровень для предприятий
среднегодовой стоимости основных фондов – 2720млн. руб., а типичный уровень
выпуска продукции – 2543,45 млн.руб.
Наиболее
характерные для предприятий значения показателей представлены в таблице:
|
Границы диапазонов
|
Количество значений xi, находящихся в каждой зане
|
|
1 признак
|
2 признак
|
1 признак
|
2 признак
|
|
(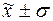 ) )
|
2256,27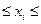 3183,73 3183,73
|
1990,26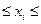 3096,64 3096,64
|
20
|
19
|
В 1 признак
входят 20 предприятий (№№2,3,4,6,7,9,10,13,14,17,18,19,20,22,24,25,26,28,29,30),
во 2 признаке 19 предприятий (№№1,2,3,4,6,8,9,13,14,17,18,20,24,25,26,28,
29,30,32).
3.
Насколько сильны различия в экономических характеристиках предприятий
выборочной совокупности? Можно ли утверждать, что выборка сформирована из
предприятий с достаточно близкими значениями по каждому из показателей?
Предприятия
достаточно однородны по обоим изучаемым экономическим характеристикам, т.к.
коэффициент вариации не превышает 33%. При этом по первому признаку выборка
сформирована из предприятий с более близкими значениями (Vσ=17,04883907%), чем по выпуску продукции (Vσ=21,74952089%). Максимальное расхождение в
значениях показателей:
·
по первому признаку – 1950 млн.руб.
·
по второму признаку – 2340 млн.руб.
4.
Какова структура предприятий выборочной совокупности по среднегодовой стоимости
основных фондов? Каков удельный вес предприятий с наибольшими, наименьшими и
типичными значениями данного показатели? Какие именно это предприятия?
Структура
предприятий выборочной совокупности по среднегодовой стоимости основных фондов
представлена в таблицы 7.
Удельный
вес предприятий с типичными значениями рассматриваемого показателя – 36,7%.
Модальный интервал – 2525-2915 млн.руб. В него вошли 11 предприятий
(№№3,4,6,7,9,13,14,17,25,26,28).
В группу с наименьшей стоимостью основных фондов 1745-2135
млн.руб. входят 4 предприятия (13,3%) (№№1,5,23,27).
В группу с наибольшей стоимостью основных фондов 3305-3695млн.руб.
входят 3 предприятия (10%) (№№11,16,21).
На
основе анализа можно сделать вывод о том, что большинство предприятий
сосредоточены в модальном интервале, то есть в интервале с наиболее типичными
значениями изучаемого показателя.
5. Носит ли распределение предприятий
по группам закономерный характер и какие предприятия (с более высокой или более
низкой стоимостью основных фондов) преобладают в совокупности?
Гистограмма
ряда распределения по среднегодовой стоимости основных фондов представлена на
рисунке 1. По гистограмме визуально
можно установить, что распределение предприятий по группам носит закономерный
характер. Судя по величине показателя асимметрии 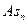 = -0,21025237, имеет место незначительная левосторонняя
асимметрия (
= -0,21025237, имеет место незначительная левосторонняя
асимметрия (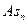 <0 и по абсолютной величине не превышает 0,25). Это
означает, что в совокупности чаще встречаются предприятия с более низкой
стоимостью основных фондов. Действительно, в 1-ой группе на одно предприятие
больше, чем в 5-ой.
<0 и по абсолютной величине не превышает 0,25). Это
означает, что в совокупности чаще встречаются предприятия с более низкой
стоимостью основных фондов. Действительно, в 1-ой группе на одно предприятие
больше, чем в 5-ой.
6.
Каковы ожидаемые средние величины среднегодовой стоимости основных фондов и
выпуска продукции на предприятиях корпорации в целом? Какое
максимальное расхождение в значениях показателя можно ожидать?
|
Доверительная
вероятность
|
Ожидаемые
границы для генеральных средних
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
0,683
|
2632,32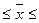 2807,68 2807,68
|
2438,85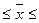 2648,04 2648,04
|
|
0,954
|
2540,47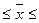 2899,52 2899,52
|
2329,29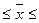 2757,61 2757,61
|
|
0,997
|
2441,04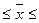 2998,95 2998,95
|
2210,68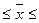 2876,21 2876,21
|
Максимальное
расхождение в значениях первого показателя можно ожидать в размере 2829,93581
млн.руб., второго – 3375,870494 млн.руб.