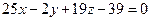1.     Вычислить определитель.

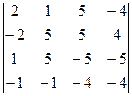
Решение:

Определитель будем вычислять с помощью свойств определителя.

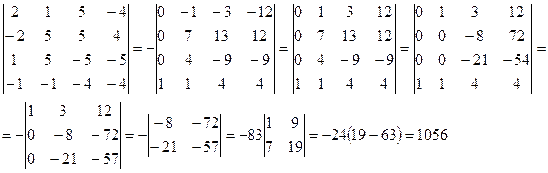
Ответ: 1056

2.     Найти произведение матриц.

а) 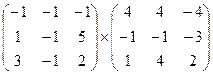       б)

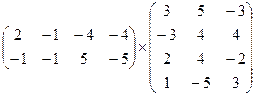
Решение:

а)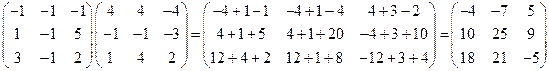

б)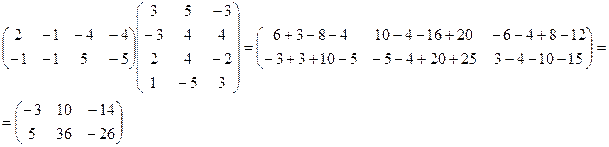

3.     Решить систему методом Крамера.

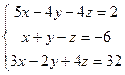
Решение:

Будем искать по формулам Крамера:

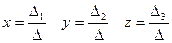
Найдем определители 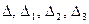 по методу треугольника.

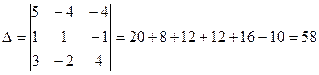
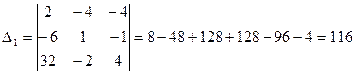
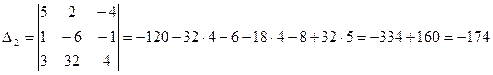
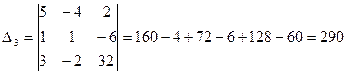
Тогда

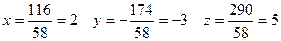
Ответ: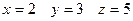

4.     Решить систему с помощью обратной матрицы.

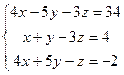
Решение:

Запишем систему в матричном виде:

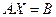
где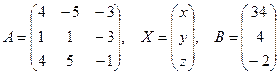

Тогда решение X будем искать по формуле:

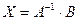
Найдем обратную матрицу :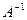

Вычислим определитель 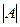 и алгебраические дополнения:

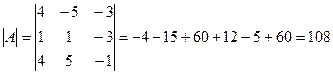
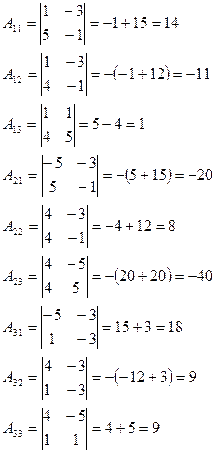
Составим присоединенную матрицу :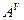

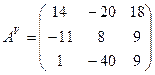
Обратную матрицу вычислим по формуле:

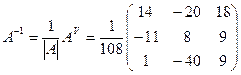
Теперь найдем решение системы:

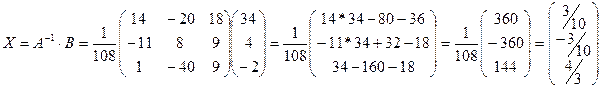
5.     Решить систему методом Гаусса.

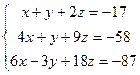
Решение:

Запишем расширенную матрицу системы и приведем к ступенчатому виду:

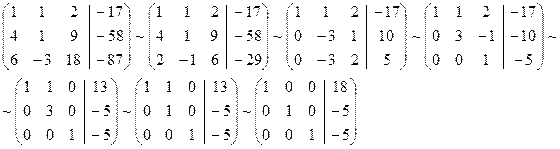
Ответ: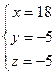

6.     Решить две системы с одинаковыми главными матрицами.

           

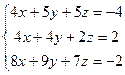
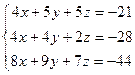
Решение:

Найдем решение системы с помощью метода Гаусса:

Решение первой системы:

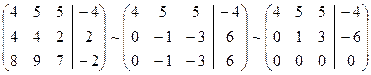
За базисные неизвестные примем x и y, за свободную z. Выразим через свободные неизвестные базисные:

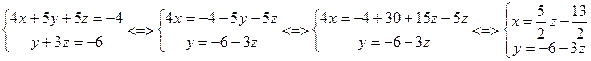
Тогда общее решение системы:

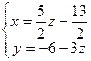
Аналогично решим вторую систему:

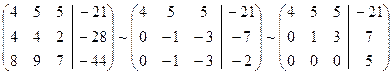
За базисные неизвестные примем x и y, за свободную z. Выразим через свободные неизвестные базисные:

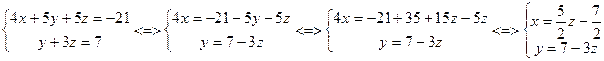Тогда общее решение системы:

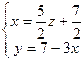
7.     Ниже даны координаты трех точек на плоскости А, В, С.

Выполнить следующие действия:

а) Написать уравнение прямой АВ;

б) Вычислить угол между прямой АВ и прямой ;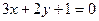

в) Через точку С провести прямую, параллельную прямой АВ;

г) Через точку С провести прямую, перпендикулярную прямой АВ;

д) Найти проекцию точки С на прямую АВ;

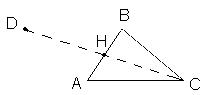
е) Найти координату точки D, симметричной точке С относительно прямой АВ;

ж) Вычислить площадь треугольника АВС.

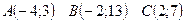
Решение:

а) Напишем уравнение прямой АВ:

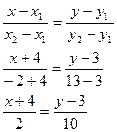
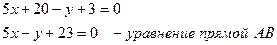
б) Угол между прямыми найдем по формуле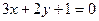

в) Воспользуемся условием параллельности двух прямых:

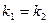
Угловой коэффициент прямой АВ равен:

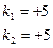
Составим уравнение прямой, параллельной АВ и проходящей через точку С:

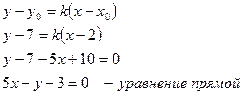
г) Воспользуемся условием перпендикулярности двух прямых:

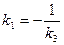
Тогда

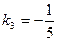
Аналогично составляем уравнение прямой, перпендикулярной АВ:

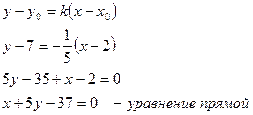
д) Найдем координаты точки Н, точки пересечения прямой АВ и СН:

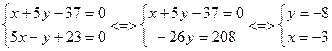
Координаты точки Н(-3;-8)

Тогда проекция равна:

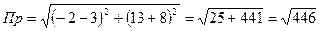
е) Точка H является серединой отрезка СD:

 

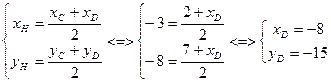
Ответ: D(-8;-15)

ж) Вычислим площадь АВС:

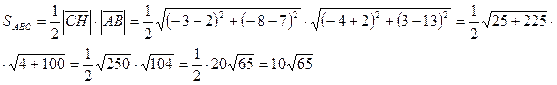
8.     Ниже даны координаты вершин пирамиды ABCD.

Найти:

а) Длину ребра АВ;

б) Косинус угла между ребрами АВ и AD;

в) Площадь грани АВС;

г) Объем пирамиды;

д) Уравнение прямой АВ;

е) Уравнение плоскости АВС;

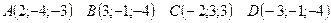
Решение:

а) Найдем координаты вектора :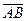

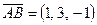
Тогда его длина равна:

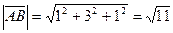
б) Найдем координаты вектора AD и его длину:

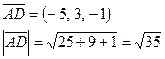
Найдем косинус:

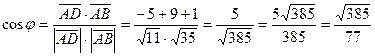
в) Найдем координаты вектора :

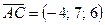
Далее найдем векторное произведение векторов 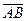и :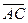

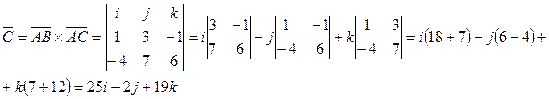
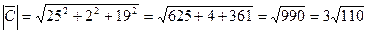
Тогда

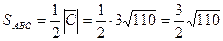
г) Найдем объем пирамиды:

Воспользуемся смешанным произведением:

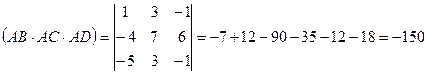
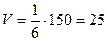
д) Найдем уравнение прямой АВ:

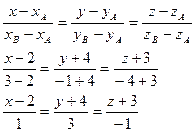
е) Найдем уравнение плоскости АВС:

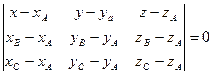
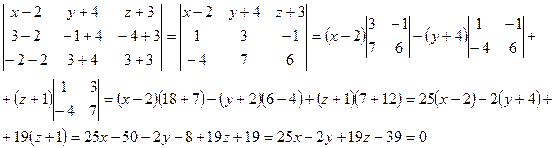
Ответ: