Задача №1
В таблице 1 содержатся
данные о числе Y жителей N = 40 городов страны. Города разделены на два слоя: в первом слое – 10
наиболее крупных, во втором – все остальные города. С помощью таблицы случайных
чисел сформировать следующие выборки, состоящие из n = 16 городов:
1. расслоенную выборку с
пропорциональным размещением;
2. расслоенную выборку, содержащую
одинаковое число единиц каждого слоя;
3. простую
(нерасслоенную) случайную выборку.
Найти по каждой из этих
выборок:
а) оценку среднего числа
жителей всех 40 городов;
б) среднюю ошибку и 95%
доверительный интервал для этой оценки;
в) оценку суммарного
числа жителей всех 40 городов;
г) среднюю ошибку и 95%
доверительный интервал для этой оценки.
Найти истинное значение
среднего и суммарного значения по всем 40 городам. Какая выборка дала более
точные результаты?
Таблица 1 (тыс. жит.):
|
№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Y
|
915
|
706
|
666
|
575
|
533
|
519
|
505
|
499
|
442
|
433
|
|
№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Y
|
432
|
414
|
376
|
374
|
356
|
353
|
334
|
326
|
310
|
298
|
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|
290
|
281
|
279
|
277
|
271
|
256
|
254
|
250
|
248
|
1383
|
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
|
239
|
231
|
236
|
234
|
231
|
228
|
226
|
224
|
222
|
218
|
Решение:
1. Построим расслоенную
выборку с пропорциональным размещением.
Наиболее широко
применяемый способ заключается в том, что объемы выборок из групп
устанавливаются пропорционально объемам соответствующих типических групп, т. е.
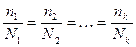
В итоге для расчетов
получается такая формула:
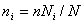
где ni - объем выборки из i - й типической группы; n - общий объем выборки из генеральной
совокупности; Ni - объем i - й типической группы; N - объем генеральной совокупности.
В нашем случае из первой
группы мы должны выбрать:
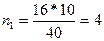
из второй:
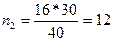
С помощью таблицы
случайных величин отбираем числа:
Для первой группы – 1, 9,
2, 5
Для второй группы- 22,9,26,2,1,27,25,20,4,11,15,12
Среднее число жителей для
первой группы:
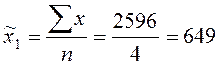
Среднее число жителей для
второй группы:
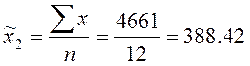
Тогда общая средняя
равна:
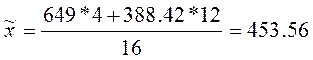
Дисперсия среднего
числа жителей первой группы равна:
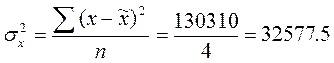
Второй группы:
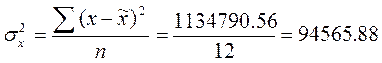
Средняя ошибка выборочной
средней определяется по следующей формуле:
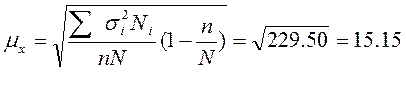
Предельная ошибка
Δ вычисляется на основе знания средней ошибки μ по формуле:
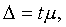
где t - величина, вычисляемая по специальной таблице.
Пусть Р=0,95. Этому
значению Р по табл. 1 приложения соответствует t=2. имеем Δ=2*15,15=30,3
т. е. предельная ошибка выборки равна приблизительно 30,3.
Переходим к определению
пределов. Чтобы вычислить нижний предел, нужно из выборочной средней вычесть
предельную ошибку выборки:
453,56—30,3=423,26
Верхний предел
получаем, прибавив к выборочной средней предельную ошибку:
453,56+30,3=483,86
Тогда имеем следующие
пределы для генеральной средней 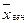 :
:
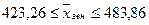
2. Построим расслоенную
выборку, содержащую одинаковое число единиц каждого слоя.
С помощью таблицы
случайных величин отбираем числа:
Для первой группы – 1, 9,
2, 5, 6, 3, 7, 4;
Для второй группы- 9,26,2,27,25,4,11,12.
Среднее число жителей для
первой группы:
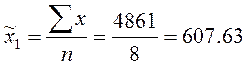
Среднее число жителей для
второй группы:
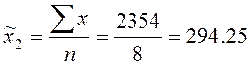
Тогда общая средняя
равна:
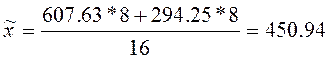
Дисперсия среднего
числа жителей первой группы равна:
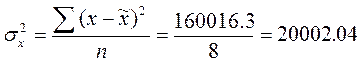
Второй группы:
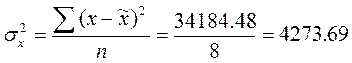
Средняя ошибка выборочной
средней определяется по следующей формуле:
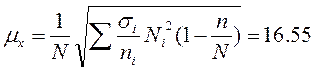
Предельная ошибка
выборки приблизительно равна:
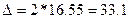
Переходим к определению
пределов:
Нижний предел:
450,94-33,1=417,84.
Верхний предел:
450,94+33,1=484,04.
Тогда имеем следующие
пределы для генеральной средней 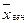 :
:
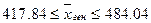
3. Построим простую
(нерасслоенную) случайную выборку.
Из таблицы случайных
чисел отбираем числа, не превосходящие 40, до тех пор, пока не наберем нужных
16 чисел. Получаем:
10, 9, 25, 33, 1, 35, 34,
37, 20, 5, 24, 8, 19,3, 23, 7
Выписанные числа будем
считать порядковыми номерами тех элементов генеральной совокупности, которые
попали в выборку.
Для дальнейшей работы
полезно полученные числа расположить в возрастающем порядке.
|
№ города
|
1
|
3
|
5
|
7
|
8
|
9
|
10
|
19
|
|
Y
|
915
|
666
|
533
|
505
|
499
|
442
|
433
|
310
|
|
№ города
|
20
|
23
|
24
|
25
|
33
|
34
|
35
|
37
|
|
Y
|
298
|
279
|
374
|
271
|
236
|
234
|
231
|
226
|
Среднее число жителей:
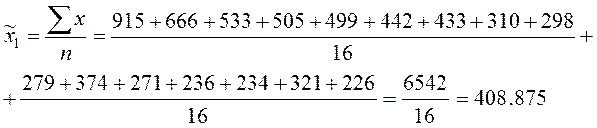
Дисперсия среднего
числа жителей равна:
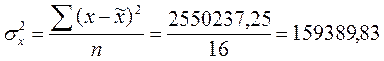
Средняя ошибка выборочной
средней определяется по следующей формуле:
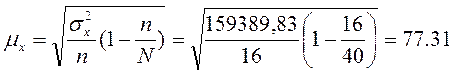 ,
,
где n - численность выборки;
N - численность
генеральной совокупности;
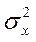 - дисперсия признака x.
- дисперсия признака x.
Предельная ошибка
выборки приблизительно равна:
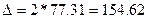
Переходим к определению
пределов:
Нижний предел:
408,875-154,62=254,255
Верхний предел:
408,875+154,62=563,495
Тогда имеем следующие
пределы для генеральной средней 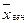 :
:
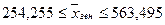
Истинное значение
среднего значения по всем 40 городам равно 386,35. Третья выборка дала более
точный результат.
Задача №2
Опытный фермер оценивает
на глаз урожай персиков, 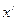 , с каждого дерева в саду с N = V деревьев. Он определил, что их общий
вес
, с каждого дерева в саду с N = V деревьев. Он определил, что их общий
вес 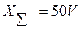 фунтов. Для некоторой простой случайной выборки объемом n = 10 деревьев все плоды были собраны
и взвешены, что дало следующие результаты (см. таблицу 2). Вычислите оценку по
регрессии действительного веса
фунтов. Для некоторой простой случайной выборки объемом n = 10 деревьев все плоды были собраны
и взвешены, что дало следующие результаты (см. таблицу 2). Вычислите оценку по
регрессии действительного веса 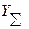 и найдите её стандартную ошибку и 95% доверительный интервал.
и найдите её стандартную ошибку и 95% доверительный интервал.
Таблица 2:
|
Номер дерева
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Действительный вес, yi
|
71,98
|
49,56
|
59
|
68,44
|
79,06
|
53,1
|
46,02
|
67,26
|
83,78
|
74,34
|
|
Оценка веса, xi
|
69,62
|
55,46
|
61,36
|
70,8
|
79,06
|
56,64
|
51,92
|
68,44
|
89,68
|
68,44
|
Решение:
Составим уравнение
регрессии:
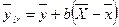 ,
,
где b – коэффициент регрессии:
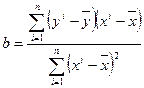
Для вычисления
коэффициента регрессии составим вспомогательную таблицу:
|
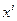
|
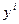
|
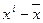
|
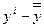
|
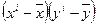
|
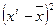
|
|
69,62
|
71,98
|
2,478
|
6,726
|
16,66703
|
6,140484
|
|
55,46
|
49,56
|
-11,682
|
-15,694
|
183,3373
|
136,4691
|
|
61,36
|
59
|
-5,782
|
-6,254
|
36,16063
|
33,43152
|
|
70,8
|
68,44
|
3,658
|
3,186
|
11,65439
|
13,38096
|
|
79,06
|
79,06
|
11,918
|
13,806
|
164,5399
|
142,0387
|
|
56,64
|
51,3
|
-10,502
|
-12,154
|
127,6413
|
110,292
|
|
51,92
|
46,02
|
-15,222
|
-19,234
|
292,7799
|
231,7093
|
|
68,44
|
67,26
|
1,298
|
2,006
|
2,603788
|
1,684804
|
|
89,68
|
83,78
|
22,538
|
18,256
|
417,539
|
507,9614
|
|
68,44
|
74,34
|
1,298
|
9,086
|
11,79363
|
1,684804
|
|
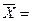 67,142 67,142
|
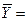 65,254 65,254
|
|
|
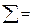 1264,717 1264,717
|
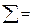 1184,793 1184,793
|
Коэффициент регрессии b = 1,067.
Тогда оценка по регрессии суммарного
значения 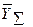 будет равна:
будет равна: 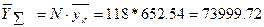 .
.
Найдем 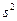 :
:
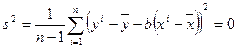
Дисперсия
величины 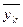 вычисляется по
приближенной формуле:
вычисляется по
приближенной формуле: 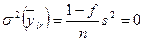
Стандартная ошибка
величины 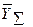 равна:
равна: 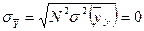 .
.