Доработка
Задание
1
Взята ссуда на 10 лет в
сумме 25000 (у.д.е.) под 25 процентов годовых, начисляемых на непогашенный
остаток. Возвращать нужно равными суммами в конце каждого года (начисление
процентов совпадает со временем возврата). Требуется: составить модель
погашения ссуды; вычислить величину годового платежа; определить величину всей
возвращаемой суммы и величину общей суммы процентного платежа; сравнить данный
вариант с вариантом возврата ссуды вместе с процентами в конце срока операции.
Решение:
1) Модель погашения ссуды следующая
(((((((((25000×1.25–CF)×1.25-CF)×1.25-CF)×1.25-CF)×1.25-CF)×1.25-CF)×1.25-
-CF)×1.25-CF)×1.25-CF)-CF=0.
2) Величина годового
платежа:
.
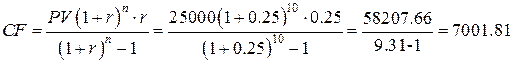3) Общая сумма платежа
7001,81×10=70018,1 у.д.е.
Общая сумма процентного
платежа составит
7001,81×10-25000=
45018.14 у.д.е.
4) По второму варианту,
при возврате в конце срока операции по окончании 10 лет возвращаемая сумма
составит
25000×(1+10×0,25)=87500
у.д.е. против 70018,1 у.д.е. по первому варианту, т.е. первый вариант выгоднее
для ссудозаемщика.
При этом процентный
платеж составит 25000×0,25×10= 62500 у.д.е.
Таким образом, возвращать
ссуду с начислением процентов на непогашенный остаток выгоднее, чем с
начислением процентов в конце срока.
Задание 2
Определить будущую
стоимость обыкновенного аннуитета накопления с реальной доходностью 20
процентов в год с учетом инфляции (ежегодный темп инфляции составляет 15
процентов), если ежегодный вклад пренумерандо 1700 (у.д.е.), а срок операции 7
лет.
Указание. Наращение
производить по номинальной процентной ставке, исчисленной по формуле Фишера.
Решение.
Пусть r – номинальная ставка процентов, х =
0,2 – реальная доходность,
у = 0,15 – ежегодный темп инфляции, n = 7 – срок операции, s = 1700 – ежегодный вклад пренумерандо;
S – искомая
стоимость.
Найдем значение
номинальной ставки процентов
r = х + у + х×у
= 0.2+0.15+0.2·0.15 = 0.35+0.03 = 0.38, т.е. 38%
Искомая стоимость будет
равна.
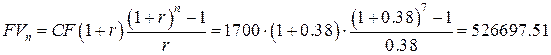у.д.е.
Задание 4
Предприятие рассматривает
инвестиционный проект, первоначальные инвестиции по которому I0=20000
(у.д.е.). Ожидается, что реализация проекта в течение 5 лет обеспечит получение
чистого дохода по годам постумерандо в объемах (у.д.е.): CF1=7000, CF2=9000, CF3=12000, CF4=11000, CF5=8000. Принятая ежегодная норма (ставка) дисконта d=15
процентов постоянна в течение всех лет экономической жизни проекта. Требуется:
1) оценить экономическую эффективность проекта, вычислив NPV, PI; 2) сравнить
данный проект с альтернативным, у которого Iа=30000, NPVа=7250,
а срок экономической жизни тоже 5 лет.
Решение:
Экономическая
эффективность проекта по показателям NPV и PI:
= 
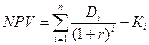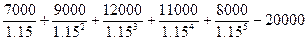= 11049.14 у.д.е.
= 
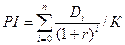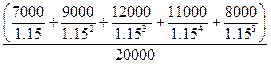= 1.5525
Поскольку NPV>0 и PI>1, то проект можно считать
экономически выгодным.
При сравнении проекта с
альтернативным, выясняется, что, поскольку у первого проекта показатель NPV больше. Сравним значения РIа
и РI.
= 
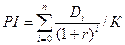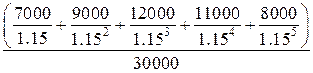= 1.035.
Поскольку РIа <
РI и NPVа < NPV, то первый проект выгоднее, хотя оба проекта
следует признать рентабельными.
Задание 7
Используя модель САРМ и
формулу расчета стоимости (цены) акции компании i, произвести вычисления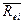 
и РО, а также
и 
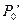по следующим данным:
|
Первоначальные значения
|
Новые значения
|
|
Номер варианта
|
Rf
(%)
|
 (%)
|
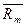βi
|
qi
|
Di
|
Rf’
(%)
|
 ’ (%)
|
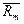βi’
|
qi’
|
Di’
|
|
5
|
9
|
14
|
0.9
|
0.03
|
2
|
7
|
13
|
0.8
|
0.02
|
2
|
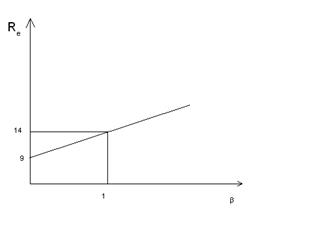
Построить график модели
рынка по первоначальным значениям, определить премии за риски.
Решение:
Общий вид модели САРМ.
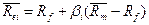
Подставив значения,
получим
=15.3
Стоимость акций в
первоначальном значении
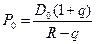
Подставив значения,
получим
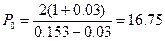
Для новых значений
получим:
Общий вид модели САРМ.
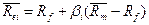
Подставив значения,
получим
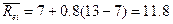
Стоимость акций в новом
значении
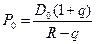
Подставив значения,
получим
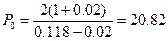
Уровень премии за риск
при первоначальном варианте вычисляется: 
; тогда как при новых значениях этот показатель: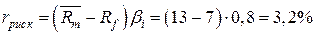 
.