Министерство образования РФ
Всероссийский заочный
финансово-экономический институт
Кафедра статистика
КУРСОВАЯ РАБОТА
По дисциплине «Статистика»
На тему
«Статистическое изучение страхового
рынка»
Вариант № 20
Исполнитель: Грачёва
Ю.А.
Специальность:
Бухучет, анализ и аудит
Группа: вечерняя
№ зачетной
книжки: 06УББ02694
Руководитель: Леонова
С.Н.
Орел
2008
Оглавление
Введение___________________________________________________3
1. Статистическое изучение страхового рынка
1.1. Предмет
статистики страхования. Особенности
функционирования страхового рынка______________________5
1.2. Виды, формы страхования и система показателей
статистики страхования____________________________________________9
1.3. Методы расчета тарифных ставок в рисковых
видах страхования___________________________________________17
2. Расчетная часть__________________________________________22
3. Аналитическая часть_____________________________________ 45
Заключение________________________________________________48
Список использованной литературы_________________________ 49
Введение
В странах с развитой
рыночной экономикой страхование является одним из стратегических секторов
экономики. Страхование обеспечивает социально-экономическую стабильность в обществе,
так как гарантирует собственникам возмещение ущерба при гибели или повреждении
имущества и потере дохода. Роль страхования проявляется, прежде всего, на
микроэкономическом уровне, конкретные договоры страхования заключаются юридическими
и физическими лицами с целью защиты своих имущественных интересов. При
возникновении крупных природных или техногенных катастроф, охватывающих
огромные территории, нарушающих деятельность сотен предприятий, угрожающих
жизни тысяч жителей, возмещение соответствующего ущерба через систему
страхования имеет макроэкономические последствия. Макроэкономические пропорции
развития ведущих государств мира во многом определяют огромные инвестиционные ресурсы
страховых компаний.
Современное рыночное
общество невозможно себе представить без страхования как особого вида
экономических отношений. Существует прямая связь между уровнем благосостояния
общества, степенью развития рыночных отношений и уровнем развития страхования.
Страхование - необходимый
элемент производственных отношений. Оно связано с возмещением материальных
потерь в процессе общественного производства. Рисковый характер общественного
производства, порождает отношения между людьми по предупреждению, преодолению,
локализации и по безусловному возмещению нанесенного ущерба. Однако предприятия
и организации различных форм собственности, выступающие в качестве
страхователей, испытывают потребность не только в возмещении ущерба,
выражающегося в гибели или повреждении основных фондов и оборотных средств, но
и в компенсации недополученной прибыли или дополнительных расходов из-за
вынужденных простоев (неритмичные поставки сырья, неплатежеспособность оптовых
покупателей). Именно поэтому государственная политика в области страхования
должна иметь стимулирующее воздействие на данный сегмент экономики.
Многовековой опыт и история страхования убедительно доказали, что оно является
мощным фактором положительного воздействия на экономику. Однако на пути
развития страхования в России имеются разнообразные проблемы, которые могут
быть решены лишь при наличии соответствующих условий.
Для реализации
возможностей страховой отрасли нужна активная государственная поддержка и, чем
быстрее государство осознает роль страхования как стратегического сектора
экономики, тем скорее в России будет осуществлен переход к
социально-ориентировочному рыночному росту.
Экономическая сущность страхования,
заключается в формировании страховщиком денежных фондов из уплачиваемых
страхователями страховых взносов (премий), предназначенных для производства
страховых выплат страхователям, застрахованным, «третьим» лицам или
выгодоприобретателем при наступлении страховых случаев, оговоренных в договоре
страхования.
В данной
курсовой работе мной будут рассмотрены такие вопросы как: понятие страхового
рынка и особенности его функционирования, виды, формы страхования и система
показателей статистики страхования, методы расчета тарифных ставок в рисковых
видах страхования.
Целью
расчетной части является
изучение состава и структуры выборочной совокупности страховых организаций. В
аналитической части анализируется страховой рынок, на примере страховых сборов
премий за 2000-2006 года по всему рынку.
Для выполнения математических
расчетов курсовой работы мной были использованы следующие программы: «MS Excel», «OLIMP».
1. Статистическое изучение страхового рынка
1.1. Предмет статистики страхования. Особенности
функционирования страхового рынка
Статистика страхования
является составной частью финансовой статистики.
Страхование – это система экономических
отношений, включающая образование специального фонда (страхового фонда) и его
использование (распределение и перераспределение).
Особенности
страхования
-
денежные отношения в страховании связаны с возможностью наступления страховых
случаев, наносящих ущерб;
-
при страховании нанесенный ущерб распределяется между участниками страхования;
-
при страховании ущерб перераспределяется между территориями и во времени;
-
страхование характеризуется возвратностью средств, внесенных в страховой фонд.
Предмет статистика
страхования - количественная сторона системы экономических отношений, которые
возникают в процессе осуществления страховой деятельности.
Страхование - это такой вид
необходимой общественно-полезной деятельности, при которой гражданин и
организация заранее страхуют себя от неблагоприятных последствий в сфере их
материальных и личных нематериальных благ путём внесения денежных взносов в
особую специализированную организацию (страховщика), оказывающей страховые
услуги, а эта организация при наступлении указанных последствий выплачивает за
счёт средств этого фонда страхователю или иному лицу обусловленную сумму. Объективная
потребность в страховании обуславливается тем, что убытки подчас возникают
вследствие разрушительных факторов, вообще не подконтрольных человеку
(стихийных сил природы), во всяком случае не влекут чей-либо
гражданско-правовой ответственности. В подобной ситуации бывает невозможно
взыскивать убытки с кого бы то ни было, и они “оседают” в имущественной сфере
самого потерпевшего. Заранее созданный страховой фонд может быть источником
возмещения ущерба. Страхование целесообразно только тогда, когда
предусмотренные правоотношениями страхователя и страховщика страховые события
(риски) вызывают значительную потребность в деньгах. Так, например, физическое
лицо, у которого эта потребность возникает, как правило, не может покрыть её из
собственных средств без чувствительного ограничения своего жизненного уровня.
Услуги страхования
распространяются на страховом рынке.
Страховой рынок- это особая сфера денежных отношений, где объектом
купли-продажи выступает специфическая услуга- страховая защита, формируется
предложение и спрос на нее. Объектом купли-продажи на страховом рынке выступает
страховая защита имущественных и других интересов.
Субъекты страхового рынка
Российской Федерации
Страховщик — юридическое лицо любой организационно-правовой формы,
предусмотренной законодательством РФ, созданное для осуществления страховой
деятельности и получившее в установленном законом порядке лицензию на эту
деятельность на территории России. Страховщиками могут быть государственные,
акционерные, частные или совместные страховые организации. Страховщики могут
осуществлять страховую деятельность напрямую или через страховых агентов и
страховых брокеров.
Страхователь (полисодержатель) – дееспособные физические или
юридические лица, которые заключают договор и уплачивают страховые взносы и тем
самым вступают в конкретные страховые отношения со страховщиком. Страхователями могут быть как
резиденты и нерезиденты, так и лица без гражданства, представляющие различные
типы собственности, различные отрасли (сектора) экономики. Основная задача страхователя состоит
в осуществлении регулярных страховых взносов (премий, платежей).
Страховые агенты - физические или юридические лица, осуществляющие свою
деятельность от имени страховщика и по его поручению в соответствии с
предоставленными полномочиями.
Страховые брокеры - физические или юридические лица, зарегистрированные в
установленном порядке в качестве предпринимателей, осуществляющие посредническую
деятельность по страхованию от своего имени на основании поручений страхователя
или страховщика. Страховой брокер:
·
представляет
интересы клиента;
·
действует
как консультант своего клиента и информирует его о диапазоне предоставляемых
компанией доступных страховых услуг;
·
ведет
переговоры от имени своего клиента с целью достижения приемлемого компромисса
между размером страхового покрытия и стоимостью страхования в пользу клиента,
иными словами, обеспечивает полную цепочку услуг — от привлечения клиента и размещения
а до урегулирования в случае возникновения страхового случая;
·
обеспечивает
максимально (оптимально) высокий стандарт распределения а и дает гарантии
клиенту, что при наступлении страхового случая он будет достаточно обеспечен.
Страховые актуарии – граждане РФ, имеющие квалификационный аттестат и
осуществляющие на основе договора со страховщиком деятельность по расчетам
страховых тарифов, страховых резервов и т.д.
Застрахованные - лица, участвующие в личном страховании, чья жизнь, здоровье
и трудоспособность являются объектом страховой защиты. Застрахованный может
быть одновременно страхователем, если заключает договор в отношении самого
себя.
Государственный надзор за
деятельностью субъектов страхового рынка осуществляет Федеральная служба
страхового надзора.
Классификация страхования
по объектам страховой защиты
По форме проведения
различают добровольное и обязательное;
По организации:
государственное, акционерное, медицинское и взаимное;
По отраслевому признаку:
личное, имущественное и ответственности.
Таким
образом, можно сделать вывод, что страхование - это способ возмещения убытков,
которые потерпело физическое или юридическое лицо, посредством их распределения
между многими лицами.
1.2. Виды, формы страхования и система показателей статистики
страхования
Классификация
страхования представляет собой научную систему деления страхования на сферы
деятельности, отрасли, под отрасли, виды и звенья.
По
форме организации страхование выступает как государственное, акционерное,
взаимное.
Государственное
страхование представляет собой организационную
форму, где в качестве страховщика выступает государство в лице специально
уполномоченных на это организаций. В круг интересов государства входит его
монополия на проведение любых или отдельных видов страхования (определённых
законом “о статусе страховой деятельности”).
Акционерное
страхование - негосударственная организационная форма,
где в качестве страховщика выступает частный капитал в виде акционерного общества,
уставной фонд который формируется из акций (облигаций) и других ценных бумаг,
принадлежащих юридическим и физическим лицам, что позволяет при сравнительно
ограниченных средствах быстро развернуть эффективную работу страховых компаний.
Взаимное
страхование - негосударственная организационная форма,
которая выражает договорённость между группой физических, юридических лиц о
возмещении друг другу будущих возможных убытков в определённых долях согласно
принятым условиям. Реализуется через общество взаимного страхования, которое
является страховой организацией некоммерческого типа, т.е. не преследует целей
извлечения прибыли из созданного страхового предприятия. Это крупная
организационная форма проведения страхования. Общество взаимного страхования
выступает как объединение физических или юридических лиц, созданное на основе
добровольного соглашения между ними для страховой защиты своих имущественных
интересов. Общество взаимного страхования является юридическим лицом и отвечает
по своим обязательствам всем своим имуществом. Каждый страхователь является
членом-пайщиком общества взаимного страхования. Минимальное количество
членов-пайщиков определяется уставом общества.
Медицинское
страхование - особая организационная форма страховой
деятельности. В Российской Федерации выступает как форма социальной защиты
интересов населения в охране здоровья. Цель его - гарантировать гражданам при
возникновении страхового случая получение медицинской помощи за счет накопления
средств (в том числе в государственной и муниципальной системах
здравоохранения) и финансировать профилактические мероприятия (диспансеризацию,
вакцинацию и др.). В качестве субъектов медицинского страхования выступают
гражданин, страхователь, страховая медицинская организация (страховщик),
медицинское учреждение (поликлиника, больница и др.).
Исходя
из страхового признака выделяют личное, имущественное страхование, страхование
ответственности и страхование экономических рисков. Необходимость выделения
четырех отраслей страхования характерна для Российского национального
страхового рынка. Подобная классификация определяется перечнем объектов и
рисками, подлежащими страхованию.
Личное
страхование трактуется как отрасль страхования, где
в качестве объектов страхования выступают жизнь, здоровье и трудоспособность
человека. Личное страхование подразделяется на страхование жизни и страхование
от несчастных случаев, сочетает рисковую и сберегательную функции, в том числе
за счет выдачи ссуд под залог страхового полиса.
Имущественное
страхование - отрасль страхования, в которой объектом
страховых правоотношений выступает имущество в различных видах; его
экономическое назначение - возмещение ущерба, возникшего вследствие страхового
случая. Застрахованным может быть имущество как являющееся собственностью
страхователя, так и находящееся в его владении, пользовании, распоряжении.
Страхователями выступают не только собственники имущества, но и другие
юридические и физические лица, несущие ответственность за его сохранность.
Страхование
ответственности - отрасль страхования, где объектом
выступает ответственность перед третьими (физическими и юридическими) лицами,
которым может быть причинен ущерб (вред) вследствие какого-либо действия или
бездействия страхователя. Через страхование ответственности реализуется
страховая защита экономических интересов возможных причинителей вреда, которые
в каждом данном страховом случае находят своё конкретное денежное выражение. В
страховании ответственности выделяют следующие подотрасли: страхование
задолжности и страхование на случай возмещение вреда, которое называют также
страхованием гражданской ответственности.
В
страховании экономических рисков (предпринимательских
рисков) выделяются две подотрасли: страхование риска прямых и косвенных потерь.
К прямым потерям могут быть отнесены, например, потери от недополучения прибыли,
убытки от простоев оборудования вследствие недопоставок сырья, материалов и
комплектующих изделий, забастовок и других объективных причин. Косвенные -
страхование упущенной выгоды, банкротство предприятия и др.
По
форме проведения страхование может быть обязательным (в силу закона) и
добровольным.
Инициатором
обязательного страхования является государство, которое в форме закона
обязывает юридических и физических лиц вносить средства для обеспечения
общественных интересов. Добровольное -замкнутая раскладка ущерба между
членами страхового общества исходя из установленных правовых норм. Инициатором
добровольного страхования выступают хозяйствующие субъекты, физические и
юридические лица.
Государство
устанавливает обязательную форму страхования, когда страховая защита тех
или иных объектов связана с интересами не только отдельных страхователей, но и
всего общества. Обязательное страхование проводится на основе соответствующих
законодательных актов, в которых предусмотрены: перечень объектов, подлежащих страхованию;
объем страховой ответственности; уровень (норма)страхового обеспечения,
основные права и обязанности сторон, участвующих в страховании; порядок
установления тарифных ставок страховых платежей и некоторые другие вопросы.
Закон
определяет круг страховых организаций, которым поручается проведение
обязательного страхования. При обязательном страховании достигается полнота
объектов страхования. С другой стороны, обязательная форма страхования
исключает выборочность отдельных объектов страхования. Тем самым имеется
возможность за счет максимального охвата объектов страхования при обязательной
форме его проведения применять минимальные тарифные ставки, добиваться высокой
финансовой устойчивости страховых операций.
Добровольное
страхование - одна из форм страхования. В отличие от
обязательного страхования возникает только на основе добровольно заключаемого
договора между страхователем и страховщиком. Часто при заключении такого
договора между сторонами участвует посредник в виде страхового брокера или страхового
агента. Договор страхования удостоверяется страховым полисом. Нормативную базу
для организации и проведения добровольного страхования создает страховое
законодательство. Исходя из законодательной базы формируются условия или
правила отдельных видов добровольного страхования. Эти правила и условия,
разрабатываемые страховщиком, подлежат обязательному лицензированию со стороны
органа государственного страхового надзора.
Добровольное
страхование имеет, как правило, заранее оговоренный определенный срок страхования.
Начало и окончание срока страхования указывается в договоре с особой точностью,
так как страховщик несет страховую ответственность только в период страхования.
Договор страхования обязательно заключается в письменной форме.
По
добровольному страхованию можно обеспечить непрерывность страхования при
своевременном возобновлении договора на новый срок. Добровольное страхование
вступает в силу лишь после уплаты страхового взноса (страховой премии). Причем
долгосрочный договор добровольного страхования действует, если взносы
уплачиваются страхователем периодически (ежемесячно, ежеквартально) или
единовременно ( один раз в год ).
Договоры
добровольного страхования имущества или личного страхования являются частью
гражданских правоотношений и входят в число возмездных договорных обязательств.
По такому договору одна сторона обязана уплатить другой стороне обусловленную
сумму взносов. В свою очередь другая сторона готова оказать оговоренную в
договоре страховую услугу. По договору страхования услуга состоит в выплате
страхового возмещения или страховой суммы за последствия произошедших страховых
случаев.
Страховой взнос – плата за страхование, которую
страхователь обязан внести страховщику
по договору страхования или по закону. Размер страхового взноса исчисляется в
соответствии со страховым тарифом.
Расчет величины
ежегодного прироста (снижения) совокупного резерва взносов осуществляется
сальдовым методом. Формула имеет следующий вид:
Р = Д – В – У – Н – О - П, ( 1 )
где Р — годовой прирост резерва
взноса; Д — поступления страховых взносов и других доходов; В — фактические
выплаты страховых сумм в соответствии с договорами о наступлении страхового
случая; У — заложенная в тарифах сумма выплат в связи с наступлением страхового
случая. Она определяется как произведение установленного среднего тарифного
норматива на число сотен страховой суммы в соответствии с заключенным
договором; Н — заложенная в тарифах сумма расходов на содержание страховых
органов, которая исчисляется в установленном проценте от поступивших за год
взносов по различным видам страхования; О — остаток резерва взносов,
образующийся при выплатах выкупных сумм, поскольку размер выкупной суммы
несколько меньше накопившегося резерва на момент досрочного прекращения
договора с правом на выкуп. Он исчисляется в установленном проценте от
выплаченных выкупных сумм; П — прибыль от фактических выплат в связи с
наступлением страхового случая и расходов по ведению дела.
Основными источниками
финансирования страховых компаний являются:
- средства федерального и
местных бюджетов;
-средства
государственных и общественных организаций и
предприятий, других хозяйствующих субъектов;
- безвозмездные
(благотворительные) взносы и пожертвования;
- доходы от операций с
ценными бумагами;
- кредиты банков и других
финансовых небанковских учреждений;
- иные источники, не
запрещенные законодательством.
Страховой тариф- это цена страховой услуги, которая исчисляется на основании
актуарных расчетов. С помощью методов страховых финансовых вычислений и на базе
статистических расчетов частоты наступления страхового случая в связи с
основами теории определяется размер страхового тарифа для разных видов
страхования, на различных рыночных сегментах, в зависимости от ряда внешних и
внутренних факторов.
Страховые тарифы по
обязательным видам страхования устанавливаются в законах об обязательном
страховании. Страховые тарифы по добровольным видам личного страхования,
страхования имущества и ответственности могут устанавливаться страховщиками
самостоятельно и индивидуально — в зависимости от конкретного страхователя.
Страхователь вправе
уплачивать взносы сам или поручить оплату любому другому физическому или
юридическому лицу в рублях или иностранной валюте при согласии страховщика. Платежи
можно производить наличными деньгами страховому агенту (инспектору, брокеру),
через банк, почтовым переводом, а также с помощью различных форм безналичных
расчетов. Просрочка уплаты страховых взносов прекращает или изменяет условия
страховых обязательств либо дает право на принудительное взыскание страхового
взноса. При заключении договора страхователь обязан определить и сообщить все
необходимые сведения об обстоятельствах, составляющих страховой, а также
оговорить условия, превращающие его в страховой случай.
В результате деятельности
страхователя (полисодержателя) может наступить страховое событие- потенциальный страховой случай, на предмет
которого производится страхование. Выплаты по страховому событию осуществляются
при наступлении страхового случая-
наступившее событие, влекущее за собой нанесение материального или морального
ущерба юридическим и/или физическим лицам, которое обязывает страховщика
выплатить возмещение.
Страховой рынок и его
функционирование связанно с рисковой деятельностью субъектов. В результате
страхования организация несет страховой
риск- вероятность наступления страхового случая.
Если ставка возмещения
ущерба слишком велика или страховая сумма значительна, то страховая организация
может осуществить перестрахования и операцию ретроцессии.
Перестрахование – это система экономических отношений, в процессе которых
страховщик, принимая на страхование определенные риски, передает часть
ответственности по ним, с учетом своих финансовых возможностей, на
согласованных условиях другим страховщикам с целью создания сбалансированного
портфеля страхований, обеспечения собственной финансовой устойчивости и
рентабельности. Одновременно передается и соответствующая доля страховой
премии.
Ретроцессия – операция, при которой, приняв в перестрахование риск,
перестраховщик может частично передать его другому (третьему, четвертому)
страховщику(перестраховщику).
Защита личных и
общественных интересов, которые появляются в процессе производства, возможна
только при наличии страхования. Страхование в условиях рыночной экономики
просто необходимо.
1.3. Методы расчета тарифных ставок в рисковых видах
страхования
Страховая статистика на
уровне страховых компаний осуществляет тарифные расчеты и разработку тарифных
ставок. Размер тарифной ставки зависит от вероятности наступления страхового
случая.
Тарифная ставка- цена услуги, оказываемой страховщиком населению, т.е.
своеобразная цена страховой защиты. Для страховщика это ставка возмещения
ущерба, причиненного страховым случаем. Она состоит из нетто-ставки и страховой
надбавки.
На базе системы
математических и статистических закономерностей, вероятностных оценок
наступления страхового случая разрабатывается методология расчетов тарифов по
всем видам страхования, вычисление страховых резервов и т.д.
Страховой резерв- страховой фонд, который предназначен для обеспечения
страховой защиты страхователей по видам страхования (имущественное, личное и
социальное страхование).
Полная тарифная ставка
состоит из нетто-ставки (основной части тарифа, предназначенной для создания
фонда на выплату страхового возмещения, рисковая надбавка) и нагрузки к ней
(надбавки: расходы на ведение дела, расходы на предупредительные мероприятия,
прибыль).
Полная тарифная ставка
(брутто-ставка) находится по формуле:
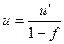 (2)
(2)
где f – рисковая надбавка к страховому
тарифу вводится для учета вероятного превышения ущерба относительно ожидаемого
значения, u’-
нетто-ставка, выражает рисковую часть тарифа для обеспечения страхового
возмещения. Предназначена для формирования страхового фонда (совокупности
страховых платежей). Вычисляется с определенной степенью вероятности. И
находится по формуле:
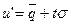 (3)
(3)
где 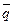 - средний уровень убыточности за период;
- средний уровень убыточности за период; 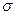 - среднее
квадратическое отклонение индивидуальных
уровней убыточности от среднего уровня; t – коэффициент доверительной
вероятности, определяемой по таблице на основании заданной вероятности.
- среднее
квадратическое отклонение индивидуальных
уровней убыточности от среднего уровня; t – коэффициент доверительной
вероятности, определяемой по таблице на основании заданной вероятности.
Среднее квадратическое
отклонение индивидуальных уровней убыточности от среднего уровня:
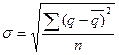 (4)
(4)
где q - убыточность страховой суммы.
Соотношение нетто-ставки
и надбавки регулируется индивидуально каждым страховщиком (на практике нагрузка
не превышает обычно 30% от брутто-ставки).
Для того, чтобы было лучше
понятно как рассчитываются эти показатели, рассмотрим пример:
Пример 1. Имеются данные о динамике
убыточности по страхованию имущества по организациям региона:
Таблица 1
|
Показатель
|
2002 г.
|
2003 г.
|
2004 г.
|
2005 г.
|
2006 г.
|
|
Убыточность
со 100 руб. страховой суммы, коп.
|
8
|
10
|
13
|
15
|
20
|
Нужно определить:
1) среднегодовой уровень убыточности;
2) нетто-ставку (с доверительной
вероятностью 0,954);
3) брутто-ставку, если известно, что
нагрузка по страхованию имущества составляет 12% к брутто-ставке.
Решение:
1) среднегодовой уровень убыточности
определяется по формуле :
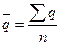 (5)
(5)
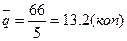
2) нетто-ставку исчисляется по
формуле (4)с учетом Р=0,954 ; t=2
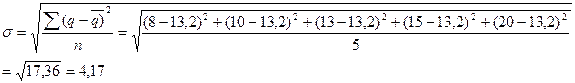
Следовательно, по формуле
(3) найдем нетто-ставку
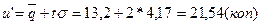
3) брутто-ставка
находится по формуле (2)
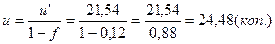
Дельта-надбавка
Для компенсации непредвиденных
обстоятельств к нетто-ставке рассчитывают гарантийную надбавку за риск,
называемую дельта-надбавкой, которая
находится по формуле:
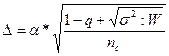 (6)
(6)
где 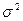 - дисперсия страховых выплат при наступлении страхового
случая:
- дисперсия страховых выплат при наступлении страхового
случая: 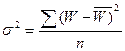 (7)
(7)
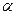 - коэффициент доверия, зависящий от вероятности безопасности.
- коэффициент доверия, зависящий от вероятности безопасности.
Абсолютные и относительные статистические показатели
страховой деятельности:
Страховое поле – максимально возможное количество объектов страхования (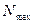 ).
).
Число страховых объектов(число заключенных договоров) – количество фактически застрахованных
объектов или заключенных страховщиком договоров (N).
Число страховых случаев – число наступивших страховых случаев (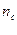 ).
).
Число пострадавших объектов – число пострадавших объектов в ходе наступления
страхового случая (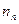 ).
).
Сумма поступивших платежей – сумма поступивших
платежей (V).
Сумма выплат возмещения - сумма выплат страхователю за потерю (ущерб)
имущества, жизни и т.п. по наступлении страхового случая (W).
Абсолютная сумма дохода страховых организаций – разница между суммой взносов и
выплат (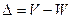 )
)
Страховая сумма
застрахованного имущества (S).
Сумма пострадавших
объектов (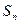 ).
).
Средние показатели
Средняя страховая сумма
застрахованного имущества
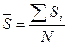 .
(8)
.
(8)
Средняя сумма страхового
платежей 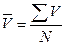 . (9)
. (9)
Средняя страховая сумма
пострадавших объектов
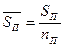 .
(10)
.
(10)
Средняя сумма страховых
выплат 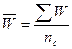 . (11)
. (11)
Относительные показатели
Уровень выплат страховых
сумм
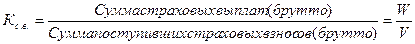 (12)
(12)
Степень охвата страхового
поля – рассчитывается как отношение количества заключенных договоров
страхования к страховому полю
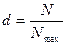 (13)
(13)
Частота страховых случаев
– показывает, сколько страховых случаев приходится на 100 застрахованных
объектов. Рассчитывается как отношение числа страховых случаев к количеству
застрахованных объектов
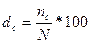 .
(14)
.
(14)
Коэффициент выплат
определяется по формуле:
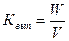 .
(15)
.
(15)
Убыточность страховой
суммы 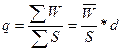 , (16)
, (16)
где 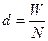 ,
, 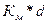 .
.
Средняя убыточность 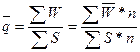 . (17)
. (17)
Коэффициент тяжести
страховых событий 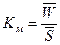 . (18)
. (18)
Абсолютный прирост
(снижение) уровня убыточности
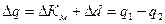 . (19)
. (19)
Абсолютный прирост за
счет отдельных факторов:
Уменьшения тяжести
страховых событий 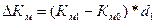 . (20)
. (20)
Изменения доли
пострадавших объектов 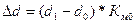 . (21)
. (21)
Индекс среднего уровня
убыточности переменного состава
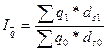 .
(22)
.
(22)
Индекс среднего уровня
убыточности постоянного состава
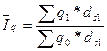 .
(23)
.
(23)
Индекс структурных
сдвигов 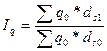 . (24)
. (24)
Взаимосвязь индексов 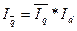 .
(25)
.
(25)
Индекс убыточности 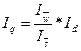 (26) или
(26) или
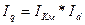 . (27)
. (27)
2. Расчетная часть
Вариант 20
Тема: Статистическое изучение страхового рынка
При проведении
статистического наблюдения за деятельностью страховых организаций одного из регионов РФ в отчетном году
получены выборочные данные об объеме доходов и прибыли по 30-ти страховым
компаниям (выборка 10%-ная, механическая).
В
проводимом статистическом исследовании эти страховые организации выступают как единицы
выборочной совокупности. Генеральную совокупность
образуют все страховые организации региона. Анализируемыми
признаками изучаемых единиц совокупности являются Доходы и Сумма
прибыли организаций.
Выборочные данные представлены в табл.1.
Таблица 1
Исходные
данные
|
№ организации,
п/п
|
доходы
|
прибыль
|
№
организации, п/п
|
доходы
|
прибыль
|
|
1
|
9,7
|
0,41
|
16
|
8,0
|
0,40
|
|
2
|
9,0
|
0,40
|
17
|
12,2
|
0,58
|
|
3
|
10,2
|
0,45
|
18
|
13,5
|
0,63
|
|
4
|
10,3
|
0,46
|
19
|
13,9
|
0,65
|
|
5
|
9,8
|
0,42
|
20
|
10,5
|
0,49
|
|
6
|
10,0
|
0,44
|
21
|
10,7
|
0,50
|
|
7
|
6,0
|
0,25
|
22
|
10,8
|
0,50
|
|
8
|
10,5
|
0,48
|
23
|
8,5
|
0,34
|
|
9
|
16,0
|
0,75
|
24
|
8,5
|
0,35
|
|
10
|
11,6
|
0,53
|
25
|
12,2
|
0,58
|
|
11
|
11,7
|
0,54
|
26
|
11,5
|
0,52
|
|
12
|
12,8
|
0,56
|
27
|
13,3
|
0,60
|
|
13
|
11,9
|
0,55
|
28
|
13,8
|
0,64
|
|
14
|
8,5
|
0,38
|
29
|
15,0
|
0,70
|
|
15
|
7,0
|
0,31
|
30
|
13,5
|
0,64
|
Задание 1
По исходным статистическим данным(табл.1) необходимо
выполнить следующее:
1. Построить статистический ряд
распределения организаций по доходам,
образовав пять групп с равным
интервалами.
2. Графическим методом и путем расчетов
определить значения моды и медианы полученного ряда распределения.
3.
Рассчитать характеристики ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации.
4.
Вычислить среднюю
арифметическую по исходным данным (табл. 1.1), сравнить её с аналогичным
показателем, рассчитанным в п. 3 для интервального ряда распределения.
Объяснить причину их расхождения.
Сделать выводы по результатам выполнения Задания 1.
Выполнение Задания 1
Целью выполнения
данного Задания
является изучение состава и структуры выборочной совокупности страховых
организаций путем построения и анализа статистического ряда распределения
страховых компаний по признаку Доходы.
1. Построение интервального ряда
распределения страховых организаций по доходам
Для построения
интервального вариационного ряда, характеризующего распределение страховых
организаций по доходам, необходимо вычислить величину и границы
интервалов ряда.
При построении ряда с
равными интервалами величина интервала h определяется по формуле
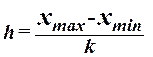 , (1)
, (1)
где 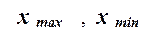 – наибольшее и наименьшее значения
признака в исследуемой совокупности, k- число групп интервального ряда.
– наибольшее и наименьшее значения
признака в исследуемой совокупности, k- число групп интервального ряда.
Число групп k задается в условии задания или рассчитывается
по формуле Г.Стерджесса
k=1+3,322 lg n, (2)
где n - число
единиц совокупности.
Определение
величины интервала по формуле (1) при заданных
k =
5, xmax = 16,0 млн руб., xmin = 6,0 млн руб.:
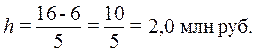
При h = 1.8 млн руб. границы
интервалов ряда распределения имеют следующий вид (табл. 2):
Таблица
2
|
Номер группы
|
Нижняя граница,
млн руб.
|
Верхняя граница,
млн руб.
|
|
1
|
6,0
|
8,0
|
|
2
|
8,0
|
10,0
|
|
3
|
10,0
|
12,0
|
|
4
|
12,0
|
14,0
|
|
5
|
14,0
|
16,0
|
Для
построения интервального ряда необходимо подсчитать число страховых
организаций, входящих в каждую группу (частоты групп). При этом возникает
вопрос, в какую группу включать единицы совокупности, у которых значения
признака выступают одновременно и верхней, и нижней границами смежных
интервалов (для демонстрационного примера – это 8,0; 10,0; 12,0; 14,0 млн
руб.). Отнесение таких единиц к одной из двух смежных групп рекомендуется
осуществлять по принципу полуоткрытого интервала [ ). Т.к. при этом верхние границы
интервалов не принадлежат данным интервалам, то соответствующие им единицы
совокупности включаются не в данную группу, а в следующую. В последний интервал
включаются и нижняя, и верхняя границы.
Процесс группировки
единиц совокупности по признаку Доход представлен во вспомогательной
(разработочной) таблице 3 (графа 4 этой таблицы необходима для построения
аналитической группировки в Задании 2).
Таблица 3
Разработочная таблица для построения интервального
ряда распределения и аналитической группировки
|
Группы страховых
организаций по доходам, млн руб.
|
Номер банка
|
Доход, млн руб.
|
Сумма прибыли,
млн руб.
|
|
1
|
2
|
3
|
4
|
|
6,0-8,0
|
7
|
6,0
|
0,25
|
|
15
|
7,0
|
0,31
|
|
Всего
|
2
|
13,0
|
0,56
|
|
8,0-10,0
|
1
|
9,7
|
0,41
|
|
2
|
9,0
|
0,40
|
|
5
|
9,8
|
0,42
|
|
14
|
8,5
|
0,38
|
|
16
|
8,0
|
0,40
|
|
23
|
8,5
|
0,34
|
|
24
|
8,5
|
0,35
|
|
Всего
|
7
|
62,0
|
2,7
|
|
10,0-12,0
|
3
|
10,2
|
0,45
|
|
4
|
10,3
|
0,46
|
|
6
|
10,0
|
0,44
|
|
8
|
10,5
|
0,48
|
|
10
|
11,6
|
0,53
|
|
11
|
11,7
|
0,54
|
|
13
|
11,9
|
0,55
|
|
20
|
10,5
|
0,49
|
|
21
|
10,7
|
0,50
|
|
22
|
10,8
|
0,50
|
|
26
|
11,5
|
0,52
|
|
Всего
|
11
|
119,7
|
5,46
|
|
12,0-14,0
|
12
|
12,8
|
0,56
|
|
17
|
12,2
|
0,58
|
|
18
|
13,5
|
0,63
|
|
19
|
13,9
|
0,65
|
|
25
|
12,2
|
0,58
|
|
27
|
13,3
|
0,60
|
|
28
|
13,8
|
0,64
|
|
30
|
13,5
|
0,64
|
|
Всего
|
8
|
105,2
|
4,88
|
|
14,0-16,0
|
9
|
16,0
|
0,75
|
|
29
|
15,0
|
0,70
|
|
Всего
|
2
|
31,0
|
1,23
|
|
ИТОГО
|
30
|
330,9
|
15,05
|
На основе групповых
итоговых строк «Всего» табл. 3 формируется итоговая таблица 4, представляющая интервальный
ряд распределения страховых организаций по доходу.
Таблица 4
Распределение страховых организаций по доходу
|
Номер группы
|
Группы страх.организаций по доходу, млн
руб.,
х
|
Число страх. организаций,
f
|
|
1
|
6,0-8,0
|
2
|
|
2
|
8,0-10,0
|
7
|
|
3
|
10,0-12,0
|
11
|
|
4
|
12,0-14,0
|
8
|
|
5
|
14,0-16,0
|
2
|
|
Итого
|
30
|
Помимо частот
групп в абсолютном выражении в анализе интервальных рядов используются ещё три
характеристики ряда, приведенные в графах 4 - 6 табл. 1.4. Это частоты групп в относительном выражении,
накопленные (кумулятивные) частоты Sj, получаемые путем последовательного
суммирования частот всех предшествующих (j-1) интервалов, и накопленные
частости, рассчитываемые по формуле 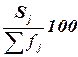 .
.
Таблица 5
Структура страх.организаций по доходу
|
№ группы
|
Группы страх.организаций подоходу, млн руб.
|
Число страх.организаций, fj
|
Накопленная
частота,
Sj
|
Накопленная
частоcть, %
|
|
в абсолютном выражении
|
в % к итогу
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
6,0-8,0
|
2
|
6,7
|
2
|
6,7
|
|
2
|
8,0-10,0
|
7
|
23,3
|
9
|
30,0
|
|
3
|
10,0-12,0
|
11
|
36,7
|
20
|
66,7
|
|
4
|
12,0-14,0
|
8
|
26,7
|
28
|
93,3
|
|
5
|
14,0-16,0
|
2
|
6,7
|
30
|
100,0
|
|
Итого
|
30
|
100,0
|
|
|
Вывод. Анализ интервального ряда распределения
изучаемой совокупности страховых организаций показывает, что распределение страховых
организаций по доходу не является равномерным: преобладают страховые
организации с доходами от 10 млн руб. до 12 млн руб. (это 11 страховых
организаций, доля которых составляет 36,7%); 30% страховых организаций имеют доход
менее 10 млн руб., а 93,3% – менее 14 млн руб.
2.
Нахождение моды и медианы полученного интервального ряда распределения
графическим методом и путем расчетов
Для определения моды графическим методом строим по данным табл. 4
(графы 2 и 3) гистограмму распределения страховых организаций по изучаемому
признаку.

Рис. 1. Определение
моды графическим методом
Расчет конкретного значения моды для
интервального ряда распределения производится по формуле:
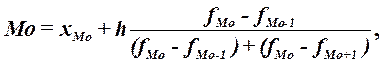 (3)
(3)
где
хМo – нижняя граница модального
интервала,
h – величина модального интервала,
fMo – частота модального интервала,
fMo-1 – частота интервала, предшествующего модальному,
fMo+1 –
частота интервала, следующего за модальным.
Согласно табл. 4
модальным интервалом построенного ряда является интервал 10 - 12 млн.руб., т.к.
он имеет наибольшую частоту (f3=11). Расчет моды по формуле (3):
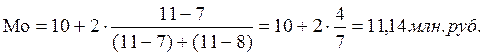
Вывод. Для рассматриваемой совокупности
страховых организаций наиболее распространенный доход характеризуется средней
величиной 11,14 млн.руб.
Для определения медианы графическим методом строим по данным табл.
5 (графы 2 и 5) кумуляту распределения страховых организаций по признаку- доход.
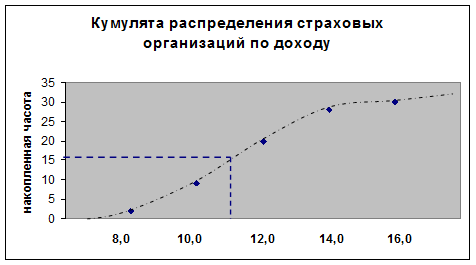
Рис. 2. Определение медианы
графическим методом
Расчет конкретного значения медианы для интервального ряда
распределения производится по формуле
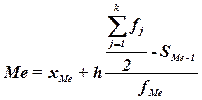 ,
(4)
,
(4)
где
хМе– нижняя граница медианного интервала,
h – величина медианного интервала,
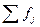 – сумма всех частот,
– сумма всех частот,
fМе – частота медианного интервала,
SMе-1 – кумулятивная (накопленная) частота
интервала, предшествующего медианному.
Определяем медианный
интервал, используя графу 5 табл. 5. Медианным интервалом является интервал
10-12 млн.руб., т.к. именно в этом интервале накопленная частота Sj=20 впервые превышает полусумму всех частот (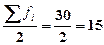 ).
).
Расчет медианы по формуле
(4):
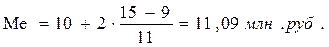
Вывод. В рассматриваемой совокупности
организаций половина страховых компаний имеют средний доход не более 11,09
млн.руб, а другая половина – не менее 11,09 млн.руб.
3. Расчет
характеристик ряда распределения
Для расчета характеристик ряда распределения 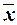 , σ, σ2, Vσ на основе табл. 5 строим
вспомогательную таблицу 6 (
, σ, σ2, Vσ на основе табл. 5 строим
вспомогательную таблицу 6 (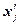 – середина интервала).
– середина интервала).
|
|
|
|
|
|
таблица
6
|
|
Расчетная таблица для нахождения характеристик ряда
распределения
|
|
Группы страх.организаций по доходу, млн.руб
|
Середина
интервала,xi
|
Число фирм,fj
|
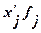
|
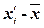
|
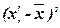
|
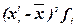
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
6,0-8,0
|
7,0
|
2
|
14
|
-4,067
|
16,5378
|
33,0756
|
|
8,0-10,0
|
9,0
|
7
|
63
|
-2,067
|
4,2711
|
29,8978
|
|
10,0-12,0
|
11,0
|
11
|
121
|
-0,067
|
0,0044
|
0,0489
|
|
12,0-14,0
|
13,0
|
8
|
104
|
1,933
|
3,7378
|
29,9022
|
|
14,0-16,0
|
15,0
|
2
|
30
|
3,933
|
15,4711
|
30,9422
|
|
Итого
|
|
30
|
332
|
|
|
123,8667
|
Рассчитаем среднюю арифметическую
взвешенную:
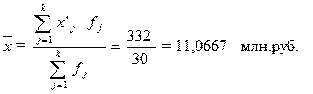 (5)
(5)
Рассчитаем среднее квадратическое
отклонение:
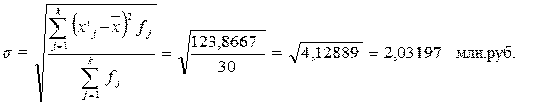 (6)
(6)
Рассчитаем дисперсию:
σ2 = 4,12889
млн.руб.
Рассчитаем коэффициент вариации:
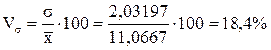 (7)
(7)
Вывод. Анализ полученных значений
показателей 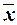 и σ говорит о том, что
средняя величина доходов составляет 11,07 млн.руб., отклонение от этой величины
в ту или иную сторону составляет в среднем 2,03 млн.руб. (или 18,4%), наиболее
характерный средний доход находится в пределах от 9,04 до 13,1 млн.руб. (диапазон
и σ говорит о том, что
средняя величина доходов составляет 11,07 млн.руб., отклонение от этой величины
в ту или иную сторону составляет в среднем 2,03 млн.руб. (или 18,4%), наиболее
характерный средний доход находится в пределах от 9,04 до 13,1 млн.руб. (диапазон 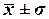 ).
).
Значение Vσ = 18,4% не превышает 33%,
следовательно, вариация среднего дохода в исследуемой совокупности страховых
организаций незначительна и совокупность по данному признаку однородна.
Расхождение между значениями 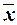 , Мо и Ме незначительно (
, Мо и Ме незначительно (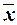 = 11,07млн.руб., Мо=11,14млн.руб.,
Ме= 11,09млн.руб.), что подтверждает
вывод об однородности совокупности страховых организаций. Таким образом,
найденное среднее значение средних доходов (11,07 млн.руб.) является типичной,
надежной характеристикой исследуемой совокупности страховых компаний.
= 11,07млн.руб., Мо=11,14млн.руб.,
Ме= 11,09млн.руб.), что подтверждает
вывод об однородности совокупности страховых организаций. Таким образом,
найденное среднее значение средних доходов (11,07 млн.руб.) является типичной,
надежной характеристикой исследуемой совокупности страховых компаний.
4. Вычисление средней арифметической по
исходным данным о среднестатистическим
доходам страховых компаний
Для расчета применяется формула средней арифметической
простой:
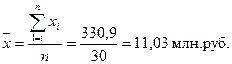 , (8)
, (8)
Причина расхождения
средних величин, рассчитанных по исходным данным (11,03 млн.руб.) и по интервальному
ряду распределения (11,07 млн.руб.), заключается в том, что в первом случае
средняя определяется по фактическим значениям исследуемого признака для
всех 30-ти фирм, а во втором случае в качестве значений признака берутся середины
интервалов 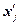 и, следовательно, значение средней будет менее
точным. Вместе с тем, при округлении обеих рассматриваемых величин их значения
совпадают (11млн.руб.), что говорит о достаточно равномерном распределении
дохода внутри каждой группы интервального ряда.
и, следовательно, значение средней будет менее
точным. Вместе с тем, при округлении обеих рассматриваемых величин их значения
совпадают (11млн.руб.), что говорит о достаточно равномерном распределении
дохода внутри каждой группы интервального ряда.
Задание 2
По исходным
данным (табл. 1) с использованием
результатов выполнения Задания 1 необходимо выполнить следующее:
1.
Установить наличие и характер корреляционной связи между
признаками доходы и прибыль, образовав пять групп с равными интервалами по каждому
из признаков, используя методы:
а) аналитической
группировки;
б)
корреляционной таблицы.
2. Измерить
тесноту корреляционной связи, используя коэффициент
детерминации и эмпирическое корреляционное отношение.
Сделать
выводы по результатам выполнения задания 2.
Выполнение задания 2
Целью
выполнения данного задания
является выявление наличия корреляционной связи между факторным и
результативным признаками, а также установление направления связи и оценка ее
тесноты.
По условию
Задания 2 факторным является признак доход, результативным – прибыль.
1. Установление наличия и характера
корреляционной связи между признаками Доход и Прибыль методами аналитической группировки и корреляционных таблиц
1а. Применение метода аналитической группировки
Аналитическая группировка строится
по факторному признаку Х и для
каждой j-ой группы ряда
определяется среднегрупповое значение 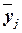 результативного признака Y. Если с
ростом значений фактора Х от группы
к группе средние значения
результативного признака Y. Если с
ростом значений фактора Х от группы
к группе средние значения 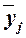 систематически
возрастают (или убывают), между признаками X и Y имеет
место корреляционная связь.
систематически
возрастают (или убывают), между признаками X и Y имеет
место корреляционная связь.
Используя разработочную таблицу 3, строим аналитическую группировку,
характеризующую зависимость между факторным признаком Х- Доход и результативным признаком Y - Прибыль.
Макет аналитической таблицы имеет следующий вид (табл. 7):
Таблица 7
Зависимость прибыли от средней
величины доходов
|
Номер группы
|
Группы
страх.организаций по средней величине доходов, млн.руб.
x
|
Число организаций,
fj
|
Прибыль, млн руб.
|
|
всего
|
в среднем на одну
организацию,
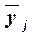
|
|
1
|
2
|
3
|
4
|
5=4:3
|
|
1
|
|
|
|
|
|
2
|
|
|
|
|
|
3
|
|
|
|
|
|
4
|
|
|
|
|
|
5
|
|
|
|
|
|
ИТОГО
|
|
|
|
Групповые средние значения 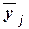 получаем из
таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную
аналитическую группировку представляет табл. 8:
получаем из
таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную
аналитическую группировку представляет табл. 8:
Таблица 8
Зависимость Прибыли от средней
величины доходов
|
Номер группы
|
Группы
страх.организаций по средней величине доходов, млн.руб. x
|
Число
организаций, fj
|
Прибыль, млн руб.
|
|
|
всего
|
в среднем на одну
организацию, ỹi
|
|
|
|
1
|
2
|
3
|
4
|
5=4:3
|
|
|
1
|
6,0-8,0
|
2
|
0,56
|
0,28
|
|
|
2
|
8,0-10,0
|
7
|
2,7
|
0,39
|
|
|
3
|
10,0-12,0
|
11
|
5,46
|
0,50
|
|
|
4
|
12,0-14,0
|
8
|
4,88
|
0,61
|
|
|
5
|
14,0-16,0
|
2
|
1,45
|
0,73
|
|
|
|
ИТОГО
|
30,0
|
15,05
|
2,50
|
|
Вывод. Анализ данных табл. 8 показывает, что с увеличением
средней величины доходов от группы к группе систематически возрастает и средний
объем прибыли по каждой группе организаций, что свидетельствует о наличии
прямой корреляционной связи между исследуемыми признаками.
1.б. Применение метода корреляционных
таблиц
Корреляционная
таблица строится как комбинация двух рядов распределения по факторному признаку
Х и результативному признаку Y. На
пересечении j-ой строки
и k-ой графы
таблицы указывается число единиц совокупности, входящих в j-ый интервал по признаку X и в k-ый
интервал по признаку Y.
Концентрация частот около диагонали построенной таблицы свидетельствует о
наличии корреляционной связи между признаками - прямой или обратной. Связь
прямая, если частоты располагаются по диагонали, идущей от левого верхнего угла
к правому нижнему, обратная - по диагонали от правого верхнего угла к левому
нижнему.
Для
построения корреляционной таблицы необходимо знать величины и границы
интервалов по двум признакам X и Y. Для
факторного признака Х – доход, эти величины известны из табл. 4 Определяем величину интервала для
результативного признака Y – Прибыль при k = 5, уmax = 0,75 млн руб., уmin = 0,25 млн руб.:
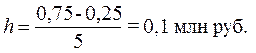
Границы интервалов ряда распределения
результативного признака Y имеют вид:
Таблица 9
|
Номер группы
|
Нижняя
граница, млн.руб.
|
Верхняя
граница, млн.руб.
|
|
1
|
0,25
|
0,35
|
|
2
|
0,35
|
0,45
|
|
3
|
0,45
|
0,55
|
|
4
|
0,55
|
0,65
|
|
5
|
0,65
|
0,75
|
Подсчитывая для каждой группы число входящих в нее фирм с
использованием принципа полуоткрытого интервала [ ), получаем интервальный
ряд распределения результативного признака (табл. 10).
Таблица 10
Интервальный ряд
распределения организаций по прибыли
|
Группы страховых организаций по прибыли,
млн руб.,
у
|
Число фирм,
fj
|
|
2,50-2,75
|
3
|
|
2,75-3,00
|
4
|
|
3,00-3,25
|
5
|
|
3,25-3,50
|
8
|
|
3,50-3,75
|
6
|
|
3,75-4,00
|
4
|
|
ИТОГО
|
30
|
Используя группировки по факторному и результативному
признакам, строим корреляционную таблицу (табл. 11).
Таблица
11
Корреляционная таблица зависимости объема продаж
от среднесписочной
численности менеджеров
|
группы организаций
средней величине по дохода, млн.руб.
|
группы
страх.организаций по прибыли,млн.руб
|
Итого
|
|
0,25-0,35
|
0,35-0,45
|
0,45-0,55
|
0,55-0,65
|
0,65-0,75
|
|
6,0-8,0
|
2
|
|
|
|
|
2
|
|
8,0-10,0
|
1
|
6
|
|
|
|
7
|
|
10,0-12,0
|
|
1
|
9
|
1
|
|
11
|
|
12,0-14,0
|
|
|
|
7
|
1
|
8
|
|
14,0-16,0
|
|
|
|
|
2
|
2
|
|
итого
|
3
|
7
|
9
|
8
|
3
|
30
|
Вывод. Анализ
данных табл. 11 показывает, что распределение частот групп произошло вдоль
диагонали, идущей из левого верхнего угла в правый нижний угол таблицы. Это
свидетельствует о наличии прямой корреляционной связи между средней суммой
доходов и прибыли.
2. Измерение тесноты корреляционной связи с использованием коэффициента
детерминации 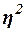 и эмпирического корреляционного отношения
и эмпирического корреляционного отношения 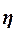
Коэффициент детерминации 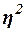 характеризует
силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля
межгрупповой дисперсии
характеризует
силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля
межгрупповой дисперсии 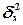 признака Y в его
общей дисперсии
признака Y в его
общей дисперсии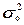 :
:
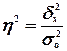 (9)
(9)
где 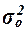 – общая дисперсия
признака Y,
– общая дисперсия
признака Y,
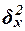 – межгрупповая
(факторная) дисперсия признака Y.
– межгрупповая
(факторная) дисперсия признака Y.
Общая
дисперсия 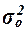 характеризует
вариацию результативного признака, сложившуюся под влиянием всех
действующих на Y факторов (систематических
и случайных) и вычисляется по формуле
характеризует
вариацию результативного признака, сложившуюся под влиянием всех
действующих на Y факторов (систематических
и случайных) и вычисляется по формуле
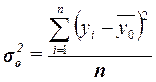 ,
(10)
,
(10)
где yi – индивидуальные значения
результативного признака;
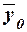 – общая средняя значений
результативного признака;
– общая средняя значений
результативного признака;
n – число единиц совокупности.
Межгрупповая дисперсия 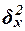 измеряет систематическую вариацию результативного признака,
обусловленную влиянием признака-фактора Х (по которому произведена группировка) и вычисляется по формуле
измеряет систематическую вариацию результативного признака,
обусловленную влиянием признака-фактора Х (по которому произведена группировка) и вычисляется по формуле
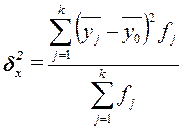 , (11)
, (11)
где 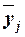 –групповые
средние,
–групповые
средние,
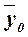 –
общая средняя,
–
общая средняя,
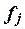 –число единиц в j-ой
группе,
–число единиц в j-ой
группе,
k – число групп.
Для расчета показателей 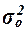 и
и 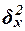 необходимо знать
величину общей средней
необходимо знать
величину общей средней 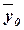 , которая
вычисляется как средняя арифметическая простая по всем единицам совокупности:
, которая
вычисляется как средняя арифметическая простая по всем единицам совокупности:
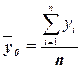 (12)
(12)
Значения числителя и знаменателя формулы имеются
в табл. 8 (графы 3 и 4 итоговой строки). Используя эти данные, получаем общую
среднюю 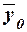 по формуле (12):
по формуле (12):
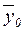 =
=
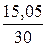 = 0,502 млн руб.
= 0,502 млн руб.
Для
расчета общей дисперсии 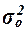 применяется вспомогательная таблица
12.
применяется вспомогательная таблица
12.
Таблица 12
Вспомогательная таблица для расчета общей дисперсии
|
номер организации
п/п
|
Прибыль, млн.руб.
|
Yi -Ỹo
|


|
|
|
1
|
0,41
|
-0,092
|
0,008
|
0,1681
|
|
2
|
0,40
|
-0,102
|
0,010
|
0,16
|
|
3
|
0,45
|
-0,052
|
0,003
|
0,2025
|
|
4
|
0,46
|
-0,042
|
0,002
|
0,2116
|
|
5
|
0,42
|
-0,082
|
0,007
|
0,1764
|
|
6
|
0,44
|
-0,062
|
0,004
|
0,1936
|
|
7
|
0,25
|
-0,252
|
0,063
|
0,0625
|
|
8
|
0,48
|
-0,022
|
0,000
|
0,2304
|
|
9
|
0,75
|
0,248
|
0,062
|
0,5625
|
|
10
|
0,53
|
0,028
|
0,001
|
0,2809
|
|
11
|
0,54
|
0,038
|
0,001
|
0,2916
|
|
12
|
0,56
|
0,058
|
0,003
|
0,3136
|
|
13
|
0,55
|
0,048
|
0,002
|
0,3025
|
|
14
|
0,38
|
-0,122
|
0,015
|
0,1444
|
|
15
|
0,31
|
-0,192
|
0,037
|
0,0961
|
|
16
|
0,40
|
-0,102
|
0,010
|
0,16
|
|
17
|
0,58
|
0,078
|
0,006
|
0,3364
|
|
18
|
0,63
|
0,128
|
0,016
|
0,3969
|
|
19
|
0,65
|
0,148
|
0,022
|
0,4225
|
|
20
|
0,49
|
-0,012
|
0,000
|
0,2401
|
|
21
|
0,50
|
-0,002
|
0,000
|
0,25
|
|
22
|
0,50
|
-0,002
|
0,000
|
0,25
|
|
23
|
0,34
|
-0,162
|
0,026
|
0,1156
|
|
24
|
0,35
|
-0,152
|
0,023
|
0,1225
|
|
25
|
0,58
|
0,078
|
0,006
|
0,3364
|
|
26
|
0,52
|
0,018
|
0,000
|
0,2704
|
|
27
|
0,60
|
0,098
|
0,010
|
0,36
|
|
28
|
0,64
|
0,138
|
0,019
|
0,4096
|
|
29
|
0,70
|
0,198
|
0,039
|
0,49
|
|
30
|
0,64
|
0,138
|
0,019
|
0,4096
|
|
итого
|
15,05
|
-0,001
|
0,417
|
7,9667
|
Рассчитаем общую
дисперсию по формуле (10):
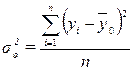 =
=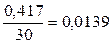
Для расчета межгрупповой дисперсии 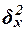 строится вспомогательная таблица 13, при этом
используются групповые средние значения
строится вспомогательная таблица 13, при этом
используются групповые средние значения 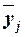 из табл. 8 (графа 5).
из табл. 8 (графа 5).
Таблица 13
Вспомогательная таблица для расчета межгрупповой
дисперсии
|
Группы
страх.организаций по средней величине доходов,млн.руб., х
|
Число организаций,
Fj
|
среднее значение в
группе, млн.руб.
|


|
|
|
6,0-8,0
|
2
|
0,28
|
-0,222
|
0,098272
|
|
8,0-10,0
|
7
|
0,39
|
-0,116
|
0,094115
|
|
10,0-12,0
|
11
|
0,50
|
-0,005
|
0,000309
|
|
12,0-14,0
|
8
|
0,61
|
0,108
|
0,093889
|
|
14,0-16,0
|
2
|
0,73
|
0,223
|
0,099756
|
|
Итого
|
|
|
|
0,386341
|
Рассчитаем межгрупповую дисперсию
по формуле (11):
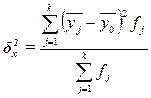
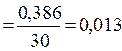
Определяем
коэффициент детерминации по формуле (9):
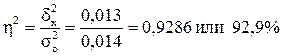
Вывод. 92,9% вариации прибыли страховой
компанией обусловлено вариацией средней величины дохода, а 7,1% – влиянием
прочих неучтенных факторов.
Эмпирическое корреляционное отношение 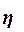 оценивает тесноту
связи между факторным и результативным признаками и вычисляется по
формуле
оценивает тесноту
связи между факторным и результативным признаками и вычисляется по
формуле
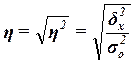 (13)
(13)
Рассчитаем
показатель 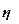 по формуле (13):
по формуле (13):
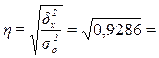 0,96
0,96
Чем ближе значение 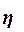 к 1, тем теснее связь между признаками. Для
качественной оценки тесноты связи на основе
к 1, тем теснее связь между признаками. Для
качественной оценки тесноты связи на основе 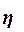 служит шкала Чэддока (табл. 14):
служит шкала Чэддока (табл. 14):
Таблица
14
Шкала Чэддока
|
h
|
0,1 – 0,3
|
0,3 – 0,5
|
0,5 – 0,7
|
0,7 – 0,9
|
0,9 – 0,99
|
|
Характеристика
силы связи
|
Слабая
|
Умеренная
|
Заметная
|
Тесная
|
Весьма тесная
|
Вывод: согласно
шкале Чэддока связь между средней величиной доходов и прибылью является весьма
тесной.
Задание 3
По
результатам выполнения Задания 1 с вероятностью 0,954 необходимо определить:
1)
ошибку выборки для средней величины доходов и границы в которых она находится в генеральной
совокупности.
2)
ошибку выборки
доли страховых организаций с доходами 14 млн.руб. и более и границы, в которых
будет находиться генеральная доля.
Выполнение Задания 3
Целью выполнения данного
Задания является
определение для генеральной совокупности страховых организаций границ, в
которых будут находиться средняя величина доходов, и доля страховых организаций с
доходами 14 млн.руб. и более.
1.
Определение ошибки выборки для средней
величины доходов, а также границ, в которых будет находиться генеральная
средняя
Применяя
выборочный метод наблюдения, необходимо рассчитать ошибки выборки (ошибки
репрезентативности), т.к. генеральные и выборочные характеристики, как правило,
не совпадают, а отклоняются на некоторую величину ε.
Принято вычислять два вида
ошибок выборки - среднюю 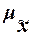 и предельную
и предельную 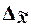 .
.
Для расчета средней ошибки выборки 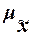 применяются различные формулы в зависимости от вида и способа отбора единиц
из генеральной совокупности в выборочную.
применяются различные формулы в зависимости от вида и способа отбора единиц
из генеральной совокупности в выборочную.
Для собственно-случайной
и механической выборки с бесповторным способом отбора средняя ошибка 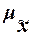 для выборочной средней
для выборочной средней 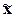 определяется по
формуле
определяется по
формуле
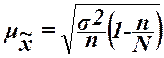 ,
(15)
,
(15)
где 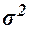 – общая дисперсия изучаемого признака,
– общая дисперсия изучаемого признака,
N – число единиц в генеральной совокупности,
n – число единиц в выборочной совокупности.
Предельная ошибка выборки 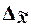 определяет границы, в пределах
которых будет находиться генеральная средняя:
определяет границы, в пределах
которых будет находиться генеральная средняя:
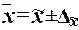 ,
,
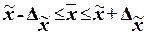 ,
(16)
,
(16)
где 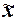 – выборочная средняя,
– выборочная средняя,
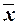 – генеральная средняя.
– генеральная средняя.
Предельная
ошибка выборки 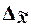 кратна средней ошибке
кратна средней ошибке 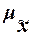 с коэффициентом кратности t (называемым также коэффициентом доверия):
с коэффициентом кратности t (называемым также коэффициентом доверия):
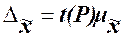 (17)
(17)
Коэффициент
кратности t зависит от
значения доверительной вероятности
Р, гарантирующей вхождение генеральной средней в интервал 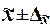 , называемый доверительным интервалом.
, называемый доверительным интервалом.
Наиболее
часто используемые доверительные вероятности Р и соответствующие им
значения t задаются следующим образом (табл. 14):
Таблица 15
|
Доверительная вероятность P
|
0,683
|
0,866
|
0,954
|
0,988
|
0,997
|
0,999
|
|
Значение t
|
1,0
|
1,5
|
2,0
|
2,5
|
3,0
|
3,5
|
По условию Задания 2 выборочная совокупность насчитывает 30
страховых организаций, выборка 10% механическая, следовательно, генеральная
совокупность включает 300 фирм. Выборочная средняя 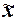 , дисперсия
, дисперсия 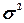 определены
в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи,
представлены в табл. 15:
определены
в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи,
представлены в табл. 15:
Таблица 16
|
Р
|
t
|
n
|
N
|
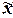
|
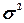
|
|
0,954
|
2
|
30
|
300
|
11,067
|
4,129
|
Рассчитаем среднюю ошибку выборки по формуле (15):
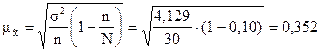 млн.руб.
млн.руб.
Рассчитаем
предельную ошибку выборки:
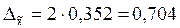 млн.руб.
млн.руб.
Определим
доверительный интервал для генеральной средней:
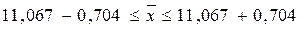
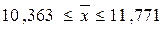
Вывод. На основании проведенного
выборочного обследования с вероятностью 0,954 можно утверждать, что для
генеральной совокупности страховых компаний средняя величина доходов находится
в пределах от 10,36 до 11,77 млн.руб.
2. Определение
ошибки выборки доли страховых организаций с доходами 14 млн.руб. и более, а
также границ, в которых будет находиться генеральная доля
Доля
единиц выборочной совокупности, обладающих тем или иным заданным свойством,
выражается формулой
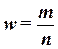 ,
(18)
,
(18)
где m – число
единиц совокупности, обладающих заданным свойством;
n – общее число единиц в совокупности.
Для собственно-случайной
и механической выборки с бесповторным способом отбора предельная
ошибка выборки 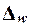 доли единиц,
обладающих заданным свойством, рассчитывается по формуле
доли единиц,
обладающих заданным свойством, рассчитывается по формуле
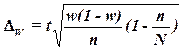 , (19)
, (19)
где
w – доля
единиц совокупности, обладающих заданным свойством;
(1-w) – доля единиц совокупности, не обладающих заданным свойством,
N – число единиц в генеральной
совокупности,
n– число единиц в выборочной
совокупности.
Предельная ошибка выборки 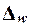 определяет границы, в пределах
которых будет находиться генеральная доля р единиц, обладающих исследуемым признаком:
определяет границы, в пределах
которых будет находиться генеральная доля р единиц, обладающих исследуемым признаком:
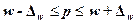
По
условию Задания 3 исследуемым свойством страховых организаций является равенство
или превышение средней величины доходов 14 млн.руб..
Число
страховых организаций с данным свойством определяется из табл. 3 (графа 3):
m=2
Рассчитаем
выборочную долю:
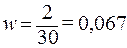
Рассчитаем
предельную ошибку выборки для доли:
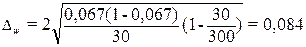
Определим
доверительный интервал генеральной доли:
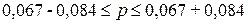
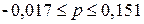
или
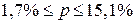
Вывод. С вероятностью
0,954 можно утверждать, что в генеральной совокупности доля страховых
организаций с доходами 14 млн.руб. и более будет находиться в пределах от 1,7%
до 15,1%.
Задание 4
Определите тарифную ставку страхования профессиональной ответственности
аудиторов при средней убыточности 55 руб. на 100 руб. страховых сумм,
экспертной оценке вероятности наступления страхового события – 0,05, числе
договоров – 1200, доле абсолютной нагрузки в брутто-ставке – 25% и вероятности
непревышения возмещения по сравнению со страховыми суммами – 0,997.
Выполнение Задания 4
Полная тарифная ставка находится по формуле:
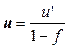 ,
(20)
,
(20)
где u’-
нетто-ставка, f-
надбавка к страховому тарифу.
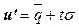 ,
(21)
,
(21)
где 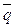 - средний уровень убыточности за период, t- коэффициент доверительной вероятности,
определяемой по таблице, σ-
среднее квадратичное отклонение, t – коэффициент доверительной
вероятности.
- средний уровень убыточности за период, t- коэффициент доверительной вероятности,
определяемой по таблице, σ-
среднее квадратичное отклонение, t – коэффициент доверительной
вероятности.
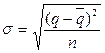 (22)
(22)
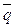 = 55, q= 100, t=3 ( по P=0,997), n= 30
= 55, q= 100, t=3 ( по P=0,997), n= 30
По формуле (22) рассчитаем средне квадратичное отклонение
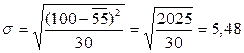
По формуле (21) рассчитаем нетто-ставку
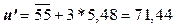
По формуле (20) рассчитаем тарифную ставку
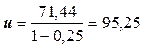 .
.
Вывод: Тарифная ставка страхования профессиональной ответственности
аудиторов будет составлять 95,25 руб. от 100руб. страховых сумм.
3. Аналитическая часть
3.1. Постановка задачи
По данным отчетов сборов страховых премий за несколько лет,
представленным в таблице 1, проведем анализ динамики страховых премий, для чего
рассчитаем следующие показатели: абсолютный прирост; темп роста; абсолютное
значение 1% прироста; средние за период уровень ряда, абсолютный прирост, темпы
роста и прироста.
Таблица 1
Сборы страховых премий за 2000-2006 г., всего по рынку.
|
Год
|
Страховые премии, млрд.руб.
|
|
2000
|
171
|
|
2001
|
276,6
|
|
2002
|
300,4
|
|
2003
|
432,5
|
|
2004
|
471,6
|
|
2005
|
490,6
|
|
2006
|
602,1
|
3.2. Методика решения задачи
Расчет показателей анализа ряда динамики осуществим по формулам,
представленным в таблице 2.
Таблица 2
|
Показатель
|
Базисный
|
Цепной
|
Средний
|
|
Абсолютный прирост
|
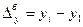 (1) (1)
|
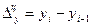 (2) (2)
|
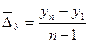 (3) (3)
|
|
Темп роста
|
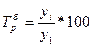 (4) (4)
|
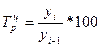 (5) (5)
|
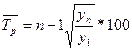 (6) (6)
|
|
Темп прироста
|
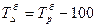 (7) (7)
|
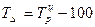 (8) (8)
|
 (9) (9)
|
Средний уровень в интервальном ряду
динамики вычисляется по формуле:
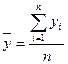 (10)
(10)
Для определения абсолютной величины, стоящей за каждым процентом прироста
страховой премии, рассчитывают показатель абсолютного значения 1% прироста
(А%). Один из способов его расчета – расчет по формуле: 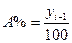 (11)
(11)
Числовые обозначения:
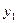 - уровень
первого периода,
- уровень
первого периода, 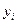 - уровень
сравниваемого периода,
- уровень
сравниваемого периода, 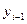 - уровень предыдущего
периода,
- уровень предыдущего
периода, 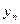 - уровень последнего
периода, n – число
уровней ряда динамики.
- уровень последнего
периода, n – число
уровней ряда динамики.
3.3. Технологические расчеты
Расчеты показателей анализа динамики страховых премий выполнены с
применением пакета прикладных программ обработки электронных таблиц MS Excel.
Все данные и расчетные формулы представлены в таблице 3.
Таблица 3
|
Сборы страховых
премий за 2000-2006 года, всего по рынку
|
|
год
|
сумма премий,
млрд.руб.
|
Абсолютный
прирост,млрд.руб.базисный
|
Абсолютный
прирост,млрд.руб.цепной
|
темп роста,%
базисный
|
темп роста,% цепной
|
темп прироста,%
базисный
|
темп прироста,%
цепной
|
абсолютное значение
одного прицента прироста А%,млрд.руб
|
|
2000
|
171
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
2001
|
276,6
|
105,6
|
105,6
|
161,75439
|
161,7544
|
61,75439
|
61,75439
|
1,71
|
|
2002
|
300,4
|
129,4
|
23,8
|
175,67251
|
108,6045
|
75,67251
|
8,604483
|
2,766
|
|
2003
|
432,5
|
261,5
|
132,1
|
252,92398
|
143,9747
|
152,924
|
43,9747
|
3,004
|
|
2004
|
471,6
|
300,6
|
39,1
|
275,78947
|
109,0405
|
175,7895
|
9,040462
|
4,325
|
|
2005
|
490,6
|
319,6
|
19
|
286,90058
|
104,0288
|
186,9006
|
4,028838
|
4,716
|
|
2006
|
602,1
|
431,1
|
111,5
|
352,10526
|
122,7273
|
252,1053
|
22,72727
|
4,906
|
|
итого
|
2744,8
|
|
|
|
|
|
|
|
|
средний уровень
ряда
|
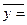
|
392,11429
|
|
|
|
|
|
средний абсолютный
прирост
|
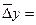
|
71,85
|
|
|
|
|
|
средний темп роста
|
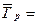
|
136,98346
|
|
|
|
|
|
средний темп
прироста
|
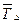 = =
|
36,983459
|
|
|
|
|
3.4. Выводы
Сумма страховых премий за 7 лет выросло на 252,1% что абсолютное
выражение составило 431,1 млрд.руб.
Сборы страховых премий из года в год растут. Ряд представленный в таблице
интервальный.
Наблюдается положительная динамика в течение всего периода. Она носит
скачкообразный характер, об этом говорят цепные абсолютные приросты и цепные
темпы роста и прироста.
В течении анализируемого периода в среднем увеличения составили 392,1
млрд.руб., в среднем за год увеличилось на 71,85 млрд.руб. или 37%.
Ускоренный рост страховых премий можно увидеть и по увеличивающемуся абсолютному значению 1%
прироста.
Заключение
В данной курсовой работе
было рассмотрено страхование и страховой рынок, его элементы, виды и состояние,
в котором они находятся в данный момент в нашей стране. В ходе работы были
сделаны следующие выводы:
Защита личных и
общественных интересов, которые появляются в процессе производства, возможна
только при наличии страхования. Страхование в условиях рыночной экономики
просто необходимо.
Страховой рынок России
находится на первоначальном этапе своего развития, хотя, надо заметить, имеет
огромные возможности. Для их реализации требуется активная поддержка данной
отрасли государством. Государство должно быстрее осознать роль страхования как
стратегического сектора экономики, тогда в России будет осуществляться переход
к рыночному росту, социально-ориентированному.
На страховом рынке
взаимодействуют стороны, заинтересованные в заключении страховых соглашений и
достижении результативности страховых операций. Этот рынок является сферой
денежных отношений, в которой объектом купли-продажи выступает специфический
товар, а именно - страховая услуга, также на этом рынке формируются её спрос и
предложение.
Самое перспективное
направление развития страхования – это страхование от экономических рисков.
Превышения активов над
обязательствами в страховой компании определяет ее платежеспособность.
Инвестирование страховых
резервов (с учетом специфики страхования) должно обеспечивать их сохранность,
финансовую устойчивость страховых операций, а также направлять страховщика
достижение максимальных конечных результатов, а не на получение краткосрочной
выгоды.
Список используемой литературы
1.
Гореева
Н.М., Демидова Л.Н., Клизогуб Л.М., Орехов С.А. Статистика: учебное пособие в
схемах и таблицах./Под ред.проф. С.А.Орехова.-М.: Эксмо, 2007.
2.
Елисеева
И.И., Юзбашев М.М. Общая теория статистики: Учебник/Под ред. И.И.Елисеевой.-М.:
Финансы и статистика, 2006.
3.
Статистический
материал с сайта http://www.ininfo.ru/mag/2005/2005-11/2005-11-002.html
4.
Статистический материал с сайта http://www.rb.ru/biz/markets/show/57/
5.
Данные
с сайта htt://www.leasingword.ru/
6.
Данные
с сайта http://www.revolution.allbest.ru
7.
Данные
с сайта http://www.fssn.ru
8.
Статистика.
Методические указания по выполнению курсовой работы. М.: ВЗФЭИ, 2006.