Задача 3
По материалам обследования бюджетов домашних хозяйств одного из регионов РФ имеется следующее распределение домашних хозяйств городской и сельской местности по уровню среднедушевого дохода:
|
Группы населения по среднемесячному душевому доходу, руб. |
Город |
Село |
|
До 300 |
13,4 |
15,2 |
|
300-600 |
56,0 |
65,4 |
|
600-900 |
47,6 |
59,2 |
|
900-1200 |
33,5 |
31,3 |
|
1200-1500 |
21,5 |
15,7 |
|
1500-1800 |
17,7 |
16,0 |
|
1800-2100 |
13,5 |
12,3 |
|
2100-2400 |
9,0 |
8,2 |
|
2400-2700 |
1,2 |
0,9 |
|
2700-3000 |
0,9 |
0,5 |
|
Св. 3000 |
0,2 |
0,1 |
Оцените дифференциацию доходов населения городской и сельской местности регионов, рассчитав:
1. среднедушевой доход 10% самого богатого и самого бедного населения.
2. коэффициент фондов.
Сделайте выводы.
Решение
|
Группы населения по среднемесячному душевому доходу, руб. |
Численность населения |
Сумма накопленных частот |
||
|
Город |
Село |
Город |
Село |
|
|
До 300 |
13,4 |
15,2 |
13,4 |
15,2 |
|
300-600 |
56,0 |
65,4 |
69,4 |
80,6 |
|
600-900 |
47,6 |
59,2 |
117 |
139,8 |
|
900-1200 |
33,5 |
31,3 |
150,5 |
171,1 |
|
1200-1500 |
21,5 |
15,7 |
172 |
186,8 |
|
1500-1800 |
17,7 |
16,0 |
189,7 |
202,8 |
|
1800-2100 |
13,5 |
12,3 |
203,2 |
215,1 |
|
2100-2400 |
9,0 |
8,2 |
212,2 |
223,3 |
|
2400-2700 |
1,2 |
0,9 |
213,4 |
224,2 |
|
2700-3000 |
0,9 |
0,5 |
214,3 |
224,7 |
|
Св. 3000 |
0,2 |
0,1 |
214,5 |
224,8 |
1. Максимальные доходы 10% наименее обеспеченного населения будут равны:
по городу:
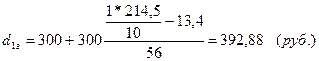
по селу
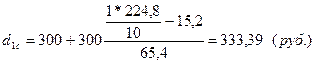
минимальные доходы 10% самого богатого населения составят:
по городу:
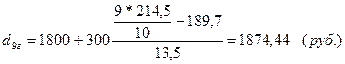
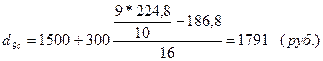
Таким образом, децильные коэффициенты дифференциации доходов населения в регионах составят:
по городу:
![]()
т.е. минимальные доходы 10% богатых превышают максимальные доходы 10% самых бедных в 4,73 раза.
По селу:
![]()
т.е. минимальные доходы 10% богатых превышают максимальные доходы 10% самых бедных в 5,37 раза.
Таким образом, в селе наблюдается более высокий уровень дифференциации доходов населения.
2.
|
Город |
Село |
||
|
Среднедушевой доход, руб. |
Численность населения, тыс. руб. |
Среднедушевой доход, руб. |
Численность населения, тыс. руб. |
По 10% самых малообеспеченных граждан |
|||
|
До 300 |
13,4 |
До 300 |
15,2 |
|
300 - 392,88 |
8,05 |
300 - 333,29 |
7,28 |
|
Итого |
21,45 |
Итого |
22,48 |
По 10% самых богатых граждан |
|||
|
1877,44 - 2100 |
10,15 |
1791 - 1800 |
0,48 |
|
2100-2400 |
9,0 |
1800 - 2100 |
12,3 |
|
2400-2700 |
1,2 |
2100-2400 |
8,2 |
|
2700-3000 |
0,9 |
2400-2700 |
0,9 |
|
Св. 3000 |
0,2 |
2700-3000 |
0,5 |
Итого |
21,45 |
Св. 3000 |
0,1 |
|
|
|
Итого |
22,48 |
Среднедушевой доход 10% самого бедного населения:
По городу:
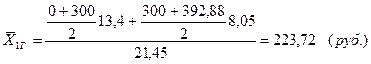
по селу:
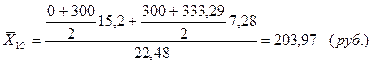
среднедушевой доход 10% самого богатого населения:
|
Группы насел. |
Числ. нас |
Серед. интер. |
Х*f |
Группы насел. |
Числ. нас |
Серед. интер. |
Х*f |
|
1877,44 - 2100 |
10,15 |
1988.72 |
20185.51 |
1791 - 1800 |
0,48 |
1795,5 |
861,84 |
|
2100-2400 |
9,0 |
2250 |
20250 |
1800 - 2100 |
12,3 |
1950 |
23985 |
|
2400-2700 |
1,2 |
2550 |
3060 |
2100-2400 |
8,2 |
2250 |
18450 |
|
2700-3000 |
0,9 |
2850 |
2565 |
2400-2700 |
0,9 |
2550 |
2295 |
|
Св. 3000 |
0,2 |
3150 |
630 |
2700-3000 |
0,5 |
2850 |
1425 |
Итого |
21,45 |
|
46690,51 |
Св. 3000 |
0,1 |
3150 |
315 |
|
|
|
Итого |
22,48 |
|
47331,84 |
По городу:
![]()
по селу:
![]()
коэффициент фондов по городу:
![]()
т.е. среднемесячные душевые доходы 10% самых богатых города выше среднемесячных душевых доходов 10% самых бедных в 9,73 раза.
коэффициент фондов по селу:
![]()
т.е. среднемесячные душевые доходы 10% самых богатых села выше среднемесячных душевых доходов 10% самых бедных в 10,32 раза.
Таким образом, и этот показатель свидетельствует о том, что по селу наблюдается более высокий уровень дифференциации доходов населения.
Задача 4
По данным задания 3 проведите перегруппировку населения по децильным группам, по каждой группе вычислите долю населения и долю совокупного дохода. Постройте кривую Лоренца. Определите коэффициенты концентрации доходов Джинни, Лоренца.
Решение
|
Группы населения по среднемесячному душевому доходу, руб. |
Численность населения |
Сумма накопленных частот |
||
|
Город |
Село |
Город |
Село |
|
|
До 300 |
13,4 |
15,2 |
13,4 |
15,2 |
|
300-600 |
56,0 |
65,4 |
69,4 1 |
80,6 |
|
600-900 |
47,6 |
59,2 |
117 |
139,8 |
|
900-1200 |
33,5 |
31,3 |
150,5 |
171,1 |
|
1200-1500 |
21,5 |
15,7 |
172 |
186,8 |
|
1500-1800 |
17,7 |
16,0 |
189,7 |
202,8 |
|
1800-2100 |
13,5 |
12,3 |
203,2 |
215,1 |
|
2100-2400 |
9,0 |
8,2 |
212,2 |
223,3 |
|
2400-2700 |
1,2 |
0,9 |
213,4 |
224,2 |
|
2700-3000 |
0,9 |
0,5 |
214,3 |
224,7 |
|
Св. 3000 |
0,2 |
0,1 |
214,5 |
224,8 |
Рассчитаем децильные группы:
Для города:
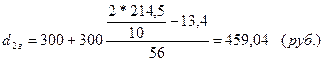
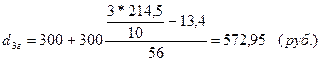

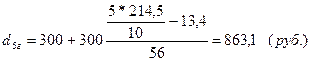
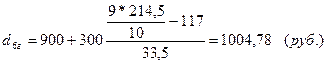
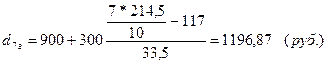
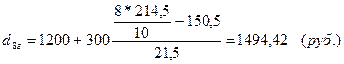
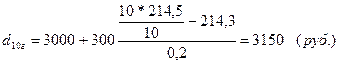
Для города:
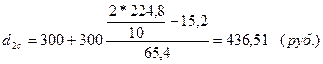
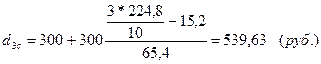
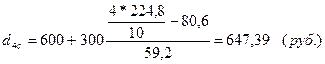
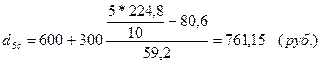
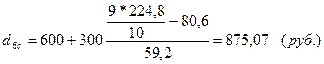
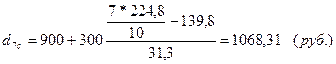
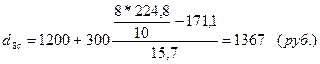
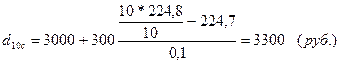
|
|
Город |
Село |
|
|
Денежные доходы - всего |
100,00 |
100,00 |
|
|
В том числе по 10% группам населения |
|
|
|
|
Первая |
3,36 |
2,99 |
|
|
Вторая |
3,91 |
3,92 |
|
|
Третья |
4,91 |
4,85 |
|
|
Четвертая |
5,88 |
5,82 |
|
|
Пятая |
7,38 |
6,85 |
|
|
Шестая |
8,59 |
7,87 |
|
|
Седьмая |
10,23 |
9,61 |
|
|
Восьмая |
12,78 |
12,29 |
|
Девятая |
16,03 |
16,12 |
|
|
Десятая |
26,93 |
29,68 |
|
Рассчитаем коэффициент Лоренца:
![]()
в городе:
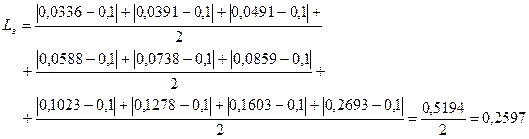
в селе:
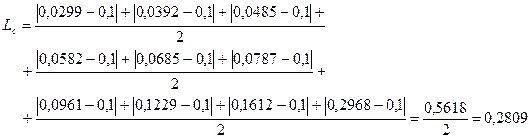
Так как в селе коэффициент Лоренца в несколько выше, чем в городе, можно утверждать, что в селе наблюдается большая концентрация доходов у самых обеспеченных групп населения.
Для построения кривой Лоренца и коэффициента концентрации доходов Джини необходимо произвести ряд дополнительных расчетов:
|
10% группы населения по уровню среднедушевого дохода |
Доля в совокупном доходе |
Расчетные показатели |
|||||||
|
Город |
Село |
||||||||
|
Xi |
SumXi |
Город |
Село |
Sum Yiг |
XiYi |
Sum XiYiг |
Sum Yiс |
XiYiс |
Sum XiYiс |
|
0,1 |
0,1 |
0,033593 |
0,029983 |
0,033593 |
0,003359 |
0,003359 |
0,029983 |
0,002998 |
0,002998 |
|
0,1 |
0,2 |
0,039164 |
0,039256 |
0,072757 |
0,003916 |
0,007275 |
0,069239 |
0,003926 |
0,006924 |
|
0,1 |
0,3 |
0,04899 |
0,04853 |
0,121747 |
0,004899 |
0,012174 |
0,11777 |
0,004853 |
0,011777 |
|
0,1 |
0,4 |
0,058815 |
0,058221 |
0,180562 |
0,005881 |
0,018056 |
0,175991 |
0,005822 |
0,017599 |
|
0,1 |
0,5 |
0,073799 |
0,068452 |
0,25436 |
0,00738 |
0,025436 |
0,244443 |
0,006845 |
0,024444 |
|
0,1 |
0,6 |
0,085913 |
0,078697 |
0,340273 |
0,008591 |
0,034027 |
0,32314 |
0,00787 |
0,032314 |
|
0,1 |
0,7 |
0,102337 |
0,096076 |
0,442611 |
0,010234 |
0,044261 |
0,419216 |
0,009608 |
0,041921 |
|
0,1 |
0,8 |
0,127779 |
0,122938 |
0,57039 |
0,012778 |
0,057039 |
0,542154 |
0,012294 |
0,054215 |
|
0,1 |
0,9 |
0,160272 |
0,161069 |
0,730662 |
0,016027 |
0,073066 |
0,703223 |
0,016107 |
0,070322 |
|
0,1 |
1 |
0,269338 |
0,296777 |
1 |
0,026934 |
0,1 |
1 |
0,029678 |
0,1 |
|
1 |
|
1 |
1 |
|
0,1 |
0,374693 |
|
0,1 |
0,362513 |
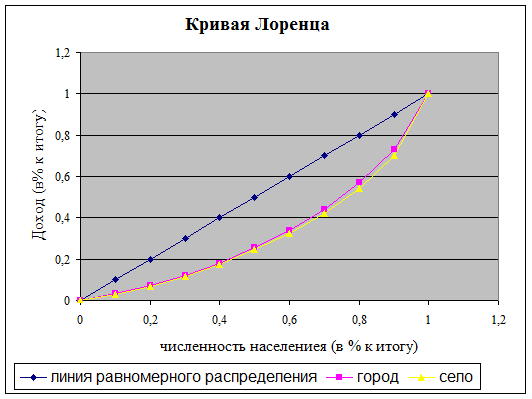
Характеристику степени неравенства в распределении населения по доходу можно получить, рассчитав коэффициент Джини по формуле:
![]()
по городу:
Gг = 1 - 2 * 0,374693 + 0,1 = 0,3506
По селу:
Gг = 1 - 2 * 0,362513 + 0,1 = 0,3750
В селе уровень неравенства населения по доходу выше.
Задача 5.
На основе х2 определите, является ли "закрытая зона" факторами заболеваемости туберкулезом:
|
|
Состояние здоровья |
Итого |
|
Болен |
Здоров |
||
|
"Закрытая зона" |
34 |
966 |
1000 |
|
Остальное население |
16 |
4984 |
5000 |
|
Итого |
50 |
5950 |
6000 |
Решение
Рассчитаем коэффициент сопряженности Пирсона:
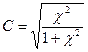
![]()
На 79,34% закрытая зона является фактором заболеваемости туберкулезом.
Так же для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп применяют коэффициенты ассоциации.
Для вычисления строится таблица, показывающая связь между двумя явлениями, каждое из которых должно быть альтернативным:
|
Факторный признак |
Результативный признак |
|||
|
1 |
2 |
Итого |
||
|
1 2 |
А С |
В D |
А + В С + D |
|
Итого |
А+С |
В + D |
А+В+С+D |
|
Коэффициент ассоциации рассчитывается по формуле:
![]()
![]()
Связь можно считать подтвержденной, так как Ка > 0,5.