- Доказать
равенство, используя свойства операций над множествами (A\B)È(AÇC)=A\(B\C)
Решение
Для этого докажем два включения: (A\B)È(AÇC)ÌA\(B\C) и (A\B)È(AÇC)ÉA\(B\C)
Пусть xÎ(A\B)È(AÇC), значит
xÎ(A\B) или xÎ(AÇC )
xÎA и xÏB или xÎA и
xÎC
xÎA и xÏ(B\C) или xÎA и
xÏ(B\C)
xÎA\(B\C)
второе включение аналогично,
пусть xÎA\(B\C),
значит
xÎA и xÏ(B\C)
xÎA и (xÎB и xÎС или xÏB)
xÎA и xÎB и xÎС или xÎA и xÏB
xÎ(AÇC) или xÎ(A\B)
xÎ(A\B)È(AÇC)
2.
Пусть имеется множество А={1,2,3,4}, на этом множестве
определены отношения RÌA2 и RÌA2
а. Определить является ли отношение Р рефлексивным
б. Построить графические представления отношений P, R, P°R
в. Найти область определений и область значений для отношений P, R, P°R
Решение.
а. Отношение P не является
рефлексивным.
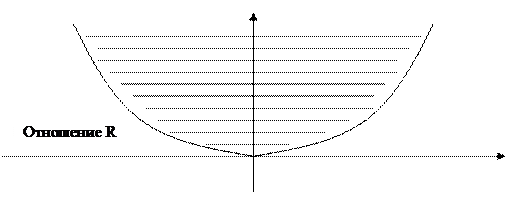 б,в.
б,в.
Соответственно область
определения и значения для отношения R:
(1,1) (1,2) (1,3)
(1,4)
(2,2) (2,3) (2,4)
(3,4)
Соответственно область
определения и значения для отношения P:
(1,2) (2,1) (1,4)
(4,1)
Соответственно область определения
и значения для отношения P°R:
(1,x) (2,x) (4,y) , где xÎA, yÎA\{1}
3.
Сколько 4-хзначных чисел можно получить из числа
1122334456780
Решение.
Всего 13 цифр, из которых 12
ненулевых, следовательно, из 12 цифр получится:
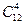 за вычетом
повторяющихся и симметричных, которых составит :
за вычетом
повторяющихся и симметричных, которых составит :
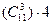 - повторяющихся
- повторяющихся
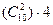 - симметричные
и плюс числа с 0 (3 типа), которых соответственно:
- симметричные
и плюс числа с 0 (3 типа), которых соответственно:
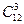 за вычетом
повторяющихся и симметричных, которых составит :
за вычетом
повторяющихся и симметричных, которых составит :
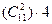 - повторяющихся
- повторяющихся
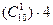 - симметричные
Результат:
- симметричные
Результат: 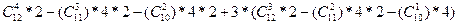 где
где
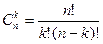
4.
Управление А имеет а предприятий, из них а1
выпускают продукцию А, а2 – B, a3
– C, a4 – A и B, a5 – B и C, a6 – A и C, a7 – A и B и C. Сколько предприятий
а. выпускают ровно один вил продукции
б. не выпускает ни одного продукта
Решение.
120 50 30 - производители продукта *
A B C - продукт *
8 8 8 - a7
32 32 --- - a4-a7
--- 2 2 - a5-a7
12 --- 12 - a6-a7
52 42 22 - сумма предыдущих 4 пунктов = производящие не
только продукт *
а. Значит: A – 68
B – 8
C – 8
б. Не выпускают данные продукты : 20
5.
Найти последовательность аn ,
удовлетворяющей рекуррентному соотношению b×an+2+c×an+1+ d×an и начальным условиям.
Решение.
2*an-2-5*an-1+2*an=0
n=3: 12-15+2*a3=0 a3=1.5
n=4: 6-7.5+2*a4=0 a4=0.75
В силу линейности: 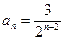
6.
1. СКНФ, СДНФ
2. Минимальную ДНФ
а. методом Квайна
б. с помощью карт Карно
Решение.
1. 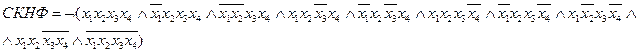
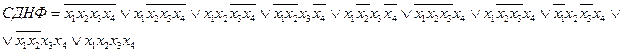 где
где 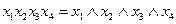
2.а. 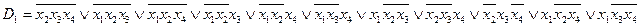
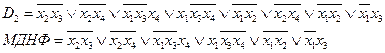
2.б.
|
x3,4
x1,2
|
0
|
0
|
1
|
1
|
|
0
|
1
|
1
|
0
|
|
0
|
0
|
1
|
1
|
1
|
1
|
|
0
|
1
|
0
|
1
|
0
|
0
|
|
1
|
1
|
1
|
0
|
1
|
0
|
|
1
|
0
|
1
|
1
|
0
|
1
|
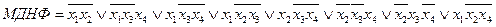
7.
Требуется
а. Нарисовать граф
б. Найти степенную последовательность графа
в. Найти матрицу смежности графа
г. Обозначить рёбра и найти матрицу инцидентности
д. Определить количество компонент связанности
е. Найти 4 простых цикла
ж. Найти минимальный остов и его вес
Решение.
а.
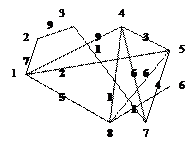 б.
(4,2,2,4,4,1,3,4)
б.
(4,2,2,4,4,1,3,4)
в.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
|
2
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
|
3
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
|
4
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
|
5
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
|
6
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
|
7
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
|
8
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
г.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
(1,2,7)
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
(1,4,9)
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
|
(1,5,2)
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
|
(1,8,5)
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
|
(2,3,9)
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
|
(3,7,1)
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
|
(4,5,3)
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
|
(4,7,6)
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
|
(4,8,1)
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
|
(5,7,4)
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
|
(5,8,6)
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
|
(6,8,1)
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
 д.
2 компонента связности
д.
2 компонента связности
е. {1,5,8}, {1,4,5}, {4,5,8}, {1,4,8}
ж. вес: 19
8. Найти минимальный автомат,
эквивалентный данному
Задача 141
|
0
|
1
|
|
1
2
3
4
5
6
7
8
9
|
2,0
8,1
8,1
3,0
2,0
4,0
9,0
5,1
2,0
|
4,1
7,0
6,0
5,1
4,1
8,1
8,1
3,1
9,1
|
Решение:
Минимальным является автомат без
повторений
|
0
|
1
|
|
1
2
3
4
5
6
7
|
2,0
8,1
3,0
2,0
4,0
9,0
5,1
|
4,1
7,0
5,1
4,1
8,1
8,1
3,1
|
|
0
|
1
|
|
1
2
3
4
5
|
8,1
3,0
2,0
4,0
5,1
|
7,0
5,1
4,1
8,1
3,1
|