Вариант № 1
Задача 1. Охарактеризуйте динамику структуры совокупности лиц, совершивших преступления в течение первого полугодия 2001 года, в зависимости от вида занятия, имеемых в период совершения преступления:
|
Виды занятия |
Численность зарегистрированных преступников, тыс. чел. |
|
|
1 квартал |
2 квартал |
|
|
Наемные работники гос. и муницип. предприятий |
8,4 |
10,2 |
|
Наемные работники частных предприятий |
14,2 |
14,1 |
|
Частные предприниматели |
8,6 |
9,2 |
|
Безработные |
14,3 |
12,5 |
|
Прочие |
14,8 |
11,8 |
|
Σ |
60,3 |
57,8 |
a) Относительная величина динамики
1 квартал:
1) 8,4 / 60,3 * 100% = 13,93%
2) 14,2 / 60,3 * 100% = 23,71%
3) 8,6 / 60,3 * 100% = 14,26%
4) 14,3 / 60,3 * 100% = 23,71%
5) 14,8 / 60,3 * 100% = 24,54%
2 квартал:
1) 10,2 / 57,8 * 100% = 17,65%
2) 14,1 / 57,8 * 100% = 24,39%
3) 9,2 / 57,8 * 100% = 15,92%
4) 12,5 / 57,8 * 100% = 21,63%
5) 11,8 / 57,8 * 100% = 20,42%
Теперь сравним первый и второй квартал:
1) 17,65 - 13,93 = 3,72% - численность преступников среди наемных работников гос. и муницип. предприятий во 2 квартале больше по сравнению с 1 кварталом на 3,72%
2) 24,39 - 23,71 = 0,68% - численность преступников среди наемных работников частных предприятий во 2 квартале больше по сравнению с 1 кварталом на 0,68%
3) 15,92 - 14,26 = 1,66% - численность преступников среди частных предпринимателей во 2 квартале больше по сравнению с 1 кварталом на 1,66%
4) 21,63 - 23,71 = - 2,08% - численность преступников среди безработных во 2 квартале меньше по сравнению с 1 кварталом на 2,085%
5) 20,42 - 24,54 = - 4,12 - численность преступников среди прочих во 2 квартале меньше по сравнению с 1 кварталом на 4,12%.
Задача 2. Рассчитайте степенную и структурные средние по распределению уголовных дел, в зависимости от срока расследования:
|
Срок расследования, месяц |
Число уголовных дел |
|
До 1 |
8 |
|
1 – 2 |
34 |
|
2 – 3 |
26 |
|
3 – 4 |
11 |
|
4 – 6 |
3 |
|
6 - 12 |
5 |
|
12 и более |
3 |
a) Средняя арифметическая взвешенная
х = Σxi*fi / Σfi
Σfi = (8+34+226+11+3+5+3) = 90
Σxi * fi = (0,5*8) + (1,5*34) + (2,5*26) + (3,5*11) + (5*3) + (9*5) + (15*3) = 258,3
|
Середина интервала |
xi*fi |
|
0,5 |
4 |
|
1,5 |
51 |
|
2,5 |
59,8 |
|
3,5 |
38,5 |
|
5 |
15 |
|
9 |
45 |
|
15 |
45 |
|
|
Σxi*fi = 258,3 |
х = 258,3 /90 = 2,87 - средняя арифметическая взвешенная.
b) Структурные средние - мода
Мода Mo = xo + i * (fmo – fmo-1 / 2 fmo – fmo – 1 – fmo + 1)
Mo = 2 + 2 * ((26 – 34) / (26 – 34 - 11) = 2 + 2 * (- 8 / - 11) = 2, 84
Xo = 2 – начало модального интервала (интервал 2-3)
c) Медиана
Me = xo + i * ((E f / 2 – S) / (fme))
Σf / 2 = 90 / 2 = 45
Me = 2 + 1 * ((45 - 42) / 26) = 2,12
Из выше приведенных расчетов можно сделать вывод, что средний срок расследования преступлений приходится на временной интервал соответствующий 2-3 месяцам
Задача 3. выясните, какой из представленных показателей отличается большей вариативностью значений в рассматриваемый период:
|
Год |
Число зарегистрированных должностных преступлений в районе А |
Численность привлеченных к уголовной ответственности, вследствие должностных преступлений |
|
1991 |
18 |
32 |
|
1992 |
20 |
24 |
|
1993 |
16 |
19 |
|
1994 |
17 |
14 |
|
1995 |
14 |
17 |
|
1996 |
15 |
18 |
|
1997 |
14 |
17 |
|
1998 |
15 |
16 |
|
1999 |
18 |
13 |
|
2000 |
19 |
10 |
|
2001 |
18 |
11 |
Для этого необходимо вычислить коэффициент вариации
a) Коэффициент вариации V = (δ / Ef) * 100%
b) Среднеквадратическое отклонение δ = √δ2
c) Дисперсия δ2= (Σ (|xi - x|)2 / n)
Для района А
xi = 184 / 11 = 16,7 - средняя арифметическая
δ2= 7,22 / 11 = 50,41/11 = 4,58
δ = √ 4,58 = 2,14
V = 2,14 / 184 * 100% = 1,16% - вариативность района А
Для числа привлеченных к ответственности
xi = 191 / 11 = 17,4
δ2= 15,22 / 11 = 231,04/11 = 21
δ = √ 21 = 4,58
V = 4,58 / 191 * 100% = 2,4% - вариативность числа привлеченных к ответственности.
|
X i |
Для числа зарегистрированных преступлений в районе А |
X i |
Для числа привлеченных к уголовной ответственности |
|
|Xi - X| |
|Xi - X| |
||
|
18 |
1,3 |
32 |
14,6 |
|
20 |
3,3 |
24 |
6,6 |
|
16 |
- 0,7 |
19 |
1,6 |
|
17 |
0,3 |
14 |
3,4 |
|
14 |
-2,7 |
17 |
- 0,4 |
|
15 |
1,7 |
18 |
0,6 |
|
14 |
- 2,7 |
17 |
- 0,4 |
|
15 |
1,7 |
16 |
- 1,4 |
|
18 |
1,3 |
13 |
4,4 |
|
19 |
2,3 |
10 |
- 7,4 |
|
18 |
1,3 |
11 |
- 6,4 |
|
|
Σ |Xi - X| = 7,1 |
|
Σ |Xi - X| = 15,2 |
Показатель района А отличается большей вариативностью, а второй меньшей вариативностью.
Задача 4. Охарактеризуйте динамику уровня смертности населения от самоубийств в стране за период 1995-2001 годы, рассчитав базисные цепные и средние показатели: абсолютного прироста, темп роста, темп прироста; цепные показатели абсолютного значения 1% прироста. Спрогнозируйте число самоубийств в 2002 году на основе уравнения тренда, построенного по линейной функции методом аналитического выравнивания. Постройте график фактической динамики уровня смертности найденной линии тренда.
|
Год |
Число преступлений, совершенных несовершеннолетними и при их соучастии, тыс. |
|
1995 |
1430 |
|
1996 |
1520 |
|
1997 |
1987 |
|
1998 |
2860 |
|
1999 |
3220 |
|
2000 |
2905 |
|
2001 |
2530 |
a) Основные показатели изменения уровня
|
Год |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
|
Число преступлений, совершенных несовершеннолетними и при их соучастии, тыс. |
1430 |
1520 |
1987 |
2860 |
3220 |
2905 |
2530 |
|
Абсолютный прирост, число самоубийств цепные базисные |
- - |
- 90 - 90 |
- 467 - 557 |
- 883 - 1480 |
- 360 - 1790 |
315 - 1475 |
375 - 1100 |
|
Темп роста, доли цепные базисные |
- - |
0,941 1,063 |
0,765 1,389 |
0,695 2 |
0,888 2,25 |
1,108 2,03 |
1,148 1,769 |
|
Темпы прироста, доли цепные базисные |
- - |
- 5,9 6,3 |
-23,5 38,9 |
30,5 100 |
-11,2 125 |
10,8 103 |
14,8 76,9 |
|
Абсолютное значение 1% прироста |
- |
15,25 |
19,87 |
-28,62 |
32,14 |
29,2 |
25,34 |
Средний абсолютный прирост ∆y = (-90 - 467 – 873 - 360 + 315+ 375) / 6 = - 1100
Темп роста Тр = 5,545 / 6 = 0,92,42 = 92,42%
Темп прироста Тпр = 92,42% – 100% = - 7,58% - темп прироста снизился на 7,58%.
b) Линейная функция y (t) = a1t + ao
|
Год |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
|
Соотношение чисел годам |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Года берем произвольные.
yt = a0 * a1t – линейная функция зависимости значения показателя от времени
где: a0 и a1 – параметры уравнения, определяемы как
a1 = Σ yt / Σt
a0 = Σy / n
a0 = a1 * 1 = 1430
a0 = a1 * 4 = 1987
a1 = 1151,5
a0 = 278,5
yt = 1151,5 + 278,5t
y1 = 1430; y2 = 1708,5; y3 = 1987; y4 = 2265,5; y5 = 2544; y6 = 2822,5; y7 = 3101
a0 = a1 * 2 = 1520
a0 = a1 * 6 = 3220
a1 = 566,67
a0 = 386,66
yt = 386,66 + 566,67t
y1 = 953,33; y2 = 1520; y3 = 2086,07; y4 = 2653,34; y5 = 3220; y6 = 3786,68; y7 = 4353,35
a0 = (1151,5 + 386,66) / 2 = 769
a1 = (278,5+ 556,67) / 2 = 417,5
yt = 769,0 + 417,5t
y1 = 1186,59; y2 = 1604,18; y3 = 2021,77; y4 = 2439,36; y5 = 2856,95; y6 = 3276,7; y7 = 3694,65
2002 год – y8
y8 = 769 + (417,59 * 8) = 4109,72
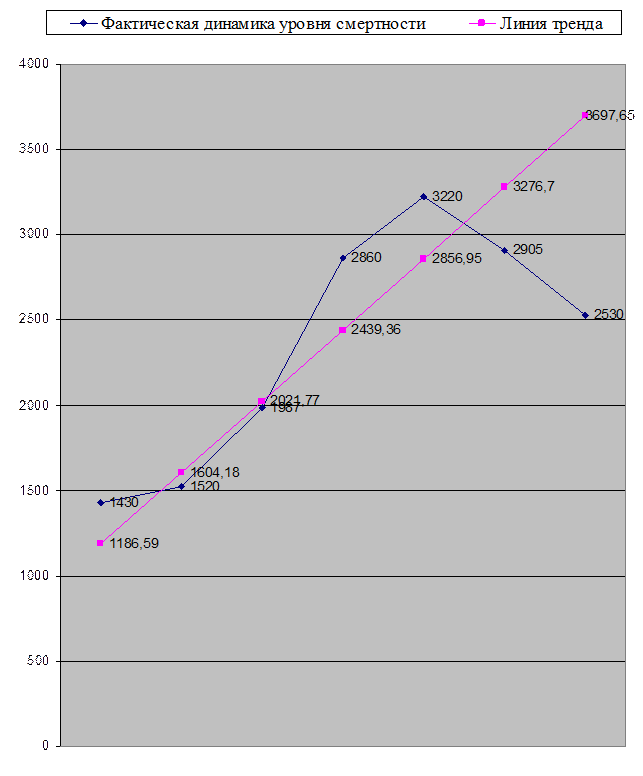
График. Теоретическая линия тренда и фактическая динамика уровня смертности
|
|
|
|
|
|
|
Задача 5. При изучении 350 уголовных дел, отобранных из общего числа возбужденных дел методом механического отбора, оказалось, что 7% из них были прекращены необоснованно. С вероятностью 0,954 определите пределы, в которых находится доля необоснованно прекращенных дел в общем, числе возбужденных уголовных дел.
a) ∆ = t * m
b) m = √ w (1 - w) / n * (1-n/N)
n = 350 * 7% / 100 =24,5 – уголовные дела, прекращенные необоснованно
24,5 * 0,954 = 23,37 – доля необоснованно прекращенных дел с вероятностью 0,954
m = √ 23,37 * (1 – 23,37) / 24,5 * (1 – 24,5 / 350) = 4,45
0,954 – t = 2
t – коэффициент (критерии) доверия
t = 1,046
∆ = 4,45 * 1,046 = 4,65
c) Границы интервала w - ∆w ﻛ d ﻛ w + ∆w
23,37 – 4,65 ﻛ d ﻛ 23,37 + 4,65
18,72 ﻛ d ﻛ 28,02
0,18 ﻛ d ﻛ 0,28
В этих пределах находится доля необоснованно прекращенных дел в общем, числе возбужденных уголовных дел.