Содержание
1. Каким
образом предприятие оптимизирует свое положение на рынке совершенной
конкуренции в краткосрочном периоде? Опишите условия кратковременного
прекращения производства предприятием. Что представляет собой краткосрочная
кривая предложения на рынке совершенной конкуренции?. 2
2. Каковы преимущества частичного
резервирования вкладов по сравнению со 100 - процентным резервированием?
Объясните, почему банки могут работать в режиме частичного резервирования
вкладов. Если допустить, что центральный банк не регулирует размер обязательных
резервов, стремились бы коммерческие банки установить нулевой уровень своих
резервов?. 9
Задача 4. 12
Список литературы.. 13
1. Каким образом предприятие оптимизирует свое положение на рынке
совершенной конкуренции в краткосрочном периоде? Опишите условия
кратковременного прекращения производства предприятием. Что представляет собой
краткосрочная кривая предложения на рынке совершенной конкуренции?
Краткосрочным периодом называется
такой период, в течение которого производственные мощности каждого предприятия
(размеры и число заводов, фабрик, других производственных единиц) фиксированы,
но выпуск может быть увеличен или снижен за счет изменения объема использования
переменных факторов. Общее число предприятий в отрасли остается неизменным.
Заметим, что в условиях совершенной конкуренции предприятие является ценополучателем.
В
краткосрочном периоде предприятие может оптимизировать свое положение на рынке
совершенной конкуренции, производя такой объем продукции, при котором
максимальны прибыли или минимальны убытки. Существует два подхода к
анализу: 1) сравнение валового дохода и
общих издержек, 2) сравнение предельного дохода и предельных издержек.
Рассмотрим первый подход.[1]
В краткосрочном периоде общие издержки фирмы делятся на
постоянные и переменные. Постоянные издержки должны быть полностью оплачены
даже в том случае, когда фирма уже прекратила свое существование. И если фирма
ничего не производит, то в краткосрочном периоде она несет убытки, равные постоянным
издержкам. Это означает, что, хотя фирма, возможно, не в состоянии получить
прибыль ни при каком объеме выпуска, она все же могла бы заниматься
производством, если бы ей удалось нести меньшие убытки, чем те постоянные
издержки, которые ей так или иначе пришлось бы возмещать в случае закрытия.
Рассмотрим теперь с помощью графиков, в каком случае фирма
будет максимизировать прибыль, а в каком – минимизировать убытки.
Заметим,
что экономисты называют максимумом прибыли как максимум положительной разницы
между выручкой и затратами производства продукции, так и минимум отрицательной
разности между теми же величинами. Поэтому минимум убытков может
рассматриваться как максимум прибыли, если получить положительную прибыль
невозможно.
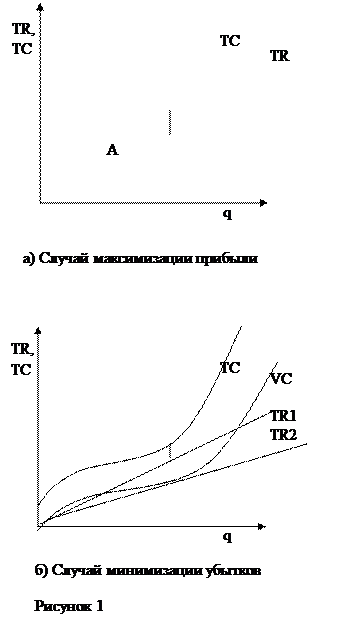
Пусть TC на рис. 1,
представляет кривую общих затрат типичного предприятия в коротком
периоде, VC – кривую
переменных затрат, луч TR - линию его общей выручки. Наклон линии TR неизменен
на всем ее протяжении, поскольку цена не зависит от объема выпуска данного
предприятия, и потому TR = P*q.
Прибыль
предприятия представляет разность между общей выручкой и общими затратами
краткосрочного периода:
П(q) =
TR(q) - TC(q)
Как было замечено выше, TR представляет собой прямую линию, в то время как TC – это кривая. Общие издержки
возрастают с ростом производства: его расширение требует большого количества
ресурсов.
Но темпы
увеличения общих издержек различаются в зависимости от уровня эффективности
фирмы. С течением времени темпы роста общих издержек постепенно замедляются, если
фирма использует свои постоянные ресурсы более эффективно. Потом валовые
издержки начинают увеличиваться ускоренными темпами вследствие неэффективности,
которая сопутствует чрезмерной эксплуатации оборудования фирмы.
На рис.1а
показан случай максимизации прибыли. Точки А и В, где равны общие издержки и
общая выручка, соответствуют точкам безубыточности (нормальной прибыли). Любое
производство за пределами этих точек принесет экономическую прибыль.
Максимальная прибыль достигается там, где разница (по вертикали) между валовым
доходом и валовыми издержками наиболее велика (на графике она отмечена
вертикальной линией).
На
рис.1б рассмотрен случай минимизации
убытков. Пусть цена установилась на таком уровне (меньшем, чем в пункте а)),
что TR1 – прямая общей выручки фирмы. Здесь валовой доход превосходит
совокупные переменные издержки, но меньше общих издержек. В этом случае фирма
будет продолжать производство, поскольку может оплатить некоторую часть своих
постоянных издержек из этого дохода. В
случае закрытия фирмы все постоянные издержки ей придется оплачивать. При
производстве же продукции ее убытки будут меньше постоянных издержек. Убытки минимальны там, где разница между валовыми издержками и валовым
доходом наименьшая (на графике она показана чертой).
Если цена
на продукцию фирмы станет еще меньше и совокупный доход будет характеризовать
прямая TR2, то фирма
прекратит производство. В этом случае производство любого объема сопряжено с
убытками, превышающими постоянные издержки, которые фирма потеряет, прекратив
свое существование. В случае закрытия фирма минимизирует свои убытки путем
остановки производства, то есть при нулевом выпуске.
Перейдем ко второму подходу. Здесь сопоставляется предельный
доход с предельными издержками.[2]
Этот подход состоит в сравнении величин, которые каждая
дополнительная единица продукта добавляет к валовому доходу и общим издержкам.
Любую единицу продукта, предельный доход от которой превышает связанные с ней
предельные издержки, следует производить, поскольку от продажи каждой такой
единицы фирма получает больше дохода, чем добавляет к издержкам при ее
производстве. Точно так же, если предельные издержки производства единицы
продукта превышают порождаемый ею предельный доход, фирме следует отказаться от
выпуска этой единицы, так как она себя не окупит.
Как было
замечено выше, прибыль предприятия вычисляется следующим образом:
П(q) = TR(q) -
TC(q).
Условием
максимизации прибыли первого порядка
будет, очевидно,
[dП(q)]/dq = [dTR(q)/dq] - [dTС(q)/dq] = 0,
а поскольку dTR(q)/dq
= MR(q) и dTC(q)/dq = MC(q),
условием первого порядка является равенство предельной выручки предельным
затратам:
MR(q*) = MC(q*).
Но для совершенно
конкурентного предприятия Р = AR = MR, и, следовательно, условие первого
порядка может быть представлено и как равенство предельных затрат цене: MC(q*) = P. Таким
образом, фирма максимизирует прибыли или минимизирует убытки, когда ее
производство соответствует точке, в которой предельные издержки равны
предельному доходу (и цене продукции).
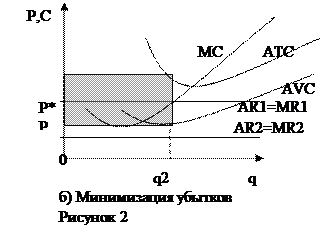
На рис.2а) каждая единица продукта до q1 включительно добавляет к валовому доходу больше, чем
к предельным издержкам. Так что цена (и предельный доход) превосходит
предельные издержки для всех первых q1 единиц
продукта, следовательно, их надо производить. Следующая единица добавит к
издержкам больше, чем к доходу, поэтому произведена не будет. Экономическую
прибыль легко подсчитать: П= q1*p* – ATC*q1 = (p*-ATC)*q1. На рисунке она обозначена темным прямоугольником.
Нужно заметить, что фирма стремится максимизировать именно свою совокупную
прибыль, а не прибыль в расчете на единицу продукта.
На рис.2б)
представлена ситуация, когда цена продукта Р* (MR1) превосходит минимальную величину средних переменных
издержек, но остается меньше средних общих издержек. В этом случае фирме
выгодно произвести q2 единиц
продукции. При любом другом объеме производства сумма убытков будет выше. Здесь
же убытки равны верхнему темному прямоугольнику. Если фирма выберет закрытие
производства, то ее убытки будут равны постоянным издержкам, которые обозначены
большей областью - двумя закрашенными прямоугольниками. Если цена продукта
составит Р (MR2), что
ниже минимальной величины средних переменных издержек, то фирма минимизирует
свои издержки в краткосрочном периоде, прекратив свое существование. В этом
случае не существует объема производства, при котором фирма могла бы нести
убытки ниже своих совокупных постоянных издержек.
Случай прекращения производства несколько
видоизменяет правило равенства предельного дохода и предельных издержек:
конкурентная фирма максимизирует свои прибыли или минимизирует убытки в
краткосрочном периоде, производя такой объем продукта, при котором предельный
доход равен предельным издержкам, но при условии, что цена превосходит
минимальную величину средних переменных издержек.
Далее
рассмотрим краткосрочную кривую предложения фирмы на рынке
совершенной конкуренции.[3]
Функцией предложения от цены
называют зависимость величины предложения от цены данного товара. Можно
показать, что кривая предложения совершенно конкурентного предприятия в
краткосрочном периоде тождественна части его кривой предельных затрат.
Рисунок 3.
Построение кривой предложения в краткосрочном периоде.
На
рис. 3а представлены кривые предельных (MC), средних общих (ATC) и средних
переменных (AVC) затрат. При цене P1 максимум прибыли достигается
при выпуске q1 значит, точка А на кривой MC принадлежит кривой
предложения фирмы. При более низкой цене, P2, прибыль будет
максимальна при выпуске q2; значит, и точка В на кривой MC
принадлежит кривой предложения. Нужно заметить, что в этом случае максимум
прибыли равен нулю, поскольку цена P2 равна минимуму средних общих
затрат (P2 = AR = MR = min ATC).Если цена
снизится до P3 < ATC, прибылемаксимизирующий
объем производства упадет до q3. Прибыль в этом случае будет
отрицательна, поскольку точка С на кривой MC лежит ниже кривой ATC и, значит,
выручка от продажи выпуска q3 не возместит общих затрат его
производства: P3*q3 < ATC(q3)*q3. Но P3
> AVC(q3), значит, выручка от продажи выпуска q3
возместит все переменные и, кроме того, часть постоянных затрат предприятия.
Таким образом, убытки от выпуска q3 будут меньше, чем сумма общих
постоянных затрат. Поэтому по сравнению с нулевым выпуском выпуск q3
будет прибылемаксимизирующим. Следовательно, точка С
принадлежит кривой предложения предприятия. При еще более низкой цене P4
= minAVC выпуск q4 удовлетворяет условиям
максимизации прибыли. Это значит, что TR(q4) = q4*(AVC(q4))
= TVC(q4) и, следовательно, убытки предприятия равны сумме
постоянных затрат. В этих условиях предприятию безразлично, производить ли q4
единиц продукции или закрыться. Поэтому точку D на кривой MC называют точкой
закрытия. Эта точка может принадлежать кривой предложения предприятия, а может
и не принадлежать. Наконец, при цене P5 = minMC
выпуск q5 также удовлетворяет условиям максимизации, но цена не
возмещает средних переменных затрат (P5 < AVC(q5)), и
при любом отличном от нуля выпуске убытки окажутся выше постоянных затрат.
Следовательно, в этом случае нулевой выпуск окажется оптимальным. То есть при Р
< minAVC предприятие предпочтет закрыться. Поэтому
точка Е на кривой MC не принадлежит кривой предложения совершенно конкурентного
предприятия.
Кривая
предложения совершенно конкурентного предприятия представлена на рис.3б. Здесь
точки А' , В' , С' , D' соответствуют точкам А, В, С, D кривой MC на рис. 3а.
Множество таких точек формирует участок кривой предложения, лежащий выше точки
D', соответствующей минимуму AVC на рис. 3a. Таким образом, кривая предложения
совершенно конкурентного предприятия в краткосрочном периоде представляет собой
возрастающую ветвь кривой предельных затрат, которая лежит выше минимума
средних переменных затрат. При более низком, чем minAVC,
уровне рыночной цены кривая предложения совпадает с осью цен (участок OP4
на рис. 3б). Если функции средних переменных и предельных затрат известны,
определить функцию предложения совершенно конкурентного предприятия можно так:
q=S(P),еслиР>minAVC, q = 0, если Р < minAVC.
2. Каковы
преимущества частичного резервирования вкладов по сравнению со 100 - процентным
резервированием? Объясните, почему банки могут работать в режиме частичного резервирования
вкладов. Если допустить, что центральный банк не регулирует размер обязательных
резервов, стремились бы коммерческие банки установить нулевой уровень своих
резервов?
Коммерческие банки держат часть
средств, внесенных вкладчиками на депозиты, на своем счету в центральном банке.
Резервы не приносят процентного дохода, но банк их держит по двум причинам:
часть как обязательные резервы (в соответствии с нормой резервирования), а
часть как дополнительные резервы наиболее ликвидных активов для совершения
обязательств при изъятии средств[4].
Обязательные резервы – это сумма денег, равная
определенному проценту собственных обязательств по вкладам коммерческого банка,
которую он должен держать либо в виде вклада в центральном банке, либо в виде
кассовой наличности. Их регулирование служит инструментом кредитно-денежной
политики центрального банка: при изменении нормативов резервных требований
изменяется денежная масса в обращении.
Величина, на
которую фактические резервы превышают обязательные резервы банка, составляет
избыточные резервы. От наличия избыточных резервов зависит способность
коммерческого банка предоставлять кредиты. Чем больше у банка избыточных
резервов, тем больше он может создать денег, принимая депозиты клиентов и
выдавая кредиты.
Нужно
заметить, что резервные требования являются частичными, что имеет большое
значение для кредитоспособности банка. При установлении нормы резервирования в
100% банк будет обязан резервировать все полученные денежные средства.
Соответственно, он не сможет эти деньги выдать в кредит и, следовательно,
получить проценты за его использование; также он не сможет приобрести
дополнительно ценные бумаги и получить доход по ним. Таким образом, ему будет
невыгодно принимать вклады, поскольку банк будет должен выплачивать проценты по
ним, но деньги не будут работать и приносить прибыль.
Банки могут работать в режиме
частичного резервирования, поскольку у них в этом случае будут существовать
избыточные резервы. Отдельный банк в состоянии одолжить такую сумму, которая
равна изначальным избыточным резервам, имевшимся у банка до момента выдачи
ссуды. Но ссуда системы коммерческих банков может в несколько раз превышать ее
избыточные резервы. Например, на чековый счет помещены 100 дол, что создает
исходный бессрочный вклад. При резервной норме в 20% для поддержания этого
депозита по закону требуется лишь 20 дол. Избыточные резервы в размере 80 дол.
позволяют банковской системе посредством выдачи ссуд создать бессрочные вклады
на 400 дол. Таким образом, 100 дол. обеспечивают 500 дол. денежной массы
(100дол.+400дол.) [5]
Это
достигается с помощью механизма денежного мультипликатора:
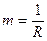, где R – норматив
резервных требований.
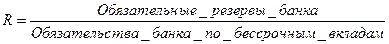
Величина денежного мультипликатора m показывает максимально возможное количество новых
денег в форме бессрочных депозитов, которое может быть создано одной единицей
избыточных резервов при данной величине R. Для определения максимального количества новых депозитных
денег D, которое может быть создано
банковской системой на основе любого данного объема избыточных резервов E, нужно умножить величину избыточных резервов на
денежный мультипликатор: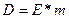 
Рассмотрим на числовом примере, как
банки создают деньги, используя избыточные резервы.
Пусть норматив резервных требований
равен 25%.
|
Активы,
млрд.дол.
|
Обязательства
и собственный капитал, млрд.дол.
|
|
Резервы 52
Ценные
бумаги 48
Ссуды 100
|
Бессрочные
депозиты 200
|
Здесь величина избыточных резервов = 52 млрд –
200млрд*25% = 2 млрд.дол. Максимальное количество денег, которые банковская
система может ссудить = (1/0,25)*2 млрд.дол.= 8
млрд.дол. Денежный мультипликатор равен 4 (1/0,25). Если резервная норма будет равна 20%, то это
увеличит избыточные резервы банковской системы с 2 млрд. дол. до 12 млрд.дол. и
денежный мультипликатор с 4 до 5. Этот пример
показывает, что чем меньше норма резервирования, тем больше ссуд могут выдать
банки и, тем самым, получить больший доход. Но установят ли банки нулевой
уровень резервов, если центральный банк перестанет регулировать размер
обязательных резервов? Рассмотрим этот вопрос ниже. Одна из главных проблем управления банком заключается в поддержании
оптимального соотношения между доходностью и риском. В банке должно быть
достаточно средств для выплаты вкладчикам в случае оттока депозитов. Для этого
в банке осуществляется управление риском ликвидности (он связан с
невозможностью быстрой конверсии финансовых активов в платежные средства без
потерь). Цель управления ликвидностью – застраховаться от потерь, связанных с
оттоком депозитов, путем создания избыточных резервов. При этом платой за
хранение избыточных резервов являются альтернативные издержки, равные доходам,
не полученным от потенциально возможного вложения в приносящие доход активы.
Отсюда ясно, что если центральный банк не будет регулировать размер обязательных
резервов, то коммерческий банк не установит нулевой уровень резервов.
Увеличивая ликвидность банка, резервы могут служить для привлечения клиентов как гарантия выплаты
вложенных средств[6].
Задача 4
Пусть
средняя норма резервирования вкладов равна 10%, норма предпочтения наличных
денег безналичным 20%. Определить, на сколько вырастет денежная масса, если
центральный банк предоставит кредит федеральному правительству в размере 40
млрд.рублей.
Решение: M=K/ (c+r), где М- денежная масса, c- норма предпочтения
наличных денег безналичным, r - норма резервирования, К – предоставленный кредит.
M= 40 млрд./(0,1+0,2)= 133,33 млрд.
Ответ:
денежная масса возрастет на 133, 33 млрд.рублей.
Список
литературы
1. В.М.Гальперин
и др. Микроэкономика. www. microeconomica. economicus.ru
2.
Э.Д. Долан. Р.Д.Кэмпбелл Деньги, банковское дело и денежно-кредитная
политика. М.; СПб., 1993. - 446с
3.
К.Р.Макконнелл, С.Л. Брю. Экономикс, том 1. М.,
Инфра-М,2000-456с.
4.
К.Р.Макконнелл, С.Л. Брю. Экономикс, том 2. М.,
Инфра-М,2000-528с.
5.
С.М.Пирожков и др.Деньги, финансовые рынки и
финансовые институты. Новосибирск, 2001 – 88с.
[1] К.Р.Макконнелл, С.Л. Брю. Экономикс, том 2. М., Инфра-М,2000 - стр.74-76, В.М.Гальперин
и др. Микроэкономика. www. microeconomica. economicus.ru глава 9.2.1
[2] К.Р.Макконнелл, С.Л. Брю. Экономикс, том 2. М., Инфра-М,2000- стр.77-81,
В.М.Гальперин
и др. Микроэкономика. www. microeconomica. economicus.ru глава 9.2.1
[3] К.Р.Макконнелл, С.Л. Брю. Экономикс, том 2. М., Инфра-М,2000- стр. 81-84,
В.М.Гальперин и др.
Микроэкономика. www. microeconomica.
economicus.ru глава 9.2.2
[4]К.Р.Макконнелл, С.Л. Брю. Экономикс, том 1. М., Инфра-М,2000-.
стр.298-306
С.М.Пирожков и
др.Деньги, финансовые рынки и финансовые институты. Новосибирск, 2001 –
стр.50-56 .
[5] К.Р.Макконнелл, С.Л. Брю. Экономикс, том 1. М., Инфра-М,2000-. стр.309-314
[6]С.М.Пирожков
и др.Деньги, финансовые рынки и финансовые институты. Новосибирск, 2001 – стр. 62-64