ЗАДАЧА 1 (сводка и группировка)

ЗАДАЧА 1 (сводка и группировка)

УСЛОВИЕ ЗАДАЧИ:

Известны данные по десяти крупнейшим рекламодателям в таблице 1.

Таблица 1

Исходные данные задачи 1

№ п/п	Фирма	Общие затраты на рекламу, млн. долл.	Общая сумма продаж, млн. долл.
1	Проктер энд гэмбл	641,7	11944
2	Сирс, Робак энд К ⁰	544,1	27360
3	Дженералс фудз	456,8	8351
4	Филипп Моррис	432,9	10885
5	Дженерал Моторс	401	62698
6	К- Март	349,6	16527
7	Набиско брэндз	340,9	5819
8	Р.Дж. Рейнолдзиндастриз	321,2	11691
9	АТТ	297	58214
10	Мобил	293,1	68587

1. Проранжируйте рекламодателей по удельным затратам на рекламу.

2. Выделите типические группы рекламодателей.

РЕШЕНИЕ:

1) Удельные затраты на рекламу определяются отношением общих затрат на рекламу к общей сумме продаж организации. Результаты расчетов удельным затрат представлены в таблице 2.

Таблица 2

Удельные затраты на рекламу

№ п/п	Фирма	Общие затраты на рекламу, млн. долл.	Общая сумма продаж, млн. долл.	Удельные затраты на рекламу
1	Проктер энд гэмбл	641,7	11944	0,0537
2	Сирс, Робак энд К ⁰	544,1	27360	0,0199
3	Дженералс фудз	456,8	8351	0,0547
4	Филипп Моррис	432,9	10885	0,0398
5	Дженерал Моторс	401	62698	0,0064
6	К- Март	349,6	16527	0,0212
7	Набиско брэндз	340,9	5819	0,0586
8	Р.Дж. Рейнолдзиндастриз	321,2	11691	0,0275
9	АТТ	297	58214	0,0051
10	Мобил	293,1	68587	0,0043

Проранжируем удельные затраты рекламодателей в порядке возрастания в таблице 3.

Таблица 3

Ранжированный ряд рекламодателей по удельным затратам на рекламу

№ п/п	Фирма	Общие затраты на рекламу, млн. долл.	Общая сумма продаж, млн. долл.	Удельные затраты на рекламу
1	Мобил	293,1	68587	0,0043
2	АТТ	297	58214	0,0051
3	Дженерал Моторс	401	62698	0,0064
4	Сирс, Робак энд К ⁰	544,1	27360	0,0199
5	К- Март	349,6	16527	0,0212
6	Р.Дж. Рейнолдзиндастриз	321,2	11691	0,0275
7	Филипп Моррис	432,9	10885	0,0398
8	Проктер энд гэмбл	641,7	11944	0,0537
9	Дженералс фудз	456,8	8351	0,0547
10	Набиско брэндз	340,9	5819	0,0586

2) Для выделения типических групп по общей сумме продаж определим величину интервала по формуле (1):

x_i = (x_max-x_min +1)/(1+3,322 lg10), (1)

x_i = (68587-5819+1)/(1+3,322 lg10) = 14523.

Выделяем интервалы и определяем количество фирм, попавших в эти интервалы в таблице 4

Таблица 4

5819-20342	6
20343-34866	1
34867-49390	0
49391-63914	2
63915-78438	1

Таким образом, наибольшее число фирм попало в первый интервал от 5819 до 20342 млн. руб.

ЗАДАЧА № 2 (ряды динамики)

УСЛОВИЕ ЗАДАЧИ:

Имеются данные о потерях рабочего времени на предприятии вследствие заболеваемости с временной утратой трудоспособности в таблице 5

Таблица 5

Исходные данные задачи № 2

Годы	Потери рабочего времени, дни
1	933,4
2	904,0
3	965,0
4	1014,1
5	1064,8
6	1122,9

1) Для определения тенденции проведите аналитическое выравнивание (подберите вид аналитической функции);

2) Отобразите фактические и теоретические (сглаженные) уровни ряда на графике. Покажите ожидаемые уровни ряда на следующие 2- 3 года, сделайте выводы.

РЕШЕНИЕ:

Для решения задачи нужно установить зависимость между годом и потерей рабочего времени. Для этого воспользуемся методом наименьших квадратов.

Имеем данные за 6 лет. Следовательно, имеем 6 экспериментальных значений точек с абсциссами

х₁, х₂, х₃, х₄, х₅ и х₆

и соответствующими ординатами

y₁, y₂, y₃, y₄, y₅ и y₆.

Зависимость y от x, задаваемая аналитической функцией

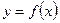(1)

не может совпадать с экспериментальными значениями во всех точках. Это означает, что для всех или некоторых точек разность

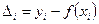(2)

будет отлична от нуля.

Требуется подобрать параметры функции (1) так, чтобы сумма квадратов разностей (2) была наименьшей, т.е. обратить в минимум выражение

(3)

По условию задачи исследовались потери рабочего времени в течение 6 лет. Поэтому имеются 6 различных значений параметра y (потери рабочего времени) 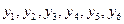и соответствующие им параметры x (номер исследуемого года).

Для определения неизвестных параметров a, b и с методом наименьших квадратов составим сумму квадратов отклонений искомой аналитической функции от наблюдаемых значений в данных точках

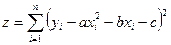(4)

Продифференцируем функцию (4) по неизвестным параметрам a, b, и с и приравняем производные к нулю. Получим систему уравнений:

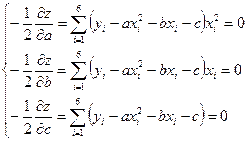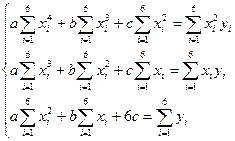или (5)

Перед решением полученной системы вычислим отдельно все суммы:

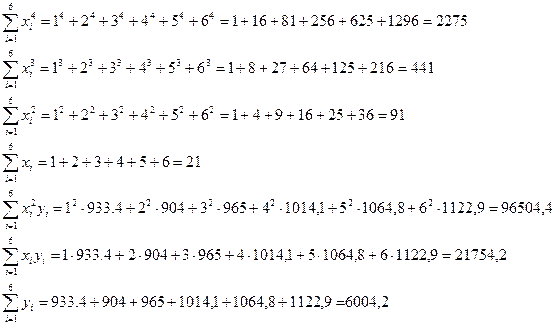
Теперь подставим найденные значения в (5), получим систему

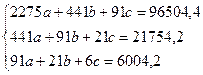
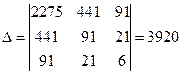
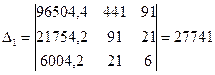
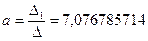
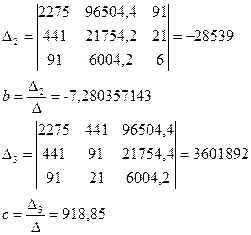
Получаем уравнение искомой аналитической функции:

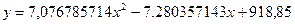
Используя полученную функцию, выполним расчет:

Год	Аналитические результаты	Фактические результаты
1	918,6464286	895,39
2	932,5964286	937,99
3	960,7	980,59
4	1002,957143	1023,19
5	1059,367857	1065,79
6	1129,932143	1108,39
7	1214,65	1150,99
8	1313,521429
9	1426,546429

Построим графики с изображением фактических и аналитических результатов

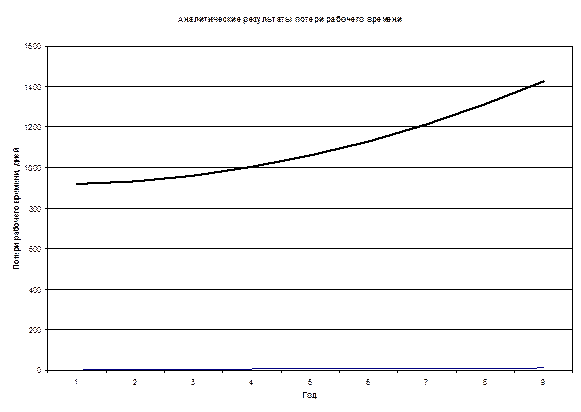
ЗАДАЧА № 3 (выборка)

УСЛОВИЕ ЗАДАЧИ:

Анализ 10 % банковских счетов, выделенных в результате бесповторного собственно-случайного отбора, показал следующее распределение, представленное в таблице 8.

Таблица 8

Исходные данные задачи № 3

Размер вклада, тыс. руб.	до 1	1-5	5-10	10-15	15 и более
Количество вкладов, %	20	25	40	10	5

Определите средний размер вклада, и, с вероятностью р = 0,954, установите его возможные пределы для всей совокупности вкладов населения.

РЕШЕНИЕ:

1) Для определения средней величины вклада интервального вариационного ряда сделаем переход от интервального ряда к дискретному, при котором за значение интервала принимается его середина. Результаты расчетов представлены в таблице 9.

Таблица 9

Расчет среднего размера вклада

размер вклада	количество вкладов	x_i	x_i-x₀	x_i-x₀/к	м'	(xi-x0/к)*м'
0-1	20	0,5	-9,5	-1,9	4	-7,6
1-5	25	3	-7	-1,4	5	-7
5-10	40	7,5	-2,5	-0,5	8	-4
10-15	10	12,5	2,5	0,5	2	1
15-20	5	17,5	7,5	1,5	1	1,5
Итого	100	не имеет смысла	не имеет смысла	не имеет смысла	20	-16,1

В качестве х₀ в таблице 9 взято условное начало, которое определяется по формуле (10):

х₀ = (х _мах + х _мин) /2, (10)

где х _мах = 0

х _мин = 20

Тогда х₀ = (0+20)/2 = 10.

Значение к есть величина интервала. Она равна 5.

Значение м’ определяется по формуле (11):

м’ = q / к, (11)

где q – количество вкладов

Далее определяем значение М по формуле (12):

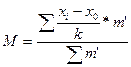, (12)

Подставляя значения в формулу (12), получим:

М = -16,1 /20 = -0,805

По формуле (13) определяем среднее значение вклада:

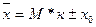, (13)

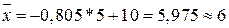
Таким образом, средний размер вклада примерно равен 6 тыс. руб.

2)Определим возможные пределы для всей совокупности вкладов с вероятностью р = 0,954.

При выборке объема n= 5, среднем значении 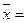6 и вероятности 0,954, определим значение среднего квадратического отклонения от средней σ по формуле (14):

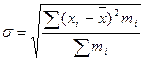, (14)

Таблица 10

x_i	m_i	x_i-x_ср	(x_i-x_ср)²	(x_i-x_ср)²*м_i
0,5	20	-5,48	29,98	599,5
3	25	-2,98	8,851	221,3
7,5	40	1,525	2,326	93,03
12,5	10	6,525	42,58	425,8
17,5	5	11,53	132,8	664,1
Итого	100	–	–	2004

Тогда,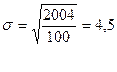

По таблице интегральной функции Лапласа находим, что:

Ф(t)=р /σ=0,954/4,5=0,212

Отсюда, t » 2.

Найдем значение среднеквадратичной ошибки Δ, которая для бесповторной выборки находится по формуле (15):

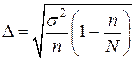, (15)

Здесь n=100, N=1000 (т.к. исследуем 10% банковских счетов), σ² = 4,5² =20,25.

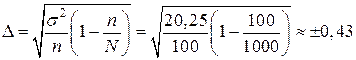
Возможные пределы для всей совокупности вкладов населения определим следующим образом:

(х_ср – Δ; х_ср + Δ), (16)

Подставляя имеющиеся значения в формулу (16), получим:

(6–0,43;6+0,43), т.е.

(5,57;6,43) тыс.руб.

ЗАДАЧА № 4 (взаимосвязи)

УСЛОВИЕ ЗАДАЧИ:

Установите, имеется ли взаимосвязь между показателями «Состав семьи» и «Успеваемость ребенка», используя критерий χ².

Таблица 11

Исходные данные задачи № 4

Состав семьи	Успеваемость ребенка в школе	Итого
неудовлетв.	удовлетвор.	хорошо	отлично
сирота	10	60	18	27	115
неполная семья	8	38	40	30	116
полная семья	3	26	40	38	107
всего	21	124	98	95	338

РЕШЕНИЕ:

Если указанные показатели являются зависимыми, то должно соблюдаться условие:

, (17)

где r = l-m-1,

m – количество параметров распределения, оцененных по выборке, оно равно 2.

l – количество интервалов, оно равно 4.

Тогда, r = 4-2-1 = 1.

m_i – фактическое попадание в интервал

n – объем выборки, он равен 338.

p_i – вероятность попадания каждого значения в интервал.

Для расчетов будем использовать данные таблицы 12 и 13.

Таблица 12

Расчет наблюдаемого значения критерия Пирсона для показателя «Успеваемость»

№ интервала Интервал	m_i	р_i	np_i	m_i-npi	(m_i-np_i)²	(m_i-np_i)²/np_i
1	21	21/338=0,062	1,3	19,7	388.09	298.530769
2	124	124/338=0,367	22,03	101,3	10261.69	465.805266
3	98	98/338=0,201	19,7	78,3	6130.89	311.21269
4	95	95/338=0,280	26,7	68,3	4664.89	174.714981
	338	1	69,73	267,6	21445.56	1250.26371

Таким образом, для показателя «Успеваемость» наблюдаемое значение критерия Пирсона равно 1250,26. Аналогичные расчеты проводим для значений показателя «Неполная семья».

Таблица 13

Расчет наблюдаемого значения критерия Пирсона для показателя «Неполная семья»

№ интервала	mi	р_i	np_i	m_i-np_i	(m_i-np_i)²	(m_i-np_i)²/np_i
1	115	115/338=0,34	39.1	75.9	5760.81	147.335294
2	116	116/338=0,34	39	75	5625	144.230769
3	107	107/338=0,32	33.87	73.13	5347.9969	157.897753
	338	1	111,97		16733.8069	449.4638165

Наблюдаемое значение критерия Пирсона равно 449,46.

ВЫВОДЫ: Можно видеть, что наблюдаемые значение критерия χ² для показателей «Состав семьи» и «Успеваемость ребенка» сильно отличаются друг от друга: 1250.26 и 449,46. Отсюда можно заключить, что эти два признака – «Состав семьи» и «Успеваемость ребенка» – независимы друг от друга.

ЗАДАЧА № 5 (индексы)

УСЛОВИЕ ЗАДАЧИ:

Имеются данные по предприятиям отрасли в таблице 14

Таблица 14

Исходные данные задачи № 5

Предприятие	Среднегодовая стоимость производственных фондов, тыс. руб.	Прибыль, тыс. руб.
предыдущий год	отчетный год	предыдущий год	отчетный год
1	9000	10800	1800	2000
2	6400	6800	1520	1640

Определите:

1) индексы рентабельности производства для каждого предприятия в отдельности (индивидуальные индексы);

2) индекс общего среднего уровня рентабельности производства (индекс переменного состава);

3) индекс общей рентабельности производства постоянного (фиксированного состава), поясните его отличие от индекса переменного состава.

РЕШЕНИЕ:

1) Рентабельность производства есть отношение прибыли к среднегодовой стоимости производственных фондов.

Индивидуальный индекс рентабельности производства рассчитывается как отношение рентабельности производства отчетного периода к предыдущему году по соответствующему предприятию.

Таблица 15

Рентабельности производства по предприятиям

Предприятие	Среднегодовая стоимость производственных фондов, тыс. руб.	Прибыль, тыс. руб.	Рентабельность, %
предыдущий год	отчетный год	предыдущий год	отчетный год	предыдущий год	отчетный год
С₀	С₁	П₀	П₁	Р₀=П₀/С₀	Р₁=П₁/С₁
1	9000	10800	9000	10800	20	18,52
2	6400	6800	6400	6800	23,75	24,12

Индивидуальные индексы:

- предприятие № 1: iр= 18,52/20=0,926

- предприятие № 2: iр = 24,12/23,75=1,016

Как видно, индивидуальный индекс по предприятию № 1 показывает, что рентабельность производства снизилась, по предприятию № 2 рентабельность производства выросла.

2) Индекс переменного состава определяется по формуле (17).

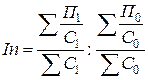, (17)

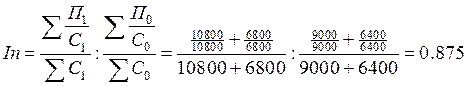
Таким образом, значение индекса переменного состава свидетельствует о снижении общего среднего уровня рентабельности производства на 22,5%.

2) Индекс постоянного состава определяем по формуле (18)

, (18)

Таким образом, индекс постоянного состава свидетельствует о росте значения общей рентабельности производства на 7 %.

Индекс постоянного состава в отличие от индекса переменного состава показывает влияние на показатель рентабельности изменения только значения стоимости производственных фондов.