1. Определить простую ставку процентов, при которой
первоначальный капитал в размере 10000 руб. достигнет через 180 дней суммы 13000,
Т=360 дней.
Решение.
13000=10000∙(1+180∙p/360), где p – искомая процентная ставка.
3000=1800000∙p/360
p=3000∙360/1800000
p=0.6
Следовательно, искомая процентная ставка – 60% годовых.
2. Кредит в размере 45000 выдан с 26.03 по 18.10 под простые
48% годовых. Определить размеры долга для различных вариантов начисления
процентов.
Решение.
«Английская практика»
tф=6+30+31+30+31+31+30+18–1=206
дней.
FV=PV+I
I=PV∙i∙(t/T),
где T – 360 дней.
I=45000∙0.48∙(206/360)=12360 руб.
FV=P+I=45000+12190.68=57190.68
руб.
«Французская практика»
tф=206
дней, T=360 дней.
I=45000∙0.48∙(206/360)=12360 руб.
FV=P+I=45000+12360=57360 руб.
«Германская практика»
tф=6+30+30+30+30+30+30+18–1=203
дней, T=360 дней.
I=45000∙0.48∙(203/360)=12180
руб.
FV=P+I=45000+12180=57180
руб.
3. Банк объявил следующие условия выдачи ссуды на год: за 1
квартал ссудный процент 48%, а в каждом последующем квартале процентная ставка
по ссуде увеличивается на 3%. Определить сумму к возврату в банк, если ссуда
выдана на год и составляет 45000 рублей (простые проценты).
Решение.
45000∙(1+(90∙0.48+91∙0.51+92∙0.54+
92∙0.57)/360) = 68966.25руб.
4. Договор вклада заключен на 8 лет и предусматривает
начисление и капитализацию процентов по полугодиям. Сумма вклада 45000 руб.,
годовая ставка 28%. Рассчитать сумму на счете клиента к концу срока.
Решение.
После первого полугодия сумма составит:
45000∙(1+0.14)=51300 руб.
Проведя аналогичное «начисление» 16 раз (по числу полугодий)
мы получим сумму:
45000∙(1+0.14)16 = 366176.22 руб.
5. Владелец векселя номинальной стоимости 13000 руб. и
сроком обращения 1 год предъявил его банку-эмитенту для учета за 60 дней до
платежа. Банк учел его по ставке 30%
годовых. Определить дисконтированную величину, то есть сумму, полученную
владельцем векселя и величину дисконта.
Решение.
Количество дней Т=360 дней, тогда дисконт.
D=13000∙0.3∙60/360
= 650 руб.
Дисконтированная величина.
13000–650=12350 руб.
6. Определить значение годовой учетной ставки банка,
эквивалентной ставке простых процентов 48% годовых (n=1).
Решение.
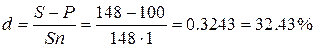
7. На вклады
ежеквартально начисляются проценты по номинальной годовой ставке 28%.
Определить сумму вклада для накопления через 1,5 года суммы 13000.
Решение.
Искомая сумма равна
= 
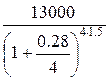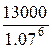= 8862.45 руб.
8. Банк предлагает долгосрочные кредиты под 48% годовых с
ежеквартальным начислением процентов, 50% годовых с полугодовым начислением
процентов и 44% с ежемесячным начислением процентов. Определить наиболее
выгодный для банка вариант кредитования.
Решение.
Рассчитаем сумму процентов за год на 1000 рублей кредита по
всем трем вариантам.
1. 
= 
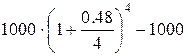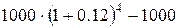= 573.52 руб.
2. 
= 
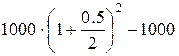= 562.5 руб.
3. 
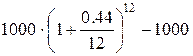= 540.53 руб.
Из приведенных расчетов видно, что наиболее выгодным для
банка будет первый вид кредитования.
9. Банк выдает кредит под 48% годовых. Полугодовой индекс
инфляции составил 0.09.
Определить реальную годовую ставку процентов с учетом инфляции.
Решение.
Искомая реальная ставка равна
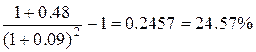
10. Какую ставку процентов по вкладам нужно назначить, чтобы
реальная доходность вклада с учетом инфляции 0.09 была 10% годовых.
Решение.
Воспользуемся формулой И. Фишера
iα=i+α+iα
Здесь iα – ставка с учетом инфляции
α –
уровень инфляции
i – ставка
процентов
Т. е. искомая ставка равна 0.1∙0.09+0.1+0.09=0.199 =
19.9%
11. Рассчитать уровень инфляции за год при ежемесячном
уровне инфляции 0.09.
Возьмем индекс инфляции за год.
In=(1+α)n=(1+0.09)12=2.81
Отсюда получаем:
In=1+αг→αг=In-1
αг= 2.81-1=1.81 = 181%
12. Вклад 45000 положен в банк на полгода с ежемесячным
начислением сложным начислением процентов по номинальной ставке 72% годовых.
Определить реальный доход вкладчика если ожидаемый ежемесячный уровень инфляции
составит 0.09.
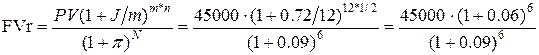= 32193.26 руб.
Реальный доход вкладчика
составит
32193.26–45000=–12806.74
13. Договор аренды имущества заключен на 5 лет. Аренда
уплачивается суммами S1=13000
руб., S2=14000
руб., S3=15000
руб. в конце 1го, 3го и 5го годов. По новому графику платежей вносятся две
суммы S4=16000
руб. в конце 2го года и S5
в конце 4 года. Ставка банковского процента 11%. Определить S5.
Решение.
Соотношение платежей в первом и втором вариантах выглядит
следующим образом
13000∙1.114+14000∙1.112+15000=
16∙1.113+S5∙1.11
19734.92+17249.4+15000=21882.1+S5∙1.11
1.11∙S5=30102.22
S5=27199.12
руб.
14. Определить размер ежегодных платежей по сложной ставке 11%
годовых для создания через 6 лет фонда в размере 13000000 руб.
Решение.
Обозначим искомую сумму N. Получим соотношение
N∙(1+1.11+1.112+1.113+1.114+1.115)
= 13000000
7.91286∙N=13000000
N=1642895.24
руб.
15. Рассчитать величину фонда, который может быть
сформирован за 2 года путем внесения в конце каждого года сумм 13000. Проценты
на вклад начисляются по ставке 11%.
Решение.
Искомая сумма = 13000∙(1.11+1)=27430 руб.
16. Ежемесячная средняя плата за квартиру составляет 3000
руб. Срок платежа – начало месяца. Рассчитать величину равноценного платежа,
взимаемого за год вперед. Ставка банковского депозита 48% годовых.
Решение.
Искомая сумма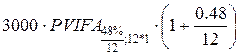 
=
3000∙9.385∙1.04 = 29281.2 руб.
17. Двухлетняя облигация номиналом 1000 руб. имеет 4
полугодовых купона доходностью 20% годовых каждый. Рассчитать цену ее
первоначального размещения, приняв ставку сравнения 11%.
Решение.
= 
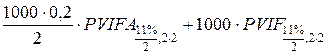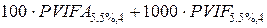= 100∙3.50515 + 1000∙0.807216 =
350.515+807.216 = 1157.73 руб.
18. Бескупонная облигация куплена по курсу 70 и продана по
курсу 88 через 90 дней. Рассчитать
доходность вложения по схеме сложных и простых процентов.
Решение.
Для сложных процентов:
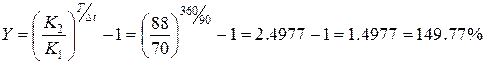
Для простых процентов:
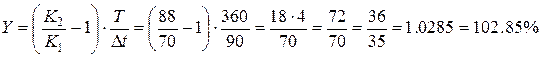
19. Представить план амортизации пятилетнего займа в 4500000
руб., погашаемого 1) равными суммами; 2) равными срочными уплатами. Процентная
ставка по займу 11%.
Решение.
1) Обозначим сумму долга после К года Dк, проценты –Iк.
У – величина срочной уплаты
У=const+Iк
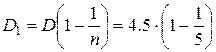= 3.6 млн. руб. – долг
после первого года.
I1=Dic=4.5∙0.11=0,495
млн. руб. – проценты
У1= Dic+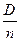
=0.495+0.9=1,395 млн. руб.
Второй год:
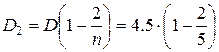=2,7 млн. руб
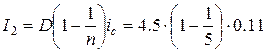= 0.396 млн. руб.
У2=0,396+0.9=1,296
Третий год
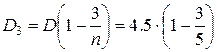=1,8 млн. руб
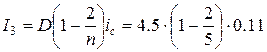= 0.297 млн. руб.
У3=0,297+0.9=1,197
Четвертый год
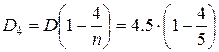=0,0 млн. руб
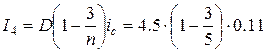= 0.198 млн. руб.
У3=0,198+0.9=1,098
Пятый год
D5=0
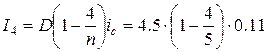= 0.099 млн. руб.
У5=0.099+0.9=0.999 млн. руб.
Сведем данные в таблицу:
|
Год
|
Уплата,
млн.
|
Проценты,
млн.
|
Долг,
млн. руб.
|
|
0
|
|
|
4.5
|
|
1
|
1.395
|
0.495
|
3.6
|
|
2
|
1.296
|
0.396
|
2.7
|
|
3
|
1.197
|
0.297
|
1.8
|
|
4
|
1.098
|
0.198
|
0.9
|
|
5
|
0.999
|
0.099
|
0
|
2) Периодическая выплата постоянной суммы У при заданной
процентной ставке ic в течении n лет является аннуитетом.
Величина срочной уплаты:
У=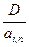
, где D – сумма долга, ai,n – коэффициент
приведения ренты.
ai,n=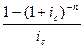
=
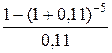= 3,7
Величина срочной уплаты:
У=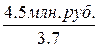 
= 1,2162 млн.руб.
Обозначим сумму платежа в конце k года через Pk, тогда:
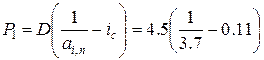= 0.7212 млн. руб.
I1=У-P1=1.2162–0.7212=0,495
млн. руб.
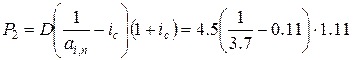= 0.8005 млн.руб.
I2=У-P2=1.2162–0.8005=0,4157
млн. руб.
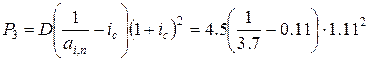= 0.8886 млн.руб.
I2=У-P2=1.2162–0.8886=0,3276
млн. руб.
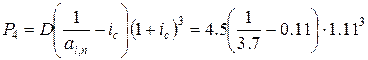= 0.9863 млн.руб.
I2=У-P2=1.2162–0.9863=0,2229
млн. руб.
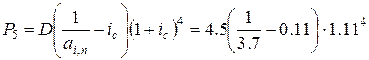= 1.0948 млн.руб.
I2=У-P2=1.2162–1.0948=0,1214
млн. руб.
Сведем данные в таблицу:
|
Год
|
Величина
срочной уплаты, млн. руб.
|
Сумма
платежа
|
Проценты
|
|
1
|
1.2162
|
0.7212
|
0.495
|
|
2
|
1.2162
|
0.8005
|
0.4157
|
|
3
|
1.2162
|
0.8886
|
0.3276
|
|
4
|
1.2162
|
0.9863
|
0.2229
|
|
5
|
1.2162
|
1.0948
|
0.1214
|