Вариант №6
Задача1
Вычислить 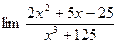 , если а)
, если а) 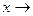 -5, б)
-5, б) 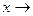 0, в)
0, в) 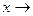
Решение:
Преобразуем данное выражение (в
знаменателе записали сумму кубов, в числителе вынесли за скобки (x+5)):
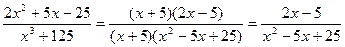
Преобразованное выражение не
имеет особенностей ни в точке x=-5, ни в x=0, поэтому для нахождения предела в этих точках просто
подставим x=-5 и x=0,
получим:
а) 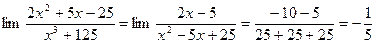
б) 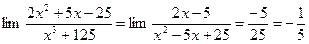
в) Для изучения поведения функции
на бесконечности преобразуем её следующим образом:
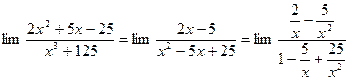
При 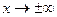 дроби
дроби 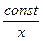 и
и 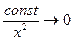 , а значит, выражение в числителе стремится к нулю (при
, а значит, выражение в числителе стремится к нулю (при 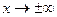 ), в знаменателе – к 1, предел всей дроби равен 0.
), в знаменателе – к 1, предел всей дроби равен 0.
Ответ: а) -0.2, б) -0.2, в) 0
Задача 2
Найти производные функций:
а) 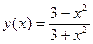 , вычислить
, вычислить 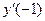
б) 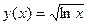
Решение:
а) Считаем производную дроби:
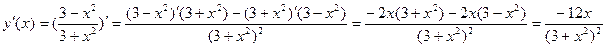
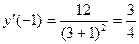
б) Считаем производную сложной
функции:
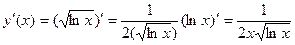
Ответ: а) 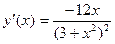 ,
, 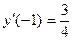 , б)
, б) 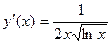
Задача 3
Составить уравнение касательной к
кривой y(x)=tgx в точке x0=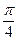
Решение:
Уравнение касательной к кривой y(x) в точке x=x0 имеет
вид: f(x)=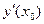 (x-x0)+у(x0)
(x-x0)+у(x0)
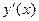 =
=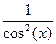 ,
, 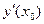 =2, y(x0)=1.
Таким образом, получаем окончательный ответ:
=2, y(x0)=1.
Таким образом, получаем окончательный ответ:
f(x)=2(x-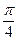 )+1
)+1
Задача 4
Точка движется по закону s(t)=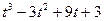 . Определить момент времени, когда её скорость будет 18 м/с.
. Определить момент времени, когда её скорость будет 18 м/с.
Решение:
Запишем выражение для скорости –
продифференцируем закон движения:
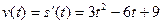
Пусть искомый момент времени t=t0. Тогда v(t0)=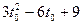 =18. Получаем
квадратное уравнение:
=18. Получаем
квадратное уравнение:
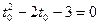 , D1=1-(-3)=4, t0=1+2=3 (отрицательный корень отбрасываем, т.к.
он не удовлетворяет условию задачи – время положительно).
, D1=1-(-3)=4, t0=1+2=3 (отрицательный корень отбрасываем, т.к.
он не удовлетворяет условию задачи – время положительно).
Ответ: t0=3.
Задача 5
Число 4 представьте в виде суммы
двух таких неотрицательных чисел, чтобы произведение их было наибольшим.
Решение:
Обозначим искомые два числа за х и у.
Тогда имеем:
х+у=4, а значит у=4-х.
Нам требуется найти максимум функции f(x)=-x2+4x – парабола, ветви
которой направлены вниз, значит, максимум существует и достигается при 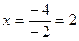 (координаты вершины
параболы). Следовательно, у=4-х=4-2=2.
(координаты вершины
параболы). Следовательно, у=4-х=4-2=2.
Ответ: х=2, у=2.
Задача 6
Исследовать функцию 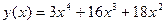 и построить её график.
и построить её график.
Решение:
Исследование функции начнём с
нахождения характерных точек: нулей функции, экстремальных точек и точек
перегиба.
Нули функции (приравниваем
функцию к нулю):
у(х)=0, 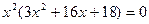 , х1,2=0,
, х1,2=0,
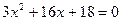 , D1=64-54=10,
, D1=64-54=10,
х3,4=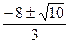
Экстремальные точки (приравниваем
производную к нулю):
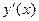 =
=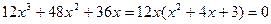 , х1=0, y(х1)=0,
, х1=0, y(х1)=0,
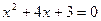 , D1=4-3=1,
, D1=4-3=1,
х2=-2+1=-1, х3=-2-1=-3, y(х2)=5, y(х3)=-27
Для определения характера
экстремальных точек необходимо изучить вторую производную:
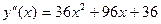
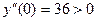 ,
, 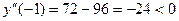 ,
, 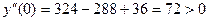 .
.
Таким образом, в точках x=0 и x=-3 функция достигает локального
минимума, в точке x=-1 – локального максимума.
Точки перегиба – нули второй
производной:
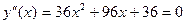 ,
,
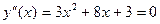 , D1=16-9=7,
, D1=16-9=7,
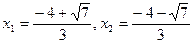 , y(х1)=2.32, y(х2)=-13.35
, y(х1)=2.32, y(х2)=-13.35
Поведение на бесконечности: при 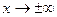
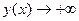
Анализируя полученные данные,
можем построить график функции:
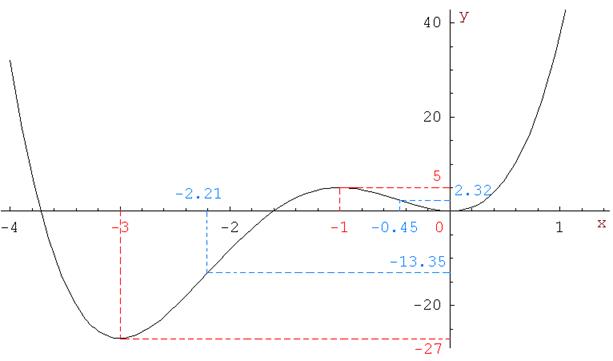
Комментарии: экстремальные точки
обозначены на графике красным цветом, точки перегиба – синим.