Всероссийский заочный финансово-экономический институт
Контрольная работа
По предмету: Экономико-математические методы и
прикладные модели
Выполнила:
Студентка 3 курса
Факультет: финансы и кредит
Вариант-8
Калуга 2008г.
1.8 Имеется два вида корма I
и II, содержащие питательные вещества (витамины S1 S2 и S3) Содержание числа единиц питательных веществ в
1 кг каждого вида корма и необходимый минимум питательных веществ приведены в
таблице.
|
Питательное
вещество
(витамин)
|
Необходимый
минимум питательных веществ
|
Число
единиц питательных веществ в 1 кг корма
|
|
I
|
II
|
|
S1
|
9
|
3
|
1
|
|
S2
|
8
|
1
|
2
|
|
S3
|
12
|
1
|
6
|
Стоимость
1 кг корма I и II
соответственно равны 4 и 6 ден.ед.
Необходимо
составить дневной рацион, имеющий минимальную стоимость, в котором содержание питательных веществ каждого вида
было бы не менее установленного предела.
Построить экономико-математическую
модель задачи, дать необходимые комментарии к её элементам и получить решение
графическим методом. Что произойдёт, если решить задачу на максимум, и почему?
Решение.
min f(x)= 4x1 + 6x2
3x1 + x2≥9
x1+2x2 ≥8
x1,x2≥0
по
скольку x1,x2≥0,то
решение задачи располагается в I четверти.
Рассмотрим уравнение 3x1 + x2≥9
x1 =0 => x2 =9
x2 =0 => x1= 3
Рассмотрим уравнение x1+2x2 ≥8
x1=0=> x2=4
x2=0=> x1=8
Рассмотрим уравнение x1 +6x2≥12
x1=0=> x2=2
x2=0=> x1=12
Построим
вектор, выходящий из начала координат в точку, соответствующую коэффициентам
при переменных целевой функции.
Опускаем
перпендикуляр.
Для
нахождения значения нулевой функции необходимо подставить найденное значение
целевой функции:
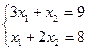
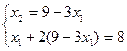
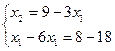
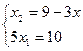
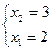
Подставим
удобрения х1=2, х2=3 в целевую функцию:
min F(x)= 4*2+6*3
min F(x) =20
Минимальная
стоимость дневного рациона, в котором содержание питательных веществ каждого
вила не менее установленного предела, равна 20 единиц.
По
скольку область определения функции бесконечна, то максимум функции найти
невозможно.
2.8
На основании информации, приведённой в таблице, решается задача оптимального
использования ресурсов на максимум выручки от реализации готовой продукции.
|
Тип сырья
|
Нормы расхода сырья на ед. продуции
|
Запасы сырья
|
|
I вид
|
II вид
|
III вид
|
|
I
II
III
|
1
3
1
|
2
0
4
|
1
2
0
|
430
460
420
|
|
Цена изделия
|
3
|
2
|
5
|
|
Требуется:
1.
Сформировать
прямую оптимизационную задачу на максимум выручки от реализации готовой
продукции, получить оптимальный план выпуска продукции.
2.
Сформулировать
двойственную задачу и найти её оптимальный план с помощью теорем
двойственности.
3.
Пояснить нулевые
значения переменных в оптимальном плане.
4.
На основе свойств
двойственной оценок и теорем двойственности:
·
Проанализировать
использование ресурсов в оптимальном плане исходной задачи;
·
Определить, как
изменяется выручка от реализации продукции и план её выпуска, если запас сырья I вида увеличить на 5 единиц, а II-уменьшить на 5 единиц;
·
Оценить
целесообразность включения в план изделия четвёртого вида ценой 7 у.е., если
нормы затрат сырья 2, 4 и 3 еденицы.
Решение.
Сформируем прямую
оптимизационную задачу.
Пусть x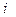 количество
продукции
количество
продукции  -го вида, тогда чтобы
максимизировать выручку от реализации готовой продукции, сформируем целевую
функцию.
-го вида, тогда чтобы
максимизировать выручку от реализации готовой продукции, сформируем целевую
функцию.
F(x)=3x1+2x2+5x3
=> max
x1+2x2+x3≤430
3x1+2x3≤460
x1+4x2≤420
x1…x3≥0
Будем считать, что решая
задачу симплекс методом, мы найдём оптимальный план.
Симплекс
метод.
Приведём
задачу к каноническому виду
F(x)=3x1+2x2+5x3+0x4+0x5+0x6
x1+2x2+x3+x4 = 430
3x1+2x3+x5 = 460
x1+4x2+x6 =
420
симплекс таблица:
Итерация
|
Базис
|
С
|
с
в
|
с1
|
с2
|
с3
|
с4
|
с5
|
с6
|
Q
|
3
|
2
|
5
|
0
|
0
|
0
|
0
|
А4
А5
А6
|
0
0
0
|
430
460
420
|
1
3
1
|
2
0
4
|
1
2
0
|
1
0
0
|
0
1
0
|
0
0
1
|
430
230
∞
|
|
|
|
|
-3
|
-2
|
-5
|
0
|
0
|
0
|
|
1
|
А4
А3
А6
|
0
5
0
|
200
230
420
|
-0,5
1,5
1
|
2
0
4
|
0
1
0
|
1
0
0
|
-0,5
0,5
0
|
0
0
1
|
100
∞
105
|
|
|
|
1150
|
4,5
|
-2
|
0
|
0
|
2,5
|
0
|
|
2
|
А2
А3
А6
|
2
5
0
|
100
230
20
|
-0,25
1,5
2
|
1
0
0
|
0
1
0
|
0,5
0
-2
|
-0,25
0,5
1
|
0
0
1
|
|
|
|
|
1350
|
4
|
0
|
0
|
0
|
2
|
0
|
|
Поскольку
поле приведения задачи к каноническому виду, матрица коэффициентов при
переменной в уравнениях ограничений, содержит единичную матрицу. Может быть
выделен первый опорный план:
Это
будет план - x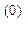 (0 0 0 430 460 420)
(0 0 0 430 460 420)
Целевая
функция f(x)=0
F(x)=3*0+2*0+5*0+0*430+0*460+0*420=0
В базис включены вектора А4,А5
,А6 , образующие единичную матрицу.
Рассчитаем
симплекс разности.
1 =Z1-C1
=Z1-C1
Z1= 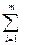 C*а
C*а
 1=0*1+0*3+0*1-3=
-3
1=0*1+0*3+0*1-3=
-3
 2=0*2+0*0+0*4-2=
-2
2=0*2+0*0+0*4-2=
-2
 3=0*1+0*2+0*0-5=
-5
3=0*1+0*2+0*0-5=
-5
 4=0
4=0
 5=0
5=0
 6=0
6=0
 Находим минимальный симплекс разности, это симплекс
разности- 3,
Находим минимальный симплекс разности, это симплекс
разности- 3,
Тем
самым будет введён вектор А3.
Определим
вектор который будет выведен из базиса, для этого рассчитаем отношение Q
Q1=430/1=430
Q2=460/2=230
Q3=420/0=∞
По
минимальному значению, из базиса выведен вектор А5
На пересечении направляющей
строки и направляющего столбца образовался элемент А2, 3=2
Приступим
к расчёту новых свободных членов и новых элементов матрицы А.
·
Свободные члены
-В
направляющей строке:
в’2= в2/а2
3=460/2=230
-В других строках:
в’1=в1*а2
3-в2*а13/а2 3=430*2-460*1/2=200
в’3 =в3 *а2
3-в2 *а33 /а2
3=420*2-460*0/2=420
·
Элементы матрицы
А
-В направляющей
строке:
а’21 =а21 /а23 =3/2=1,5
a’22=а22/а23
=0/2=0
a’23=а23/а23
=2/2=1
a’24=а24/а23
=0/2=0
a’25 =а25 /а23
=1/2=0,5
a’26=а26/а23
=0/2=0
-В других
строках:
а’11=а11*а2
3-а2*а13/а2 3=1*2-3*1/2=-0,5
а’12=
а12*а2 3-а22*а13/а2 3=2*2-0*1/2=2
а’13=
а1*а2 3-а23*а13/а2 3=0/2=0
а’14
= а1*а2 3-а24 *а13/а2 3=1*2-0*1/2=1
а’15=
а1*а2 3-а25*а13/а2 3=0*2-1*1/2=-0,5
а’16
= а1*а2 3-а26*а13/а2 3=0*2-0*1/2=0
а’31
= а31 *а2 3-а21*а33/а2 3=1*2-3*0/2=1
а’32=
а32*а2 3-а22*а33/а2 3=4*2-0*0/2=4
а’33=
а33*а2 3-а23*а33/а2 3=0/2=0
а’34=
а34*а2 3-а24 *а33/а2 3=0*2-0*0/2=0
а’35=
а35*а2 3-а25*а33/а2 3=0*2-0*1/2=0
а’36=
а36*а2 3-а26*а33/а2 3=1*2-0*0/2=1
Рассчитаем значение целевых функций
x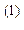 (0 0 230 200 0 420)
(0 0 230 200 0 420)
F(x)=3*0+2*0+5*230+0*200+0*0+0*420=1150
Рассчитаем
симплекс разности.
’ 1=0*0,5+5*1,5+0*1-3 = 4,5
1=0*0,5+5*1,5+0*1-3 = 4,5
’ 2=0*2+5*0+0*4-2
= -2
2=0*2+5*0+0*4-2
= -2
’ 3=0*0+5*1+0*0-5
= 0
3=0*0+5*1+0*0-5
= 0
’ 4=0*1+5*0+0*0-0
= 0
4=0*1+5*0+0*0-0
= 0
’ 5=0*(-0,5)+5*0,5+0*0-0=2,5
5=0*(-0,5)+5*0,5+0*0-0=2,5
 6=0*0+0*5+0*1-0=0
6=0*0+0*5+0*1-0=0
 Находим минимальный симплекс разности, это симплекс
разности- 2,
Находим минимальный симплекс разности, это симплекс
разности- 2,
Тем
самым будет введён вектор А2.
Определим вектор который будет выведен из базиса, для
этого рассчитаем отношение Q
Q1=200/2=100
Q2=230/0=∞
Q3=420/4=105
По
минимальному значению, из базиса выведен вектор А4
На пересечении направляющей
строки и направляющего столбца образовался элемент А1,2=2
Новый опорный план.
Приступим к расчёту свободных членов и новых
элемементов.
·
Новые свободные
члены
-в направляющей строке:
в’1= в1/а12=200/2=100
-В других строках:
в’2=в2*а12-в1*а22/а12=230*2-200*0/2=230
в’3 =в3 *а12-в1
*а32 /а12=420*2-200*4/2=20
·
Элементы матрицы
А
-В направляющей
строке:
а’11 =а11 /а12 =-0,5/2=-0,25
a’12=а12/а12
=2/2=1
a’13=а13/а12
=0/2=0
a’14=а14/а12
=1/2=0,5
a’15 =а15 /а12
=-0,5/2=-0,25
a’16=а16/а12
=0/2=0
-В других
строках:
а’21=а21*а12-а11*а22/а12=1,5*2-(-0,5)*0/2=-0,5
а’22=
а22*а12-а12*а22/а12=0/2=0
а’23=
а23*а12-а13*а22/а12=1*2-0*0/2=1
а’24
= а24*а12-а14 *а22/а12=0*2-0*1/2=0
а’25=
а25*а12-а15*а22/а12=0,5*2-0*(-0,5)/2=0,5
а’26
= а26*а12-а16*а22/а12=0*2-0*0/2=0
а’31
= а31 *а12-а11*а32/а12=1*2-(-0,5)*4/2=2
а’32=
а32*а12-а12*а32/а12=0/2=0
а’33=
а33*а12-а13*а32/а12=0*2-4*0/2=0
а’34=
а34*а12-а14 *а32/а12=0*2-4*1/2=-2
а’35=
а35*а12-а15*а32/а12=0*2-4*(-0,5)/2=1
а’36=
а36*а12-а16*а32/а12=1*2-4*0/2=1
Рассчитаем значение целевых функций
x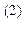 (0 100 230 0 0 20)
(0 100 230 0 0 20)
F(x)=3*0+2*100+5*230+0*0+0*0+0*20=1350
Подставим компоненты найденного оптимального плана в
сиситему функциональных задач.
F(х)=3*0+2*100+5*230=1350
0+2*100+230=430
3*0+2*230=460
0+4*100=400
y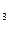 =0 по теореме 2(если
при подстановке компонент оптимального плана в систему ограничений исходной
задачи i-е ограничение исходной задачи обращается в
неравенство, i-е компонента оптимального плана
двойственной задачи обращается в ноль)
=0 по теореме 2(если
при подстановке компонент оптимального плана в систему ограничений исходной
задачи i-е ограничение исходной задачи обращается в
неравенство, i-е компонента оптимального плана
двойственной задачи обращается в ноль)
поскольку х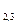 положительны, то по 2 теореме(если i-е компонента оптимального плана двойственной задачи
положительно, то i-е ограничение исходной задачи
превращается в строгое равенство)
положительны, то по 2 теореме(если i-е компонента оптимального плана двойственной задачи
положительно, то i-е ограничение исходной задачи
превращается в строгое равенство)
Сформируем двойственную задачу
Max f(x)= 3x1+2x2+5x3
Min u(x)=430y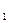 +460y
+460y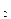 +420y
+420y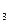
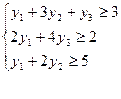
Решим
систему уравнений.
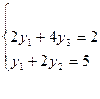
y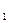 =1
=1
y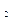 =2
=2
y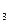 =0
=0
Подставим
в оптимальный план .
u(x)= 430*1+460*2+420*0=1350
Поскольку
Min u(x)= Max f(x, то можно
считать что задача решена.
3.8
Промышленная группа
предприятий(холдинг) выпускает продукцию трёх видов, при этом каждое из трёх
предприятий группы специализируется на выпуске продукции одного вида: первое
предприятие специализируется на выпуске продукции первого вида, второе
предприятие – продукции второго вида, третье предприятие – продукции третьего
вида. Часть выпускаемой продукции потребляется предприятиями холдинга (идёт внутреннее
потребление), остальная часть поставляется предприятиями холдинга (идёт на
внутреннее потребление), остальная часть поставляется за его пределы (внешним
потребителям, является конечным продуктом). Специалистам управляющей компании
получены экономические оценки а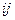 ( i=1, 2, 3; j=1, 2, 3) элементов технологической матрицы А ( норм
расхода, коэффициентов прямых материальных затрат) и элементов y вектора
конечной продукции Y.
( i=1, 2, 3; j=1, 2, 3) элементов технологической матрицы А ( норм
расхода, коэффициентов прямых материальных затрат) и элементов y вектора
конечной продукции Y.
Требуется:
1.
Проверить
продуктивность технологической матрицы А(а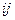 ) (матрицы коэффициентов прямых материальных затрат).
) (матрицы коэффициентов прямых материальных затрат).
2.
Построить баланс
(заполнить таблицу) производства и распределения продукции предприятия
холдинга.
|
Предприятия
(виды
продукции)
|
Коэффициенты
прямых затрат а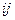
|
Конечный
продукт Y
|
|
1
|
2
|
3
|
|
1
2
3
|
0,0
0,4
0,3
|
0,4
0,1
0,0
|
0,1
0,0
0,1
|
160
180
150
|
Решение.
Сформируем
модель Леонтьева:
X1= X11+ X12+X13+ Y1
X2= X21
+ X22 + X23+ Y
2
X3= X31 + X32 + X33+ Y3
Следовательно:
X1= 0x1+0,4x2+0,1x3
+160
X2=0,4x1+0,1x2+0
x3+180
X3= 0,3 x1+0
x2+0,1x3+150
1 x1-0,4x2-0,1x3=160
-0,4 x1+0,9
x2-0 x3=180
-0,3 x1-0
x2+0,9 x2=150
1
-0,4 -0,1
А= -0,4 0,9 0
-0,3 0 0,9
 160
160
В= 180
150
X1
X= X2
X3

 1 -0,4
-0,1 1*0,9*0,9+(-0,4)*0*0,3+(-0,4)*0*(-0,1)-(-0,1)*
1 -0,4
-0,1 1*0,9*0,9+(-0,4)*0*0,3+(-0,4)*0*(-0,1)-(-0,1)*
 = -0,4 0,9
0 = *0,9*(-0,3)-(-0,4)*(-0,4)*0,9-0*0*1=0,639
= -0,4 0,9
0 = *0,9*(-0,3)-(-0,4)*(-0,4)*0,9-0*0*1=0,639
-0,3 0 0,9

 160 -0,4 -0,1 160*0,9*0,9+(-0,4)*0*150+180*0*(-0,1)-
160 -0,4 -0,1 160*0,9*0,9+(-0,4)*0*150+180*0*(-0,1)-
 1= 180
0,9
0 = -(-0,1)*0,9*150-180*(-0,4)*0,9-0*0*160=
1= 180
0,9
0 = -(-0,1)*0,9*150-180*(-0,4)*0,9-0*0*160=
150 0
0,9 =207,9

 1
160 -0,1 1*180*0,9+160*0*(-0,3)+(-0,4)*150*(-0,1)-
1
160 -0,1 1*180*0,9+160*0*(-0,3)+(-0,4)*150*(-0,1)-
 2= -0,4
180 0 = -(-0,1)*180*(-0,3)-(-0,4)*160*0,9-150*0*1=
2= -0,4
180 0 = -(-0,1)*180*(-0,3)-(-0,4)*160*0,9-150*0*1=
-0,3 150 0,9 =220,2

 1 -0,4 160 1*0,9*150+(-0,4)*180*(-0,3)+(-0,4)*0*160-
1 -0,4 160 1*0,9*150+(-0,4)*180*(-0,3)+(-0,4)*0*160-
3 = -0,4
0,9 180 = -160*0,9*(-0,3)-(-0,4)*(-0,4)*150-180*0*1=
= -0,4
0,9 180 = -160*0,9*(-0,3)-(-0,4)*(-0,4)*150-180*0*1=
-0,3 0 150 =175,8

 X1= 1
/ = 207,9/0,639=325,35
X1= 1
/ = 207,9/0,639=325,35

 X2= 2 /
= 220,2/0,639=344,6
X2= 2 /
= 220,2/0,639=344,6

 X3= 3/ =
175,8/0,639=375,12
X3= 3/ =
175,8/0,639=375,12
Проверка:
325,5-0,4*344,6-0,1*275,12=160
(верно)
-0,4*325,35+0,9*344,6-0*275,12=180
(верно)
-0,3*325,35-0*344,6+0,9*275,12=150
(верно)
Сформируем элементы, которые
и будут составлять баланс производства и распределения продукции предприятий
холдинга.
x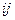 =X
=X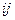 *a
*a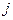

x11= X1*а11=325,5*0=0
x12= X2*а12=344,6*0,4=137,84
x13= X3*а13=275,12*0,1=27,512
x21= X1*а21=325,5*04=130,14
x22= X2*а22=344,6*0,1=34,46
x23= X3*а23=275,12*0=0
x31= X1*а31=325,5*0,3=97,605
x32= X2*а32=344,6*0=0
x33= X3*а33=275,12*0,1=27,512
Заполним баланс:
|
Потреб.
Произв.
|
1
|
2
|
3
|
Коэффициент
продукции Y
|
Валовая продукция X
|
|
1
|
0
|
137,84
|
27,512
|
160
|
325,35
|
|
2
|
130,14
|
34,46
|
0
|
180
|
344,6
|
|
3
|
97,605
|
0
|
27,512
|
150
|
275,12
|
|
|
227,745
|
172,3
|
55,024
|
490
|
945,07
|
4.8
В течении девяти последовательных недель фиксировался спрос Y(t)
(млн.
руб.) на кредитные ресурсы финансовой компании.
Требуется:
1.
Проверить наличие
аномальных наблюдений.
2.
Построить
линейную модель 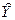 (t)=а
(t)=а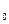 +а1к, параметры которой оценить МНК (
+а1к, параметры которой оценить МНК (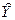 (t) – расчётные, смоделированные
значения временного ряда).
(t) – расчётные, смоделированные
значения временного ряда).
3.
Построить
адаптивную модель Брауна 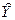 (t)=а
(t)=а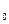 +а1к с параметром сглаживания
+а1к с параметром сглаживания 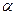 = 0,4;
= 0,4; 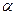 = 0,7; выбрать лучшее значение параметра сглаживания.
= 0,7; выбрать лучшее значение параметра сглаживания.
4.
Оценить
адекватность построенных моделей, используя свойства независимости остаточной
компоненты, случайности и соответствия нормальному закону распределения (при
использовании R/S-критерия взять табулированные границы 2,7-3,7).
5.
Оценить точность
моделей на основе использования средней относительной ошибки аппроксимации.
6.
Фактические
значения показателя, результаты моделирования и прогнозирования представить
графически.
Решение.
8
13
15
19
25
27
33
35
40
Расчёт параметров моделей с помощью наименьших
квадратов.
а1=
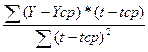
Ycp=8+13+15+19+25/5=16
tcp=1+2+3+4+5/5=3
а1=(8-16)*(1-3)+(13-16)*(2-3)+(15-16)*(3-3)+(19-16)*(4-3)+(25-16)*(5-3)/(1-3)
2 +(2-3) 2 +(3-3) 2 +(4-3) 2 +(5-3)
2 =4

а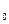 =Ycp- а1*tcp
=Ycp- а1*tcp
а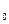 =16-4*3=4
=16-4*3=4
Сформулируем
адаптивную модель
Yр(t, k)= а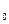 (t, k)+ а1(t, k)*t
(t, k)+ а1(t, k)*t
Yр(t, k)=4+4*t
Рассчитаем
модель Брауна при 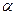 =0,4:
=0,4:
|
Шаг
|
Y(t)
|
Yp(t)
|
а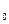
|
а1
|
E(t)
|
|
0
1
2
3
4
5
6
7
8
9
|
8
13
15
19
25
27
33
35
40
|
8
16
22,08
23,47
23,93
28,46
30,3
37,41
37,67
|
4
8
3,52
2,39
1,67
1,84
1,61
2,042
1,66
2,03
|
4
4
11,52
13,91
15,58
17,42
19,03
21,072
22,73
24,77
|
0
-3
-7,08
-4,47
1,07
-1,46
2,7
-2,41
2,33
|
·
Yp1=a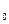 (0)+ а1(0)*t
(0)+ а1(0)*t
Yp1=4+4*1=8
e1= Y 1- Yp1
e1=8-8=0
a1 (1)= а1(0)+ 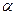 2* e1
2* e1
a1 (1)=4+0,42*0=4
a0 (1)= a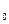 (0)+а1(0)+
(0)+а1(0)+ 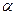 2* e1
2* e1
a0 (1)= 4+4+0,42*0=8
·
Yp2=8+4*2=16
e2=13-16=-3
a1 (2)=4+0,42*(-3)=3,52
a0 (2)= 8+4+0,42*(-3)=11,52
·
Yp3=11,52+3,52*3=22,08
e3=15-22,08=-7,08
a1 (3)=3,52+0,42*(-7,08)=2,39
a0 (3)= 11,52+3,52+0,42*(-7,08)=13,91
·
Yp4=13,91+2,39*4=23,47
е4=19-23,47=-4,47
a1 (4)=2,39+0,42*(-4,47)=1,67
a0 (4)= 13,91+2,39+0,42*(-4,47)=15,58
·
Yp5=15,58+1,67*5=23,93
е5=25-23,93=1,07
a1 (5)=1,67+0,42*1,07=1,84
a0 (5)= 15,58+1,67+0,42*1,07=17,42
·
Yp6=17,42+1,84*6=28,46
е6=27-28,46=-1,46
a1 (6)=1,84+0,42*(-1,46)=1,61
a0 (6)= 17,42+1,84+0,42*(-1,46)=19,03
·
Yp7=19,03+1,61*7=30,3
е7=33-30,3=2,7
a1 (7)=1,61+0,42*2,7=2,042
a0 (7)= 19,03+1,61+0,42*2,7=21,072
·
Yp8=21,072+2,042*8=37,41
е8=35-37,41=-2,41
a1 (8)=2,042+0,42*(-2,41)=1,66
a0 (8)= 21,072+2,042+0,42*(-2,41)=22,73
·
Yp9=22,73+1,66*9=37,67
е9=40-37,67=2,33
a1 (9)=1,66+0,42*2,33=2,03
a0 (9)= 22,73+1,66+0,42*2,33=24,77
1.
Оцениваем на адекватность
по критериям квадратных точек.
 q=int
q=int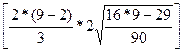 =int(4,7-2,26)
=int(4,7-2,26)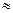 2,24
2,24
проверяем на случайность.
d=
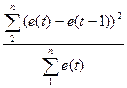
d=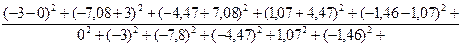
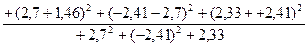
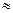 1,34
1,34
0,95<1,34<2, значение
ряда остатков подчиняется единому закону независимости.
Оцениваем на точность
E(t)
|
Y(t)
|
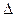 E(t) E(t)
|
|
|
0
-3
-7,08
-4,47
1,07
-1,46
2,7
-2,41
2,33
|
8
13
15
19
25
27
33
35
40
|
0
-0,23
-0,47
-0,23
0,04
-0,05
0,08
-0,09
0,06
|
-
0
1
0
1
1
1
1
-
|
7-поворотных точек
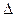 E(t)= E(t)/ Y(t)
E(t)= E(t)/ Y(t)
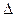 E1=0/8=0
E1=0/8=0
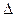 E2=-3/13=-0,23
E2=-3/13=-0,23
 E3=-7,08/15=-0,47
E3=-7,08/15=-0,47
 E4=-4,47/19=-0,23
E4=-4,47/19=-0,23
 E5=1,07/25=0,04
E5=1,07/25=0,04
 E6=-1,46/27=-0,05
E6=-1,46/27=-0,05
 E7=2,7/33=0,08
E7=2,7/33=0,08
 E8=-2,41/25=-0,09
E8=-2,41/25=-0,09
 E9=2,33/40=0,06
E9=2,33/40=0,06
 Eм=
Eм=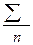 *100%
*100%
 Eм=
Eм=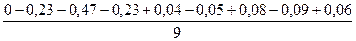 *100%=-9,9
*100%=-9,9
Рассчитаем
модель Брауна при 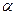 =0,7:
=0,7:
|
Шаг
|
Y(t)
|
Yp(t)
|
а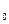
|
а1
|
E(t)
|
|
0
1
2
3
4
5
6
7
8
9
|
8
13
15
19
25
27
33
35
40
|
8
16
18,12
15,54
27,73
23,76
39,19
17,79
101,6
|
4
8
10,53
11,53
14,23
15,59
18,54
18,46
26,8
4,83
|
4
4
2,53
1,0012
2,7
1,362
2,95
-0,0831
8,34
21,97
|
0
-3
-3,12
3,464
-2,73
3,24
-6,19
17,2
-61,86
|
·
Yp1=4+4*1=8
e1=8-8=0
a1 (1)=4+0,72*0=4
a0 (1)= 4+4+0,42*0=8
·
Yp2=8+4*2=16
e2=13-16=-3
a1 (2)=4+0,72*(-3)=2,53
a0 (2)= 8+4+0,72*(-3)=10,53
·
Yp3=10,53+2,53*3=18,12
e3=15-18,12=-3,12
a1 (3)=2,53+0,72*(-3,12)=1,0012
a0 (3)= 10,53+2,53+0,72*(-3,12)=11,5312
·
Yp4=11,5312+1,0012*4=15,54
е4=19-15,54=3,464
a1 (4)=1,0012+0,72*3,464=2,7
a0 (4)= 11,5312+1,0012+0,72*3,464=14,23
·
Yp5=14,23+2,7*5=27,73
е5=25-27,73=-2,73
a1 (5)=2,7+0,72*(-2,73)=1,362
a0 (5)= 14,23+2,7+0,72*(-2,73)=15,59
·
Yp6=15,59+1,362*6=23,76
е6=27-23,76=3,24
a1 (6)=1,362+0,72*(3,24)=2,95
a0 (6)= 15,59+1,362+0,72*(3,24)=18,54
·
Yp7=18,54+2,95*7=39,19
е7=33-39,19=-6,19
a1 (7)=2,95+0,72*(-6,19)=-0,0831
a0 (7)= 18,54+2,95+0,72*(-6,19)=18,46
·
Yp8=18,46+(-0,0831)*8=17,79
е8=35-17,79=17,2
a1 (8)=-0,0831+0,72*17,2=8,34
a0 (8)= 18,46+(-0,0831)+0,72*17,2=26,8
·
Yp9=26,8+8,34*9=101,86
е9=40-101,86=-61,86
a1 (9)=8,34+0,72*(-61,86)=-21,97
a0 (9)= 26,8+8,34+0,72*(-61,86)=4,83
2.
Оцениваем на
адекватность по критериям квадратных точек.
 q=int
q=int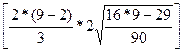 =int(4,7-2,26)
=int(4,7-2,26)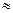 2,24
2,24
проверяем на случайность.
d=
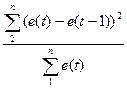
d=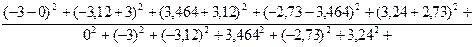
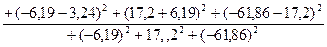
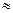 1,67
1,67
1,54<1,67<2, значение
ряда остатков подчиняется единому закону независимости.
проверка уровня рядов
остатков.
h=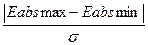
3.
Оцениваем на
точность
E(t)
|
Y(t)
|
 E(t) E(t)
|
|
|
0
-3
-3,12
3,464
-2,73
3,24
-6,19
17,2
-61,86
|
8
13
15
19
25
27
33
35
40
|
0
-0,23
-0,208
0,18
-0,11
0,12
-0,19
0,5
-1,55
|
-
1
0
1
1
1
1
1
-
|
8-поворотных точек
 E(t)= E(t)/ Y(t)
E(t)= E(t)/ Y(t)
 E1=0/8=0
E1=0/8=0
 E2=-3/13=-0,23
E2=-3/13=-0,23
 E3=-3,12/15=-0,208
E3=-3,12/15=-0,208
 E4=3,464/19=0,18
E4=3,464/19=0,18
 E5=-2,73/25=-0,11
E5=-2,73/25=-0,11
 E6=3,24/27=0,12
E6=3,24/27=0,12
 E7=-6,19/33=-0,19
E7=-6,19/33=-0,19
 E8=17,2/35=0,5
E8=17,2/35=0,5
 E9=-61,86/40=-1,55
E9=-61,86/40=-1,55
 Eм=
Eм=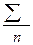 *100%
*100%
 Eм=
Eм=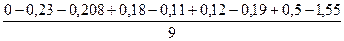 *100%=-16,5
*100%=-16,5
Всероссийский заочный финансово-экономический институт
Контрольная работа
По предмету: Экономико-математические методы и
прикладные модели
Выполнила:
Студентка 3 курса
Факультет: финансы и кредит
Норка Ю.В.
Проверила:
Князева И.В.
Вариант-8
Калуга 2008г.