Задача 1
1) Дайте понятие
производственной функции и изокванты. Что означает взаимозаменяемость ресурсов.
Ответ:
Производственной функцией называется зависимость количества продукта, которое может произвести
фирма, от объемов затрат ресурсов. Производственная функция характеризует чисто техническую зависимость
между количеством применяемых ресурсов и объемом выпускаемой продукции в
единицу времени. Производственная функция описывает множество технически
эффективных способов производства заданного объема продукции.
Изокванта (в теории
производственных функций) – это геометрическое место точек в пространстве
ресурсов, в которых различные сочетания производственных ресурсов дают одно и
то же количество выпускаемой продукции.
Взаимозаменяемость
ресурсов - это возможность использования разных видов ресурсов для достижения
народно-хозяйственного оптимума. Различают взаимозаменяемость ресурсов
техническую и экономическую. Разработаны экономико-математические модели
расчетов эффективности взаимной замены ресурсов.
2) Производственная
функция для райпо имеет вид 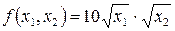 , где
, где 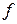 - товарооборот;
- товарооборот; 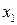 - производственная площадь;
- производственная площадь; 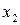 - численность
работников. Рассмотрите изокванту уровня
- численность
работников. Рассмотрите изокванту уровня 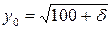 и найдите на ней точку
C1 с координатами
и найдите на ней точку
C1 с координатами 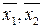 , где
, где 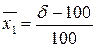 , и точку С2 с координатами
, и точку С2 с координатами 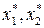 , где
, где 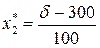 . Сделайте вывод о возможности замены ресурсов (
. Сделайте вывод о возможности замены ресурсов ( ) и (
) и (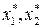 ). Полученные
результаты изобразите графически.
). Полученные
результаты изобразите графически.
Решение:
Уравнение изокванты при 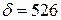 имеет вид:
имеет вид:
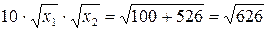
Возводя обе части в квадрат и поделив
их на 100, получим:
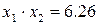
Найдем координаты точки С1:
Так как 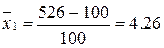 , то из уравнение изокванты находим
, то из уравнение изокванты находим 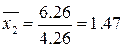
Аналогично находим координаты точки С2. Так как 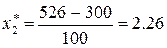 , то
, то 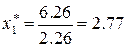
Итак, 147 работников
райпо, используя 4,26 тыс. кв. м. производственной площади, обеспечат
товарооборот 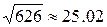 (млн. руб.), и такой же товарооборот могут обеспечить 226
работников райпо, используя площадь 2,77 тыс. кв. м.
(млн. руб.), и такой же товарооборот могут обеспечить 226
работников райпо, используя площадь 2,77 тыс. кв. м.

Задача
4
1) Объясните смысл элементов
платежной таблицы и способы выбора стратегии с позиций крайнего пессимизма,
крайнего оптимизма и оптимизма-пессимизма.
Ответ:
Таблица, состоящая из m строк и n столбцов элементами которой являются
выигрыши, соответствующие стратегиям Аi и ej, называется платежной матрицей.
Обозначим через ai наименьший выигрыш игрока А при
выборе им стратегии Аi для всех возможных стратегий игрока e (наименьшее
число в i-той строке платежной таблицы). Среди всех чисел ai выберем наибольшее a. Стратегия, соответствующая a, называется стратегией крайнего пессимизма.
Игрок e заинтересован в том, чтобы уменьшить
выигрыш игрока А. Выбирая стратегию bj, он учитывает максимально возможный
выигрыш для А (наибольшее число в j-том столбце платежной таблицы).Среди
всех чисел bj выберем наименьшее b. Стратегия, соответствующая b, называется стратегией крайнего оптимизма.
Принцип, диктующий
игрокам выбор наиболее осторожных стратегий называется стратегией
оптимизма-пессимизма.
2) Выберете стратегии с
позиции крайнего пессимизма, крайнего оптимизма и оптимизма-пессимизма для
следующей платежной таблицы. Укажите соответствующие выигрыши:
|
e
А
|
e 1
|
e 2
|
e 3
|
|
А1
|
d-490
|
d-480
|
620-d
|
|
А2
|
610-d
|
620-d
|
630-d
|
|
А3
|
|550-d|+10
|
|560-d|+10
|
640-d
|
Решение:
Для числа d = 526 таблица приобретает вид:
|
e
А
|
e 1
|
e 2
|
e 3
|
|
А1
|
36
|
46
|
94
|
|
А2
|
84
|
94
|
84
|
|
А3
|
34
|
44
|
74
|
Выберем по каждой строке таблицы
минимальное из чисел ai, максимальное bi, а затем вычислим их полусумму gi.
|
e
А
|
e 1
|
e 2
|
e 3
|
ai
|
bi
|
gi
|
|
А1
|
36
|
46
|
94
|
36
|
94
|
65
|
|
А2
|
84
|
94
|
104
|
84
|
104
|
94
|
|
А3
|
34
|
44
|
114
|
34
|
114
|
74
|
Получим:
a =
max(a1, a2, a3) = max(36, 84, 34) = 84;
b = max(b1, b2, b3) = max(94, 104, 114) = 114;
g = max(g1, g2, g3) = max (65, 94, 74) = 94.
Так как a = 84, и это
число находится в строке, соответствующей А2, то А2 –
стратегия крайнего пессимизма, ожидаемый выигрыш равен 84 единицам. Так как b = 114, и это число находится в
строке, соответствующей А3, то А3 – стратегия крайнего
оптимизма, ожидаемый выигрыш равен 114 единицам. Так как g = 94, и это
число находится в строке, соответствующей А2, то А2 –
стратегия оптимизма - пессимизма, ожидаемый выигрыш равен 94 единицам.
Задание
5
1) Дайте описание
входящего потока требований и каналов обслуживания. Какие экономические
показатели характеризуют работу СМО.
Ответ:
Основными элементами СМО
являются: входящий поток требований, очередь требований, обслуживающие
устройства, (каналы) и выходящий поток требований. Входящий поток требований
представляет собой совокупность требований, которые поступают в систему и
нуждаются в обслуживании. Входящий поток требований изучается с целью
установления закономерностей этого потока и дальнейшего улучшения качества
обслуживания. Средства,
обслуживающие требования, называются обслуживающими устройствами или каналами
обслуживания.
Следующие экономические показатели характеризуют работу СМО:
среднее число требований в очереди на обслуживание, среднее число требований,
находящихся в системе (на обслуживании и в очереди), среднее число каналов,
простаивающих из-за отсутствия работы, коэффициент простоя обслуживаемо объекта
в очереди, коэффициент использования объектов, коэффициент простоя
обслуживающих каналов, среднее время ожидания обслуживания ( время ожидания
обслуживания в очереди)
2) В магазине
самообслуживания работают две кассы с интенсивностью m=(d+300)/100 (треб./мин.) каждая.
Входящий поток требований имеет интенсивность l= (d+400)/100 (). Рассчитайте долю
времени простоя касс и среднюю длину очереди. Если интенсивность входящего
потока станет равной l= (700-d/10 (треб./мин.), то будет ли
выполнено условие стационарности? Если будет, то во сколько раз увеличится
средняя длина очереди?
Решение:
Пусть d=526, тогда m=8,26 (треб./мин.), а первоначальное
значение l=9,26 (треб./мин.).
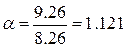
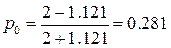 (
(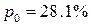 )
)
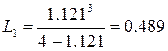 (треб.)
(треб.)
Если интенсивность l станет равной 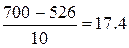 , то в силу неравенства
, то в силу неравенства 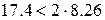 условие стационарности
СМО выполнено и можно вычислить среднюю длину очереди:
условие стационарности
СМО выполнено и можно вычислить среднюю длину очереди:

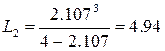 ( треб.)
( треб.) 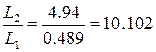
Итак, при интенсивности
обслуживания m=8,26 (треб./мин.) и интенсивности
входа l=9,26 (треб./мин.), доля времени
простоя касс составляет 28,1% времени, а средняя длина очереди равна 0,489
(треб.). Если же интенсивность входа станет равной 17,4 (треб./мин.), то
средняя длина очереди увеличится в 10,102 раза.
Задание
6
1) Сформулируйте задачу
оптимального управления запасами.
Ответ:
Задача оптимального
управления запасами состоит в отыскании такой стратегии пополнения и расхода
запасами, при котором функция затрат
принимает минимальное значение.
2) Дайте экономическую
интерпретацию предельной арендой платы.
3) Сделайте вывод о
целесообразности аренды дополнительных складских емкостей или о необходимости
сокращения объема заказываемой партии товара с учетом имеющихся складских
емкостей при сравнении фактической a (руб./кг*сут.) и предельной l (руб./кг*сут.) арендной платы за хранение единицы
товара в единицу времени.
a = 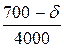 l =
l = 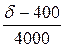
Решение:
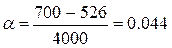 (руб./кг*сут.)
(руб./кг*сут.)
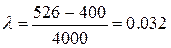 (руб./кг*сут.)
(руб./кг*сут.)
Вывод:
Фактическая арендная
плата больше предельной арендной платы. Следовательно, аренда дополнительных
складских емкостей невыгодна, и тогда объем заказываемой партии надо сократить
до таких пределов, чтобы возникший товарный запас можно было разместить в
имеющихся складских емкостях.
Задание
7
1)
Дайте понятие генеральной и выборочной совокупностей.
Ответ:
Генеральной совокупностью
называется исследуемая совокупность объектов. Совокупность m объектов, отобранных случайным
образом из генеральной совокупности, называется выборочной совокупностью.
2)
Определите соотношение между доверительными интервалами:
а) при фиксированных
значениях среднеквадратического отклонения s, надежности P и различных значениях объема выборки

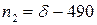
б) при фиксированных
значениях среднеквадратического отклонения s, объема выборки n и различных значениях надежности

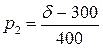
в) при фиксированных
значениях надежности P, объема выборки n и различных значениях
среднеквадратического отклонения

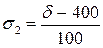
Решение:
а) 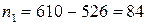
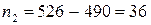
Объемы выборок
находятся в соотношении 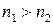 . Тогда из формулы нахождения погрешности
. Тогда из формулы нахождения погрешности
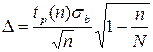
 (7.1)
(7.1)
следует, что при
возрастании объема выборки n значение D уменьшается и 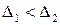 , т.е. доверительный интервал, соответствующий объему выборки
n1 = 84, будет меньше доверительного
интервала, соответствующего объему выборки n2 = 36.
, т.е. доверительный интервал, соответствующий объему выборки
n1 = 84, будет меньше доверительного
интервала, соответствующего объему выборки n2 = 36.
б) 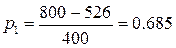
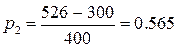
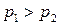
Исходя из формулы (7.1)
следует, что при возрастании надежности P значение D увеличивается, т.к. увеличивается значение функции
Стьюдента  . Следовательно,
. Следовательно, 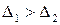 , т.е. доверительный интервал, соответствующий надежности
, т.е. доверительный интервал, соответствующий надежности  будет больше доверительного интервала, соответствующего
надежности
будет больше доверительного интервала, соответствующего
надежности 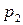 .
.
в) 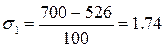
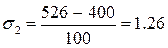

Исходя
из формулы (7.1) следует, что при возрастании среднего квадратического
отклонения значение D увеличивается. Следовательно 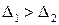 , т.е. доверительный
интервал, соответствующий средне
квадратическому отклонению
, т.е. доверительный
интервал, соответствующий средне
квадратическому отклонению 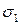 , будет больше доверительного интервала, соответствующего
средне квадратическому отклонению
, будет больше доверительного интервала, соответствующего
средне квадратическому отклонению 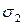
Задание 8
1)
Дайте понятие функциональной и корреляционной зависимости.
Ответ:
Функциональная
зависимость – это зависимость, при которой каждому значению одной переменной,
строго соответствует одно определенное значение другой переменной.
Зависимость,
при которой одному значению переменной может соответствовать (в силу наслоения
действия других причин) множество значений другой переменной, называют
корреляционной.
2)
Коэффициент корреляции. Его смысл и свойства.
Ответ:
Направление
и теснота связи между признаками x и y оцениваются
на основе коэффициента корреляции, который рассчитывается по формуле: 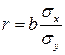 . Коэффициент корреляции принимает значения в интервале -1 до
+1.
. Коэффициент корреляции принимает значения в интервале -1 до
+1.
Принято считать, что |r|<0.30, то связь слабая, при 0.30<|r|<0.70 – средняя, при |r|>0,70 – сильная, или тесная.
Когда |r|=1 – связь функциональная. Если же r»0, то это дает основание говорить об
отсутствии линейной связи между x и y.
3)
Оцените тесноту связи и направления связи между признаками x и
y, если известно:
b– коэффициент регрессии,

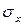 и
и 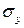 - среднеквадратического отклонения
признаков x и y.
- среднеквадратического отклонения
признаков x и y.
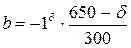
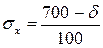
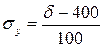
Решение:
В
нашем случае 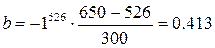
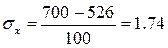
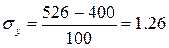
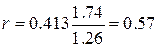
Коэффициент корреляции показывает, что связь между признаками
x и y средняя и прямая, т.е. при
возрастании факторного признака x значение результативного признака y увеличивается.