Задача
№1.
Совхоз для
кормления животных использует два вида корма. В дневном рационе животного
должно содержаться не менее 6 единиц питательного вещества А и не менее 12 единиц питательного вещества В. Какое количество корма надо расходовать ежедневно на одно
животное, чтобы затраты были минимальными? Использовать данные таблицы.
|
Питательное
вещество
|
Количество питательных веществ в 1 кг корма
|
|
1
|
2
|
|
А
|
2
|
1
|
|
В
|
2
|
4
|
|
Цена 1 кг корма, тыс. руб.
|
0,2
|
0,3
|
Построить экономико-математическую модель
задачи, дать необходимые комментарии к ее элементам и получить решение
графическим методом. Что произойдет, если решать задачу на максимум, и почему?
Решение.
ЭММ задачи.
Пусть: х1 (кг) –
количество корма типа 1, которое следует включить в дневной рацион животного.
х2
(кг) - количество корма типа 2, которое следует включить в дневной рацион
животного.
Таким образом
дневной рацион животного формально представляет собой вектор Х = (х1; х2).
Математическая
задача по критерию минимальных затрат на дневной рацион животного записывается
следующим образом:
min f(x) = 0.2x1 +
0.3x2
2x1 + x2 ≥ 6 → ограничение по
содержание питательного вещества А
2x1 + 4x2 ≥ 12 → ограничение по содержанию питательного вещества В
x1,2 ≥ 0
Построим ОДР
этой задачи.
Прямые
ограничений означают, что ОДР задачи будет лежать в I четверти прямоугольной системе
координат. Функциональные ограничения неравенства определяющие область,
являются пересечением полуплоскостей с граничными прямыми.
I.
2x1 + x2 = 6
 II.
2x1 + 4x2 = 12
II.
2x1 + 4x2 = 12
Пересечение
указанных полуплоскостей в I
четверти представляет собой неограниченную многоугольную область с вершинами АВС (ОДР).
Для
определения направления движения к оптимуму, построим вектор-градиент, соединив
его вершину (0,2;0,3) с началом
координат О (0;0).
Построим
некоторую линию уровня перпендикулярно вектору градиенту. Этой линией уровня
отвечает прямая ОХ.
При
минимизации ЦФ необходимо перемещать линию уровня противоположно направлению
вектора-градиента. Придельными точками при таком движении линии уровня ОХ является, соответственно, точка В, далее она выходит из ОДР.
Координаты
точки В определим, решив систему
уравнений:
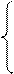
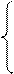
2x1 + x2 = 6 x1 = 2
→
2x1 + 4x2 =
12 x2 = 2
Решением этой
системы уравнений являются сведущие значения переменных:
x1 = 2, x2 = 2.
Минимальное
значение ЦФ равно:
min f(x) = 0.2*2 + 0.3*2 = 1
ВЫВОД:
Таким образом
в рассматриваемой задаче Савхозу следует рекомендовать включать в дневной
рацион одного животного ежедневно 2
кг корма типа 1 и 2 кг корма типа 2. В этом случае ожидаются
минимальные затраты в сумме 1 тыс. руб.
При решении
на максимум задача не будет иметь решений поскольку не существует конечного
максимума на неограниченном множестве допустимых решений.
Задача
№2.
Для
изготовления четырех видов продукции используют три вида сырья. Запасы сырья,
нормы его расхода и цены реализации единицы каждого вида продукции приведены в
таблице.
|
Тип сырья
|
Нормы расхода сырья на одно изделие
|
Запасы сырья
|
|
А
|
Б
|
В
|
Г
|
|
I
|
1
|
0
|
2
|
1
|
180
|
|
II
|
0
|
1
|
3
|
2
|
210
|
|
III
|
4
|
2
|
0
|
4
|
800
|
|
Цена
изделия
|
9
|
6
|
4
|
7
|
|
Требуется:
1.
Сформулировать прямую оптимизационную
задачу на максимум выручки от реализации готовой продукции, получить
оптимальный план выпуска продукции.
2.
Сформулировать двойственную задачу и
найти ее оптимальный план с помощью теорем двойственности.
3.
Пояснить нулевые значения переменных в
оптимальном плане.
4.
На основе свойств двойственных оценок и
теорем двойственности:
– проанализировать
использование ресурсов в оптимальном плане исходной задачи;
– определить,
как изменятся выручка и план выпуска продукции при увеличении запасов сырья II и III видов на 120 и 160 единиц
соответственно и уменьшении на 60 единиц запасов сырья I вида;
– оценить
целесообразность включения в план изделия Д
ценой 12 единиц, на изготовление которого расходуется по две единицы каждого
вида сырья.
Решение.
1. Сформулировать
прямую оптимизационную задачу на максимум выручки от реализации готовой
продукции, получить оптимальный план выпуска продукции.
Пусть x1, x2, x3 и х4
– объемы производства продукции каждого вида.
Целевая функция имеет вид: max f(x) = 9x1 +
6x2 +
4x3 +
7x4,
а ограничения
по ресурсам: x1 + 2x3 +
x4 ≤
180
x2 + 3x3 + 2x4
≤ 210
4x1 + 2x2 + 4x4 ≤ 800
x1, 2, 3, 4 ≤ 0
Поиск оптимально плана выпуска продукции.
Решим задачу
при помощи настройки Excel.
Введем
исходные данные.
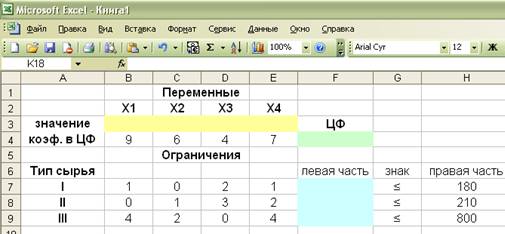
Опишем ЦФ с помощью функции –
«СУММПРОИЗВ».
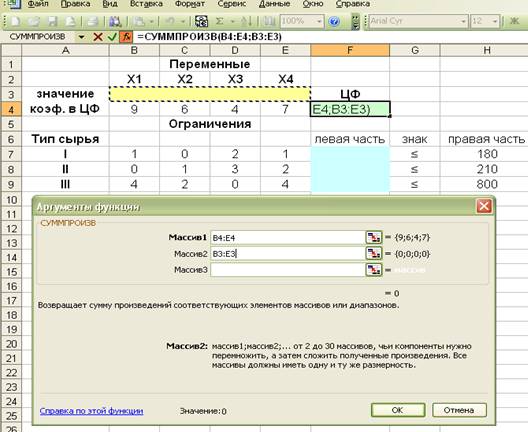
Введем данные
для левых частей ограничений. В «Поиске
решений» введем направления ЦФ, адреса искомых переменных, добавим
ограничения.
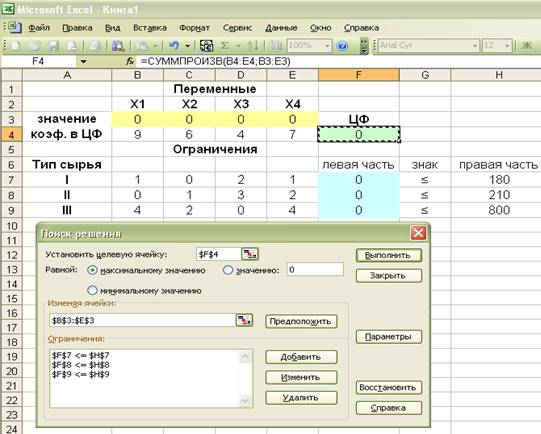
Введем
параметры для решения ЗЛП.
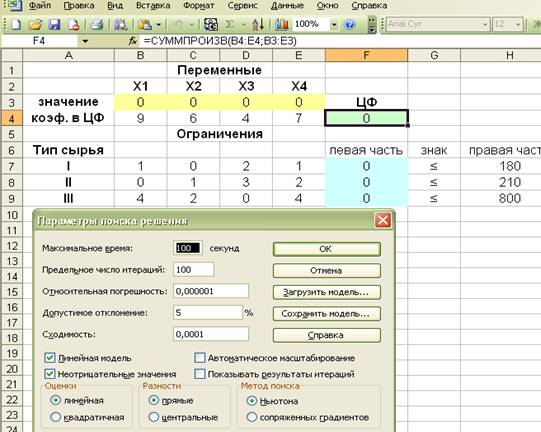
После ввода
параметров следует нажать кнопку «Выполнить».
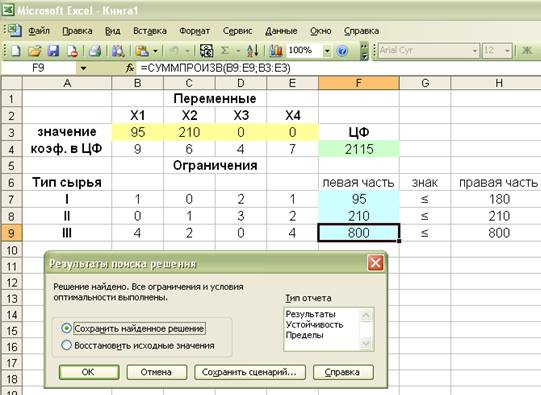
Полученное решение означает, что максимальные доход 2115 ед. предприятие может получить при
выпуске 95 ед. первой продукции, 210 ед. второй продукции, 0 ед. третьей продукции и 0 ед. четвертой продукции. Третий и
четвертый вид продукции не выгодно выпускать, т.к. затраты превышают цену.
Отчет по устойчивости.
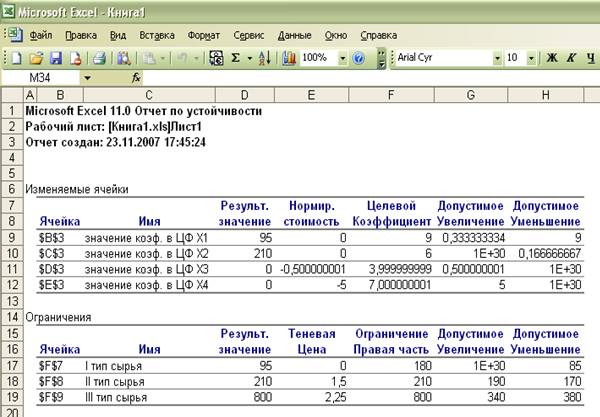
В отчете по устойчивости мы видим, что нормированная стоимость для
производства продукций В и Г видов равна, соответственно, -0,5 и -5 – это означает, что если несмотря на оптимальный план (95, 210, 0, 0), попробуем включить в
план выпуска продукцию В и Г вида, то новый план выпуска принесет
нам доход 2109,5 ед., что на 5,5 ед. меньше, чем прежнее оптимальное
решение.
Предельные значения приращения целевых коэффициентов, при которых
сохраняется первоначальное оптимальное решение. Допустимое увеличение цены
продукции В и Г видов равно, соответственно, 0,5
ед. и 5 ед., а допустимое уменьшение практически неограниченно
1E+30. Это означает, что если
цена продукции В и Г видов возрастет более чем на 0,5 ед. и 5 ед., то оптимальное решение изменится: станет целесообразным
производить продукцию видов В и Г. А если их цена будет снижаться
вплоть до нуля, то оптимальное решение (95,
210, 0, 0) останется прежним.
В рассматриваемой задаче являются дефицитные типы сырья (II и III типы).
Чтобы обеспечить увеличение производства продукции необходимо увеличить II тип сырья, самое большое,
на 190, а III тип сырья
– на 340.
Отчет по результатам.
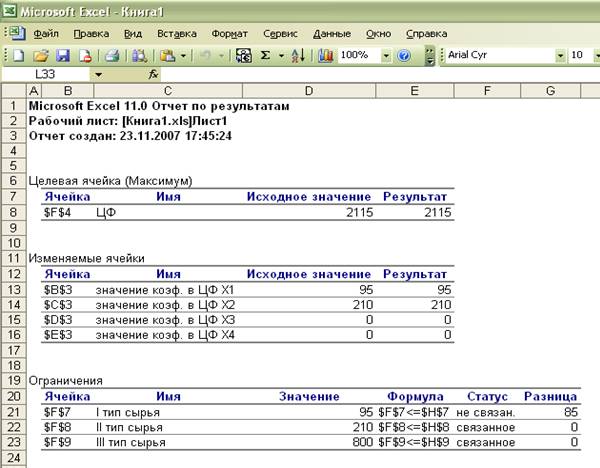
В отчете по
результатам содержатся оптимальные значения переменных х1, х2, х3
и х4,
которые соответственно равны 95; 210; 0; 0, значение целевой
функции – 2115, а так же левые части ограничений.
2. Сформулировать двойственную задачу и найти ее оптимальный план с
помощью теорем двойственности.
Пусть y1, y2, y3 – двойственные оценки типов
ресурсов соответственно.
Целевая
функция имеет вид: min g(y) = 180y1 +
210y2 +
800y3
Функциональные
ограничения: y1 +0y2 +
4y3
≥ 9
0y1 + y2 + 2y3 ≥
6
2y1 +
3y2 +
0y3
≥ 4
y1 + 2y2 +
4y3
≥ 7
y1, 2, 3
≥ 0
Найдем
оптимальный план этой задачи, используя основную теорему двойственности:
max f(x) = 95
∙ 9 + 210 ∙ 6 + 0 ∙ 4 + 0 ∙ 7 = 2115
Проверим,
является ли указанный в условии задачи план допустимым решением:
По типу сырья
I: 1 ∙ 95 + 0 ∙ 210 + 2
∙ 0 + 1 ∙ 0 ≤ 180
По типу сырья
II: 0 ∙ 95 + 1 ∙ 210 + 3
∙ 0 + 2 ∙ 0 = 210
По типу сырья
III: 4 ∙ 95 + 2 ∙ 210 + 0
∙ 0 + 4 ∙ 0 = 800
Так же
получим: y1 (95 – 180) = 0,
т.к. 95 < 180, то y1 = 0
y2 (210 – 210) = 0
y3 (800 - 800) = 0
Следовательно,
план оптимальный. Ресурс I
остается в избытке, а ресурсы II и III
расходуются полностью.
Воспользуемся
соотношением второй теоремой двойственности:

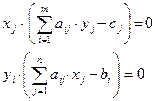
т.к. х1
= 95 > 0 и х2 = 210 > 0, то первое и второе
ограничения двойственной задачи обращаются в равенства:
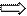
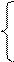 y1 + 4y3
= 9
y1 + 4y3
= 9 y1 = 0
y1 = 0
y2 + 2y3
= 6 y2 = 1,5
y1 = 0 y3 = 2,25
y3 = 2,25
Вычислим
значения целевой функции двойственной задачи:
g(y) = 180
∙ 0 + 210 ∙ 1,5 + 800 ∙ 2,25 = 2115
Таким
образом, приведенный в условии план является оптимальным.
3. Пояснить нулевые значения переменных в оптимальном плане.
Если
изготовление продукции определенного вида вошло в план (хj > 0), то в
двойственных оценках оно не убыточное, т.е. стоимость ресурсов, затраченных на
производство единицы продукции, равна его цене. Такая продукция эффективна,
выгодна с точки зрения принятого критерия оптимальности. В этой задаче – это
продукция видов В и Г.
Если
стоимость ресурсов, затраченных на производство одного вида продукции, больше
его цены, то этот вид продукции не войдет в оптимальный план из-за его
убыточности.
В данной
задаче в план производства не вошли продукция видов В и Г, потому что
затраты по ним превышают цену на 0,5 ед.
и 5 ед. соответственно. Это можно
подтвердить, подставив в ограничения двойственной задачи оптимальные значения
вектора Y:
y1 +0y2 + 4y3
≥ 9
0y1 +
y2 +
2y3 ≥
6
2y1 +
3y2 +
0y3
≥ 4
y1 + 2y2 +
4y3
≥ 7
y1, 2, 3
≥ 0
1
∙ 0 + 0 ∙ 1,5 + 4 ∙ 2,25 = 9
0
∙ 0 + 1 ∙ 1,5 + 2 ∙ 2,25 = 6
2
∙ 0 + 3 ∙ 1,5 + 0 ∙ 2,25 = 4,5 > 4
1
∙ 0 + 2 ∙ 1,5 + 4 ∙ 2,25 = 12 > 7
Разницу между
правыми и левыми частями ограничений двойственной задачи видно в «Отчете по устойчивости» в столбце «Нормируемая стоимость».
4.1
Проанализировать использование
ресурсов в оптимальном плане исходной задачи.
Тип сырья I является недефицитным (y1 = 0).
Ресурсы II и III
являются дефицитными, причем ресурс III более дефицитный, чем ресурс II (y3 = 2,25; y2 = 1,5; y3 > y2).
Найдем норму
заменяемости для дефицитных ресурсов:
y3 : y2 = 2,25 : 1,5 =
1,5
Следовательно,
ресурс III в 1,5
раза более эффективен, чем ресурс II с точки зрения влияния на максимум продукции.
4.2 Определить, как изменятся выручка
и план выпуска продукции при увеличении запасов сырья II и III видов на 120 и 160 единиц соответственно и уменьшении на 60
единиц запасов сырья I вида.
Будем
считать, что данные изменения объемов ресурсов находятся в пределах
устойчивости оптимального решения (в пределах устойчивости двойственных
оценок), тогда по третьей теореме двойственности (теореме об оценках) имеем:
Δf(x) = Δbi yi
Δf(x) = (+120) ∙ 1,5 + (+160) ∙ 2,25 + (-60) ∙ 0 = 540
Решая эту ЗЛП симплекс-методом при помощи настройки Excel, получим
следующее:
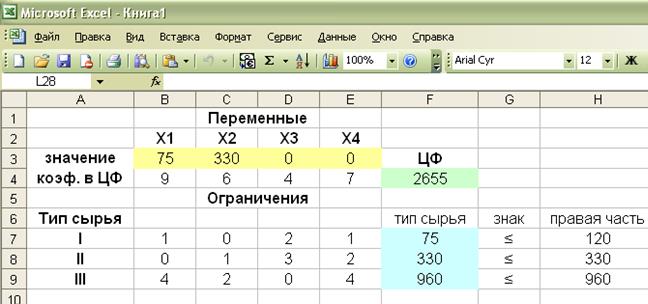
Полученное решение означает, что максимальные доход, увеличившийся с 2115
ед. до 2655 ед. предприятие
может получить при выпуске 75 ед.
первой продукции, 330 ед. второй
продукции, 0 ед. третьей продукции и
0 ед. четвертой продукции. Третий и
четвертый вид продукции не выгодно выпускать, т.к. затраты превышают цену.
Отчет по результатам.
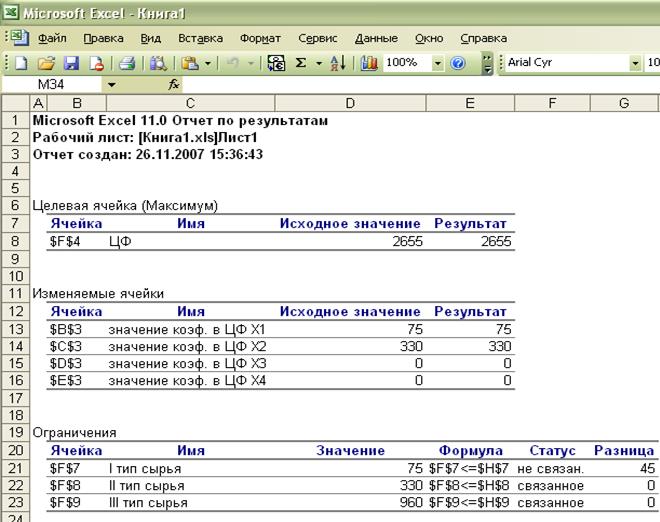
В отчете по
результатам содержатся оптимальные значения переменных х1, х2, х3
и х4,
которые соответственно равны 75; 330; 0; 0, значение целевой
функции – 2655, а так же левые части ограничений.
Отчет по устойчивости.
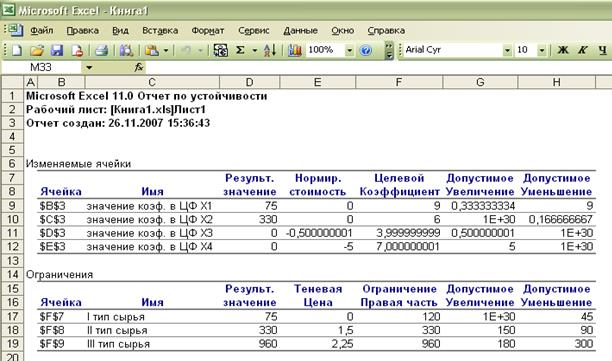
В отчете по устойчивости мы видим, что нормированная стоимость для
производства продукций В и Г видов равна, соответственно, -0,5 и -5 – это означает, что если несмотря на оптимальный план (75, 330, 0, 0), попробуем включить в
план выпуска продукцию В и Г вида, то новый план выпуска принесет
нам доход 2649,5 ед., что на 5,5 ед. меньше, чем прежнее оптимальное
решение.
Предельные значения приращения целевых коэффициентов, при которых
сохраняется первоначальное оптимальное решение. Допустимое увеличение цены
продукции В и Г видов равно, соответственно, 0,5
ед. и 5 ед., а допустимое уменьшение практически
неограниченно 1E+30. Это означает,
что если цена продукции В и Г видов возрастет более чем на 0,5 ед. и 5 ед., то оптимальное решение изменится: станет целесообразным
производить продукцию видов В и Г. А если их цена будет снижаться
вплоть до нуля, то оптимальное решение (75,
330, 0, 0) останется прежним.
В рассматриваемой задаче являются дефицитные типы сырья (II и III типы).
Чтобы обеспечить увеличение производства продукции необходимо увеличить II тип сырья, самое большое,
на 90, а III тип сырья
– на 300.
Решим эту же
задачу «вручную». Запишем исходную и двойственную ЗЛП с измененными объемами
ресурсов.
|
Исходная:
max f(x) = 9x1
+ 6x2 + 4x3 + 7x4
x1 +
0x2 + 2x3 + x4 ≤ 120
0x1 +
x2 + 3x3 + 2x4 ≤ 330
4x1 +
2x2 + 0x3 + 4x4 ≤ 960
x1, 2, 3, 4 ≥
0
|
Двойственная:
min g(y) = 120y1
+ 330y2 + 960y3
y1 + 0y2
+ 4y3
≥ 9
0y1
+ y2
+ 2y3
≥ 6
2y1
+ 3y2
+ 0y3
≥ 4
y1 + 2y2
+ 4y3
≥ 7
y 1, 2, 3 ≥ 0
|
Воспользуемся
соотношением второй теоремой двойственности (теорема о дополняющей нежестокости):
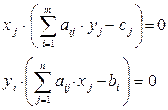
Рассмотрим
первые соотношения (их два):
y1 +
0y2 +
4y3 =
9
0
+ 4 ∙ 2,25 = 9
Следовательно, про x1 ничего
сказать нельзя.
0y1 +
y2 +
2y3 =
6
1,5
+ 2,25 ∙ 2 = 6
Следовательно, про x2 тоже
ничего сказать нельзя.
2y1 +
3y2 +
0y3 =
4
2
∙ 0 + 3 ∙ 1,5 ≠ 4, →
х3 = 0 (затраты больше цены)
y1 +
2y2 +
4y3 =
7
0
∙ 2 + 1,5 + 4 ∙ 2,25 ≠ 7, → х4 = 0
(затраты больше цены)
Рассмотрим
вторые соотношения:
y1 = 0,
ничего сказать нельзя
y2 = 1,5 -
второе ограничение обращается в равенство
х2
+ 3х3 + 2х4 = 330
y3 = 2,25 –
третье ограничение обращается в равенство
4х1
+ 2х2 + 4х4 = 960
Запишем
систему уравнений и решим ее:
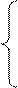
х2
+ 3х3 + 2х4 = 330 х1 = 75
 4х1
+ 2х2 + 4х4 = 960 х2 = 330
4х1
+ 2х2 + 4х4 = 960 х2 = 330
х3
= 0  х3 = 0
х3 = 0
х4
= 0 х4 = 0
х4 = 0
f(x) = 9 ∙ 75 + 6 ∙
330 + 4 ∙ 0 + 7 ∙ 0 = 2655
Это совпадает
с выводом, сделанным ранее на основании «теоремы об оценках».
4.3 Оценить целесообразность включения в план
изделия Д ценой 12 единиц, на изготовление которого расходуется по две единицы
каждого вида сырья.
Это задание выполняется на основе третьего свойства двойственных
оценок, т.е. оценки как определение эффективности.
Δf(x) = Δbi yi
Δ4 = 2 ∙ 0 + 2 ∙ 1,5 + 2 ∙ 2,25 – 12
= -4,5 < 0
Следовательно,
данную продукцию выпускать целесообразно (затраты меньше цены).
Задача
№3
Промышленная
группа предприятий (холдинг) выпускает продукцию трех видов, при этом каждое из
трех предприятий группы специализируется на выпуске продукции одного вида:
первое предприятие специализируется на выпуске продукции одного вида, второе
предприятие – продукции второго вида; третье предприятие – продукции третьего
вида. Часть выпускаемой продукции потребляется предприятиями холдинга (идет
внутреннее потребление), остальная часть поставляется за его пределы (внешним
потребителям, является конечным продуктом). Специалистам управляющей компании
получены экономические оценки aij (i = 1, 2, 3; j = 1, 2, 3) элементов
технологической матрицы А (норм
расхода, коэффициентов прямых материальных затрат) и элементов yi вектора конечной продукции Y.
Требуется:
1.
Проверить продуктивность технологической
матрицы А = (aij)
(матрицы коэффициентов прямых материальных затрат).
2.
Построить баланс (заполнить таблицу)
производства и распределения продукции предприятий холдинга.
Решение.
Технологическая матрица А.
|
Отрасли
|
Коэффициенты прямых поставок,
aij
|
Конечный продукт,
Yi
|
|
1
|
2
|
3
|
|
1
|
0,0
|
0,1
|
0,2
|
180
|
|
2
|
0,1
|
0,2
|
0,1
|
200
|
|
3
|
0,2
|
0,1
|
0,2
|
200
|
1.
Проверить
продуктивность технологической матрицы А
= (aij)
(матрицы коэффициентов прямых материальных затрат).
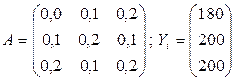
Неотрицательная
матрица А будет называться продуктивной, если существует такой
неотрицательный вектор Х ≥ 0, что Х
>АХ. Очевидно, что это условие означает существование положительного
вектора конечной продукции Y > 0 для межотраслевого баланса.
Найдем B = (E - A)-1, где В
– матрица коэффициентов полных материальных затрат.
|E – A| = 1 ∙ 0,8
∙ 0,8 + (-0,1) ∙ (-0,1) ∙ (-0,2) + (-0,1) ∙ (-0,1)
∙ (-0,2) - (-0,2) ∙ 0,8 ∙ (-0,2) - (-0,1) ∙ (-0,1)
∙ 1 - (-0,1) ∙ (-0,1) ∙ 0,8 = 0,586
Т.к |E – A| ≠ 0, то
существует обратная к ней матрица.
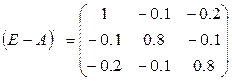
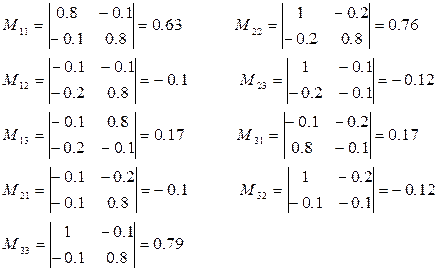
а11 = (-1)2 ∙ 0,63 = 0,63 а23 = (-1)5
∙ (-0,12) = 0,12
а12 = (-1)3 ∙ (-0,1) = 0,1 а31 = (-1)4
∙ 0,17 = 0,17
а13 = (-1)4 ∙ 0,17 = 0,17 а32 = (-1)5
∙ (-0,12) = 0,12
а21 = (-1)3 ∙ (-0,1) = 0,1 а33 = (-1)6
∙ 0,79 = 0,79
а22 = (-1)4 ∙ 0,76 = 0,76
т.о. 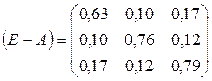
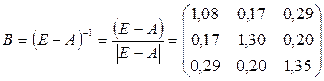
Все элементы
матрицы коэффициентов полных затрат В неотрицательны, следовательно,
матрица А – продуктивна.
2.
Построить
баланс (заполнить таблицу) производства и распределения продукции предприятий
холдинга.
Определим
межотраслевые поставки и найдем величины валовой продукции каждого предприятия.
xij = aij
∙ Xj
X = B ∙ Yi
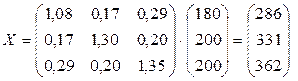 - величина
валовой продукции каждого предприятия.
- величина
валовой продукции каждого предприятия.
Находим
матрицу межотраслевых поставов продукции:
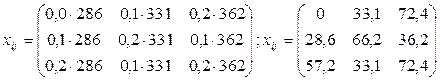
Итог
материальных затрат любой потребляющей отрасли и ее условно чистой продукции
равен валовой продукции этой отрасли. Данный вывод можно записать в виде
соотношения:
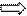
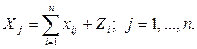

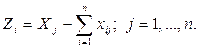
Z1 =
286 – (0 + 28,6 + 57,2) = 200
Z2 =
331 – (33,1 + 66,2 + 33,1) = 199
Z3 =
362 – (72,4 + 36,2 + 72,4) = 181
Валовая
продукция той или иной отрасли равна сумме материальных затрат, потребляющих ее
продукцию отраслей и конечной продукции данной отрасли:
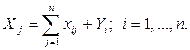
Х1 = (0 + 33,1 + 72,4) + 180 = 286
Х2 = (28,6 + 66,2 + 36,2) +200 = 331
Х3 = (57,2 + 33,1 + 72,4) + 200 = 362
Заполняем
схему МОБ (модели межотраслевого
баланса).
|
Предприятия (виды продукции)
|
Коэффициенты прямых затрат, aij
|
Конечный продукт, Yi
|
Валовый продукт, Хi
|
|
1
|
2
|
3
|
|
1
|
0
|
33,1
|
72,4
|
180
|
286
|
|
2
|
28,6
|
66,2
|
36,2
|
200
|
331
|
|
3
|
57,2
|
33,1
|
72,4
|
200
|
362
|
|
Условно чистая продукция, Zj
|
200
|
199
|
181
|
580
|
|
|
Валовый продукт, Хj
|
286
|
331
|
362
|
|
979
|
Необходимо,
чтобы выполнялись следующие условия:
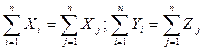 - что мы и
видим из выше представленной таблицы.
- что мы и
видим из выше представленной таблицы.
Задача
№4
В течение
десяти последовательных недель фиксировался спрос Y(t) (млн.руб.) на кредитные
ресурсы финансовой компании. Временной ряд Y(t) этого показателя приведен ниже в таблице.
|
Номер варианта
|
Номер наблюдения (t = 1, 2, …, 9)
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
2
|
43
|
47
|
50
|
48
|
54
|
57
|
61
|
59
|
65
|
Требуется:
1.
Проверить наличие аномальных наблюдений.
2.
Построить линейную модель Ŷ(t) = a0 + a1t, параметры которой
оценить МНК (Ŷ(t) – расчетные, смоделированные значения временного
ряда).
3.
Оценить адекватность построенных моделей,
используя свойства независимости остаточной компоненты, случайности и
соответствия нормальному закону распределения (при использовании R/S-критерия взять
табулированные границы 2,7-3,7).
4.
Оценить остаточность моделей на основе
использования средней относительной ошибки аппроксимации.
5.
По двум построенным моделям осуществить
прогноз спроса на следующие две недели (доверительный интервал прогноза
рассчитать при доверительной вероятности p = 70%).
6.
Фактические значения показателя,
результаты моделирования и прогнозирования представить графически.
Вычисления
провести с одним знаком в дробной части. Основные промежуточный результаты
вычислений представить в таблицах (при использовании компьютера представить
соответствующие листинги с комментариями).
Решение:
Для
диагностики аномальных наблюдений разработаны различные критерии, например
метод Ирвина. Вычислим для всех наблюдений величину λt.
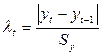 , где
, где 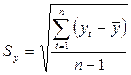 ,
, 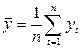
|
t
|
y(t)
|
(yt
- ý)2
|
λt
|
|
1
|
43
|
116,16049
|
-
|
|
2
|
47
|
45,938272
|
0,548437
|
|
3
|
50
|
14,271605
|
0,411328
|
|
4
|
48
|
33,382716
|
0,27422
|
|
5
|
54
|
0,0493827
|
0,822656
|
|
6
|
57
|
10,382716
|
0,411328
|
|
7
|
61
|
52,160494
|
0,548437
|
|
8
|
59
|
27,271605
|
0,27422
|
|
9
|
65
|
125,93827
|
0,822656
|
|
5
|
484
|
425,55556
|
|
|
ср знач
|
сумма
|
сумма
|
|
yср = 53,778; Sy = 7,293
Из
представленной выше таблицы мы видим, что λt не превышает табличный
уровень (для 10 наблюдений, значение критерия Ирвина равно 1,5), следовательно,
уровни yt не считаются аномальными.
Построим
линейную однопараметрическую модель регрессии Y от t (Ŷ(t) = a0 + a1t) при помощи надстройки Excel.
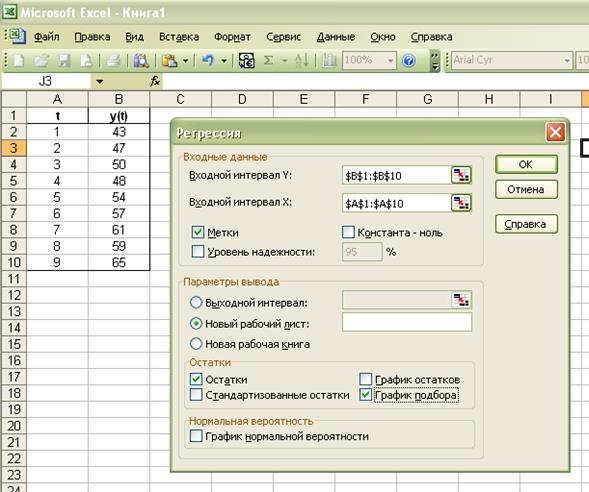
И получили следующие данные, из которых видно
уравнение регрессии зависимости yt (спрос на кредитные ресурсы компании) от t (время),
которое имеет вид: y(t) = 40.86 + 2.58t
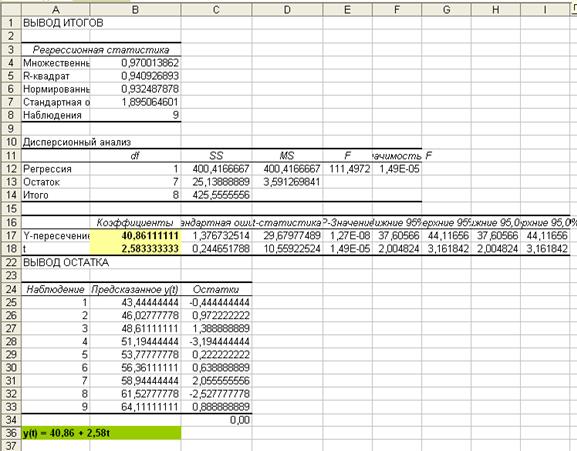
При
вычислении «вручную» по формулам получаем те же результаты.
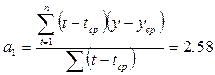
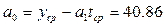
Это видно из
таблицы.
|
t
|
y(t)
|
t - tср
|
(t - tср)2
|
y - yср
|
(t - tср)(y
- yср)
|
|
1
|
43
|
-4
|
16
|
-10,77777778
|
43,11111111
|
|
2
|
47
|
-3
|
9
|
-6,777777778
|
20,33333333
|
|
3
|
50
|
-2
|
4
|
-3,777777778
|
7,555555556
|
|
4
|
48
|
-1
|
1
|
-5,777777778
|
5,777777778
|
|
5
|
54
|
0
|
0
|
0,222222222
|
0
|
|
6
|
57
|
1
|
1
|
3,222222222
|
3,222222222
|
|
7
|
61
|
2
|
4
|
7,222222222
|
14,44444444
|
|
8
|
59
|
3
|
9
|
5,222222222
|
15,66666667
|
|
9
|
65
|
4
|
16
|
11,22222222
|
44,88888889
|
|
5
|
484
|
|
60
|
0,00
|
155
|
|
ср знач
|
сумма
|
|
сумма
|
ср знач
|
сумма
|