Задача 1
На территории города
имеется три телефонные станции А, Б, и В. Незадействованные ёмкости станций
составляют на станции А-QА, Б-QБ, В-QВ номеров (таблица 1.1). Потребности новых районов застройки
города в телефонах составляют: 1-Q1, 2-Q2, 3-Q3, 4-Q4 номеров таблицы (таблицы 1.2).
Необходимо составить
экономико-математическую модель задачи с помощью модифицированного метода
линейного программирования найти вариант распределения ёмкостей телефонных
станций между районами новой застройки, который обеспечивал бы минимальные
затраты как на строительство, так и на эксплуатацию линейных сооружений
телефонной сети. Естественно, что таким вариантом при прочих равных условиях
будет такое распределение ёмкости, при котором общая протяженность абонентских
линий будет минимальной.
Таблица 1.1
Незадействованные ёмкости телефонных станций.
Таблица 1.2 Спрос на
установку телефонов
|
Q1
|
Q2
|
Q3
|
Q4
|
|
1200
|
3700
|
4100
|
3000
|
Таблица 1.3 Среднее
расстояние от станции до районов застройки, км.
|
Станции
|
Районы
|
|
1
|
2
|
3
|
4
|
|
А
|
4
|
5
|
6
|
4
|
|
Б
|
3
|
2
|
1
|
4
|
|
В
|
6
|
7
|
5
|
2
|
Решение:
Суммарный спрос
потребителей станции больше, чем суммарная мощность станции
(1200+3700+4100+3000=1200>3000+4000+2000=9000). Введем “фиктивную станцию” и
в таблицу станций добавим дополнительную строку. Для этого мощность “фиктивной
станции - Г” следует принять равной 12000-9000=3000.
Исходные данные для
решения задачи приведены в таблице 1.1.
|
Станции
|
Средние расстояния от станций до
районов застройки
|
|
|
1
|
2
|
3
|
4
|
|
|
А
|
4
|
5
|
6
|
4
|
3000
|
|
Б
|
3
|
2
|
1
|
4
|
4000
|
|
В
|
6
|
7
|
5
|
2
|
2000
|
|
Г
|
0
|
0
|
0
|
0
|
3000
|
|
|
1200
|
1800
|
4100
|
3000
|
|
|
|
|
|
|
|
|
Первоначальное
распределение телефонных номеров найдем по методу наименьших затрат.
|
1200
|
3700
|
4100
|
3000
|
|
3000
|
4
|
5 1900
|
6 100
|
4 1000
|
|
4000
|
3
|
2
|
1 4000
|
4
|
|
2000
|
6
|
7
|
5
|
2 2000
|
|
3000
|
0 1200
|
0 1800
|
0
|
0
|
Определим протяженность
линии, для чего требуемую емкость умножим на среднее расстояние от станции до
района застройки:
1900*5+1000*4+4000+2000*2+0+0+0=22100
км.
Установим оптимально ли
это распределение, для этого исследуем все занятые клетки:
a1+b2=5, a1+b3=6, a1+b4=4,
a2+b3=1, a3+b4=2, a4+b1=0,
a4+b2=0
Положим a1=0, тогда a1= a4=-5, a3=-2,
b1= b2=5, b3=6, b4=4.
Теперь исследуем
свободные клетки:
a1+b1=5, a2+b1=0, a2+b2=0,
a2+b4=-1, a3+b1=3, a3+b2=3,
a3+b3=4, a4+b3=1, a4+b4=-1.
Условие оптимальности не
выполняется для клеток:
(1,1), (2,4), (4,3) и
(4,4)
Это показывает
возможность дальнейшего улучшения распределения емкости между районами застройки.
Улучшенный вариант решения приведен в таблице 1.2
Таблица 1.2
|
1200
|
3700
|
4100
|
3000
|
|
3000
|
4 100
|
5 1900
|
6
|
4 1000
|
|
4000
|
3
|
2
|
1 4000
|
4
|
|
2000
|
6
|
7
|
5
|
2 2000
|
|
3000
|
0 1100
|
0 1800
|
0 100
|
0
|
Определим протяженность
линии, для чего требуемую емкость умножим на среднее расстояние от станции до
района застройки:
100*4+1900*5+1000*4+4000+2000*2+0+0+0=21900
км.
Аналогично проверяя на
оптимальность это решение приходим в выводу, что распределение телефонов между
районами оптимально.
Задача 2
Необходимо оценить работу
автоматической телефонной станции (АТС), которая имеет n линий связи. Моменты поступления
вызовов на станцию являются случайными и независимы друг от друга. Средняя
плотность потока равна l вызовов в единицу времени.
Продолжительность каждого разговора является
величиной случайной и подчинена показательному закону распределения.
Среднее время одного разговора равно tобс единиц времени.
Таблица 2.1 Исходные
данные
|
Кол-во линий, n
|
Плотность потока, l
|
Среднее время разговора tобс
|
|
7
|
3
|
2
|
Решение:
АТС представляет
7-канальную систему массового обслуживания. При расчете на часовой интервал
получаем tобс= 2, l=3, b=1,8. Число вызовов не будет
постоянно возрастать, т.к. выполняется условие b<n. Определим P0:
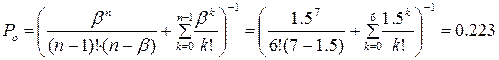

P0=0,223 означает, что 22,3% времени
работы АТС не будет занято. Вероятность того, что поступивший вызов столкнется
с тем, что линия связи будет занята обслуживанием и он будет некоторое время
ожидать обслуживания:
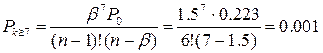
Т.е. в одном случае из
ста вызов столкнется с рассматриваемой ситуацией. Средний размер очереди:
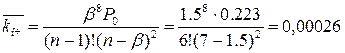 , т.е. в среднем
очереди не будет.
, т.е. в среднем
очереди не будет.
Таким образом можно
отметить, что в системе практически полностью используется рабочее время АТС и
очередей не будет.
Задача 3
Предприятие выпускает
товары народного потребления, изготовляя их отдельными партиями. Чем больше
размер этих партий, тем это более выгодно предприятию. Поэтому, предприятие заинтересовано в отдельные месяцы
выпускать больше изделий, чем это нужно для удовлетворения спроса, а излишки
хранить на складе для их реализации в последующие месяцы. Хранение изделий на
складе сопряжено с дополнительными затратами.
Необходимо определить план
выпуска изделий, при котором общая сумма на их производство и хранение была
минимальной, а спрос на необходимые изделия был бы удовлетворен своевременно и
полностью
Для этого потребуется:
1) Построить динамическую
экономико-математическую модель помесячного удовлетворения спроса на изделия
при минимуме суммарных затрат на их производство и хранение.
2) Используя метод
динамического программирования, найти оптимальную стратегию предприятия по
производству изделий.
Таблица 3.1 Исходные
данные
|
Запас изделий на складе к началу
планируемого
периода, тыс. ед.
|
Ёмкость склада, тыс. ед.
|
Максимальная возможность по
производству изделий, тыс. ед.
|
|
2
|
3
|
4
|
|
Спрос на изделия, тыс. ед.
|
|
в январе
|
в феврале
|
в марте
|
в апреле
|
|
3
|
3
|
2
|
2
|
Таблица 3.2 Затраты на производство
|
Партия изделий, тыс.ед.
|
1
|
2
|
3
|
4
|
|
Затраты на производство всей партии, ден. ед.
|
15
|
19
|
22
|
24
|
Затраты на хранение каждой тысячи изделий составляет 2
ден. ед.
Решение:
Примем следующие
обозначения:
|
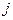
|
Номер месяца (j=1,..,4)
|
|

|
Число изделий, производимых в j-ом месяце
|
|
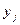
|
Величина запаса к началу j-го месяца
|
|
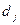
|
Спрос на изделия в j-ом
месяце
|
|
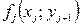
|
Затраты на хранение и производство изделий в j-ом месяце
|
Тогда, задача
состоит в том, чтобы найти план производства 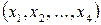 компоненты которого удовлетворяют условиям
материального баланса:
компоненты которого удовлетворяют условиям
материального баланса:
 , где
, где 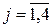
и минимизируют суммарные
затраты за весь планируемый период:
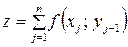
причем по смыслу задачи 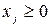 ,
, 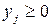 , при
, при 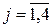
Т.к. объем произведенной
продукции  на этапе j может быть
настолько велик, что запас
на этапе j может быть
настолько велик, что запас 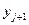 может удовлетворить
спрос всех последующих этапов и при этом не имеет смысла иметь величину запаса
больше суммарного спроса на всех последующих этапах, то переменная
может удовлетворить
спрос всех последующих этапов и при этом не имеет смысла иметь величину запаса
больше суммарного спроса на всех последующих этапах, то переменная  должна удовлетворять ограничениям:
должна удовлетворять ограничениям:
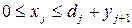
Допустим, что предприятие заключило договора на поставку
своей продукции на четыре месяца. Исходные данные приведены в таблице 9.
При этом исходный запас товара на складе составляет две единицы, т.е 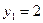 .
.
|
Период k
|
1
|
2
|
3
|
4
|
|
Спрос (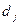 ) )
|
3
|
3
|
2
|
2
|
|
Затраты на производство
|
15
|
19
|
22
|
24
|
|
Затраты на хранение единицы запаса
|
2
|
2
|
2
|
2
|
Предполагается, что
максимальная возможность по производству изделий составляет 4 тыс. единиц.
Положим 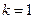 , тогда:
, тогда:
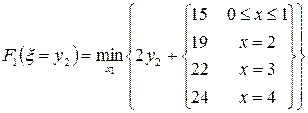
Тогда, т.к. параметр
состояния 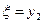 может принимать
значения на отрезке:
может принимать
значения на отрезке:
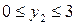
При этом каждому значению
параметра состояния отвечает определенная область изменения переменной 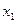 :
:
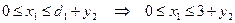
Однако на первом этапе
объем производства не может быть меньше одной единицы, т.к. спрос 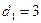 , а исходный запас
, а исходный запас 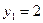 , при этом из балансового уравнения следует, что объем производства
связан с параметром состояния
, при этом из балансового уравнения следует, что объем производства
связан с параметром состояния 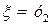 соотношением:
соотношением:
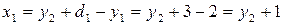
Т.е. каждому значению 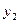 отвечает единственное
значение
отвечает единственное
значение 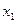 , поэтому:
, поэтому:
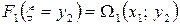 ,
,
Тогда:
Значения
функции состояния 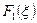 приведены в
таблице 3.1:
приведены в
таблице 3.1:
Таблица 3.1
|
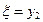
|
0
|
1
|
2
|
3
|
|
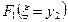
|
15
|
21
|
26
|
30
|
|
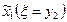
|
1
|
2
|
3
|
4
|
Положим
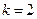 , тогда:
, тогда:
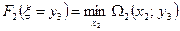 ,
,
Где
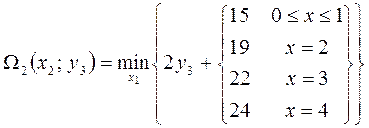
Здесь минимум берется по
переменной 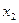 , которая может изменяться в пределах:
, которая может изменяться в пределах:
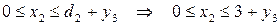
Где верхняя граница
зависит от параметра состояния 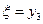 , который принимает значения на отрезке:
, который принимает значения на отрезке:
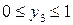
Тогда
при этом из балансового уравнения следует, что остаток товара на начало второго
месяца 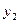 связан с объемом
производства
связан с объемом
производства 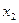 и с параметром состояния
и с параметром состояния
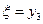 соотношением:
соотношением:

Тогда:
Эти значения
указываем в результирующей таблице 3.2.
Таблица 3.2
Теперь
положим, что 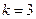 , тогда:
, тогда:
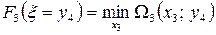 ,
,
Где
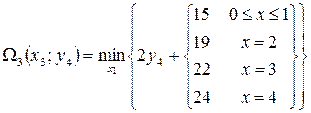
Здесь минимум берется по
переменной 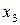 , которая может изменяться в пределах:
, которая может изменяться в пределах:
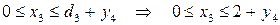
Где верхняя граница
зависит от параметра состояния 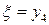 , который принимает значения на отрезке:
, который принимает значения на отрезке:
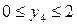
Т.е. 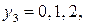 при этом из балансового уравнения следует, что остаток
товара на начало второго месяца
при этом из балансового уравнения следует, что остаток
товара на начало второго месяца 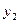 связан с объемом
производства
связан с объемом
производства 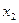 и с параметром
состояния
и с параметром
состояния 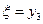 соотношением:
соотношением:
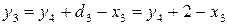
Тогда:
Таблица 3.3
Если
оставлять продукцию к концу четвертого периода не нужно, тогда параметр
состояния принимает единственное значение  , следовательно, переменная
, следовательно, переменная 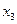 может изменяться в
пределах:
может изменяться в
пределах:
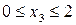
Из балансового уравнения следует, что остаток товара на начало третьего
месяца 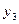 связан с объемом
производства соотношением:
связан с объемом
производства соотношением:
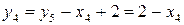
Тогда:
Следовательно,
получаем:
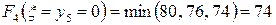
Причем минимум
достигается при 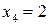 , т.е.:
, т.е.:
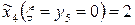
Таким образом, получили
минимальные общие затраты на производство и хранение продукции и последнюю
компоненту оптимального решения:
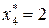
Для нахождения остальных
компонент оптимального решения, необходимо воспользоваться обычными правилами
динамического программирования.
Тогда т.к. 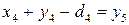 , то
, то 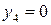 , следовательно, из таблицы 3.3:
, следовательно, из таблицы 3.3:
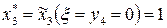
Аналогично
т.к. 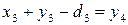 , то
, то 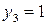
Из таблицы
3.2:
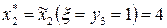
Аналогично т.к. 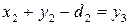 , то
, то 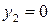
Из таблицы 3.1:
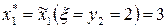
Следовательно,
получен оптимальный план производства:
Задача 4
На сетевом графике (рис
4.1) цифры у стрелок показывают: в числителе – продолжительность работы в днях,
в знаменателе – количество ежедневно занятых работников на её выполнение.
В распоряжении
организации, выполняющей этот комплекс работ, имеется 23 рабочих, которых
необходимо обеспечить непрерывной и равномерной работой.
Используя имеющиеся
запасы времени по некритическим работам, скорректируйте сетевой график с учетом ограничения по
количеству рабочих.
Рис 4.1 Сетевой график
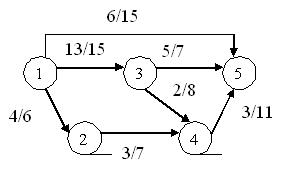
Решение:
Для оптимизации, прежде
всего необходимо рассчитать основные параметры
сетевого графика, чтобы знать, какими резервами располагают
некритические работы и какие работы образуют критический путь.
Ранний срок свершения
исходного события СГ принимается равным
нулю. Ранний срок свершения данного
промежуточного события рассчитывается
путем сравнения сумм, состоящих из раннего
срока свершения события, непосредственно предшествующего данному, и ожидаемой продолжительности. В качестве
раннего срока свершения события принимается максимальная из сравниваемых сумм.
Рассчитанный таким
способом ранний срок свершения завершающего события всего СГ принимается в
качестве его же позднего срока
свершения. Это означает, что завершающее событие СГ никаким резервом времени не располагает.
Поздний срок свершения
данного промежуточного события
определяется при просмотре СГ в обратном направлении. Для этого
сопоставляются разности между поздним сроком свершения события, непосредственно следующего за
данным, и продолжительности работы, соединяющей
соответствующее событие с данным. Так как ни одна из непосредственно следующих за данным
событием работ не
может начаться, пока не свершится
само данное событие, очевидно, его поздний срок свершения равен минимуму из
подсчитанных разностей.
Правильность расчета
поздних сроков свершения
событий СГ подтверждается
получением нулевого позднего срока
свершения исходного события.
Резерв времени образуется
у тех событий, для которых поздний срок
свершения больше раннего, и он равен их разности. Если же эти сроки равны, событие резервом времени не
располагает и, следовательно, лежит
на критическом пути.
В таблице 4.1 приводится
расчет параметров сетевого графика.
Таблица 4.1 Расчет
параметров сетевого графика
|
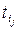
|
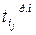
|

|
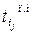
|
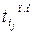
|
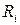
|
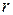
|
|
1-2
|
4
|
0
|
4
|
9
|
13
|
9
|
0
|
|
1-3
|
13
|
0
|
13
|
0
|
13
|
0
|
0
|
|
1-5
|
6
|
0
|
6
|
12
|
18
|
12
|
24
|
|
2-4
|
3
|
4
|
7
|
12
|
15
|
8
|
8
|
|
2-3
|
0
|
4
|
4
|
13
|
13
|
9
|
9
|
|
3-4
|
2
|
13
|
15
|
13
|
15
|
0
|
0
|
|
3-5
|
5
|
13
|
18
|
13
|
18
|
0
|
12
|
|
4-5
|
3
|
15
|
18
|
15
|
18
|
0
|
12
|
На основе данных о
продолжительностях работ и частных резервах времени построим линейный
календарный план работ по ранним началам некритических работ (таблица 4.2).
Просуммировав число рабочих на каждый день по всем работам, построим график
движения рабочих, из которого видно, что он испытывает значительные колебания.
Следовательно, сетевой график с точки зрения использования рабочих составлен не
удовлетворительно и должен быть скорректирован с учетом имеющихся ограничений
по числу рабочих. Пользуясь имеющимися запасами времени по некритическим
работам, изменим их продолжительность, передвинув их начала или сделав то и
другое с таким расчетом, чтобы суммарное число на каждый день составило не
более 23 человек.
Таблица 4.2 Календарный
план до корректировки
|
Код
работы
|
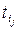
|
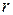
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
|
1-2
|
4
|
0
|
6
|
6
|
6
|
6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1-3
|
13
|
0
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
|
|
|
|
|
|
|
|
|
|
1-5
|
6
|
24
|
15
|
15
|
15
|
15
|
15
|
15
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2-3
|
0
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2-4
|
3
|
8
|
|
|
|
|
7
|
7
|
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3-4
|
2
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8
|
8
|
|
|
|
|
|
|
|
|
3-5
|
5
|
12
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
|
7
|
7
|
7
|
7
|
|
|
|
|
|
4-5
|
3
|
12
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11
|
11
|
11
|
|
|
|
|
|
Число
рабочих до корректировки
|
36
|
36
|
36
|
36
|
37
|
37
|
22
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
18
|
18
|
18
|
|
|
|
|
Таблица 4.3 Календарный
план после корректировки
|
Код
работы
|
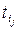
|
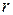
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
|
1-2
|
4
|
0
|
6
|
6
|
6
|
6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1-3
|
13
|
0
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
15
|
|
|
|
|
|
|
|
|
|
|
1-5
|
6
|
24
|
|
|
|
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
|
2-3
|
0
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2-4
|
3
|
8
|
|
|
|
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
|
|
|
|
|
|
|
|
|
|
|
|
3-4
|
2
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8
|
8
|
|
|
|
|
|
|
|
|
3-5
|
5
|
12
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
|
7
|
7
|
7
|
7
|
|
|
|
|
|
4-5
|
3
|
12
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11
|
11
|
11
|
|
|
|
|
|
Число
рабочих после корректировки
|
21
|
21
|
21
|
21
|
23
|
23
|
23
|
23
|
23
|
23
|
23
|
20
|
20
|
20
|
20
|
23
|
23
|
23
|
5
|
5
|
5
|
5
|