Задача №30
Для
производства различных изделий А и В используются три вида сырья. На
изготовление единицы изделия А требуется затратить сырья первого вида 10кг.,
сырья второго вида 5кг., сырья третьего вида 4кг. На изготовление единицы
изделия В требуется затратить сырья первого вида 9кг., сырья второго вида
11кг., сырья третьего вида 15кг.
Производство
обеспечено сырьём первого вида в количестве 1870кг., сырьём второго вида в
количестве 1455кг., сырьём третьего вида в количестве 1815кг. Прибыль от
реализации единицы готового изделия А составит 7руб., а изделия В 9руб.
Составить
план производства изделий А и В, обеспечивающий максимальную прибыль от их
реализации.
Решить задачу
симплексным методом путём преобразования симплекс-таблиц.
Дать
графическое решение задачи.
Решение:
Формализуем
условия задачи: обозначим количество единиц произведённого товара А за х,
товара В – за у. Тогда требуется максимизировать функцию w=7х+9у при следующих ограничениях:
10х+9у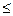 1870 (ограничения по количеству сырья 1-ого вида)
1870 (ограничения по количеству сырья 1-ого вида)
5х+11у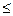 1455 (ограничения по количеству сырья 2-ого вида)
1455 (ограничения по количеству сырья 2-ого вида)
4х+15у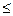 1815 (ограничения по количеству сырья 3-его вида)
1815 (ограничения по количеству сырья 3-его вида)
х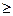 0 (естественные ограничения на единицы товара)
0 (естественные ограничения на единицы товара)
у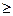 0
0
Перепишем
полученную задачу линейного программирования в канонической форме:
-7х-9у -> min (ЗЛП
в канонической форме – задача на минимум, найдя минимум данной функции, мы
найдём максимум требуемой величины - прибыли)
Ограничения –
равенства => вводим дополнительные переменные a, b, c 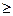 0, такие что
0, такие что
10х+9у+а=1870
5х+11у+b=1455
4х+15у+c=1815
Выбираем в
качестве базисных переменных a,b,c, т.к. соответствующие им столбцы в
матрице ограничений линейно независимы. Записываем симплекс-таблицу:
|
|
x
|
y
|
a
|
b
|
c
|
|
w
|
0
|
-7
|
-9
|
0
|
0
|
0
|
|
a
|
1870
|
10
|
9
|
1
|
0
|
0
|
|
b
|
1455
|
5
|
11
|
0
|
1
|
0
|
|
c
|
1815
|
4
|
15
|
0
|
0
|
1
|
Эта таблица
прямо, но не двойственно допустима => для нахождения оптимального решения
надо сделать преобразование базиса: выбираем первый столбец таблицы, отношение
1870/10 минимально среди 1455/5 и 1815/4 => в качестве ведущего выбираем
элемент (1,1). Делаем замену базиса, получим:
|
|
x
|
y
|
a
|
b
|
c
|
|
w
|
1309
|
0
|
-2.7
|
0.7
|
0
|
0
|
|
x
|
187
|
1
|
0.9
|
0.1
|
0
|
0
|
|
b
|
520
|
0
|
6.5
|
-0.5
|
1
|
0
|
|
c
|
1067
|
0
|
11.4
|
-0.4
|
0
|
1
|
В нулевой строке по-прежнему есть
отрицательный элемент, значит, решение не оптимально. Снова делаем
преобразование базиса: ведущий элемент (2,2) (аналогично выбираем минимальное
среди отношений 187/0.9 520/6.5 и 1067/11.4, минимальное - 520/6.5)
|
|
x
|
y
|
a
|
b
|
c
|
|
w
|
1525
|
0
|
0
|
32/65
|
27/65
|
0
|
|
x
|
115
|
1
|
0
|
11/65
|
-9/65
|
0
|
|
y
|
80
|
0
|
1
|
-1/13
|
2/13
|
0
|
|
c
|
155
|
0
|
0
|
31/65
|
-114/65
|
1
|
Итак,
получили прямо и двойственно допустимую таблицу, а значит, значения х=115 и
у=80 оптимальны.
Ответ: план
производства, обеспечивающий максимальную прибыль, таков: требуется произвести
115 единиц товара А и 80 единиц товара В.
Графическое решение:

|
Линия уровня целевой
функции
|
|
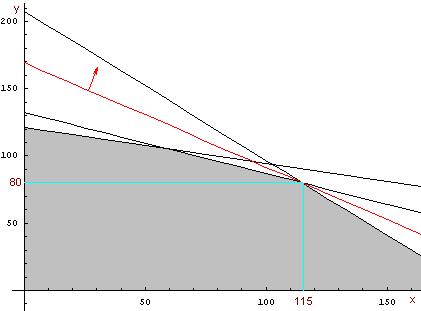
Серым
заполнена область, в которой лежат все наши допустимые решения, т.е. те,
которые удовлетворяют ограничениям задачи. Красным цветом выделена линия уровня
целевой функции, стрелкой указано направление роста целевой функции (вектор
градиента). Смещая линию уровня в указанном направлении, мы увеличиваем
значение целевой функции. При этом, дойдя до крайней точки закрашенного
множества, мы получим максимальное допустимое ограничениями значение целевой
функции. Соответствующие значения x=115, y=80,
что подтверждает решение, полученное симплекс-методом.
Задача №33.
На трёх базах
А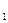 , А
, А , А
, А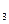 имеется однородный
груз в количестве 250т. на А
имеется однородный
груз в количестве 250т. на А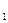 , 200т. на А
, 200т. на А и 150т. на А
и 150т. на А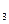 . Полученный груз требуется перевезти в пять пунктов: 180т. в
В
. Полученный груз требуется перевезти в пять пунктов: 180т. в
В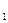 , 120т в В
, 120т в В , 90т. в В
, 90т. в В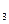 , 105т. в В
, 105т. в В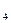 и 105т. в В
и 105т. в В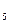 .
.
Затраты на
перевозку груза между пунктами поставок и потребления заданы матрицей тарифов
С:
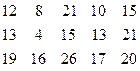
Спланировать
перевозки так, чтобы их общая стоимость была минимальной.
Решение:
Составляем транспортную таблицу
(в левом нижнем углу каждой ячейки указано количество транспортируемого груза,
в правом верхнем – тариф на транспортировку одной тонны груза):
|
В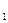
|
В
|
В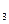
|
В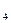
|
В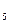
|
|
|
А
|
12
180
|
8
70
|
21
|
10
|
15
|
250
|
|
А
|
13
|
4
50
|
15
90
|
13
60
|
21
|
200
|
|
А
|
19
|
16
|
26
|
17
45
|
20
105
|
150
|
|
180
|
120
|
90
|
105
|
105
|
|
Мы получили
опорный план методом северо-западного угла. Для поиска оптимального плана
пользуемся методом потенциалов.
Составим систему уравнений для
нахождения потенциалов решения, найдем сумму соответствующих потенциалов для
каждой свободной ячейки и пересчитаем тарифы транспортировки для каждой
свободной ячейки (d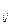 =c
=c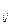 -(a
-(a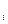 +b
+b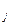 )).
)).
a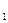 + b
+ b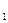 = c
= c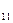 =12 a
=12 a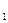 =0 d
=0 d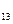 =2
=2
a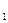 + b
+ b = c
= c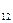 =8 b
=8 b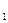 =12 d
=12 d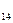 =-7
=-7
a + b
+ b = c
= c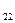 =4 b
=4 b =8 d
=8 d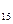 =-5
=-5
a + b
+ b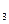 = c
= c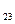 =15 a
=15 a =-4 d
=-4 d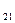 =5
=5
a + b
+ b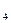 = c
= c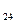 =13 b
=13 b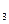 =19 d
=19 d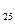 =5
=5
a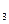 + b
+ b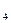 = c
= c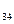 =17 b
=17 b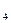 =17 d
=17 d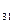 =7
=7
a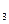 + b
+ b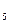 = c
= c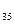 =20 a
=20 a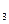 =0 d
=0 d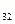 =8
=8
b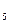 =20 d
=20 d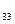 =7
=7
Так как у нас получились
отрицательные значения, то полученный план не является оптимальным. Выберем
ячейку для пересчета 14. Производим пересчёт:
|
В
|
В
|
В
|
В
|
В
|
|
|
А
|
12
180
|
- 8
70
|
21
|
+ 10
|
15
|
250
|
|
А
|
13
|
+ 4
50
|
15
90
|
- 13
60
|
21
|
200
|
|
А
|
19
|
16
|
26
|
17
45
|
20
105
|
150
|
|
180
|
120
|
90
|
105
|
105
|
|
Прокомментируем
пересчёт:
Цикл пересчёта
таблицы - это
последовательность ячеек, удовлетворяющая условиям:
1.
одна ячейка пустая, все остальные занятые;
2.
любые две соседние ячейки находятся в одной строке или в
одном столбце;
3.
никакие три соседние ячейки не могут быть в одной строке
или в одном столбце.
Пустой ячейке присваиваем знак +, остальным поочерёдно знаки - и +. Далее выбираем в минусовых ячейках минимальное
количество транспортируемого груза и прибавляем его к соответствующим ячейкам
со знаком +, вычитаем из ячеек со знаком -. В итоге получим:
|
В
|
В
|
В
|
В
|
В
|
|
|
А
|
12
180
|
- 8
10
|
21
|
+ 10
60
|
15
|
250
|
|
А
|
13
|
+ 4
110
|
15
90
|
- 13
0
|
21
|
200
|
|
А
|
19
|
16
|
26
|
17
45
|
20
105
|
150
|
|
180
|
120
|
90
|
105
|
105
|
|
Проверим план
на оптимальность. Для этого снова составим систему для нахождения потенциалов и
расчёта тарифов:
a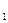 + b
+ b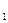 = c
= c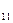 =12 a
=12 a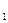 =0 d
=0 d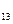 =2
=2
a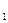 + b
+ b = c
= c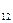 =8 b
=8 b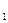 =12 d
=12 d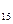 =2
=2
a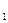 + b
+ b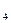 = c
= c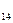 =10 b
=10 b =8 d
=8 d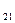 =5
=5
a + b
+ b = c
= c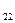 =4 b
=4 b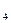 =10 d
=10 d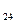 =7
=7
a + b
+ b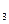 = c
= c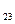 =15 a
=15 a =-4 d
=-4 d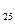 =12
=12
a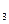 + b
+ b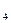 = c
= c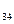 =17 b
=17 b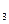 =19 d
=19 d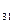 =0
=0
a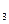 + b
+ b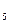 = c
= c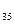 =20 a
=20 a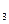 =7 d
=7 d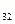 =1
=1
b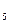 =13 d
=13 d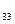 =0
=0
Полученный
план является оптимальным, т.к. все d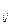
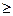 0.
0.
Таким
образом, мы построили план перевозок (указали количество грузов – в правом
нижнем углу каждой ячейки - и базы, на которые эти грузы нужно перевезти – сами
ячейки) так, чтобы их стоимость была минимальной.