Министерство образования Российской Федерации
Всероссийский
заочный финансово-экономический институт
Кафедра математики
и информатики
Аудиторная
работа
по
дисциплине «Эконометрика»
Вариант № 5
Выполнила студентка 3 курса
2 потока 1 подгруппы
Факультет: «ФиК»
Специальность: «ФиК»
№ зачетной книжки:
05ФФД40419
Бадретдинова А.Н.
Руководитель: Фархиева
С.А.
Уфа 2007
Условие:
В таблице 1 представлены данные о
средней ожидаемой продолжительности жизни от нескольких факторов по данным за 1995 г.
Таблица 1
|
Страна
|
У
|
Х2
|
Х3
|
Х4
|
|
Буркина-Фасо
|
49
|
2,8
|
2,1
|
99
|
|
Мадагаскар
|
52
|
3,1
|
3,1
|
99
|
|
Бангладеш
|
58
|
1,6
|
2,1
|
79
|
|
Гаити
|
57
|
2,0
|
1,7
|
72
|
|
Мали
|
50
|
2,9
|
2,7
|
123
|
|
Нигерия
|
53
|
2,9
|
2,8
|
80
|
|
Кения
|
58
|
2,7
|
2,7
|
58
|
|
Тога
|
56
|
3,0
|
2,8
|
88
|
|
Индия
|
62
|
1,8
|
2,0
|
68
|
|
Бенин
|
50
|
2,9
|
2,5
|
95
|
|
Никарагуа
|
68
|
3,1
|
4,0
|
46
|
|
Гана
|
59
|
2,8
|
2,7
|
73
|
|
Ангола
|
47
|
3,1
|
2,8
|
124
|
|
Пакистан
|
60
|
2,9
|
3,3
|
90
|
|
Мавритания
|
51
|
2,5
|
2,7
|
96
|
|
Зимбабве
|
57
|
2,4
|
2,2
|
55
|
|
Гондурас
|
67
|
3,0
|
3,8
|
45
|
|
Китай
|
69
|
1,1
|
1,1
|
34
|
|
Камерун
|
57
|
2,9
|
3,1
|
56
|
|
Конго
|
51
|
2,9
|
2,6
|
90
|
|
Шри-Ланка
|
72
|
1,3
|
2,0
|
16
|
Принятые в таблице
обозначения:
у - средняя ожидаемая
продолжительность жизни при рождении, лет;
Х2 - темпы прироста населения по
сравнению с предыдущим годом, %;
Х3 - темпы прироста рабочей силы по
сравнению с предыдущим годом, %;
Х4 - коэффициент младенческой
смертности, %.
Задание:
1. Построить матрицу
парных коэффициентов корреляции, оценить статистическую значимость
коэффициентов корреляции. Установить, какие факторы коллинеарные.
2. Постройте уравнение
множественной регрессии, обосновав отбор факторов.
3. Построить графики
остатков. Сделать выводы
4. Проверить выполнение
предпосылок МНК.
5. Оцените статистическую
значимость уравнения множественной регрессии. Какие факторы значимо
воздействуют на формирование средней ожидаемой продолжительности жизни в этом
уравнении?
6. Постройте уравнение
множественной регрессии только со статистически значимыми факторами.
7. Рассчитайте прогнозное
значение результата, если прогнозные значения факторов составляют 80% от их
максимальных значений.
8. Рассчитайте ошибки и
доверительный интервал прогноза для уровня значимости 5 или 10% (а=0,05; а =0,10).
Решение:
1) Построим
матрицу парных коэффициентов корреляции с использованием инструмента
Корреляция (Анализ данных в EXCEL).
Для проведения
корреляционного анализа выполните следующие действия:
1.
Данные для корреляционного анализа должны располагаться в смежных диапазонах ячеек.
2. Выберем команду Сервис => Анализ данных.
3.
В диалоговом окне Анализ данных выберем инструмент Корреляция, а затем
щелкните на кнопке ОК.
4.
В диалоговом окне Корреляция в поле Входной интервал необходимо ввести
диапазон ячеек, содержащих исходные данные. Если выделены и заголовки столбцов,
то установите флажок Метки в первой строке.
5.
Выберем параметры вывода
6. ОК.
Таблица 2
|
|
У
|
Х2
|
Х3
|
Х4
|
|
У
|
1
|
|
|
|
|
Х2
|
-0,541
|
1
|
|
|
|
Х3
|
-0,030
|
0,794
|
1
|
|
|
Х4
|
-0,899
|
0,546
|
0,136
|
1
|
Анализ матрицы
коэффициентов парной корреляции показывает, что зависимая переменная У коллинеарная
с фактором Х4 (ryx1= -0,899).
2) Построим уравнение множественной регрессии с применением инструмента Регрессия (Анализ
данных в EXCEL).
Для проведения
регрессионного анализа выполните следующие действия:
1. Выберем команду Сервис => Анализ
данных.
2. В диалоговом окне Анализ данных выберем
инструмент Регрессия, а затем щелкнем на кнопке ОК.
3. В диалоговом окне Регрессия в поле
Входной интервал Y вводим адрес одного
диапазона ячеек, который представляет зависимую переменную. В поле Входной
интервал X вводим адреса диапазонов,
которые содержат значения независимых переменных (рис. 2).
4. Установите флажок Метки в первой строке.
5. Выберите параметры вывода $B$67
6. В поле Остатки поставим необходимые флажки.
7. ОК.
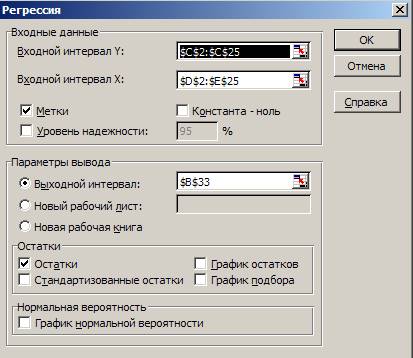
Рис.
2
Диалоговое окно Регрессия подготовлено к выполнению анализа данных
Результат регрессионного анализа содержится в
таблицах на рисунке 3. Рассмотрим содержание этих таблиц.
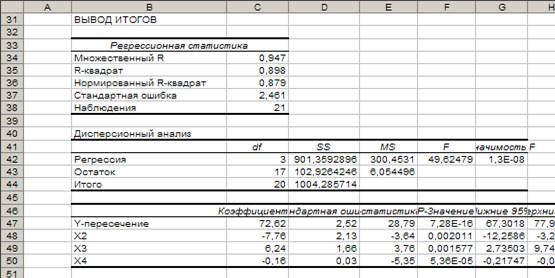
Рис.3
Регрессионный анализ
Во
втором столбце таблицы 3 рисунка 3 содержатся коэффициенты уравнения регрессии
а0, а2, а3 а4. В третьем столбце
содержатся стандартные ошибки коэффициентов уравнения регрессии, а в четвертом
– t – статистика, используемая для
проверки значимости коэффициентов уравнения регрессии.
Уравнение регрессии
зависимости у развития от х1 можно записать в следующем виде:
у = 72,6 -7,76Х2 + 6,24Х3 –
0,16 Х4
3)
Построим графики
остатков.
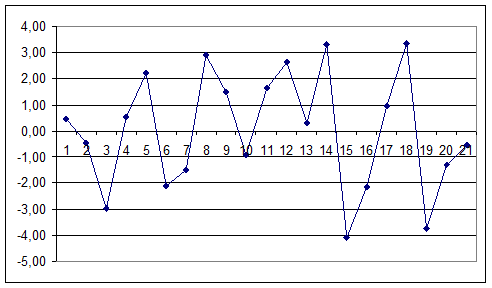
Рис. 4. График остатков
Расчетное значение критерия пиков
равно:
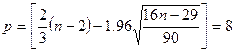
Из графика остатков видно, что
количество поворотных точек равно 11, что больше критического числа поворотных точек. Модель
по этому критерию адекватна. Тренд существует
4)
Проверим выполнение
предпосылок МНК.
Проверка гипотезы о близости к нулю математического
ожидания остатков.
|
Наблюдение
|
Предсказанное У
|
Остатки
|
|
1
|
48,56
|
0,44
|
|
2
|
52,47
|
-0,47
|
|
3
|
60,99
|
-2,99
|
|
4
|
56,48
|
0,52
|
|
5
|
47,79
|
2,21
|
|
6
|
55,12
|
-2,12
|
|
7
|
59,47
|
-1,47
|
|
8
|
53,09
|
2,91
|
|
9
|
60,53
|
1,47
|
|
10
|
50,90
|
-0,90
|
|
11
|
66,35
|
1,65
|
|
12
|
56,36
|
2,64
|
|
13
|
46,70
|
0,30
|
|
14
|
56,68
|
3,32
|
|
15
|
55,10
|
-4,10
|
|
16
|
59,15
|
-2,15
|
|
17
|
66,04
|
0,96
|
|
18
|
65,65
|
3,35
|
|
19
|
60,73
|
-3,73
|
|
20
|
52,31
|
-1,31
|
|
21
|
72,52
|
-0,52
|
|
Сумма
|
|
0,00
|
Легко из представленной
таблицы убедится, что математическое ожидание ряда остатков равно нулю, т.е. |еср| = 0. Модель по этому
критерию адекватна.
Соответствие
ряда остатков нормальному закону
распределения определим
при помощи R/S–критерию с критическими уровнями 2,7 – 3,7.
|
|
E(t) - E(t-1)
|
(E(t) - E(t-1))2
|
E(t)2
|
|
1
|
|
|
0,19
|
|
2
|
-0,91
|
0,83
|
0,22
|
|
3
|
-2,52
|
6,36
|
8,96
|
|
4
|
3,51
|
12,32
|
0,27
|
|
5
|
1,70
|
2,88
|
4,90
|
|
6
|
-4,33
|
18,74
|
4,47
|
|
7
|
0,64
|
0,41
|
2,17
|
|
8
|
4,38
|
19,21
|
8,46
|
|
9
|
-1,44
|
2,08
|
2,15
|
|
10
|
-2,37
|
5,62
|
0,82
|
|
11
|
2,55
|
6,50
|
2,71
|
|
12
|
1,00
|
0,99
|
6,98
|
|
13
|
-2,34
|
5,49
|
0,09
|
|
14
|
3,03
|
9,15
|
11,04
|
|
15
|
-7,42
|
55,13
|
16,82
|
|
16
|
1,95
|
3,81
|
4,62
|
|
17
|
3,11
|
9,68
|
0,93
|
|
18
|
2,39
|
5,70
|
11,22
|
|
19
|
-7,08
|
50,12
|
13,91
|
|
20
|
2,42
|
5,87
|
1,71
|
|
21
|
0,79
|
0,62
|
0,27
|
|
итого
|
|
|
102,9
|
Среднеквадратическое
отклонение: Sе = 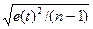 =
= 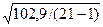 = 2,27
= 2,27
R/S = (мах e(t) - min
e(t) ) / Sе = (3,35 – (-4,1))/2,27 = 3,3
Расчетное значение
попадает в интервал (2,7 …3,7), следовательно, свойство нормальности
распределения выполняется. Модель по этому критерию адекватна.
5) Оценим статистическую значимость уравнения множественной
регрессии.
Рассчитаем параметры линейного
уравнения множественной регрессии.
Оценка
параметров регрессии осуществляется по методу наименьших квадратов по формуле
2, используя данные, приведенные в таблице 3.
А
= (ХтХ)-1 Хт Y
(2)
где а – подлежащий оцениванию вектор неизвестных параметров
размерности (m+1)×1;
Х – матрица n наблюдений
независимых переменных Х1, Х2, …, Хm,
размерность матрицы Х равна n× (m+1);
Y – вектор зависимой переменной размерности n×1,
представляющий собой n наблюдений значений yi.
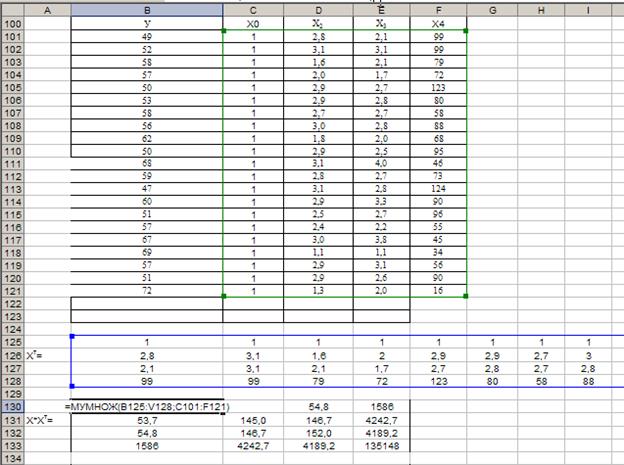
Таблица 3
|
У
|
Х0
|
Х2
|
Х3
|
Х4
|
|
49
|
1
|
2,8
|
2,1
|
99
|
|
52
|
1
|
3,1
|
3,1
|
99
|
|
58
|
1
|
1,6
|
2,1
|
79
|
|
57
|
1
|
2,0
|
1,7
|
72
|
|
50
|
1
|
2,9
|
2,7
|
123
|
|
53
|
1
|
2,9
|
2,8
|
80
|
|
58
|
1
|
2,7
|
2,7
|
58
|
|
56
|
1
|
3,0
|
2,8
|
88
|
|
62
|
1
|
1,8
|
2,0
|
68
|
|
50
|
1
|
2,9
|
2,5
|
95
|
|
68
|
1
|
3,1
|
4,0
|
46
|
|
59
|
1
|
2,8
|
2,7
|
73
|
|
47
|
1
|
3,1
|
2,8
|
124
|
|
60
|
1
|
2,9
|
3,3
|
90
|
|
51
|
1
|
2,5
|
2,7
|
96
|
|
57
|
1
|
2,4
|
2,2
|
55
|
|
67
|
1
|
3,0
|
3,8
|
45
|
|
69
|
1
|
1,1
|
1,1
|
34
|
|
57
|
1
|
2,9
|
3,1
|
56
|
|
51
|
1
|
2,9
|
2,6
|
90
|
|
72
|
1
|
1,3
|
2,0
|
16
|
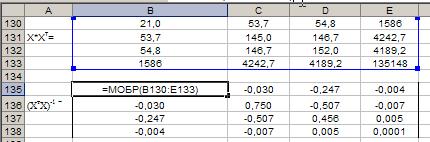
Произведение
матриц ХтХ получаем с помощью функции
=МУМНОЖ(B125:V128;C101:F121). Обратную матрицу определяем с помощью встроенной
функции =МОБР(B120:D122).
|
887,0
|
|
ХтУ =
|
2345,1
|
|
2352,6
|
|
73027
|
|
7,99
|
|
А = (ХтХ)-1
Хт Y=
|
-6,62
|
|
6,53
|
|
0,45
|
Уравнение регрессии
зависимости цены квартиры от 8 факторов можно записать в следующем виде:
у = 7,99 – 6,62Х2 + 6,53Х3 +
0,45 Х4
Значимость
коэффициентов уравнения регрессии а0, а2, а3, а4 оценим с
использованием t-критерия Стьюдента.

 taj = aj/Saj = aj/Se x
taj = aj/Saj = aj/Se x 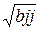 ,
,
|
1,051
|
-0,030
|
-0,247
|
-0,004
|
|
(ХтХ)-1 =
|
-0,030
|
0,750
|
-0,507
|
-0,007
|
|
-0,247
|
-0,507
|
0,456
|
0,005
|
|
-0,004
|
-0,007
|
0,005
|
0,0001
|
b11 = 1,051
b22 = 0,750
b33 = 0,456
b44 = 0,0001
ta0 = 72,6 /2,5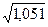 = 28,8
= 28,8
ta2 = -7,76/2,5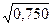 = -3,64
= -3,64
ta3 = 6,24/2,5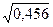 = 3,76
= 3,76
ta4 = -0,16/2,5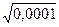 = -5,35
= -5,35
Расчетные значения t-критерия
Стьюдента для коэффициентов уравнения регрессии приведены в четвертом столбце
таблицы 13 протокола EXCEL. Табличное значение t-критерия
Стьюдента можно найти с помощью функции СТЬЮДРАСПОБР (рис. 5).
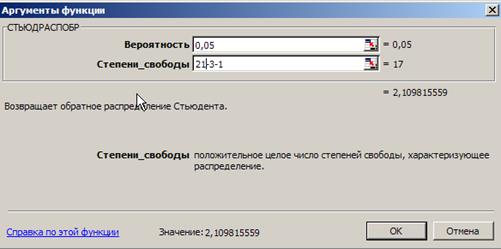
Рис. 5. Определение
табличного значения t-критерия Стьюдента
Табличное значение t-критерия
при 5% уровне значимости и степенях свободы (21 -3 -1 = 17) составляет 2,1.
Так как |tрасп|>tтабл то все коэффициенты существенны
(значимы).
6) Построим
уравнение множественной регрессии со статистически значимыми факторами, т.е.:
у = 7,99 – 6,62Х2 + 6,53Х3 + 0,45
Х4
7) Прогнозное значение результата,
если прогнозное значение факторов составляет 80% от их максимальных значений:
Х2пр = 3,1*0,8 = 2,5
Х3пр = 4,0*0,8 = 3,2
Х4пр = 124*0,8 = 99,2
Yр(N+l) = у = 7,99 – 6,62*2,5 +
6,53*3,2 + 0,45*99,2 = 57,8
8) Для уровня
значимости 5%:
Доверительный
интервал прогноза
будет иметь следующие границы:
Верхняя граница прогноза:
Yр(N+l)+ U(1)
Нижняя граница прогноза: Yр(N+l)- U(1)
U(1)
= Se tкp  =se tкp
=se tкp 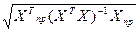
S = 2,5
= 2,5
tкp = 2,2
Хпрт=
(1; 2,5; 3,2; 99,2)
|
1,0514
|
-0,0304
|
-0,2468
|
-0,0037
|
|
(ХтХ)-1 =
|
-0,0304
|
0,7499
|
-0,5072
|
-0,0075
|
|
-0,2468
|
-0,5072
|
0,4563
|
0,0047
|
|
-0,0037
|
-0,0075
|
0,0047
|
0,0001
|
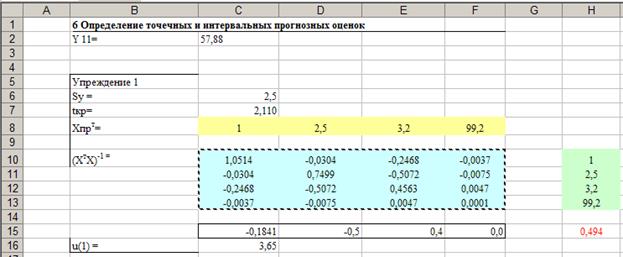
U(1) = 2,5*2,2* 0,494= 3,65
|
Упреждение
|
Прогноз
|
Нижняя граница
|
Верхняя граница
|
|
1
|
57,88
|
54,23
|
61,53
|
Для уровня значимости 10%:
Доверительный
интервал прогноза
будет иметь следующие границы:
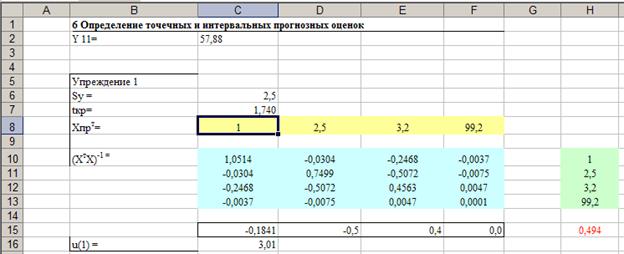
U(1) = 2,5*1,74* 0,494 = 3,01
|
Упреждение
|
Прогноз
|
Нижняя граница
|
Верхняя граница
|
|
1
|
57,88
|
54,87
|
60,89
|