Задача № 8
Определить изменение изобарно-изотермического потенциала при
стандартных условиях для реакции
2HCl(г) + Ca(т) = CaCl2 (т) + H2 (г),
если ΔG0f для HCl(г) = +94,9 кДж/моль, для CaCl2 (т) = +749,5
кДж/моль. Протекает ли этот процесс самопроизвольно?
Решение:
Изобарно-изотермический потенциал реакции рассчитывается по
теплотам образования веществ:
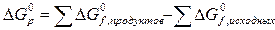
Определим изобарно-изотермического потенциала для данной
реакции, учитывая, что теплоты образования простых веществ равны нулю:
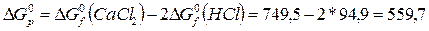 кДж/моль.
кДж/моль.
Поскольку полученное значение ΔG0р > 0, то
процесс самопроизвольно протекать не может.
Ответ: ΔG0р = 559,7 кДж/моль.
Задача № 16
Зависимость скорости химической реакции от температуры,
правило Вант-Гоффа, температурный коэффициент реакции.
Скорость большинства реакций увеличивается с температурой.
Увеличение скорости реакции с температурой описывается уравнением, впервые
предложенным С. Аррениусом, и потому носящим его имя:
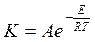 ,
,
или
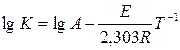
При графическом изображении этого уравнения в виде зависимости
lg К
от Т-1 получается
прямая линия, которая отсекает по оси ординат отрезок, равный lg А, а из тангенса наклона которой
можно определить величину Е, выражаемую в
килоджоулях и называемую энергией активации.
При термической активации для двух температур T1 и Т2
отношение констант скоростей будет:
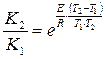
Расчеты с использованием данного теоретического уравнения
подтвердили найденное ранее эмпирическим путем правило о том, что повышение
температуры на 10 градусов увеличивает скорость реакции в 2-4 раза
(приближенное правило Вант - Гоффа). Число, показывающее, во сколько
раз увеличивается скорость реакции (следовательно, и константа скорости) при
увеличении температуры на 10 градусов называется температурным коэффициентом
реакции:
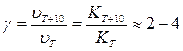
или
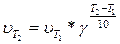 .
.
Это означает, например, что при увеличении температуры на
1000 для условно принятого увеличения средней скорости в 2 раза (γ
= 2) скорость реакции возрастает в 210, т.е. приблизительно в 1000
раз, а при γ = 4 - в 410, т.е. в 1000000 раз. Правило
Вант-Гоффа применимо для реакций, протекающих при сравнительно невысоких
температурах, и для довольно узкого интервала температур. Резкое возрастание
скорости реакции при повышении температуры объясняется тем, что число активных
молекул при этом возрастает в геометрической прогрессии.
Задача № 22
Рассчитать максимальное количество фаз, которые могут существовать
в различных системах, состоящих только из молекул Н2О. Понятие
тройной точки на диаграмме состояния воды.
В соответствии с правилом фаз Гиббса для равновесной
гетерогенной системы число фаз (Ф)
плюс число степеней свободы (С) равно числу компонентов (К) плюс
два
Ф + С = К + 2
В нашем случае система является однокомпонентной, т.е. К =
1. Для однокомпонентной системы имеем: Ф = К + 2 - С = 3 - С. Если число
степеней свободы С равно 2, то система состоит только из одной фазы, например,
вода или водяной пар. При равновесии в однокомпонентной системе с числом
степеней свободы С = 1 количество фаз Ф = 3 – 1 = 2. В качестве примеров таких
систем могут служить системы вода ↔ пар или лед ↔ пар. Наконец,
если система не имеет ни одной степени свободы, то она будет трехфазна, система, в которой
сосуществуют лед, вода и пар.
Для наглядного изображения фазовых равновесий в конкретных
системах используется графический метод. Для этого в простейшем случае
используется прямоугольная система координат, где на оси абсцисс откладывается
абсолютная температура, а на оси ординат - давление. Такое изображение фазовых
равновесий называют фазовой диаграммой или диаграммой состояния. Рассмотрим
диаграмму состояния воды (рис. 1.). Внутри диаграммы наносятся точки, отвечающие
экспериментально найденным значениям Р и Т, характеризующим фазовые
равновесия между двумя фазами. Тогда каждой фазе в однокомпонентной системе
будет отвечать определенное поле на диаграмме, а различные состояния межфазного
равновесия будут расположены на кривой Р = f (T). По
одну сторону от этой кривой система находится только в виде одной фазы, по
другую сторону располагается рассматриваемый компонент в виде второй фазы.
Каждая точка на этой линии характеризует, например, для системы жидкость - пар,
конкретное значение температуры, которой отвечает только одно равновесное
значение давления насыщенного пара жидкости. Тогда, учитывая сказанное ранее,
можно утверждать, что на этой линии число С = 1 и, следовательно, в
соответствии с правилом фаз, независимо можно изменять лишь один параметр.
Отсюда, если изменить Т, то межфазное равновесие сохранится при условии, что Р
самопроизвольно изменится строго определенным образом. Аналогично можно
рассмотреть равновесия для данной однокомпонентной системы между жидкостью и
твердым телом, между твердым телом и паром. В итоге получим совокупность
кривых, которые и образуют диаграмму состояния данного вещества.
|
|
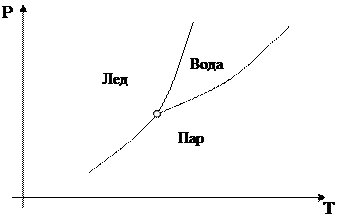 |
Рис. 1. Схематическое изображение диаграммы
состояния воды
Как отмечалось выше для однокомпонентной трехфазной системы по
правилу фаз Гиббса С = 0, т. е. система не имеет ни одной степени свободы.
Действительно, одновременное существование в равновесии жидкого, твердого и
газообразного состояний одного и того же вещества возможно при строго определенных
и температуре, и давлении в так
называемой тройной точке
вещества. Для воды
такой точкой является Т = 0,010С; р = 600 Па.
Задача № 39
Определить осмотическое давление раствора сахара при
температуре 273 К, если при температуре 300 К осмотическое давление этого
раствора равно 800 мм рт. ст.
Решение:
По уравнению Вант – Гоффа: 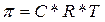 . Для двух температур T1 и Т2 отношение осмотических давлений
будет:
. Для двух температур T1 и Т2 отношение осмотических давлений
будет: 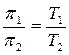 .
.
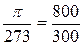 ;
; 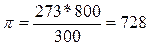 мм рт. ст.
мм рт. ст.
Ответ: π = 728 мм рт. ст.
Задача № 46
Гальванический
элемент, его ЭДС и причина ее возникновения. Схема и принцип работы
гальванического элемента Даниэля – Якоби.
При
протекании окислительно-восстановительных реакций электроны от вещества-восстановителя
переходят к веществу-окислителю. При этом химическая энергия освобождается в
виде теплоты. Если же окислитель отделить от восстановителя каким-либо третьим
раствором электролита и соединить их между собой металлическим проводником, то
тогда реакция восстановления будет протекать на одном конце металлического
проводника, реакция окисления — на другом, а электроны, освобождающиеся при
реакции окисления, будут перетекать по металлу к окислителю. При этом
химическая энергия реакции будет превращаться в электрическую.
Устройство, в котором химическая энергия
самопроизвольно превращается в электрическую, называется химическим
источником тока (ХИТ) или гальваническим элементом. Гальванический элемент
состоит из двух или нескольких соприкасающихся друг с другом растворов
электролитов, в которые погружены металлические пластинки — электроды,
соединенные между собой внешним проводником. Электрод, на котором протекает реакция восстановления, называется
катодом, а электрод, на
котором протекает реакция окисления, — анодом.
Рассмотрим получение электрического тока за счет
следующей пары окислительно-восстановительных систем (гальванический элемент
Даниэля – Якоби):
|
Окисленная
форма
|
|
Восстановленная
форма
|
|
Стандартный
потенциал
|
|
Zn2+ + 2ē
|
=
|
Zn
|
|
-0,76 в
|
|
Cu2+ + 2ē
|
=
|
Cu
|
|
+0,34 в
|
Согласно значениям стандартных потенциалов система Си2+
+ 2ē ↔ Cu по отношению к системе Zn2+ + 2ē ↔ Zn является
окислителем, т.е. при их контакте электроны будут переходить от Zn к
ионам Си2+:
 Zn + Cu2+ = Zn2+ + Cu
Zn + Cu2+ = Zn2+ + Cu
|
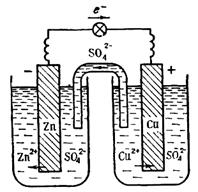
Рис. 2. Схема гальванического элемента
|
Схема данного гальванического элемента изображена на
рис. 2. Он состоит из цинкового и медного электродов, погруженных в 1 н
растворы соответственно ZnSO4 и CuSO4. Сосуды с растворами
соединены U-образной трубкой, заполненной каким-либо электролитом. При
соединении электродов проводом начинается окислительно-восстановительная
реакция. На цинковом электроде (аноде) происходит потеря электронов —
окисление цинка:
Zn - 2ē = Zn2+
на медном электроде (катоде) происходит
присоединение электронов –
восстановление ионов меди:
Cu2+ +
2ē = Cu
За
счет окислительно-восстановительной реакции по внешней цепи (металлический
проводник) течет электрический ток от цинкового электрода к медному, а по
внутренней цепи (трубка с электролитом) движутся ионы SO . Цинковый электрод постепенно растворяется, а на медном
выделяется металлическая медь.
. Цинковый электрод постепенно растворяется, а на медном
выделяется металлическая медь.
Электрический
потенциал катода больше, чем анода. Потенциалы электродов зависят от природы
электродных реакций, концентраций окисленной и восстановленной форм веществ,
участвующих в электродной реакции, и от температуры.
Разность
потенциалов электродов равна напряжению или электродвижущей силе (э.д.с.)
гальванического элемента и в рассматриваемом случае равна
э д.с. = 0,34 - (-0,76) = 1,1 в.
Задача № 53
Классификация
дисперсных систем по размерам дисперсных частиц, агрегатным состояниям
дисперсной фазы и дисперсной среды.
Дисперсные
системы классифицируют по величине частиц дисперсной фазы (степени
дисперсности) и агрегатному состоянию дисперсной фазы и дисперсионной среды.
Количественно
степень дисперсности характеризуется линейными размерами частиц раздробленного
вещества, т.е., чем меньше размеры частиц, тем больше степень дисперсности
фазы. По величине частиц дисперсной фазы все дисперсные системы можно условно
разделить на группы.
1. Грубодисперсные системы. Размер
частиц превышает 0,1 мкм. Это взвеси, суспензии, если дисперсная фаза
состоит из твердых частиц, и эмульсии, если дисперсная фаза состоит из капель
жидкости. Примером суспензии может
служить взмученная глина в воде,
а примером эмульсии - распределение мельчайших капель масла в воде.
Дисперсные
системы, обладающие кинетической устойчивостью, т.е. частицы которых под
влиянием броуновского движения находятся в хаотическом движении, относятся к
коллоидным системам.
2. Коллоидные системы. Размеры
частиц лежат в пределах от 0,1 мкм до 1 ммкм (ммкм—миллимикрон). Такие
частицы уже не оседают, не задерживаются порами бумажного фильтра (проходят
через него, но не проходят через пористые перепонки из животных тканей).
Частицы
коллоидных систем по своим размерам значительно больше молекул (ионов) среды,
что обусловливает наличие поверхности раздела: коллоидная частица - среда. В
суспензиях поверхность раздела можно наблюдать визуально или с помощью
микроскопа, в то время как в коллоидных системах отдельные частицы можно
обнаружить только с помощью специальных оптических приборов.
Коллоидные
системы – это агрегатно-неустойчивые системы. Для создания устойчивости системы
необходимо вводить в нее третий компонент, стабилизирующий ее.
В
отличие от коллоидных систем все молекулярно-ионные растворы относятся к
гомогенным системам; их называют истинными растворами или просто растворами.
3.
Истинные растворы (молекулярно- и ионно-дисперсные системы). Размер частиц
обычно меньше 1 ммкм. К ним относятся растворы солей, кислот, оснований
и др.
Коллоидные
системы по степени дисперсности располагаются между грубыми взвесями. При
уменьшении размеров коллоидных частиц до размеров молекул коллоидные растворы
переходят в истинные.
Классификация
дисперсные системы по агрегатному состоянию
дисперсной фазы и дисперсионной среды представлена в таблице 1.
Таблица 1.
Классификация дисперсные системы по агрегатному состоянию дисперсной фазы и дисперсионной
среды
|
Дисперсионная
среда
|
Дисперсная фаза
|
Название
дисперсной системы
|
Примеры
дисперсных систем
|
|
Жидкость
|
Твердое тело
|
Суспензия, золь
|
Золи металлов,
природные воды
|
|
Жидкость
|
Эмульсия
|
Молоко, нефть
|
|
Газ
|
Пена
|
Мыльная пена
|
|
Твердое тело
|
Твердое тело
|
Минералы, сплавы
|
Рубин, сталь
|
|
Жидкость
|
Пористое тело, минерал
|
Влажный грунт, опал
|
|
Газ
|
Пористое тел
|
Сухой грунт,
активированный уголь,
пенопласт
|
|
Газ
|
Твердое тело
|
Аэрозоль
|
Пыль, дым
|
|
Жидкость
|
Аэрозоль
|
Туман, облака
|
Задача № 70
Рассчитать
число частиц в гидрозоле, если масса дисперсной фазы равна 2 * 10-3
кг, ее плотность – 1,3 * 103 кг/м3, а средний диаметр
частиц 5 * 10-8 м.
Решение:
1.
Определим объем одной частицы (V):
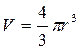 ,
,
где: r – радиус частицы, м; в нашей
задаче он равен 2,5 * 10-8м.
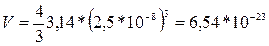 м3.
м3.
2.
Определим число частиц (n) в гидрозоле по формуле:
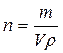 ,
,
где: m – масса дисперсной фазы,
кг;
ρ – плотность дисперсной фазы.
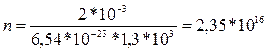
Ответ: n = 2,35 * 1016.
Задача № 77
Адсорбционная
хроматография. Уравнения изотерм адсорбции, их анализ и области применимости.
Адсорбция
из растворов находит важное применение в хроматографическом методе разделения
веществ, открытом русским ученым М. С. Цветом в 1906 г.
|
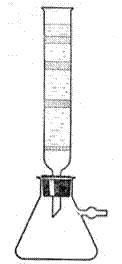
Рис. 3. Хроматографическая колонка
|
В
этом методе адсорбент, например, специально приготовленный оксид алюминия, в
виде порошка помещается в вертикальную стеклянную колонку, где он тщательно
утрамбовывается. Хроматографическая колонка Цвета представлена на рисунке 3. Смесь
веществ, подвергаемая хроматографическому разделению, растворяется в
соответствующем растворителе. Раствор пропускается через колонку, заполненную
адсорбентом. В верхней части колонки адсорбируется компонент, адсорбционная
способность которого наиболее велика. По ходу растворителя сверху колонки вниз
на оксиде алюминия адсорбируются вещества в порядке уменьшения их
адсорбционной способности. Однако полное разделение адсорбируемых компонентов
при этом не достигается. Поэтому после адсорбции компонентов смеси через
колонку пропускается чистый растворитель, что обеспечивает разделение
адсорбированных веществ по слоям, более удаленным друг от друга, иными
словами, достигается более четкое их разделение.
Если
разделению подвергаются окрашенные вещества, то слои адсорбента окрашиваются и
разделены бесцветными промежутками одного адсорбента. Этим методом М. С. Цвет
доказал, что природный хлорофилл состоит из нескольких компонентов. Для
выделения адсорбированных веществ колонка адсорбента может быть целиком или по
частям извлечена из стеклянной трубки и разделена на части, на которых
адсорбирован только один из компонентов смеси. Выделение индивидуальных
адсорбированных компонентов можно осуществить также путем элюирования, т.е.
последовательным вымыванием отдельных слоев адсорбированных веществ, пропуская
соответствующие растворители порциями через колонку. В настоящее время
применяется много вариантов хроматографического метода. В органической химии и
в биохимии широкое применение нашла бумажная хроматография, в которой в
качестве адсорбента применяются полоски из бумаги, специально приготовляемой
для этой цели (хроматографическая бумага). Разработаны также хроматографические
методы разделения газовых смесей, что привело к значительному улучшению методов
газового анализа.
Величина
адсорбции зависит от природы поверхности адсорбента, природы адсорбата и его
концентрации (давления), температуры и др. Графическая зависимость адсорбции от
концентрации адсорбируемого вещества в объемной фазе при данной температуре
называется изотермой адсорбции.
Адсорбция
из предельно разбавленных растворов или смесей газов подчиняется закону Генри:
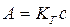 или
или 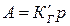
где: А –
величина адсорбции;
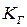 и
и 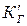 — константа Генри;
— константа Генри;
с — концентрация адсорбата в объемной фазе;
р — давление пара адсорбата.
Аналитическим
выражением изотермы мономолекулярной адсорбции при более высоких концентрациях
и на ровной поверхности является уравнение изотермы Ленгмюра:
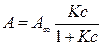 или
или 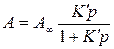
где: 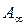 — предельная
мономолекулярная адсорбция -
емкость монослоя;
— предельная
мономолекулярная адсорбция -
емкость монослоя;
К и К' — константы
адсорбционного равновесия, характеризующие энергию адсорбции.
Для
высоких давлений пара изотерма адсорбции описывается общим уравнением обобщенной
теории Ленгмюра — уравнением полимолекулярной адсорбции БЭТ (Брунауэра, Эммета
и Теллера):
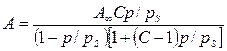
где: С — константа, характеризующая энергию взаимодействия
сконденсированного адсорбата с поверхностью адсорбента;
ps — давление насыщенного пара адсорбата.
Уравнение
Ленгмюра и уравнение БЭТ широко используются для определения удельной
поверхности адсорбентов, катализаторов и других дисперсных систем.
Эмпирическое уравнение Фрейндлиха:
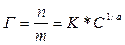
где: Г - величина адсорбции, кмоль/кг (кмоль/м2);
n - количество
вещества-адсорбтива, кмоль;
m - масса адсорбента, кг;
К - константа. При С = 1 кмоль / м3: К = Г;
1/а - константа (адсорбционный показатель) зависит от
природы адсорбента и температуры 1/а = 0,1 - 1.
Это
уравнение хорошо описывает адсорбцию для интервала средних концентраций
растворов (или давлений газа).
Задача № 84
Написать
формулу золя золота Au, стабилизированного KAuO2. У какого из электролитов –
NaCl, Na2SO4, BaCl2, или FeCl3 – порог коагуляции будет
иметь меньшую величину?
Строение
частиц золя золота выражается схемой:
[m (Au) · n AuO2- · (n - x)
K+]x- · x K+
При
электролитной коагуляции по концентрационному механизму (для сильно заряженных
частиц) порог коагуляции ск в соответствии с правилом
Дерягина — Ландау (обоснование эмпирического правила Шульце — Гарди) обратно
пропорционален заряду z противоионов в шестой
степени, т.е.
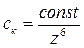
Определим
заряды ионов: NaCl → Na+ + Cl-
Na2SO4
→ 2Na+ + SO42-
BaCl2
→ Ba2+ + 2Cl-
FeCl3
→ Fe3+ + 3Cl-
В
нашем случае, для коагуляции золя золота, частицы которого несут отрицательный
заряд, коагулирующим ионом электролита является катион. Так как коагулирующее
действие электролита возрастает с увеличением заряда иона, знак которого
противоположен знаку заряда коллоидной частицы (как видно из правила Дерягина —
Ландау), то меньшую величину порог коагуляции будет иметь у электролита FeCl3.
Задача № 92
Порог
коагуляции. Правило Шульце – Гарди.
Многочисленные
исследования явления коагуляции показали, что почти все электролиты, взятые в
достаточном количестве, способны коагулировать коллоидные растворы.
Прибавление
к коллоидному раствору электролита влечет за собой увеличение концентрации
противоионов во всех слоях и в том числе в слое адсорбционных (связанных) противоионов,
что ведет к уменьшению дзэта-потенциала.
Связь
мицелл с окружающей их дисперсионной средой при этом уменьшается и наступает
коагуляция. Явная коагуляция наступает, когда концентрация электролита
начинает превышать некоторую минимальную величину Наименьшая концентрация
электролита, вызывающая коагуляцию за определенный промежуток времени и
выраженная в миллимолях на 1 л (ммоль/л),
называется порогом коагуляции
золя данным электролитом.
Коагулирующей
частью электролита является один из его ионов — тот, который несет заряд,
противоположный по знаку заряду коллоидной частицы. Например, для коагуляции
гидрозоля гидроксида железа (III), частицы которого несут
положительный заряд, коагулирующим ионом электролита является его анион.
Величина заряда коагулирующего иона обусловливает порог коагуляции данного
коллоида. При этом величина порога коагуляции тем меньше, чем выше заряд
коагулирующего иона. Другими словами, коагулирующее действие электролита
возрастает с увеличением заряда иона, знак которого противоположен знаку
заряда коллоидной частицы.
В
таблице 2 приведены некоторые данные для двух золей: отрицательно заряженного
сульфида мышьяка — концентрация As2S3 1,85 г/л и положительно заряженного
гидроксида железа (III) — концентрация Fe(ОН)3 0,823 г/л.
Таблица 2.
Коагуляция золей As2S3 и Fe(OH)3 электролитами
|
Золь As2S3
|
Золь Fe(OH)3
|
|
Электролит
|
Коагулирующий ион (катион)
|
Концентрация электролита в
ммоль/л
|
Электролит
|
Коагулирующий ион (анион)
|
Концентрация электролита в
ммоль/л
|
|
NaCl
|
Na+
|
51
|
КСl
|
С1-
|
9,0
|
|
КСl
|
К+
|
49,5
|
КВr
|
Вr-
|
12,5
|
|
MgCl2
|
Mg2+
|
0,72
|
KI
|
I-
|
10,0
|
|
СаСl2
|
Ca2+
|
0,65
|
KNO3
|
NO3-
|
12,0
|
|
ВаСl2
|
Ba2+
|
0,69
|
К2SO4
|
SO42-
|
0,205
|
|
А1Сl3
|
Al3+
|
0,092
|
К2Сг2O7
|
Cr2O72-
|
0,195
|
Таблица
показывает, что коагулирующая способность ионов растет с увеличением заряда,
как это имеет место и при адсорбции их.
Если
коагулирующее свойство иона считать обратно пропорциональным концентрации и
принять коагулирующее действие однозарядного катиона (например, Na+) за единицу, то в отношении
двух- и трехзарядных катионов можно сделать следующее сопоставление: М3+ — 1; М2+ —10-50; М+ —500-1000.
Приведенное
сопоставление указывает на значительный рост коагулирующей способности ионов с
повышением их зарядности.
Таким
образом, коагулирующее действие электролита возрастает с увеличением
зарядности иона, знак заряда которого противоположен знаку коллоидной частицы
— правило значности Шульце — Гарди.
Задача № 103
Студни как эластичные гели. Механизм их образования и
факторы, определяющие скорость студнеобразования. Процессы студнеобразования в
пищевой технологии.
Студни - это ограниченно набухшие полимеры, их можно
рассматривать как частную форму эластичных гелей. Студни - гомогенные системы
и они не тиксотропны. Жидкость,
заполняющая сетку студня, называется интермицеллярной
жидкостью.
Разнообразные способы получения студней могут быть разбиты
на две основные группы: а) желатинирование растворов и б) набухание сухих
веществ (ксерогелей) в соответствующих жидких средах или охлаждение раствора
ВМС.
Процесс перехода раствора в студень называется застудневанием
или желатинированием. Желатинирование — это своеобразная коагуляция, когда
одновременно с дисперсной фазой выпадает в осадок и дисперсионная среда.
Желатинирование происходит в том случае, когда частицы золя сильно связаны с дисперсионной
средой.
Процесс желатинирования можно представить себе следующим
образом. Отдельные, удлиненные мицеллы, сталкиваясь между собой в процессе
кинетического движения, соединяются гидрофобными участками. В результате
образуется рыхлая сетка (каркас), которая охватывает весь объем раствора.
Дисперсионная среда состоит,
вероятнее всего, из молекулярно-дисперсного раствора очень низкой концентрации, что и
приводит систему к потере подвижности. Утрата раствором текучести (не
выливается из опрокинутого сосуда) служит внешним признаком момента образования
студня.
Связи между частицами дисперсной фазы могут также
образовываться за счет взаимодействия полярных и ионизированных групп макромолекул.
Соединение мицелл в сетку может быть настолько непрочно, что достаточно встряхивания,
чтобы произошло разрушение структуры студня и получился раствор, который при стоянии
опять может застыть.
Таким образом, истинное застудневание обусловливается не
слиянием сольватных оболочек коллоидных частиц (лиосфер), а образованием
достаточно прочной внутренней структуры за счет взаимодействия незащищенных
растворителем лиофобных участков мицелл.
На желатинирование оказывают влияние следующие факторы:
концентрация, температура, продолжительность процесса, электролиты,
неоднородность поверхности дисперсных частиц в отношении ее сольватированности,
форма частиц. Застудневание возможно лишь при такой концентрации частиц,
которая достаточна для возникновения структуры. Слишком разбавленные золи и
растворы или застудневают в виде отдельных хлопьев, или совсем не застудневают.
Для некоторых веществ эта величина концентрации очень незначительна. Температура
сильно влияет на застудневание. С понижением температуры уменьшается энергия
теплового движения частиц, поэтому понижение температуры способствует
застудневанию.
Процесс застудневания не совершается мгновенно при достижении
раствором определенной температуры, но требует более или менее продолжительного
времени, необходимого для перегруппировки составных частей в вязкой системе.
Это постепенное застудневание носит название созревания. Оно продолжается и
после того, как уже образовался студень, и выражается в приобретении им большой
механической прочности.
Действие электролитов на растворы ВМС носит сложный характер.
Часто оно вызывает образование связей между молекулами полимера, что приводит к
понижению растворимости соединений.
При застудневании белков большое значение имеет величина рН
среды. Скорость застудневания увеличивается при приближении рН раствора к изоэлектрической
точке, соответствующей одинаковому количеству противоположных зарядов в
молекуле.
Таким образом, факторы, способствующие частичной дегидратации
лиофильных частиц, в большинстве случаев благоприятствуют застудневанию.
Непременным условием застудневания является наличие в коллоидных частицах
одновременно и полярных (защищенных растворителем), и неполярных
(незащищенных) участков.
Действие неэлектролитов на желатинирование высокомолекулярных
соединений весьма специфично. Неэлектролиты, уменьшающие растворимость, обычно
способствуют желатинированию.
Форма частиц играет большую роль в процессах застудневания.
Особенно хорошо желатинируются золи и растворы, образованные лентообразными,
нитевидными частицами.
Желатинирование играет большую роль в технологии искусственного
волокна, некоторых взрывчатых веществ, в кондитерском деле.
Список литературы
1.
Балезин С.А. и др. Основы физической и коллоидной
химии. – М.: «Просвещение», 1985.
2.
Гамеева О.С. Сборник задач и упражнений по физической и
коллоидной химии: Учебное пособие. – М.: Высшая школа, 1980.
3.
Лабораторные работы и задачи по коллоидной химии. / Под
ред. Ю. Г. Фролова. – М.: «Химия», 1986.
4.
Физическая и коллоидная химия: Учебное пособие. / Под
ред. Добычина Д.П. – М.: Просвещение, 1986.
5.
Фридрихсберг Д.А. Курс коллоидной химии: Учебник. – Л.:
Химия, 1984.