Контрольная работа № 4

Контрольная работа № 1.

11–20. Дан треугольник с вершинами K(k_x;k_y), L(l_x;l_y), M(m_x;m_y), Найти:

а) уравнение прямой, содержащей опущенную из вершины L высоту;

б) длину высоты, опущенной из вершины L;

в) точку N, симметричную точке L относительно прямой, проходящей через точки K, M;

г) уравнение прямой, содержащей биссектрису угла L.

20. k_x = –2; k_y = 5; l_x = –3; l_y = 4; m_x = 6; m_y = 9.

Решение.

K(–2;5), L(–3;4), M(6;9).

а) Найдем уравнение стороны KM.

4x+8=8y–40

4x–8y+48=0

x–2y+12=0

Уравнение прямой, перпендикулярной к прямой KM будет иметь вид:

2x+y+C=0

Постоянную С найдем из условия, что искомая прямая проходит через точку L.

2∙(–3)+4+C=0

–6+4+C=0

–2+C=0

C=2

Получаем уравнение прямой, содержащей опущенную из вершины L высоту:

2x+y+2=0

б) Найдем точку N пересечения стороны KM и высоту, проведенной из вершины L.

x=2y–12

4y–24+y+2=0

5y–22=0

y=4.4

x=2·4.4–12 = –3.2

Длина высоты.

в) Обозначим x₀, y₀ – координаты искомой точки P

Т.к. точка N – середина отрезка LP, получаем:

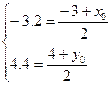
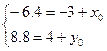
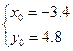
Получили точку P(–3.4;4.8)

г) Для нахождения уравнения биссектрисы LQ достаточно найти направляющий вектор этой прямой, в качестве которого можно взять вектор . Найдем этот вектор.

K(–2;5), L(–3;4), M(6;9).

Так как нас интересует только направление, то направляющий вектор можно умножить на любое число. Умножив координаты вектора на , получим

Искомое уравнение биссектрисы.

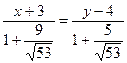
25. Написать общее уравнение плоскости, приходящей через точку K(1;1;–2) параллельно прямым и .

Решение.

Найдем вектор нормали плоскости, параллельной указанным прямым.

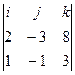= –i+2j+k

Общее уравнение плоскости, имеющей такую нормаль

–x+2y+z+C=0

Значение C найдем из условия, что плоскость проходит через точку K.

–1+2–2+C=0

C=1

Следовательно, искомое уравнение плоскости –x+2y+z+1=0

37. Найти расстояние между параллельными прямыми и

Решение.

Найдем точки пересечения данных прямых с какой-нибудь из плоскостей, нормальных к обоим прямым. Расстояние между точками пересечения и будет расстоянием между прямыми.

Общий вид уравнения плоскости, перпендикулярной данным прямым будет x+y–z+C=0.

Возьмем плоскость x+y–z=0.

Запишем уравнения прямых в параметрической форме.

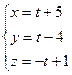
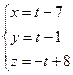
Найдем точки пересечения данных прямых с плоскостью x+y–z=0

Первая прямая.

t+5+t–4+t–1=0

3t=0

t=0

Точка пересечения M(5;–4;1)

Вторая прямая.

t–7+t–1+t–8=0

3t–16=0

Точка пересечения

Расстояние между найденными точками

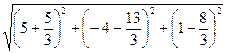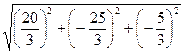= = = = ≈ 10.8

Контрольная работа № 2.

В задачах 51–60 найти пределы:

51. б) = = = = = =

в) = = = = =

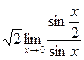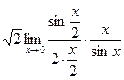г) = = = = = =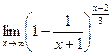

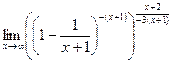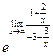В задачах 61–70 вычислить производные.

70. а)

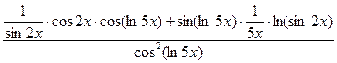
б) = =

= = =

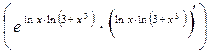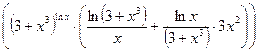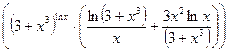
в)

Функция задана в неявной форме. По правилу дифференцирования неявной функции, получим:

г)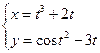

В задачах 71–90 исследовать функцию не непрерывность и построить ее график.

85.

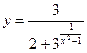
Решение.

Данная функция терпит разрыв в точках x₁=–1 и x₂=1, т.к. при этих значениях знаменатель дроби обращается в нуль. Исследуем характер разрыва в каждой из точек.

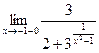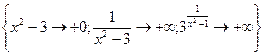= = 0

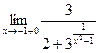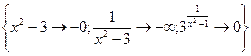= = 1.5

Следовательно, в точке x=–1 функция имеет разрыв первого рода.

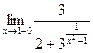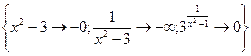= = 1.5

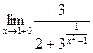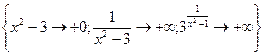= = 0

Следовательно, в точке x=1 функция имеет разрыв первого рода.

Для схематичного построения графика функции найдем поведение функции в бесконечности.

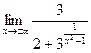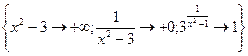= = 1

График.

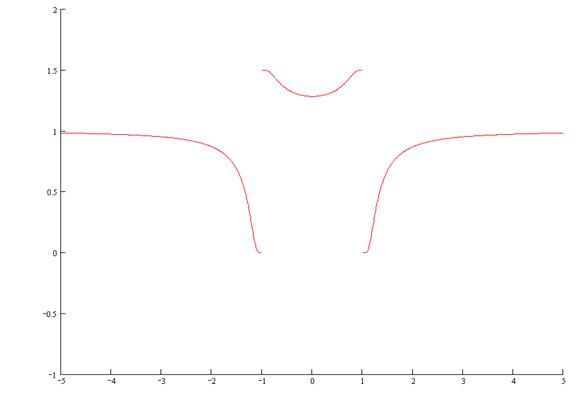
В задачах 91–100 найти наибольшее и наименьшее значение функции y=y(x) на отрезке [a;b].

97. ; a=–3; b=1

Решение.

Наибольшего и наименьшего значения функция может достигать:

1) на концах отрезка, т.е. при x=–3 или при x=1.

2) в критических точках, если они существуют и принадлежат отрезку [–3;1].

Найдем критические точки. Для этого найдем производную функции y’(x)

= =

Производная не существует в точке x=–1

Решим уравнение y’=0

3x²+6x=0

x²+2x=0

x=–2;0

В точке x=–1 функция имеет разрыв. Найдем пределы функции справа и слева, т.е.

= = –∞

= = +∞

Получается, что в точке x=–1 функция имеет разрыв второго рода.

y(–2) =

y(0) =

Найдем значение функции на границах отрезка.

y(–3) =

y(1) =

Максимальное значение на отрезке функция принимает в точке x=–1+0. Оно равно +∞.

Минимальное значение на отрезке функция принимает в точке x=–1–0. Оно равно –∞.

В задачах 101–110 провести полное исследование функции и построить график:

В задачах 111–120 провести полное исследование функции и построить ее график.

112. a=1; b=1; c=19; d=–30; h=1; f=2; g=–15.

Решение.

Разложим дробь на простые дроби.

B=19–A

5A–3(19–A)=30

5A–57+3A=30

8A=87

A=10.875

B=19–10.875=8.125

Получаем следующее разложение:

Получили следующее представление функции.

1. Область определения функции.

Областью определения функции будет вся числовая прямая, за исключением точек, в которых знаменатели дробей обращаются в ноль, т.е. .

2. Функция не является ни четной, ни нечетной, т.к.

Т.к. в состав функции не входят периодические функции, то функция непериодическая.

3. Непрерывность. Т.к. заданная функция является элементарной, то она непрерывна во всей своей области определения. Точки, в которых функция не существует – точки x=3 и x=–5.

Найдем характер разрыва функции в этих точках.

Следовательно, x=–5 – точка разрыва второго рода.

Следовательно, x=3 – точка разрыва второго рода.

4. Асимптоты.

При x=–5 и x=3 функция терпит разрыв второго рода, следовательно, прямые x=–5 и x=3 – вертикальные асимптоты функции.

Найдем наклонные асимптоты.

= = = 1

Получаем наклонную асимптоту y=x+1.

5. Исследуем функцию по производной.

Точки, в которых производная не существует – точки x=3 и x=–5.

Найдем нули производной.

(x²+2x–15)²–10.875(x+5)²–8.125(x–3)²=0

x⁴+4x²+225+4x³–30x²–60x–10.875x²–108.75x–271.875–8.125x²+48.75x–73.125 = 0

x⁴+4x³–45x²–120x–120=0

(x²+2x+a)² = x⁴+4x²+a²+4x³+2ax²+4ax = x⁴+4x³+(2a+4)x²+4ax+a²

(x²+2x+a)² – ((2a+4+45)x²+(4a+120)x+a²+120) = 0

(x²+2x+a)² – ((2a+49)x²+(4a+120)x+a²+120) = 0

= (2a+60)²–(2a+49)(a²+120) = 4a²+240a+3600–2a³–49a²–240a–5880 = –2a³–45a²–2280

–2a³–45a²–2280=0

a³+22.5a²+1140=0

a=b–7.5

(b–7.5)³+22.5(b–7.5)²+1140 = 0

b³–22.5b²+168.75b–421.875+22.5b²–337.5b+1265.625+1140=0

b³–168.75b+1983.75=0

Q=168.75/3 = 56.25

R= 1983.75/2 = 991.875

Т.к. R²≥Q³, то уравнение имеет один действительный корень.

= = = = –12.3629

B= Q/A = 56.25/(–12.3629) = –4.5499

b=–12.3629–4.5499=–16.9128

a=–16.9128–7.5=–24.4128

(x²+2x+a)² – ((2a+49)x²+(4a+120)x+a²+120) = 0

(x²+2x–24.4128)² – ((2∙(–24.4128)+49)x²+(4∙(–24.4128)+120)x+(–24.4128)²+120) = 0

(x²+2x–24.4128)² – (0.1744x²+22.3488x+715.98480384) = 0

(x²+2x–24.4128)² – 0.1744(x²+128.1468x+4105.41745321) = 0

(x²+2x–24.4128)² – 0.1744(x+64.0734)² = 0

(x²+2x–24.4128)² – (0.4176x+26.7571)² = 0

(x²+2x–24.4128+0.4176x+26.7571)(x²+2x–24.4128–0.4176x–26.7571) = 0

x⁴+4x³–45x²–120x–120=0

(x²+2.4176x+2.3443)(x²+1.5824x–51.1699) = 0

x²+2.4176x+2.3443=0

= 1.2088²–2.3443 = –0.8831

Действительных корней нет.

x²+1.5824x–51.1699=0

= 0.7912²+51.1699 = 51.79589744

(–∞;

–7.9881)

–7.9881

(–79881;

–5)

–5

(–5;3)

(3; 6.4057)

6.4057

(6.4057; +∞)

–

Не сущ.

–

Не сущ.

–

↑

макс.

↓

Не сущ.

↓

Не сущ.

↓

мин.

↑

6. Исследуем функцию по второй производной.

Точки, в которых производная не существует – точки x=3 и x=–5.

Найдем нули производной.

21.75(x+5)³+16.25(x–3)³ = 0

87(x+5)³+65(x–3)³ = 0

87(x³+15x²+75x+125)+65(x³–9x²+27x–27) = 0

87x³+1275x²+6625x+10875+65x³–585x²+1755x–1755=0

152x³+690x²+8380x+9120=0

76x³+345x²+4190x+4560=0

x³+4.54x²+55.13x+60=0

Q=(4.54²–3∙55.13)/9 = (20.6116–165.57)/9 = –16.1065

R= (2∙4.54³–9∙4.54∙55.13+27∙60)/54 = (187.153328–2252.6118+1620)/54 = –445.458472/54 = –8.2492

Т.к. R²≥Q³, то уравнение имеет один действительный корень.

= = = 4.1872

B= Q/A = –16.1065/4.1872 = –3.8466

x=4.1872–3.8466–4.54/3=–1.1727

x	(–∞;–5)	–5	(–5;–1.1727)	–1.1727	(–1.1727; 3)	3	(3;+∞)
y"	–	Не сущ.	+	0	–	Не сущ.	+
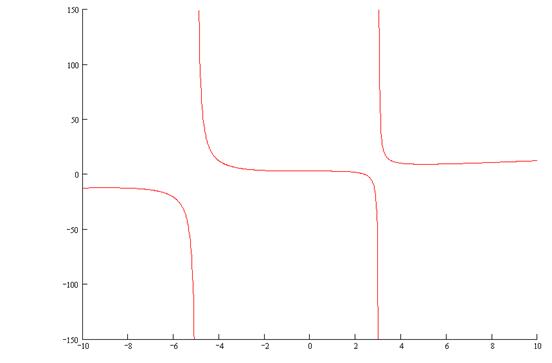
y	Выпукла	Не сущ.	Вогнута	Т. перегиба	Выпукла	Не сущ.	Вогнута

Контрольная работа № 3.

В задачах 121–140 найти и построить область определения функции двух переменных:

121.

Решение.

Функция имеет действительные значения, когда выполнено условие:

–x²≤y≤x²

В задачах 141–160 вычислить указанные частные производные.

160. Найти , , если

Решение.

Функция z – функция сложная, т.к. z=z(u,v), u=u(x,y), v=v(x,y).

= = =

В задачах 161–170 вычислить приближенно следующие значения, используя формулы дифференциального исчисления функции двух переменных:

165.

Решение.

Воспользуемся формулой приближенных вычислений:

Составим функцию , заменив числовые значения переменными. Полагаем x+Δx = 5.02, y+Δy = 1.97, т.е. x=5, Δx=0.02, y=2, Δy=–0.03, тогда f(x;y) = =

Найдем частные производные функции.

= =

Найдем значение производных в точке x=5; y=2.

= = =

Подставим найденные значения в формулу приближенных вычислений:

≈ = 0.335185

177. Найти наибольшее и наименьшее значение функции z=5x²–3xy+y²+4 в области D: {x+y=1; y=–1; x=–1}.

Решение.

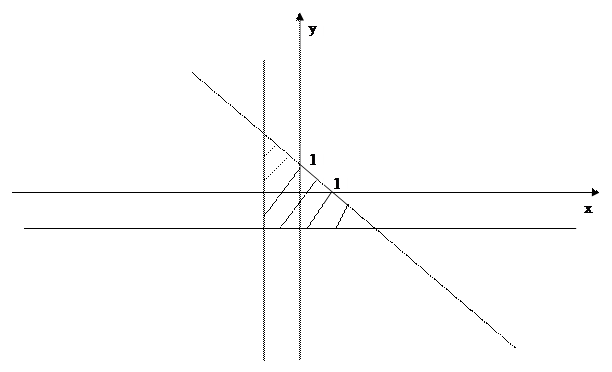
Наибольшего и наименьшего значения функция достигает:

1) в критических точках, если они принадлежат области D;

2) на границах области D;

3) в точках пересечения границ D.

1. Найдем критические точки. Для этого сначала находим:

Координаты критической точки являются решением системы:

y=1.5x

10x–4.5x=0

5.5x=0

x=0

–3y=0

y=0

Точка P₁(0;0) – критическая. Она попадает в область D.

2. Исследуем функцию на границах области D.

Ее границы задаются уравнениями x+y=1; y=–1; x=–1

а) если x=–1, то z = 5+3y+y²+4 = y²+3y+9 – функция одной переменной. Найдем ее критические точки.

z'=2y+3

2y+3=0

y=–1.5

Получаем критическую точку P₂(–1;–1.5), не попадающую в область D.

б) если y=–1, то z=5x²+3x+1 – функция одной переменной. Найдем ее критические точки.

z'=10x+3

10x+3=0

x=–0.3.

Получаем критическую точку P₃(–0.3;–1), попадающую в область D.

в) если x+y=1, то y=1–x и z = 5x²–3x(1–x)+(1–x)²+4 = 5x²–3x+3x²+1–2x+x²+4 = 9x²–5x+5 – функция одной переменной. Найдем ее критические точки.

z'=18x–5.

18x–5=0

Получили критическую точку P₄, попадающую в область D.

3. Угловые точки области P₅(–1;–1), P₆(–1;2), P₇(2;–1).

Таким образом получили 6 точек, в которых функция может достигать наибольшего и наименьшего значения: P₁, P₃, P₄, P₅, P₆, P₇. Вычислим значения функции z в этих точках и выберем из них наибольшее и наименьшее.

Z(0;0)=4

Z(–0.3;–1)=5·(–0.3)²–3·(–0.3)·(–1)+(–1)²+4 = 0.45–0.9+1+4 = 4.55

= = = = ≈ 4.305556