1. Составить математическую модель задачи.

Из двух сортов бензина составляют для различных целей 2 смеси – А и В. Смесь А содержит 60% бензина первого сорта и 40% бензина 2 сорта. Смесь B состоит из 80% бензина первого сорта и 20% бензина 2 сорта Продажная цена 1 кг смеси А – 10 коп., смеси В – 12 коп.

Составить план образования смесей, при котором будет получен максимальный доход, если в наличии имеется 50 т бензина 1 сорта и 30 т бензина второго сорта.

Решение.

Z=10x₁+12x₂→max

0.6x₁+0.8x₂≤50

0.4x₁+0.2x₂≤30

x₁≥0; x₂≥0

2. Графический метод решения задачи линейного программирования. Решить графическим методом следующую задачу линейного программирования с двумя переменными.

Z=3x₁+5x₂→min, max

при условиях:

x₁+x₂≤5

3x₁–x₂≤3

x₁≥0; x₂≥0

Решение.

x1

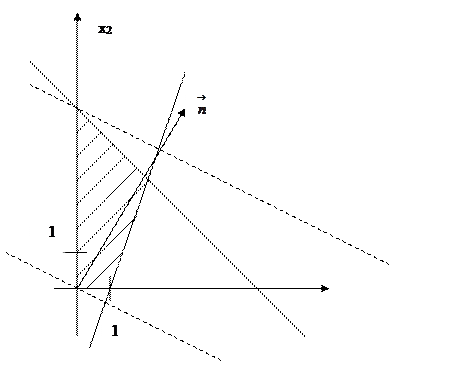
Область допустимых значений образует заштрихованный четырехугольник.

Строим нормаль линий уровня

Построив опорные линии (на чертеже обозначены пунктиром), получаем, что минимум целевой функции достигается в точке (0;0) и равен 0. Максимум целевой функции достигается в точке (0;5) и равен 25.

4. Транспортная задача.

Мощности поставщиков.

A₁=30; A₂=10; A₃=40; A₄=70;

Спрос потребителей.

B₁=60; B₂=10; B₃=20; B₄=10;

Удельные затраты на перевозку.

Строки – поставщики; столбцы – потребители.

	B1	B2	B3	B4
A1	1.2	1.6	1.7	1.5
A2	1.4	1.0	1.2	1.5
A3	1.6	1.4	1.2	1.4
A4	1.5	1.2	1.4	1.2

Решение.

Т.к. задача с неправильным балансом, введем фиктивного потребителя B₅ с запросами, равными 50.

Воспользуемся методом минимальной стоимости. Решение будем искать по следующему принципу: возьмем минимальное значение стоимости перевозок из таблицы. Запишем туда минимальное значение из запасов поставщика или спроса потребителя соответствующей строки или столбца. Если мы распределили все мощности данного поставщика, то вычеркиваем из таблицы соответствующую строку. Если мы распределили весь спрос потребителя, то вычеркиваем из таблицы соответствующий столбец. Продолжаем такие действия до распределения всех запасов по потребителям.

Используя метод минимальной стоимости, получим следующее решение:

	B1	B2	B3	B4	B5
A1	30	0	0	0	0
A2	0	10	0	0	0
A3	0	0	20	0	20
A4	30	0	0	10	30

5. Универсальный метод транспортной задачи.

Для расчета мощности i-го вида транспорта необходимо воспользоваться значениями: S=2 смены; Z=8 часов; d=25 дней; P₁=10т, P₂=5т, P₃=10т, P₄=15т.

Численность транспорта (i)

n₁=20; n₂=30;n₃=30;n₄=20.

Спрос потребителей (j):

B₁=120; B₂=70; B₃=50; B₄=120.

В таблице первое значение – c – себестоимость перевозки j-го груза i-м видом транспорта (руб/маш·ч), второе – t время на транспортировку i-го продукта j-м видом транспорта (ч).

	B1	B2	B3	B4
n1	3;3	4;4	5;2.5	6;4
n2	5;5	6;6	7;5	4;4
n3	2;2	3;3	4;4	3;4
n4	5;4	4;3	2;3	2;4

Решение.

Рассчитаем мощность транспортных средств по формуле.

A_i=d·Z·S·n_i

Получим:

A₁ = 25·8·2·20 = 8000

A₂ = 25·8·2·30 = 12000

A₃ = 25·8·2·30 = 12000

A₄ = 25·8·2·20 = 8000

6. Игровые задачи.

Для обслуживания потребителей предприятие может выделить три вида транспорта А₁, А₂ и А₃, получая прибыль, зависящую от спроса на них. В матрице элементы α_ij, характеризуют прибыль, которую предприятие получает при использовании транспорта A_i и состоянии спроса B_j.

	B1	B2	B3	B4
A1	7	5	0	5
A2	3	4	5	7
A3	4	5	6	7

Определите оптимальную пропорцию транспортных средств (считая, что доля транспортных средств характеризуется вероятностью использования i-го вида транспорта), предполагая при этом, что состояние спроса является полностью неопределенным. Прибыль должна гарантироваться при любом состоянии спроса.

С этой целью необходимо представить задачу как матричную игру двух лиц (предприятие – спрос) с нулевой суммой, исключить заведомо невыгодные стратегии игроков (упростить задачу), найти оптимальные стратегии и цену игры сведением игры к паре симметричных двойственных задач линейного программирования, определить оптимальную структуру транспортных средств.

Решение.

Составим двойственную пару задач линейного программирования.

Для первого игрока (спрос)

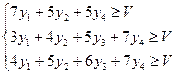
y₁+y₂+y₃+y₄=1

Освобождаясь от переменной V (цена игры), разделим левую и правую часть выражений на V. Приняв y_i/V за новую переменную z_i получим новую систему ограничений и целевую функцию.

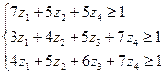
Для второго игрока (предприятие)

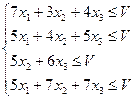
x₁+x₂+x₃=1

Освобождаясь от переменной V (цена игры), разделим левую и правую часть выражений на V. Приняв x_i/V за новую переменную d_i получим новую систему ограничений и целевую функцию.

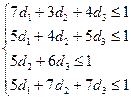
Приведем модель к канонической форме.

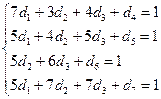
Построим симплекс-таблицу

Б.п.	1	–d1	–d2	–d3
d4	1	7	3	4
d5	1	5	4	5
d6	1	0	5	6
d7	1	4	7	7
ψ	0	–1	–1	–1

Опорный план (0;0;0;1;1;1;1)

Ключевой столбец – d₃

Ключевая строка – d₇

Получаем новую симплекс-таблицу.

Б.п.	1	–d1	–d2	–d7
d4	3/7	33/7	–1	–4/7
d5	2/7	15/7	–1	–5/7
d6	1/7	–24/7	–1	–6/7
d3	1/7	4/7	1	1/7
ψ	8/7	–3/7	0	1/7

Опорный план (0;0;8/7;3/7;2/7;2/7;0)

Ключевой столбец – d₁

Ключевая строка – d₄

Получаем новую симплекс-таблицу.

Б.п.	1	–d4	–d2	–d7
d1	1/11	7/33	–7/33	–4/33
d5	3/7	–5/11	–18/7	–15/7
d6	15/7	8/11	–57/7	–102/49
d3	3/7	–4/33	37/7	1
ψ	39/7	1/11	–3/7	3/7

Опорный план (1/11;0;39/7;0;3/7;15/7;0)

Ключевой столбец – d₂

Ключевая строка – d₃

Получаем новую симплекс-таблицу.

Б.п.	1	–d4	–d3	–d7
d1	4/7	65/33	49/1221	–3/7
d5	495/49	–483/231	18/37	–429/49
d6	726/49	224/77	57/37	–102/49
d2	1/9	–28/1221	7/37	7/37
ψ	1447/39	132/231	3/37	132/49

Опорный план (4/7;1/8;0;0;495/49;726/49;0)

Получаем оптимальное решение:

d₁ = 4/7

d₂ = 1/8

d₃ = 0

Цена игры V =

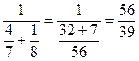
Исходные параметры, относительные частоты применения стратегий.

x₁ =

x₂ =

x₃ = 0

7. Задачи на экстремум.

На плоскости x₁x₂ построить допустимую область, определяемую заданной системой ограничений. Найти в этой области оптимальные решения задач максимизации и минимизации целевой функции Z.

Z=(x₁–2)²+(x₂–3)²

x₁²–8x₂–8≥0

5x₁–4x₂–28≤0

x₁≥0; x₂≤3

Решение.

Строим область, соответствующую системе ограничений задачи. На чертеже это заштрихованная область.

Из чертежа видно, что минимум целевой функции будет лежать на границе области ограничений.

Для определения координат точки минимума воспользуемся равенством

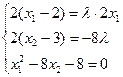
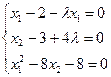
λ=0.75–0.25x₂

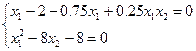
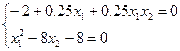
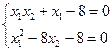
x₂=0.125x₁²–1

0.125x₁³–x₁+x₁–8=0

0.125x₁³–8=0

x₁³–64=0

x₁=4

x₂=1

λ=0.5

Следовательно, минимум функции достигается в точке (4;1) и равен (4–2)²+(1–3)² = 4+4 = 8.

Максимум целевой функции, как видно из рисунка, будет достигаться в точке (0;–7) и будет равен (0–2)²+(–7–3)² = 4+100 = 104.

9. Планирование капитальных вложений.

Интервал планирования Т=5 лет. Функция затрат на ремент и дальнейшую эксплуатацию: K(τ)=τ+0.5τ² (руб.). Функция замены: P(τ)=6+0.05τ² (руб.) определить оптимальную стратегию замены и ремонта для нового оборудования (τ=0) и оборудования возраста τ=1; τ=2; τ=3.

Определить оптимальные планируемые затраты по годам пятилетки, если количество оборудования по возрастным группам следующее: n(τ=0)=10; n(τ=1)=12; n(τ=2)=8; n(τ=3)=5.

11. Эффективность сферы реальных услуг.

Автомашина при ее эксплуатации может находиться в следующих состояниях:

X₀ – исправна;

X₁ – неисправна, проходит осмотр, который проводится с целью определения типа ремонта;

X₂ – неисправна, проходит капитальный ремонт;

X₃ – неисправна, проходит средний ремонт;

X₄ – неисправна, проходит текущий ремонт;

X₅ – отремонтирована, проходит контроль и испытание на определение качества ремонта и выявление дефектов.

Среднее время межремонтного пробега равно t₀ = 0.5 лет. Среднее время осмотра машины – t₁ = 4 года. Вероятность q_i каждого вида ремонта устанавливается исходя из уровня учета полного набора событий на интервале межкапитального ремонта в виде отношения количества ремонтов K_i каждого вида по всему количеству ремонтов в этом интервале, т.е.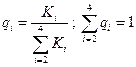

Длительность межкапитального интервала – t_k = 6 лет, среднего t_c = 2 года, текущего – t_т = 0.5 лет.

После ремонта машина поступает на послеремонтный контроль. Качество ремонта определяется вероятностью 0.9 для капитального ремонта, 0.6 – среднего и 0.9 – текущего.

Изобразить график состояний системы с интенсивностями проходов из состояния в состояние. Определить вероятность нахождения машины в каждом из состояний, включая исправное состояние машины P₀, а так же среднее время простоя машины

Решение.

Граф состояний машины представлен ниже.

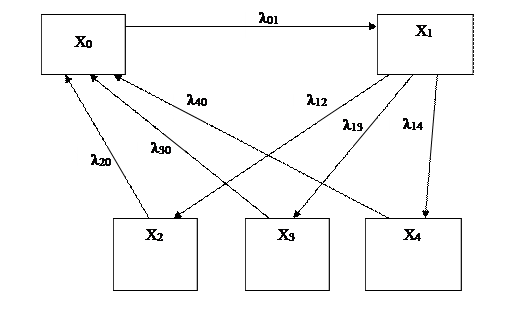
Найдем q_i. Возьмем период времени 6 лет. За это время будет проведен 1 капитальный ремонт, 3 средних ремонта и 12 текущих ремонтов, т.е. K₂=1; K₃=3; K₄=12.

q₂ = 1/16 = 0.0625; q₃ = 3/16 = 0.1875; q₄ = 12/16 = 0.75;

Найдем интенсивности потоков, переводящих автомашину из состояния в состояние:

Считая, что все потоки простейшие с вышеуказанными интенсивностями, найдем вероятность каждого состояния. Решим соответствующую систему однородных алгебраических уравнений.

0=–λ₀₁P₀+λ₂₀P₂+λ₃₀P₃+ λ₄₀P₄

0=– λ₂₀P₂–λ₁₂P₁

0=– λ₃₀P₃+λ₁₃P₁

0=– λ₄₀P₄+λ₁₄P₁

Решение этой системы, удовлетворяющее нормировочному условию  имеет вид:

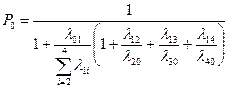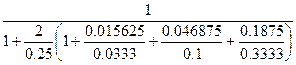 =  =  =  =  = 0.047619

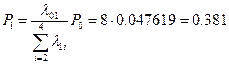
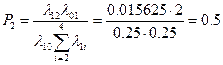
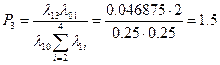
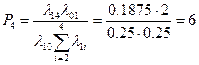
Среднее время простоя машины равно

13. Определение оптимального размера автопарка.

Средняя скорость поступления пакетов на базу –  = 1200.

Стандартное отклонение поступления –  = 100.

Средний объем вывоза на машину – D_i – 120.

Стандартное отклонение на машину – ΔD_i – 10.

Затраты на эксплуатацию автомобиля в день – c = 10.

Стоимость сверхурочного времени работы – q – 25.

Определить наиболее эффективную структуру парка машин.

Примечание. Воспользоваться выборкой из пяти случайных нормальных чисел α=(0.464; 0.060; 1.486; 1.022; 1.394) β=(0.137; –2.526; –0.354; –0.472; –0.555)

Решение.

Расчетные выражения задачи.

1. Общее число поступающих пакетов, подлежащих доставке в i-й день,

,

где - среднесуточное поступление, - стандартное отклонение от B_i, α_i – табличное значение нормального распределения, i=1…5 – выборка пяти рабочих дней в неделю.

2. Общее число пакетов, подлежащих доставке с учетом остатка предыдущего дня.

В_i=B+d_i-1,

где d_i-1 – остаток пакетов, не вывезенных с предыдущего дня.

3. Общее количество пакетов, которое может быть доставлено в течение рабочего дня.

где n – количество машин, - среднее количество пакетов на одну машину в день, - стандартное отклонение от ,  - табличное значение нормального распределения.

4. Число пакетов, оставшихся для обработки при отсутствии сверхурочного времени.

d_i=B_i­­–D_i

5. Число пакетов, подлежащих отправке в сверхурочное время

6. Стоимость сверхурочной доставки в предположении, что скорость обслуживания остается неизменной.

где - длительность рабочего дня (8 ч), С – стоимость сверхурочной часовой работы (8 руб./ч)

Результаты расчета сведем в таблицу (см. ниже).

7. Общие затраты по автопарку, включая обслуживание машин,

где q – стоимость обслуживания машин в сутки, d – количество рабочих дней в неделю.

Результаты расчетов представим в таблице.

Кол-во машин, дни	Число пакетов, подлежащих отправке	Число пакетов, которое может быть отправлено	Кол-во неотпр. пакетов	Кол-во пакетов, сверхур. отправл.	Издержки на сверхур. время
n	ti	αi	Bi	Bi	βi	Di	di	Di*	Qi
15	1	0.464	1246	1246	0.137	1521	0	0	0
2	0.060	1206	931	-2.526	1121	0	85	227
3	1.486	1349	1159	-0.354	1447	0	0	0
4	1.022	1302	1014	-0.472	1429	0	0	0
5	1.394	1339	924	-0.555	1417	0	0	0
Q = 227+15·10·5 = 977
16	1	0.464	1246	1246	0.137	1622	0	0	0
2	0.060	1206	830	-2.526	1196	0	10	27
3	1.486	1349	983	-0.354	1543	0	0	0
4	1.022	1302	742	-0.472	1524	0	0	0
5	1.394	1339	557	-0.555	1511	0	0	0
Q = 27+16·10·5 = 827
17	1	0.464	1246	1246	0.137	1723	0	0	0
2	0.060	1206	729	-2.526	1271	0	0	0
3	1.486	1349	807	-0.354	1640	0	0	0
4	1.022	1302	469	-0.472	1620	0	0	0
5	1.394	1339	188	-0.555	1606	0	0	0
Q = 0+17·10·5 = 850

Получается, что оптимальный размер автопарка равен 16 машин.